3 Calculs de la luminance TOA et de la réflectance TOA
L’étalonnage des capteurs se traduit généralement par une simple conversion linéaire (ou presque) entre la luminance à laquelle le capteur est exposé et la tension créée par les éléments de détection. Cela signifie que si nous enregistrons la tension créée par chaque élément de détection, ainsi que l’emplacement sur la surface de la Terre d’où provient le rayonnement qui a créé le courant, et que nous disposons toutes les tensions mesurées par chacun des éléments de détection dans un schéma spatial en fonction de leur emplacement sur la surface de la Terre, nous pouvons créer une image cartographique dans laquelle les valeurs de chaque pixel sont les tensions mesurées dans cette zone. C’est essentiellement de cette manière que sont créées les images satellites.
Quantification
Cependant, les nombres numériques que nous voyons lorsque nous chargeons une image satellite dans un logiciel ne correspondent pas aux tensions mesurées. Il y a deux raisons liées à cela : réduire la quantité de mémoire informatique nécessaire pour stocker les mesures, tout en fournissant des données avec une précision adéquate. Les tensions mesurées prennent la forme de nombres décimaux, comme 3,560194 mV, qui nécessitent par défaut 32 bits de mémoire informatique pour être stockés (ou 64 bits si un grand nombre de décimales est nécessaire). Mais en réalité, les mesures de tension dans les capteurs des satellites ne sont pas précises à six décimales (comme dans l’exemple ci-dessus) ou à un autre grand nombre de décimales, et il n’est donc pas nécessaire d’utiliser 32 bits de mémoire pour stocker la tension de chaque élément de détection. Ce qui est généralement fait à la place, c’est que pendant, ou même avant, le développement du capteur, la précision nécessaire des mesures est déterminée, et l’instrument est construit pour effectuer des mesures avec cette précision (qui est ensuite testée plus tard lors de l’étalonnage de l’instrument). Une fois que la précision des mesures connut, et en ajoutant des informations sur la gamme de rayonnements/tensions à laquelle l’instrument doit être sensible, le nombre de bits nécessaires pour contenir les mesures peut alors être déterminé, et la tension peut être convertie en un nombre numérique qui peut être stocké comme un nombre entier, ce qui nécessite beaucoup moins de mémoire informatique pour le stockage.
Imaginons, par exemple, que vous souhaitiez mesurer la taille d’une personne et que vous vouliez la mesurer au cm près. En utilisant les centimètres et sachant que tous les adultes mesurés dans l’histoire de ces mesures mesuraient entre 54 cm et 272 cm, vous réalisez que vous n’avez besoin que d’être capable de mesurer 219 valeurs différentes (les deux extrêmes inclus) : 54 cm, 55 cm, 56 cm….. 272 cm. Pour stocker 219 valeurs différentes, vous n’auriez besoin que de 8 bits, car 28 = 256, ce qui vous laisse même quelques valeurs supplémentaires dont vous n’avez pas besoin. Vous décidez alors de coder une taille de 54 cm avec la valeur « 0 », 55 cm avec la valeur « 1 », et ainsi de suite (les valeurs du code sont simplement 54 de moins que les hauteurs correspondantes en cm). Maintenant, lorsque vous mesurez quelqu’un (avec votre mètre ruban très précis) et que vous estimez qu’il mesure 173,234 cm, vous vous dites que vous n’avez besoin que d’une précision en cm, vous arrondissez donc à 173 cm et vous codez 173 – 54 = « 119 ». C’est l’équivalent du nombre numérique que vous voyez dans un pixel d’une bande donnée d’une image. Lorsque vous savez comment le code (« 119 ») se rapporte à la mesure réelle (173 cm), la valeur prend tout son sens. Ce processus de codage est appelé quantification.
Numéros numériques à la luminance TOA
Lorsque vous ouvrez une image satellite dans un logiciel, la valeur initiale que vous voyez dans chaque pixel est appelée un numéro numérique (en anglais « Digital Number », DN), qui est équivalent au code (« 119 ») dans l’exemple ci-dessus. Bien que les DN soient suffisants pour produire une belle visualisation de l’image, si vous voulez traiter l’image comme une série de mesures radiométriques, vous devez la convertir en une quantité physique (comme les 173 cm correspondant à la taille de la personne mesurée dans cet exemple). En télédétection, la traduction d’une valeur de nombre numérique en une mesure de luminance est vraiment un processus en deux étapes. Dans la télédétection optique passive, l’étalonnage du capteur a permis d’établir une relation connue entre la luminance à laquelle le capteur est exposé et la tension générée par le rayonnement, et la quantification a ensuite été utilisée pour coder la tension mesurée sous forme de nombre numérique. Pour convertir ce nombre numérique (DN) en luminance, il faut donc en théorie d’abord une conversion en tension, puis une conversion en luminance. Heureusement, il est facile d’effectuer ces deux conversions en même temps. Nous allons voir comment cela est fait pour les données Landsat à titre d’exemple, mais le même principe s’applique aux données de tous les autres capteurs optiques passifs des satellites.
Les métadonnées Landsat contiennent des coefficients d’étalonnage radiométrique (Figure 20) qui vous permettent de convertir directement les valeurs DN en luminance au sommet de l’atmosphère (TOA). Ces coefficients contiennent un terme de » multiplication » et un terme d' » addition « , chacun étant unique à chaque bande, et ils sont utilisés comme suit : Lλ=multλ*DN+addλ,où L est la luminance et λ, la notation commune pour la longueur d’onde, indique une bande donnée.

Figure 20: Coefficients de calibrage utilisés pour convertir les valeurs DN en valeurs de luminance TOA pour Landsat 8. Par Anders Knudby, CC BY 4.0.
Afin de produire une couche de données matricielles dans laquelle chaque valeur de cellule est une mesure de la luminance TOA, vous pouvez donc utiliser la « Calculatrice matricielle » offert dans tous les logiciels de SIG/télédétection. Certains logiciels disposent même d’outils dédiés à la « calibration radiométrique Landsat » qui trouvent les informations pertinentes dans les métadonnées et les appliquent pour vous.
Numéros numériques à la réflectance TOA
La conversion des valeurs DN en une mesure de la luminance est une étape importante vers l’utilisation des données de télédétection d’une manière quantitative — dans laquelle les valeurs de chaque cellule ont une signification physique réelle. Cependant, il y a un problème principal avec les mesures de luminance : la luminance provenant d’une zone dépend à la fois des caractéristiques physiques de cette zone, comme ce qui se trouve à la surface, mais elle dépend également de la quantité de rayonnement incident sur cette zone. Il est facile de le confirmer par une simple expérience : approchez un interrupteur près de vous, assurez-vous qu’il est allumé et fixez votre regard sur un mur. Notez sa luminosité (une approximation humaine de la quantité de rayonnement qui en émane). Éteignez maintenant la lumière et notez si le mur est devenu plus sombre ou plus clair. Il est devenu plus sombre, bien sûr, ce qui signifie qu’il y a maintenant moins de rayonnement qui en émane. Et cela se produit alors que le mur lui-même n’a pas changé du tout ! Dans le contexte de la télédétection, les mesures de luminance sont donc rarement utilisées directement, mais sont typiquement utilisées comme une étape vers une quantité radiométrique qui est plus étroitement liée à la surface d’où ilv vient : la réflectance. Pour un rayonnement isotrope, la réflectance (R) d’une surface donnée est le rapport entre la luminance sortante et la luminance entrante, également souvent exprimée sur la base de l’exitance (E) et de l’irradiance (I) :
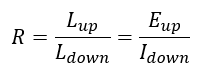
Dans l’exemple du mur, lorsque vous éteignez la lumière, la luminance entrante et sortante est réduite, et la réflectance du mur reste inchangée. Cela s’explique par le fait que la réflectance est une propriété physique du mur qui est indépendante de l’éclairage. Cela en fait un outil idéal pour la télédétection, car il est possible de comparer plusieurs observations avec des éclairements différents, pour des utilisations telles que le suivi de l’évolution d’une zone dans le temps ou la comparaison de différentes zones sur la Terre.
Si nous convertissons les valeurs de luminance du TOA en valeurs de réflectance, nous obtenons ce que l’on appelle la réflectance du TOA, qui est la réflectance de l’ensemble du système Terre-Atmosphère. Pour comprendre ce que cela signifie, imaginez que vous êtes un astronaute et que vous placez un hula hoop de façon horizontale juste au niveau du sommet de l’atmosphère (si le sommet de l’atmosphère était possible à définir et à trouver !), et que vous mesurez ensuite la quantité de rayonnement passant à travers l’anneau dans les orientations ascendantes et descendantes. En divisant l’un par l’autre, on obtient la réflectance TOA.
Le calcul de la réflectance TOA s’effectue un peu différemment selon le type de données. Pour Landsat 8, il existe un autre ensemble de coefficients de calibration que vous pouvez appliquer exactement comme vous pouvez appliquer ceux de la luminance TOA (Figure 21).

Figure 21: Coefficients de calibrage utilisés pour convertir les valeurs DN en valeurs de réflectance TOA pour Landsat 8. Notez que les valeurs pour les bandes 10 et 11 ne sont pas fournies, car ces bandes ne mesurent pas le rayonnement solaire réfléchi (sauf à un degré négligeable). Notez également que les coefficients sont les mêmes pour toutes les bandes – pour Landsat 8, les valeurs DN ont été générées spécifiquement pour chaque scène afin de garantir des coefficients de calibration de réflectance TOA constants. Par Anders Knudby, CC BY 4.0.
Pour les anciennes données Landsat, ainsi que pour plusieurs autres types de capteurs, il est nécessaire de calculer explicitement la quantité de rayonnement solaire entrant au sommet de l’atmosphère, et de diviser la luminance par cette valeur tout en corrigeant la différence entre luminance et irradiance et l’angle du rayonnement solaire entrant. Cela se fait de manière générique avec l’équation suivante (réarrangée pour des raisons pédagogiques à partir de l’équation 4, page 79, du manuel Landsat 7), expliquée plus en détail ci-dessous :
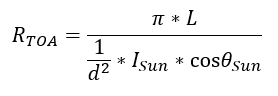
où RTOA est la réflectance au sommet de l’atmosphère, L est la luminance (vers le haut), d est la distance Terre-Soleil en unités astronomiques, ISun est l’irradiance solaire extraterrestre moyenne, et θSun est l’angle zénithal solaire – l’angle entre la direction vers le Soleil et la normale à la surface de la Terre. L’équation est une division entre le rayonnement sortant dans toutes les directions vers le haut (c’est-à-dire l’exitance, au numérateur) et le rayonnement entrant dans toutes les directions vers le bas (c’est-à-dire l’irradiance, au dénominateur).
Le numérateur est relativement simple : la luminance ascendante, L, qui est quantifiée comme le rayonnement par unité de surface exposée se déplaçant dans des directions comprises dans un angle solide spécifié, est multipliée par π pour la convertir en une valeur qui quantifie plutôt le rayonnement se déplaçant dans toutes les directions ascendantes, afin de la rendre comparable à l’irradiance solaire entrante au dénominateur.
l’irradiation solaire moyenne entrante au sommet de l’atmosphère. Comme la distance entre le Soleil et la Terre varie tout au long de l’année et que la quantité d’irradiation solaire varie avec elle, nous devons corriger cette valeur par le facteur 1/d2, où d est la distance réelle entre le Soleil et la Terre au moment de l’acquisition de l’image. Si le Soleil était au zénith (directement au-dessus de la Terre), cela permettrait de quantifier l’irradiance entrante par unité de surface. Dans le cas où le Soleil n’est pas au zénith, il faut multiplier cette valeur par le cosinus de l’angle zénithal solaire pour obtenir l’éclairement énergétique par unité de surface exposée.
Note: Dans les deux équations ci-dessus, l’indice λ indiquant que ces calculs doivent être effectués bande par bande a été omis pour plus de clarté, mais gardez cela à l’esprit. L varie d’une bande à l’autre, tout comme l’ISun, de sorte que les deux doivent être calculés spécifiquement pour chaque bande afin d’être corrects.
Grâce à ces calculs, vous êtes en mesure de convertir les valeurs DN de chaque pixel en une mesure de la réflectance TOA, qui est une propriété physique du système Terre-Atmosphère. Le fait que la réflectance TOA ne soit pas un nombre arbitraire dépendant de l’étalonnage du capteur et de l’éclairage, mais plutôt une propriété physique des parties de la Terre visibles sur l’image, nous permet d’utiliser des images capturées par différents capteurs, à différents moments et pour différentes zones, et de comparer directement les valeurs de chaque pixel. Le seul problème qui subsiste dans cette approche est que la plupart des chercheurs sont plus intéressés par la réflectance de la surface de la Terre que par la réflectance au sommet de l’atmosphère, mais l’état de l’atmosphère et l’état de la surface influencent tous deux la réflectance TOA. L’étape suivante du traitement des données de chaque pixel consiste donc à supprimer l’influence de l’atmosphère sur ces valeurs, pour arriver à une mesure de la réflectance de la surface !

