10 Photogrammétrie et Structure-from-Motion

Toutes les applications des données de télédétection couvertes dans les chapitres précédents ont été basées soit sur des images individuelles (par exemple, la classification), soit sur des séries temporelles d’images (par exemple, la détection de changements). Cependant, lorsque deux images (ou plus) de la même zone sont acquises, en succession rapide et sous différents angles, il est possible d’extraire des informations géométriques sur la zone cartographiée, tout comme nos yeux et notre cerveau extraient des informations 3D sur le monde qui nous entoure lorsque nous le regardons avec nos deux yeux. C’est le sous-domaine de la télédétection appelé photogrammétrie.

Photogrammétrie traditionnelle (image unique et stéréo)

La photogrammétrie consiste à utiliser des informations sur la géométrie de l’image (distance entre le capteur et l’objet, position et orientation du capteur, et géométrie interne du capteur) pour en déduire des informations sur la position, la forme et la taille des objets vus sur l’image. La photogrammétrie est utilisée depuis les premières utilisations de la photographie aérienne, et l’idée de base dans ce domaine est de permettre la mesure des distances dans l’image. Ainsi, la photogrammétrie vous permet de déterminer la longueur d’un segment de route, la distance entre un point A et un point B et la taille réelle de votre patinoire locale (en supposant que vous en ayez une image bien calibrée). Vous pouvez imaginer que vous prenez une photographie aérienne et que vous la manipulez de manière à pouvoir la superposer dans une SIG ou sur Google Earth. Une fois les coordonnées géographiques associées à l’image, la mesure des distances devient possible.

Image verticale unique, terrain plat

Le scénario le plus simple possible en photogrammétrie est que vous avez une image produite par un capteur pointant directement vers la Terre, et que l’image contient un terrain parfaitement plat. Si nous supposons que l’image a été prise par un capteur situé soit sur un avion volant à très haute altitude, soit sur un satellite, et que l’image ne couvre qu’une très petite zone, nous pouvons faire l’hypothèse réductrice que chaque partie de l’image a été imagée exactement depuis le zénith, comme ceci, et que par conséquent la distance entre le capteur et la surface de la Terre est la même sur toute l’image (Figure 75).

Dans ce cas, l’échelle de l’image est égale au rapport entre la distance focale de la caméra (f, ou une mesure équivalente pour les types de capteurs autres que les caméras à sténopé) et la distance entre le capteur et le sol (H) :

Échelle = f / H

Si vous connaissez l’échelle de votre image, vous pouvez alors mesurer les distances entre les objets du monde réel en mesurant leur distance dans l’image et en divisant par l’échelle (notez que l’échelle est une fraction dont le numérateur est 1, donc diviser par l’échelle revient à multiplier par le dénominateur).

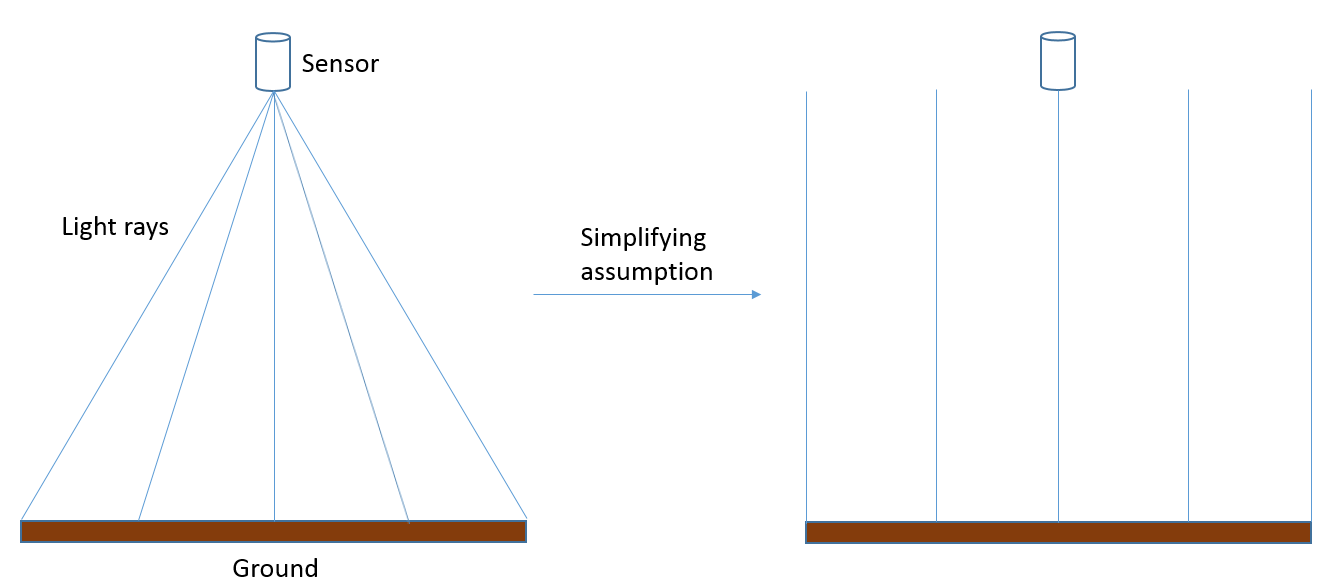
Figure 75: En réalité, une image est créée à partir de la lumière qui atteint le capteur à différents angles depuis différentes parties de la surface de la Terre. Pour les besoins actuels, nous pouvons supposer que ces angles ne sont en fait pas différents et que, par conséquent, la distance entre le capteur et la surface de la Terre est la même sur toute l’image. En réalité, cette hypothèse n’est pas correcte, et l’échelle/résolution spatiale change en fait du centre de l’image vers les bords de l’image. Anders Knudby, CC BY 4.0.

Cette définition de l’échelle n’est vraiment pertinente que pour la photographie aérienne analogique, où l’image est imprimée sur papier et où la relation entre la longueur des éléments de l’image et la longueur de ces mêmes éléments dans le monde réel est fixe. Pour la photographie aérienne numérique, ou lorsque l’imagerie satellitaire est utilisée en photogrammétrie, l’ « échelle » de l’image dépend du niveau de zoom, que l’utilisateur peut faire varier, de sorte que la mesure la plus pertinente du détail spatial est la résolution spatiale que nous avons déjà examinée dans les chapitres précédents. La résolution spatiale est définie comme la longueur sur le terrain d’un côté d’un pixel, et elle ne change pas en fonction du niveau de zoom (ce qui change lorsque vous faites un zoom avant ou arrière est simplement le grain avec lequel l’image apparaît sur votre écran). Nous pouvons toutefois définir une résolution spatiale « native » d’une manière similaire à celle utilisée pour l’imagerie analogique, en nous basant sur la distance focale (f), la taille des éléments de détection individuels sur le capteur de la caméra (d) et la distance entre le capteur et le sol (H) :

Résolution = (f*d) / H

Image verticale unique, terrain vallonné

La situation se complique lorsqu’une image est prise sur un terrain qui ne peut raisonnablement pas être considéré comme parfaitement plat, ou lorsque la distance entre le capteur et le sol est suffisamment petite, ou la zone couverte par l’image suffisamment grande, pour que la distance réelle entre le capteur et le sol change sensiblement entre les différentes parties de l’image :

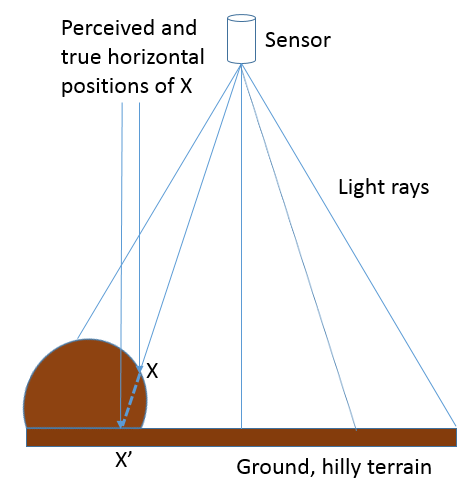
Figure 76: Lorsqu’une image est prise plus près de la surface de la Terre, ou sur un terrain plus accidenté, la distance entre le capteur et la surface de la Terre ne peut pas être considérée comme constante sur toute l’image. Si l’on n’en tient pas compte, cela entraîne un déplacement vertical et horizontal des objets imagés. Anders Knudby, CC BY 4.0.

Les terrains accidentés posent un certain nombre de problèmes en photogrammétrie, le plus important étant le déplacement vertical et horizontal des objets imagés. Comme l’illustre la figure 76, si l’on suppose que le point X se trouve sur la surface plane (et non sur la colline où il se trouve réellement), sa position horizontale sera censée se situer en X », car c’est là que le « rayon lumineux » coupe le sol plat. En réalité, bien sûr, sa position horizontale n’est pas à X ». Si le terrain de la zone imagée est connu, par exemple grâce à un modèle numérique d’élévation de haute qualité, il peut être pris en compte lors du géoréférencement de l’image et l’intersection correcte entre le « rayon lumineux » et le sol (sur la colline) peut être identifiée. En revanche, s’il n’existe pas de modèle numérique d’élévation, l’effet du terrain — connu sous le nom de déplacement du relief — ne peut pas être explicitement pris en compte, même s’il est évident dans l’imagerie résultante.

Imagerie stéréo

Jusqu’à il y a dix ans, l’utilisation la plus avancée de la photogrammétrie consistait probablement à utiliser un couple stéréoscopique (deux images couvrant la même zone à partir de points de vue différents) pour dériver directement un modèle numérique d’élévation à partir de l’imagerie, ce qui permettait également de mesurer la hauteur d’objets tels que des bâtiments, des arbres, des voitures, etc. Le principe de base de la stéréoscopie, comme on appelle cette technique, est la reproduction de ce que vous faites tout le temps avec vos deux yeux : en observant un objet ou un paysage sous deux angles différents, il est possible d’en reconstruire un modèle tridimensionnel. Bien qu’il existe un art sophistiqué pour réaliser cette technique avec une grande précision (un art que nous ne pouvons pas explorer dans le cadre de ce cours), nous allons passer en revue l’idée de base ici.

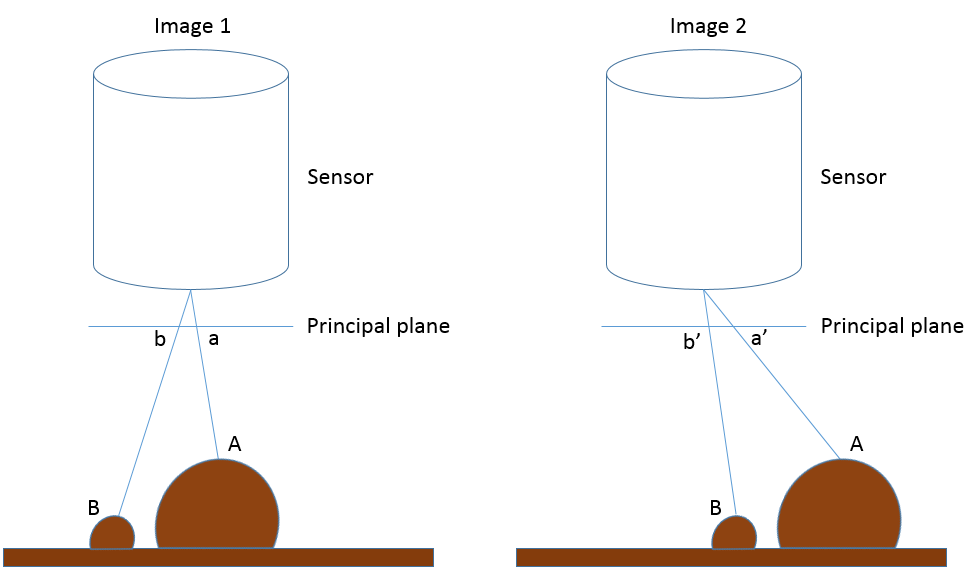
Figure 77: Illustration de la façon dont les positions horizontales apparentes des points A et B changent entre les deux images qui forment une vue stéréo de la zone. La taille du capteur a été fortement exagérée pour montrer l’emplacement de chaque point sur le plan principal. Anders Knudby, CC BY 4.0.

Dans la figure 77, l’image 1 et l’image 2 représentent une vue stéréo du paysage qui contient un terrain plat et deux collines, avec les points A et B. Sur le côté gauche de la figure (image 1), a et b indiquent les emplacements de chaque point sur le plan principal de cette image, ce qui correspond à l’emplacement des points dans l’image résultante. Sur le côté droit de la figure, la caméra s’est déplacée vers la gauche (en suivant la trajectoire de vol de l’avion ou le mouvement du satellite sur son orbite), et là encore, b’ et a’ désignent les emplacements où chaque point serait enregistré sur le plan principal de cette image. Il est important de noter qu’a est différent de a’ parce que le capteur s’est déplacé entre les deux images, et de la même manière, b est différent de b ». Plus précisément, comme l’illustre la figure 78, la distance entre a et a’ est plus grande que la distance entre b et b », parce que A est plus proche du capteur que B. Ces distances, connues sous le nom de parallaxe, sont celles qui transmettent l’information sur la distance entre le capteur et chaque point, et donc sur l’altitude à laquelle chaque point est situé. Pour calculer la hauteur de A par rapport au niveau du sol plat, au niveau relatif de la mer ou à une référence verticale, ou encore mieux, pour obtenir un modèle numérique d’élévation de toute la zone, il faut positionner soigneusement les deux images (généralement en localisant de nombreux éléments de surface pouvant être reconnus sur les deux images), connaître la position et l’orientation du capteur au moment de l’acquisition des deux images (généralement à l’aide d’informations basées sur le GPS), et enfin connaître la géométrie interne du capteur (généralement, ces informations sont fournies par le fabricant du capteur).

Figure 78: Mouvement de a à a’, et de b à b’, entre l’image 1 et l’image 2 de la figure 77. Anders Knudby, CC BY 4.0.

Les mathématiques appliquées à la stéréoscopie sont assez compliquées, mais en pratique, même un novice peut produire des modèles numériques d’élévation utiles à partir d’images stéréoscopiques avec un logiciel commercial. Bien qu’il existe des logiciels spécialisés en photogrammétrie, les grands progiciels commerciaux de télédétection comprennent généralement un » module de photogrammétrie » qui peut vous aider à produire des modèles numériques d’élévation, même si vous n’êtes pas un expert en photogrammétrie. Dans ce qui précède, nous avons supposé que l’imagerie était orientée au nadir (c’est-à-dire que le capteur était pointé directement vers la Terre pour chaque image), car les concepts deviennent plus compliqués lorsque ce n’est pas le cas, mais des solutions mathématiques existent également pour l’imagerie oblique. En fait, l’un des attributs utiles de plusieurs satellites modernes équipés de capteurs d’images est leur capacité à s’incliner, ce qui permet à deux images d’être capturées par le même capteur au cours de la même orbite. Lorsque le satellite s’approche de sa cible, il peut être pointé vers l’avant pour capturer une image, et plus tard sur l’orbite, il peut être pointé vers l’arrière pour capturer à nouveau la même zone sous un angle différent.

Structure-from-Motion (photogrammétrie multi-image)

Comme il arrive parfois dans le domaine de la télédétection, des techniques développées initialement à d’autres fins (par exemple l’imagerie médicale, l’apprentissage automatique et la vision par ordinateur) présentent un potentiel pour le traitement de l’imagerie de télédétection, et parfois elles finissent par révolutionner une partie de la discipline. C’est le cas de la technique connue sous le nom de Structure-from-Motion (SfM, oui le « f » est censé être minuscule), dont le développement a été influencé par la photogrammétrie, mais a été largement basé dans la communauté de la vision par ordinateur/intelligence artificielle. L’idée de base de la SfM peut être expliquée par un autre parallèlement avec la vision humaine : si la stéréoscopie reproduit la capacité de votre système oculocérébral à utiliser deux vues d’une zone acquises sous des angles différents pour en déduire des informations en 3D, la SfM reproduit votre capacité à fermer un œil et à courir autour d’une zone, en déduisant des informations en 3D à mesure que vous vous déplacez (n’essayez pas cela en classe, mais imaginez comment cela pourrait fonctionner !) En d’autres termes, la SfM est capable de reconstruire un modèle 3D d’une zone à partir de plusieurs images superposées prises avec la même caméra sous différents angles (ou avec des caméras différentes, mais cela devient plus compliqué et est rarement pertinent pour les applications de télédétection).

Il y a plusieurs raisons pour lesquelles la SfM a rapidement révolutionné le domaine de la photogrammétrie, au point que la stéréoscopie traditionnelle pourrait rapidement appartenir au passé. Certaines des différences importantes entre les deux sont énumérées ci-dessous :

• La stéréoscopie traditionnelle (à deux images) exige que la géométrie interne de la caméra soit bien caractérisée. Bien qu’il existe des processus établis pour déterminer cette géométrie, ils exigent un niveau d’expertise moyen et obligent l’utilisateur à calibrer la caméra. La SfM effectue ce calibrage de la caméra en utilisant les mêmes images que celles utilisées pour cartographier la zone d’intérêt.
• Dans le même ordre d’idées, la stéréoscopie traditionnelle exige que la position et l’orientation (le pointage) de la caméra soient connues avec une grande précision pour chaque image. La SfM bénéficie d’informations approximatives sur certains ou tous ces paramètres, mais n’en a pas strictement besoin et est capable de les déduire très précisément des images elles-mêmes. Comme de nombreux appareils photo modernes (comme ceux de votre téléphone) possèdent des récepteurs GPS internes qui fournissent des informations approximatives sur la localisation, les appareils photo grand public peuvent être utilisés pour dériver des modèles numériques d’élévation remarquablement précis.
• Pour les deux techniques, si la position des caméras n’est pas connue, le modèle 3D reconstruit à partir des images peut être géoréférencé à l’aide de points imagés dont la position est connue. De cette façon, les deux techniques sont similaires.
• L’évolution rapide des drones a permis à des personnes ordinaires de disposer d’une plate-forme permettant de déplacer un appareil photo grand public d’une manière qui était auparavant réservée aux personnes ayant accès à des aéronefs pilotés. Les images prises par des caméras grand public basées sur des drones sont exactement le type d’entrée nécessaire dans un flux de travail SfM, alors qu’elles ne fonctionnent pas bien dans le flux de travail traditionnel de stéréoscopie.

Comme nous l’avons mentionné plus haut, SfM utilise plusieurs photos qui se chevauchent pour produire un modèle 3D de la zone imagée sur les photos. Cette opération s’effectue en une série d’étapes, comme indiquée ci-dessous et illustrée à la figure 79 :

Étape 1) identifier les mêmes caractéristiques dans plusieurs images. Pour pouvoir identifier les mêmes caractéristiques dans des photos prises sous différents angles, à différentes distances, avec des appareils photo qui ne sont pas toujours orientés de la même manière, éventuellement dans des conditions d’éclairage différentes, voire dans des cas extrêmes avec des appareils photo différents, SfM commence par identifier les caractéristiques à l’aide de l’algorithme SIFT. Ces caractéristiques sont généralement celles qui se distinguent de leur environnement, comme les coins ou les bords, ou les objets qui sont plus sombres ou plus clairs que leur environnement. Bien que de nombreuses caractéristiques de ce type soient faciles à identifier pour les humains, et que d’autres ne le soient pas, l’algorithme SIFT est spécifiquement conçu pour permettre l’identification des mêmes caractéristiques malgré les difficultés décrites ci-dessus. Cela lui permet de fonctionner particulièrement bien dans le contexte de la SfM.

Étape 2) utiliser ces caractéristiques pour dériver les informations de la caméra intérieure et extérieure ainsi que les positions 3D des caractéristiques. Une fois que plusieurs caractéristiques ont été identifiées dans plusieurs images se chevauchant, un ensemble d’équations est résolu pour minimiser l’erreur de position relative globale des points dans toutes les images. Par exemple, considérons les trois images suivantes (ou plus), dans lesquelles les mêmes points multiples ont été identifiés (représentés par des points de couleur) :

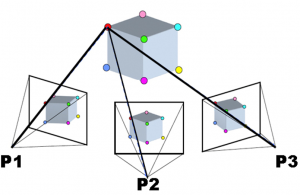
Figure 79: Exemple d’ajustement des blocs de regroupement dans SfM. Sfm1 par Maiteng, Wikimedia Commons, CC BY-SA 4.0.

Sachant que le point rouge de P1 est le même que le point rouge de P2 et P3 et de toutes les autres caméras concernées, et de même pour les autres points, on peut déduire la position relative des deux points et les emplacements et orientations des caméras (ainsi que les paramètres optiques impliqués dans le processus de formation d’image de la caméra). (Notez que le terme « caméra » utilisé ici est identique au terme « image »).

Le résultat initial de ce processus est un emplacement relatif de tous les points et caméras – en d’autres termes, l’algorithme a défini l’emplacement de chaque élément et caméra dans un système de coordonnées tridimensionnel arbitraire. Deux informations supplémentaires peuvent être utilisées pour transformer les coordonnées de ce système arbitraire en coordonnées du monde réel, comme la latitude et la longitude.

Si la géolocalisation de chaque caméra est connue avant ce processus, par exemple si la caméra a produit des images géolocalisées, les emplacements des caméras dans le système de coordonnées arbitraire peuvent être comparés à leurs emplacements réels dans le monde réel, et une transformation des coordonnées peut être définie et également appliquée aux emplacements des éléments identifiés. En outre, si l’emplacement de certaines des caractéristiques identifiées est connu (par exemple, à partir de mesures GPS sur le terrain), une transformation de coordonnées similaire peut être utilisée. Pour les besoins de la télédétection, l’une de ces deux sources d’informations de géolocalisation du monde réel est nécessaire pour que le produit résultant soit utile.

Étape 3) sur la base des caractéristiques maintenant géolocalisées, identifiez d’autres caractéristiques dans plusieurs images et reconstruisez leur position 3D. Imaginez qu’il y ait un petit point gris près du point rouge de la figure 79, disons 1⁄4 du chemin vers le point vert, dans cette direction (il n’y en a pas, c’est pourquoi vous devez l’imaginer !). Ce petit point gris était trop faible pour être utilisé comme une caractéristique SIFT, et n’a donc pas été utilisé pour dériver l’emplacement initial des caractéristiques et les orientations des caméras. Cependant, maintenant que nous savons où trouver le point rouge dans chaque image, et que nous connaissons la position relative de chacun des autres points, nous pouvons estimer où ce point gris devrait se trouver dans chacune des images. Sur la base de cette estimation, nous pourrions effectivement être en mesure de trouver le point gris dans chaque image, et donc d’estimer sa position dans l’espace. Une fois identifiés et localisés dans l’espace, nous pouvons également attribuer une couleur au point, sur la base de sa couleur dans chacune des images où il a été trouvé. Cette opération, qui concerne des millions d’éléments trouvés dans l’ensemble des images, est appelée densification du nuage de points et constitue une étape facultative, mais presque universellement adoptée dans la SfM. Dans les zones où il existe une différence suffisante entre les couleurs des pixels voisins dans les images pertinentes, cette étape peut souvent conduire à la dérivation de l’emplacement de chaque pixel individuel dans une petite zone d’une image. Le résultat de cette étape est donc un « nuage de points » incroyablement dense, dans lequel des millions de points sont localisés dans le monde réel. Un exemple est présenté ci-dessous :

Figure 80: Exemple de nuage de points dense, créé pour une partie du parc de la Gatineau à l’aide d’images de drone. Anders Knudby, CC BY 4.0.

Étape 4) en option, utilisez toutes ces caractéristiques positionnées en 3D pour produire une orthomosaïque, un modèle numérique d’élévation ou tout autre produit utile. Le nuage de points dense peut être utilisé à différentes fins, dont les plus courantes sont la création d’une orthomosaïque et d’un modèle numérique d’élévation. Une orthomosaïque est un type de données matricielles, dans lequel la zone est divisée en cellules (pixels) et la couleur de chaque cellule correspond à ce à quoi elle ressemblerait si elle était vue directement du dessus. Une orthomosaïque est donc semblable à une carte, sauf qu’elle contient des informations sur la couleur de la surface, et représente ce à quoi ressemblerait la zone dans une image prise à une distance infiniment grande (mais avec une très bonne résolution spatiale). Les orthomosaïques sont souvent utilisées seules, car elles donnent aux gens une impression visuelle rapide d’une zone, et elles constituent également la base de la cartographie par la numérisation, la classification et d’autres approches. En outre, comme l’altitude est connue pour chaque point du nuage de points, l’altitude de chaque cellule peut être identifiée afin de créer un modèle numérique de terrain. Différents algorithmes peuvent être utilisés à cette fin, par exemple en identifiant le point le plus bas de chaque cellule pour créer un modèle numérique de terrain « terre nue », ou en identifiant le point le plus haut de chaque cellule pour créer un modèle numérique de surface. Des produits encore plus avancés peuvent être réalisés, par exemple en soustrayant le modèle de terrain nu du modèle de surface pour obtenir des estimations d’éléments tels que la hauteur des arbres et des bâtiments.

Détection des changements à l’aide de la photogrammétrie

Si la création de modèles numériques d’élévation ou d’autres produits à l’aide de la stéréoscopie ou de la méthode de la structure à partir du mouvement peut être utile en soi, une application de plus en plus courante de ces techniques est la détection des changements de surface. Si, par exemple, un modèle numérique d’élévation est créé pour un glacier une année, et un nouveau deux ans plus tard, les changements de forme de la surface du glacier peuvent être cartographiés avec une grande précision. Les glissements de terrain, les effondrements dus au dégel, les changements de végétation, les variations de l’épaisseur de la neige au cours d’une saison — de nombreux changements dans l’environnement physique peuvent être détectés et quantifiés en mesurant les changements de la position horizontale ou verticale de la surface de la Terre. Étant donné le développement relativement récent de la technologie SfM, et les capacités encore en développement et le coût des drones équipés de caméras, il s’agit d’un domaine en développement rapide susceptible d’être utile dans des parties surprenantes et insoupçonnées du domaine de la télédétection. La figure 81 illustre ce principe en comparant le profil du glacier et les changements d’élévation de la surface à deux moments différents.

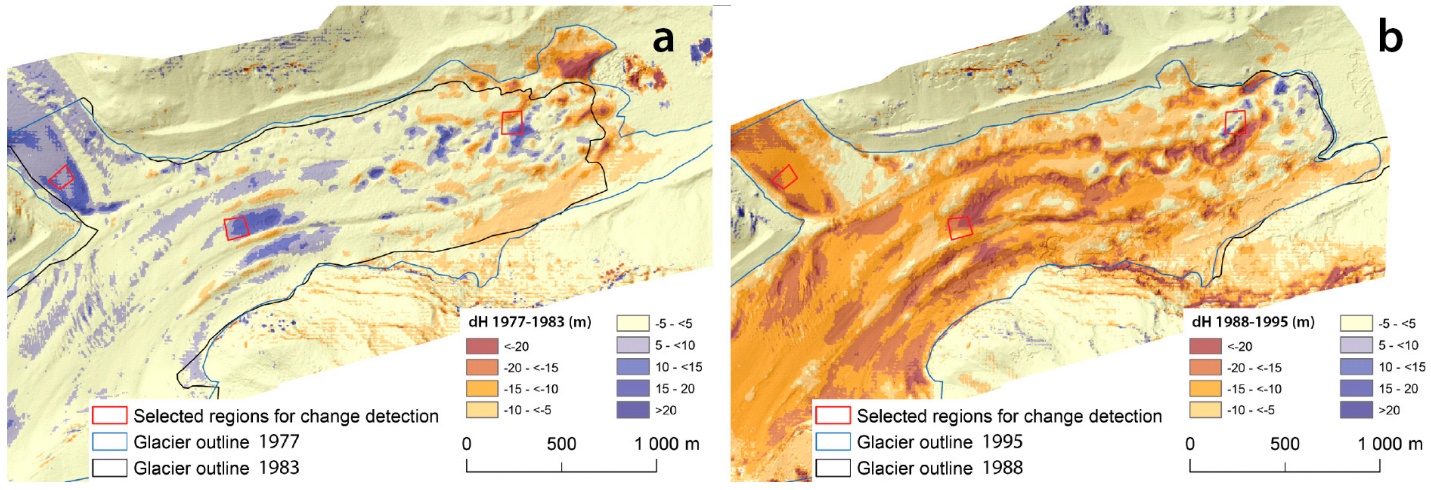
Figure 81: Détection de changement 3D basée sur la SfM répétée. Structure-from-Motion Using Historical Aerial Images to Analyse Changes in Glacier Surface Elevation (Figure 7) par Mölg and Bolch, CC BY 4.0.