Solutions
Chapter 1 – Numbers
1.1
1.1
2.1
Answers may vary. Some of the patterns are:
The left column can be divided in 4 groups, with each group possessing 19, 17, 13, and 11 notches. The sum of these being 60. Those are the 4 successive prime numbers between 10 and 20.
The central column is divided in groups of 8. By an approximate count, one can find (in the parenthesis, is the maximum number): 7 (8), 5 (7), 5 (9), 10, 8 (14), 4 (6), 6, 3. The minimal sum is 48, while the maximal sum is 63.
The right column is divided into 4 groups, where each group has 9, 19, 21, and 11 notches. The sum of these 4 numbers is 60.
The numbers in the left column were compatible with a numeration system based on 10, since 21 = 20 + 1, 19 = 20 – 1, 11 = 10 +1, and 9 = 10 -1. These numbers are also prime numbers between 10 and 20: 11, 13, 17, 19.
1.2
1.1
2.1
1) How many symbols did the Babylonians use to express numbers?
2 unique symbols in 60 different arrangements.
2) In our decimal system we have 10 digits 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. How many digits did the Babylonians have?
60 digits
3) Calculate the value of
a) 2 x 60 = 120, 6 x 1 = 6
126
b) 2 x 60 = 120, 12 x 1 = 12
132
c) 10 x 3600 = 36000, 10 x 60 = 600, 2 x 1 = 2
36602
d) How would Babylonians write 65? 615? 665?

1.3
1.1
2.1
A granary of barley contains 2400 gur, where 1 gur equals 480 sila. If workers are to receive 7 sila of grain for a day’s work, how many men can be paid from this granary?
[latex]\begin{array}{l}1\ gur\ =\ 480\ sila\\ 2400\ gur\ =\ 2400\ x\ 480\ sila\ =\ 115200\ sila\\ divide\ by\ 7\ sila\ per\ wor\ker\\ \frac{115200\ sila}{7\ \frac{sila}{wrkr}}\approx16457.142\ wrkrs\end{array}[/latex]
1.4
1.1
2.1
A woman weaves a textile that is to be 48 rods long. In one day, she weaves 1/3 rod. In how many days will she cut the textile from the loom?
Length = 48 rods
Rate = ⅓ rod / day
Total time = ? days
[latex]\begin{array}{l}total\ time\ =\ \frac{total\ length}{rate}\\ =\frac{48\ rods}{\frac{1}{3}rod\ per\ day}=\frac{48\cdot3}{1}=48\cdot3=144\ rods\end{array}[/latex]
1.5
1.1
2.1
a) Find values of the numbers
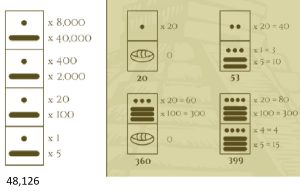
b) Write numbers 85, 121 and 2222 in Mayan numerals
1.6
1.1
2.1
There is a tree with 100 branches; each branch has 100 nests; each nest, 100 eggs; each egg, 100 birds. How many nests, eggs and birds are there?
100 branches per tree (100)
100 nests per branch (100 x 100=10000 nests)
100 eggs per nest (100 x 10000 = 1000000 eggs)
100 birds per egg (100 x 1000000 = 100000000 birds)
Total nests, eggs, and birds = 10000 + 1000000 + 100000000 = 101010000 total objects
1.7
1.1
2.1
Three hundred pigs are to be prepared for a feast. They are to be prepared in three batches on three successive days with an odd number of pigs in each batch. Can this be accomplished?
Odd + Odd = even
Odd + Even = odd
Three batches: Odd + Odd + Odd
Since Odd + Odd = even, then: Odd + Odd + Odd = Even + Odd = Odd.
Since there are 300 pigs (which is even), no this is not possible.
1.8
1.1
2.1
A leech invited a slug for lunch a leuca away. But he could only crawl an inch a day. How long will it take the slug to get his meal? [1 leuca = 1500 paces; 1 pace = 5 feet.]
1 leuca = 1500 paces
1500 paces = 1500 x 5 feet = 7500 feet
7500 feet = 7500 x 12 inches = 90000 feet
Therefore, it will take 90000 days for the slug to get his meal.
90000 days at 365 days per year = 246 years with a remainder of 210 days.
1.9
1.1
2.1
A certain man had in his trade four weights with which he could weigh integral pounds from 1 up to 40. How many pounds was each weight?
1, 3, 9 and 27.
| Weight of object to be measured | Left side | Right side |
| 1 | O | 1 |
| 2 | O, 1 | 3 |
| 3 | O | 3 |
| 4 | O | 3, 1 |
| 5 | O, 3, 1 | 9 |
| 6 | O, 3 | 9 |
| 7 | O, 3 | 9, 1 |
| 8 | O, 1 | 9 |
| 9 | O | 9 |
| 10 | O | 9, 1 |
| 11 | O, 1 | 9, 3 |
| 12 | O | 9, 3 |
| 13 | O | 9, 3, 1 |
| 14 | O, 9, 3, 1 | 27 |
| 15 | O, 9, 3 | 27 |
| 16 | O, 9, 3 | 27, 1 |
| 17 | O, 9, 1 | 27 |
| 18 | O, 9 | 27 |
| 19 | O, 9 | 27, 1 |
| 20 | O, 9, 1 | 27, 3 |
| 21 | O, 9 | 27, 3 |
| 22 | O, 9 | 27, 3, 1 |
| 23 | O, 3, 1 | 27 |
| 24 | O, 3 | 27 |
| 25 | O, 3 | 27, 1 |
| 26 | O, 1 | 27 |
| 27 | O | 27 |
| 28 | O | 27, 1 |
| 29 | O, 1 | 27, 3 |
| 30 | O | 27, 3 |
| 31 | O | 27, 3, 1 |
| 32 | O, 3, 1 | 27, 9 |
| 33 | O, 3 | 27, 9 |
| 34 | O, 3 | 27, 9, 1 |
| 35 | O, 1 | 27, 9 |
| 36 | O | 27, 9 |
| 37 | O | 27, 9, 1 |
| 38 | O, 1 | 27, 9, 3 |
| 39 | O | 27, 9, 3 |
| 40 | O | 27, 9, 3, 1 |
1.10
1.1
2.1
I have a cloak 100 cubits long and 80 cubits wide. I wish to make small cloaks with it; each small cloak is 5 cubits long, and 4 wide. How many small cloaks can I make?
Since 5 divides into 100 and 4 divides into 80, we can assume that all of the fabric will be used if we orient the small cloaks such that their 5 cubit sides align along the 100 cubit side of the large cloak, and the 4 cubit sides along the 80 cubit.
Along the long side, we can fit 20 (100/5) small cloaks in a row.
Along the short side, we can fit 20 (80/4) small cloaks in a row.
Therefore we have an array of 20 small cloaks by 20 small cloaks. The total is 400 cloaks.
1.11
1.1
2.1
A father, when dying, gave to his sons 30 glass flasks, of which 10 were full of oil, 10 were half full, and the last 10 were empty. Divide the oil and the flasks so that each of the three sons received equally of both glass and oil.
Each son needs to receive 10 actual flasks (glass)
There is a total of 10 x 1 + 10 x 0.5 = 15 flasks worth of oil. Therefore each son needs to receive 5 flasks worth of oil.
One possible solution is to give:
Son 1 – 5 full and 5 empty
Son 2 – 5 full and 5 empty
Son 3 – 10 half-empty
1.12
1.1
2.1
A king ordered his servants to collect an army from 30 manors in such a way that from each manor he would take the same number of men he had collected up until then. The servant went to the first manor alone; to the second he went with one other; to the next he took three with him. How many were collected from the 30 manors?
| Manor # | How many brought | Collected at this | New Total |
| 1 | 0 | 1 | 1 |
| 2 | 1 | 1+1=2 | 3 |
| 3 | 3 | 2+3=5 | 8 |
| 4 | 8 | 5+8=13 | 21 |
| 5 | 21 | 13+21=34 | 55 |
| 6 | 55 | 34+55=89 | 144 |
| 7 | 144 | 89+144=233 | 377 |
| 8 | 377 | 233+377=610 | 987 |
| 9 | 987 | 610+987=1597 | 2584 |
| 10 | 2584 | 1597+2584=4181 | 6765 |
| 11 | 6765 | 4181+6765=10946 | 17711 |
| 12 | 17711 | 10946+17711=28657 | 46368 |
| 13 | 46368 | 28657+46368=75025 | 121393 |
| 14 | 121393 | 75025+121393=196418 | 317811 |
| 15 | 317811 | 196418+317811=514229 | 832040 |
| 16 | 832,040 | 514229+832040=1,346,269 | 2,178,309 |
| 17 | 2,178,309 | 1,346,269+2,178,309=
3,524,578 |
5,702,887 |
| 18 | 5,702,887 | 3,524,578+ |
1.13
1.1
2.1
A gentleman has a household of 30 people and orders that they be given 30 measures of grain. He directs that each man should receive 3 measures, each woman 2 measures, and each child 1/2 measure. How many men, women, and children are there?
The solution can be found by trial and error method.
3 men, 5 women, 22 children
1.14
1.1
2.1
A man wanting to build a house contracted with six builders, five of whom were master builders, and the sixth an apprentice, to build it for him. He agreed to pay them a total of 25 pence a day, with the apprentice to get half the rate of a master builder. How much did each receive per day?
A master builder got 4.54 and apprentice got 2.27 pence a day.
1.15
1.1
2.1
A man in the east wanted to buy 100 assorted animals for 100 shillings. He ordered his servant to pay 5 shillings for a camel, 1 shilling for an ass, and 1 shilling for 20 sheep. How many camels, asses, and sheep did he buy?
The solution can be found by trial and error method or by making a list.
19 camels, 1 ass and 80 sheep
1.16
1.1
2.1
There is an estate that contains 7 houses; each house has 7 cats; each cat catches 7 mice; each mouse eats 7 spelt of seeds; each spelt was capable of producing 7 hekats of grain. How many things were in the estate?
7 + 49 + 343 + 2401 + 16,807.= 19,607
1.17
1.1
2.1
Suppose a scribe tells you that four overseers have drawn 100 great quadruple hekats of grain, and their work gangs consist of 12, 8, 6, and 4 men. How much grain does each overseer receive?
100 / (12 + 8 + 6 + 4)= 3 1/3
12(3 1/3)= 40
8(3 1/3) = 26 2/3
6(3 1/3)= 20
4(3 1/3)= 13 1/3
1.18
1.1
2.1
In the middle register we see 835 horned cattle on the left, right behind them are some 220 animals (cows?) and on the right 2235 goats. In the bottom register we see 760 donkeys on the left and 974 goats on the right
1.19
1.1
2.1
1.20
1.1
2.1
Given, four whole numbers where, if added together three at a time, their sums are 20, 22, 24, and 27. What are the numbers?
Suppose the numbers are a, b, c and d. Then:
a+b+c = 20
b+c+d = 22
a+c+d = 24
a+b+d = 27
If we add all of these equations together we find:
3(a+b+c+d) = 22+24+27+20 = 93
Dividing both ends by 3 we find:
a+b+c+d = 93/3 = 31
Then we can find the values of a, b, c and d:
a = (a+b+c+d) – (b+c+d) = 31-22 = 9
b = (a+b+c+d)-(a+c+d) = 31-24=7
c = (a+b+c+d)-(a+b+d) = 31-27 = 4
d = (a+b+c+d)-(a+b+c) = 31-20 = 11
Chapter 2 – Circles
2.1
1.1
2.1
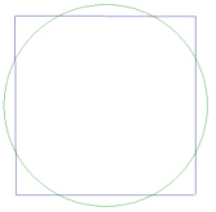
One of the geometric rules given in the Talmud is “How much is the square greater than the inscribed circle? A quarter” What was the Talmudic value for pi?
Case 1 – Assuming we are discussing area, then:
Let S be the area of the square
Let C be the area of the circle
l (of square) = d = 2r
S = 1.25C
Therefore:
[latex]\begin{array}{l}l^2=\pi r^2\\ substituting\ 2r\ for\ l:\left(2r\right)^2=\pi r^2\\ 4r^2=\pi r^2\\ 4=\pi\end{array}[/latex]
Case 2 – if we are discussing circumference:
[latex]\begin{array}{l}S=1.25C\\ l=d\\ 4d=1.25\pi d\\ 1.25\pi=4\\ \pi=\frac{4}{1.25}=\frac{16}{5}=3.2\end{array}[/latex]
Although the wording of the question seems to suggest area as the measurement being discussed in this question, the calculation for pi in the circumference solution is much closer to the modern value of pi than the area solution.
2.2
1.1
2.1
In 4000 year old Egyptian papyrus we read “A circular field has diameter 9 chet. What is its area?” The Ahmes, the scribe of the papyrus, gives the solution: “Subtract 1/9 of the diameter namely 1 chet. The remainder is 8 chet. Multiply 8 by 8; it makes 64. Therefore, it contains 64 square chet of land”
For the Egyptians a square with the side length 8/9 of the diameter of a circle was a good enough approximation to calculate the area of a circle.
Calculate the ancient Egyptian value of pi.
[latex]A=\ \left(\frac{8}{9}d\right)^2[/latex]
If we substitute the modern formula for area of a circle, we can solve for pi:
[latex]\begin{array}{l}A=\ \left(\frac{8}{9}d\right)^2\\ \pi r^2=\left(\frac{8}{9}d\right)^2\\ d=2r\\ \pi r^2=\left(\frac{16r}{9}\right)^2\\ \pi r^2=\frac{256r^2}{81}\\ \pi=\frac{256r^2}{81r^2}=\frac{256}{81}\end{array}[/latex]
Therefore π = 256/81≈ 3.16
2.3
1.1
2.1
In Babylonian mathematics a circle was equated to a regular hexagon which side was equal to the radius of a circle. Calculate the Babylonian value of pi.

The perimeter of the hexagon is P≅6r. The circumference C=2πr. 2π=6 π=3
2.4
1.1
2.1
There is a round field which contains 400 yards in its circumference. How many square yards will its area be? Alcuin obtains 10000 square yards. How does he get that, you might ask? Calculate the value of pi he used.
We begin with the formulas for Area of a Circle and Circumference of a Circle:
[latex]\begin{array}{l}A=\pi r^2\\ C=2\pi r\end{array}[/latex]
(Note the use of the radius-centred circumference formula, rather than the diameter formula. This is done to preserve variables)
We know that C = 400, and A = 10000. Therefore, we can solve for pi.
[latex]\begin{array}{l}10000=\pi r^2\\ 400=2\pi r\\ r=\frac{400}{2\pi}\\ \therefore10000=\pi\left(\frac{400}{2\pi}\right)^2\\ 10000=\frac{160000\pi}{4\pi^2}\\ 10000=\frac{40000}{\pi}\\ 10000\pi=40000\\ \pi=4\end{array}[/latex]
2.5
1.1
2.1
There is a city which is 8000 feet in circumference. How many houses could the city contain if each house is 30 feet long and 20 feet wide?
There are two scenarios here. The first, which is the simplistic scenario, is the assumption that the shape of the houses can be squished into a shape to meet the curve of the circle of the city. Assuming unrealistic city design where each house was connected to each other like bricks and there were no additional buildings or spaces within the city, we can calculate the theoretical maximum number of houses. Each house has a constant area of 600 square feet, notwithstanding some slight variance in the shape of each house to accommodate the curved edges of the city. Therefore the theoretical maximum (TM) is the area of the circle in square feet divided by 600 square feet per house.
[latex]\begin{array}{l}TM=\frac{A}{600}\\ A=\pi r^2\\ C=2\pi r\\ If\ C=8000\\ then\ 8000=2\pi r\\ r=\frac{8000}{2\pi}=\frac{4000}{\pi}\\ TM=\frac{\pi r^2}{600}\\ =\frac{\pi\left(\frac{4000}{\pi}\right)^2}{600}\\ =\frac{16000000}{600\pi}\\ =\frac{80000}{3\pi}\\ If\ we\ take\ \pi\ \approx3.1415\\ TM\approx8488.26\end{array}[/latex]
Therefore the theoretical maximum if every square foot of the city was house (unrealistic) is 8488 houses. Answers will vary, and the solutions need to be justified based on realistic considerations, such as:
- Other buildings (businesses, markets, schools, community centres, religious buildings, government buildings, utility buildings, etc.)
- Open spaces (paths, roads, squares, etc.)
- Green space (parks, plazas, hiking trails, etc.)
- Attractions (fairs, sports centres, arts centres, etc.)
- Topography (whether there are hills, valleys, rivers, etc.)
- Transportation requirements (stables, bus facilities, trains, airport, etc.)
- How much space people take up in a city when outside their homes
- And perhaps most importantly, the fact that buildings need to have separation from each other, and not be squished together in all directions.
2.6
1.1
2.1
A circular road A that is 48 km in circumference touches at point P another circular road B of circumference 36 km. A cow and a horse start walking from the point P along the road A and B, respectively. The cow walks 6 km per day and the horse walks 12 km per day. How many days later days later do the cow and horse meet again at P?
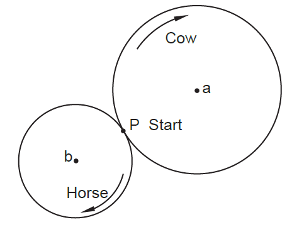
The cow walks the full circle A in 48/6 = 8 days. The horse walks the full circle B in 36/12 = 3 days. Finding the lowest common multiple, which is 3×8=24, we find that 24 days later the cow and horse meet again at P
2.7
1.1
2.1
A circle of radius r is inscribed in an isosceles triangle with sides 10 and 12. Find r.
Draw the diagram with some auxiliary lines

Label the vertices. By the Pythagorean theorem BN=8.
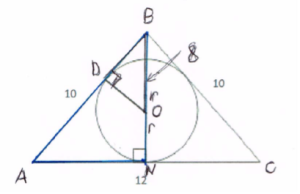
We can see now that triangles ABN and ODB are similar (the angles are equal). For better visual we overlap them. Label the sides in the diagram by their length.

Now we can write the ratio AN : AB = OD : DB or 6 : 10 = r : (8-2r).
r=3.
2.8
1.1
2.1
The centers of a loop of the circles of radius r form the vertices of a polygon, as shown in the figure below. Let S1 be the sum of the shaded areas of the circles, and S2 the sum of the unshaded areas of the circles. Find [latex]S2 S1.[/latex]
Match the shaded and unshaded pieces. Then count the rest of unshaded pieces. If you combine them you get two full circles. Therefore [latex]S2 S1 = 2πr2[/latex]

Chapter 3 – Area and Volume
3.1
1.1
2.1
Find the volume of a cylindrical granary of diameter 9 cubits and height 10 cubits. (1 cubit = 52 cm)
If we want to find the volume in cubits:
Let [latex]\begin{array}{l}V=\end{array}[/latex] the volume of the cylindrical granary in cubits
[latex]\begin{array}{l}V=\text{area of base}\cdot\text{height}\\ V=(\pi\cdot r^2)\cdot h\\ V=\pi\cdot (\frac{9}{2})^2\cdot 10\\ V=\pi\cdot 4.5^2\cdot 10\\ V=\pi\cdot 20.25\cdot 10\\ V=\pi\cdot 202.5\\ V\approx 636.17\\ \end{array}[/latex]
Therefore the volume of this cylindrical granary is approximately 636.17 cubic cubits.
If we want to find the volume in centimeters:
1 cubit:52 cm
If there were a cube of 1 cubit, its volume would be calculated as [latex]\begin{array}{l}l\cdot w\cot h=1\cdot 1\cdot 1=1^3=1\end{array}[/latex]
Therefore its volume would be 1 cubic cubit.
The same cube could be said to be of 52 cm, and the same volume would be calculated as [latex]\begin{array}{l}52\cdot 52\cdot 52=140608\end{array}[/latex]
Therefore the volume of 140,608 cm[latex]\begin{array}{l}^3\end{array}[/latex] is equal to 1 cubic cubit.
1 cubic cubit:140,608 cm[latex]\begin{array}{l}^3\end{array}[/latex]
Let [latex]\begin{array}{l}V=\end{array}[/latex] the volume of the cylindrical granary in cubic centimeters.
[latex]\begin{array}{l}1\text{ cubic cubit}:140,608\text{ cm}^3\\ 202.5\pi\text{ cubic cubits}:V\text{ cm}^3\\ \\ V=140608*202.5\pi\\ =89450944.62\\ \end{array}[/latex]
Therefore the volume of this cylindrical granary is approximately 89,450,944.62 cm[latex]\begin{array}{l}^3\end{array}[/latex]
3.2
1.1
2.1
Find the volume of a cylindrical granary of diameter 10 cubits and height 10 cubits. (1 cubit = 52 cm)
If we want the volume in cubic centimeters, we can start by converting the measure of diameter and height from cubits to cm:
Let [latex]\begin{array}{l}d=\end{array}[/latex] the diameter in cm.
[latex]\begin{array}{l}1\text{ cubit}:52\text{ cm}\\ 10\text{ cubits}:d\text{ cm}\\ \\ d=52*10\\ =520\\ \end{array}[/latex]
Therefore the diameter is 520 cm.
Let [latex]\begin{array}{l}h=\end{array}[/latex] the height in cm.
[latex]\begin{array}{l}1\text{ cubit}:52\text{ cm}\\ 10\text{ cubits}:h\text{ cm}\\ h=52*10\\ =520\\ \end{array}[/latex]
Therefore the height is 520 cm.
The volume of a cylindrical container is the product of the container’s height and the area of its circular base.
Let [latex]\begin{array}{l}V=\end{array}[/latex] the volume of the cylindrical granary in cubic centimeters.
[latex]\begin{array}{l}V=\text{Area of base}\cdot\text{height}\\ V=(\pi\cdot r^2)\cdot h\\ V=\pi\cdot (\frac{520}{2})^2\cdot 520\\ V=\pi\cdot 260^2\cdot 520\\ V=\pi\cdot 67600\cdot 520\\ V=\pi\cdot 35152000\\ V\approx 110433264.96\\ \end{array}[/latex]
Therefore the volume of this cylindrical granary is approximately 110,433,264.96 cm[latex]\begin{array}{l}^3\end{array}[/latex]
If we want to convert this into cubic cubits:
Let [latex]\begin{array}{l}V=\end{array}[/latex] the volume of the cylindrical granary in cubic cubits.
From 3.1, we know that:
[latex]\begin{array}{l}1\text{ cubic cubit}:140,608 cm^3\\ V\text{ cubic cubits}:35,152,000\pi\text{ cubic centimeters}\\ \\ V=\frac{35152000\pi}{140608}\\ V\approx 785.40\\ \end{array}[/latex]
Therefore, the volume of this cylindrical granary is approximately 785.40 cubic cubits.
3.3
1.1
2.1
A cylindrical granary of diameter 9 cubits and height 6 cubits. What is the amount of grain that goes into it? (1 cubit = 52 cm. The hekat was an ancient Egyptian volume unit used to measure grain, bread, and beer. It equals 4.8 litres. 30 hekats equals 1 cubic cubit)
By asking for the amount of grain that fits within a cylindrical granary, this question is asking for this granary’s volume; the volume of a cylindrical container is the product of the container’s height and the area of its circular base.
[latex]\begin{array}{l}V=\text{area of base}\cdot\text{height}\\ V=(\pi\cdot r^2)\cdot h\\ V=\pi\cdot (\frac{9}{2})^2\cdot 6\\ V=\pi\cdot 4.5^2\cdot 6\\ V=\pi\cdot 20.25\cdot 6\\ V=\pi\cdot 121.5\\ V\approx 381.70\\ \end{array}[/latex]
Therefore the volume of this cylindrical granary is approximately 381.70 cubic cubits.
As 30 hekats equals 1 cubic cubit, we can multiply this volume by 30 to get the amount of grain being stored.
Let [latex]\begin{array}{l}q=\end{array}[/latex] the quantity of grain being stored in the 381.70 cubic cubits cylindrical granary.
[latex]\begin{array}{l}q=381.70\cdot 30\\ q=11451.10\\ \end{array}[/latex]
Therefore there is approximately 11,451.10 hekat of grain being stored in this cylindrical granary.
3.4
1.1
2.1
A rectangular granary into which there have gone 7500 quadruple hekat of grain. What are its dimensions? (The hekat was an ancient Egyptian volume unit used to measure grain, bread, and beer. It equals 4.8 litres.)
First we convert the quantity of grain into the measure of volume of the container.
From Question 3.3, we know that 1 cubic cubit of volume is equal to 30 hekat of grain.
We want to know the volume in cubic cubits that corresponds with 7500 quadruple hekat of grain.
Let [latex]\begin{array}{l}x=\end{array}[/latex] the amount of 7500 quadruple hekat in units of hekat.
[latex]\begin{array}{l}7500:x\\ 1:4\\ \frac{7500}{x}=\frac{1}{4}\\ 7500=x\cdot\frac{1}{4}\\ 7500\cdot 4=x\\ 30000=x\\ \end{array}[/latex]
Therefore 7500 quadruple hekat – where 1 quadruple hekat is equivalent to 4 hekat – is equal to 30,000 hekat.
Let [latex]\begin{array}{l}v=\end{array}[/latex] the volume of the rectangular granary in cubic cubits.
[latex]\begin{array}{l}1:30\\ v:30000\\ \frac{1}{30}=\frac{v}{30000}\\ 30000\cdot\frac{1}{30}=v\\ 1000=v\\ \end{array}[/latex]
Therefore the volume of the rectangular granary is 1000 cubic cubits.
The volume of a rectangular container is the product of the container’s height and the area of its base.
[latex]\begin{array}{l}V=\text{area of base}\cdot\text{height}\\ V=(l\cdot w)\cdot h\\ 1000=l\cdot w\cdot h\\ \end{array}[/latex]
There are multiple possible dimensions for this rectangular granary, as there are multiple dimensions that meet the requirement of being 10,000 cubic cubits in volume.
We can solve for a set of possible dimensions if we make additional assumptions. E.g., the rectangular granary is actually a perfect cube where its length, width, and height are all equal.
[latex]\begin{array}{l}l=w=h\\ \text{therefore: }\\ 1000=l\cdot w\cdot h\\ 1000=w\cdot w\cdot w\\ 1000=w^3\\ \sqrt[3]{1000}=\sqrt[3]{w^3}\\ 10=w\\ \end{array}[/latex]
Therefore, based on the additional assumption, we have the dimensions of a cube granary with side length of 10 cubits.
3.5
1.1
2.1
A rectangular granary into which there have gone 2500 quadruple hekat of grain. What are its dimensions? (The hekat was an ancient Egyptian volume unit used to measure grain, bread, and beer. It equals 4.8 litres.)
First we convert the quantity of grain into the measure of volume of the container.
From Question 3.3, we know that 1 cubic cubit of volume is equal to 30 hekat of grain.
We want to know the volume in cubic cubits that corresponds with 2500 quadruple hekat of grain.
Let [latex]\begin{array}{l}y=\end{array}[/latex] the amount of 2500 quadruple hekat in units of hekat.
[latex]\begin{array}{l}2500:y\\ 1:4\\ \frac{2500}{y}=\frac{1}{4}\\ 2500 = y\cdot\frac{1}{4}\\ 2500\cdot 4=y\\ 10000=y\\ \end{array}[/latex]
2500 quadruple hekat – where 1 quadruple hekat is equivalent to 4 hekat – is equal to 10,000 hekat.
Let [latex]\begin{array}{l}v=\end{array}[/latex] the volume of the rectangular granary in cubic cubits.
[latex]\begin{array}{l}1:30 = v:10,000\\ \frac{1}{30}={v}{10000}\\ 10000\cdot\frac{1}{30}=v\\ 333\frac{1}{3}=v\\ \end{array}[/latex]
Therefore the volume of the rectangular granary is [latex]\begin{array}{l}333\frac{1}{3}\end{array}[/latex] cubic cubits.
The volume of a rectangular container is the product of the container’s height and the area of its base.
[latex]\begin{array}{l}V=\text{area of base}\cdot\text{height}\\ V=(l*w)*h\\ 333\frac{1}{3}=l*w*h\\ \end{array}[/latex]
We can solve for a set of possible dimensions if we make additional assumptions. E.g., the rectangular granary is actually a perfect cube where its length, width, and height are all equal.
[latex]\begin{array}{l}l=w=h\\ \\ 333\frac{1}{3}=l\cdot w\cdot h\\ 333\frac{1}{3}=w\cdot w\cdot w\\ 333\frac{1}{3}=w^3\\ \sqrt[3]{333\frac{1}{3}}=\sqrt[3]{w^3}\\ w \approx 6.93\\ \end{array}[/latex]
Therefore, based on our additional assumption, we have the dimensions of a cube granary with side length of approximately 6.93 cubits.
3.6
1.1
2.1
Suppose it is said to thee. What is the area of a triangle of side 10 khet and of base 4 khet? (1 khet = 100 cubits, 1 cubit = 52 cm. Assume the triangle is isosceles).
Let [latex]\begin{array}{l}b=\end{array}[/latex] the measure of the base of the triangle in khet,
let [latex]\begin{array}{l}s=\end{array}[/latex] the measure of the side length of the triangle in khet, and
let [latex]\begin{array}{l}A=\end{array}[/latex] the area of the triangle in square khet.
The area of an isosceles triangle of side 10 khet and base 4 khet is half of the area of a rectangle of side 10 khet and base 4 khet. The area of the rectangle is the product of the base and the side length: [latex]\begin{array}{l}b\cdot s\end{array}[/latex]. Therefore the area of the triangle is [latex]\begin{array}{l}\frac{b\cdot s}{2}\\ \\ A=\frac{b\cdot s}{2}\\ A=\frac{4\cdot 10}{2}\\ A=\frac{40}{2}\\ A=20\\ \end{array}[/latex]
Therefore the area of the triangle is 20 square khet.
3.7
1.1
2.1
Suppose it is said to thee, What is the area of a cut-off (truncated) triangle of land of 20 khet in its side, 6 khet in its base, 4 khet in its cut-off line? (1 khet = 100 cubits, 1 cubit = 52 cm. Assume the triangle is isosceles).
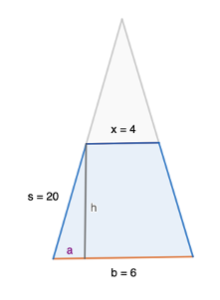
[latex]\begin{array}{l}\text{Area of a Trapezoid}=\frac{x+b}{2}\cdot h\end{array}[/latex]
To determine h, we can use Pythagorean Theorem on the right-angle triangle made by a vertical line connecting the two horizontal lines, x and b.
[latex]\begin{array}{l}a^2+b^2=c^2\\ a^2+h^2=s^2\\ a^2+h^2=20^2\\ \end{array}[/latex]
a is the measure between the far left point to where the height line meets the base, b. The same length also occurs on the right side of the triangle. Therefore, this measurement is half of the difference between the two lines: [latex]\begin{array}{l}a=\frac{b-x}{2}\\ \\ \frac{b-x}{2}\\ =\frac{6-4}{2}\\ =\frac{2}{2}\\ =1\\ \\ a^2+h^2=20^2\\ 1^2+h^2=20^2\\ 1+h^2=400\\ h^2=400-1\\ h=\sqrt(399)\\ \\ \text{area of trapezoid}}=\frac{x+b}{2}\cdot h\\ =\frac{4+6}{2}\cdot\sqrt(399)\\ =\frac{10}{2}\cdot\sqrt(399)\\ =5\cdot\sqrt(399)\\ \end{array}[/latex]
Therefore the area of the land is [latex]\begin{array}{l}5\cdot\sqrt(399)\end{array}[/latex] square khet.
3.8
1.1
2.1

The body of the human and its parts were considered as the most effective scales for measuring in all cultures. The limbs were considered as the best scales for measurement because they allowed instant measurements. You don’t need a ruler! Your ruler is always with you. The following are some old Mongolian units of length. Can you match them with the body parts pictured in the diagram above?
● Huruu 1.5–2 cm
● Yamh 3.5 cm
● üzür sööm 18 cm
● ald 1.6 m
● sööm – 16 cm
[latex]\begin{array}{|c|c|c|c|} \hline\ \text{Unit} & \text{In Metric} & \text{Pic Number} & \text{Reasoning}\\ \hline \text{Huruu} & 1.5–2\text{cm} & 4\text{. Finger nail} & \text{smallest}\\ \hline \text{Yamh} & 3.5\text{cm} & 5\text{. Finger tip} & \text{second smallest}\\ \hline \text{üzür sööm} & 18\text{cm} & 3\text{. Hand span} & \text{second largest}\\ \hline \text{ald} & 1.6\text{m} & 1\text{. Wing span} & \text{largest}\\ \hline \text{sööm} & 16\text{cm} & 2\text{. Pointer to thumb} & \text{process of elimination}\\ \hline \end{array}[/latex]
3.9
1.1
2.1
The most ancient inscription found so far in Mongolian language is carved onto the stone known as Genghis Khan’s stone. It is dated around 1225 and immortalizes one of Genghis Khan’s warrior’s archery achievement:
“When Chinggis Khan was holding an assembly of Mongolian nobles at Bukha-(S)ochiqai after he had come back from the conquest of the Sartuul people, Yisüngke hit a target at 335 alds.”
● How far is the target in meters?
● Do you think that this feat is achievable?
Let [latex]\begin{array}{l}d=\end{array}[/latex] the distance of the target in meters.
[latex]\begin{array}{l}335\text{ ald}:d\text{ meters}\\ \text{From 3.8, we know that 1 ald is equal to 1.6 meters.}\\ 1\text{ ald}:1.6\text{ m}\\ \frac{335}{1}=\frac{d}{1.6}\\ 1.6\cdot 335=d\\ 536=d\\ \end{array}[/latex]
Therefore, 335 ald is equivalent to 536 meters.
Do I think this feat is achievable? Hitting a target more than half a kilometer away? No. I think that the target would be difficult to discern at that distance, let alone be able to hit it accurately! And that is not to mention the quality needs of the bow to travel that distance – with precision, no less!
3.10
1.1
2.1
A basilica is 240 feet long and 120 feet wide. The basilica paved with tiles 23 inches long and 12 inches wide. How many tiles are needed to cover the basilica? (There are 12 inches in a foot.)
Let [latex]\begin{array}{l}t=\end{array}[/latex] the length of the basilica tiles in feet.
[latex]\begin{array}{l}12\text{ inches}:1\text{ foot}\\ 23\text{ inches}:t\text{ feet}\\ \frac{12}{23}=\frac{1}{t}\\ t=\frac{1\cdot 23}{12}\\ t=\frac{23}{12}\\ t=1\frac{11}{12}\\ 23\text{ inches}=1\frac{11}{12}\text{ feet}\\ \end{array}[/latex]
In feet:
Let [latex]\begin{array}B=\end{array}[/latex] the area of the basilica in sqft.
Let [latex]\begin{array}T=\end{array}[/latex] the area of each tile in sqft.
Let [latex]\begin{array}N=\end{array}[/latex] the number of tiles needed to fill the basilica.
[latex]\begin{array}{l}B=\text{length}\cdot\text{width}\\ =240\cdot 120\\ =28800\\ \end{array}[/latex]
Therefore, the area of the basilica is 28,800 sqft.
[latex]\begin{array}{l}T=\text{length}\cdot\text{width}\\ =1\frac{11}{12}\cdot 1\\ =1\frac{11}{12}\\ \end{array}[/latex]
Therefore, the area of each tile is [latex]\begin{array}1\frac{11}{12}\end{array}[/latex] sqft.
[latex]\begin{array}{l}N=\frac{B}{T}\\ =\frac{28800}{1\frac{11}{12}}\\ \approx 15026.09\\ \end{array}[/latex]
Therefore, we need 15,027 tiles.
In inches:
Let [latex]\begin{array}B=\end{array}[/latex] the area of the basilica in square inches.
Let [latex]\begin{array}T=\end{array}[/latex] the area of each tile in square inches.
Let [latex]\begin{array}N=\end{array}[/latex] the number of tiles needed to fill the basilica.
[latex]\begin{array}{l}240\text{ ft}\cdot 12\frac{\text{in}}{\text{ft}}=2880\text{in}\\ 120\text{ ft}\cdot 12\frac{\text{in}}{\text{ft}}=1440\text{ in}\\ \text{Therefore, the dimensions of the basilica are 2880 inches by 1440 inches.}\\ \\ B=2880\cdot 1440\\ =4147200\\ \text{Therefore the area of the basilica is 4,147,200 square inches.}\\ \\ T=23\cdot 12 =276 \text{Therefore, the area of each tile is 276 square inches.}\\ \\ N=\frac{4147200}{276}\\ \approx 15026.09\\ \text{Therefore, 15,027 tiles are needed to cover the entire basilica.}\\ \end{array}[/latex]
3.11
1.1
2.1
A wine cellar is 100 feet long and 64 feet wide. How many casks can it hold, given that each cask is seven feet long and four feet wide, and given that there is an aisle four feet wide down the middle of the cellar?
Let [latex]\begin{array}{l}W=\end{array}[/latex] the area of the wine cellar.
Let [latex]\begin{array}{l}A=\end{array}[/latex] the area of the aisle in the cellar.
Let [latex]\begin{array}{l}S=\end{array}[/latex] the area of the storage area of the wine cellar.
Let [latex]\begin{array}{l}C=\end{array}[/latex] the area of each cask.
Let [latex]\begin{array}{l}N=\end{array}[/latex] the number of casks that can be stored in this cellar.
[latex]\begin{array}{l}W=100\cdot 64\\ =6400\\ \\ A=100\cdot 4\\ =400\\ \\ S=W-A\\ =6400-400\\ =6000\\ \\ C=7*4\\ =28\\ \\ N=\frac{S}{C}\\ =\frac{6000}{28}\\ =\frac{1500}{7}\\ \approx 214.29\\ \end{array}[/latex]
Because we cannot store a fraction of a cask, we can store a maximum of 214 casks.
3.12
1.1
2.1
A four-sided town measures 1100 feet on one side and 1000 feet on the other side; on one edge, 600, and on the other edge, 600. I want to cover it with roofs of houses, each of which is to be 40 feet long and 30 feet wide. How many dwellings can I make there?
https://www.geogebra.org/calculator/tmdr4ej4
Because this shape has two sides of equal length and two sides of unequal length, we know that the two side of unequal length must be parallel so as to intersect the two sides of equal length.

[latex]\begin{array}{l}\text{Area of trapezoid}=\frac{x+y}{2}c\dot h\end{array}[/latex]
We can solve for [latex]\begin{array}{l}h\end{array}[/latex] by using Pythagorean Theorem.
The base of the triangle, [latex]\begin{array}{l}x\end{array}[/latex], is half of the difference between the two horizontal lines.
[latex]\begin{array}{l}a=\frac{y-x}{2}\\ =\frac{1100-1000}{2}\\ =\frac{100}{2}\\ =50\\ \\ a^2+b^2=c^2\\ 50^2+h^2=600^2\\ h^2=600^2-50^2\\ h=\sqrt{357500}\\ h=50\cdot\sqrt{143}\\ h\approx 597.91\\ \\ \text{Area of trapezoid}=\frac{x+y}{2}\cdot h\\ =\frac{1000+1100}{2}\cdot 50\cdot\sqrt{143}\\ =\frac{2100}{2}\cdot 50\cdot\sqrt{143}\\ =1050\cdot 50\cdot\sqrt{143}\\ =52500\cdot\sqrt{143}\\ \approx 627808.69\\ \\ \text{Therefore the area of the town is }52,500\cdot\sqrt{143}\text{ sqft.}\\ \\ \text{Area of each house }=40\cdot 30\\ =1200\text{ sqft}\\ \\ \text{Number of houses}=\frac{\text{Area of town}}{\text{Area of each house}}\\ =\frac{52500\cdot\sqrt{143}}{1200}\\ =\frac{175\cdot\sqrt{143}}{4}\\ \approx 523.17\\ \end{array}[/latex]
Therefore 523 houses of dimensions 40ft by 30ft can be made in this town.
3.13
1.1
2.1
I have a cloak 100 cubits long and 80 cubits wide. I wish to make small cloaks with it; each small cloak is 5 cubits long, and 4 wide. How many small cloaks can I make? (1 cubit = 50 cm)
[latex]\begin{array}{l}\text{Area of large cloak}=100\cdot 80\\ =8000\text{ square cubits}\\ \\ \text{Area of each small cloak}=5\cdot 4\\ =20\text{ square cubits}\\ \\ \text{Number of small cloaks}=\frac{\text{Area of large cloak}{Area of each small cloak}\\ =\frac{8000}{20}\\ =400\\ \end{array}[/latex]
Therefore we can make 400 small cloaks.
3.14
1.1
2.1
A four-sided field measures 30 perches down one side and 32 down the other; it is 34 perches across the top and 32 across the bottom. How many acres are included in this field? (1 perch ≈ 5 m. 1 acre = 40 perches by 4 perches ≈ 4000 m[latex]\begin{array}{l}^2\end{array}[/latex])
https://www.geogebra.org/calculator/d4du8dv9
Note that this is not necessarily a trapezoid – there is no indication that any sides are parallel. However, there are multiple solutions if we treat this as any irregular quadrilateral. Therefore, I have to make an assumption to be able to solve.
(If Trapezoid: )
(If we made the top and bottom parallel: https://www.geogebra.org/calculator/cwyuhfmc)
(If we made the sides parallel: https://www.geogebra.org/calculator/uzwzpt7d)
I am assuming that this is a cyclic quadrilateral (has all 4 vertices lying on a circle) and therefore will use Brahmagupta’s formula for a cyclic quadrilateral: [latex]\begin{array}{l}A=\sqrt{(s-a)(s-b)(s-c)(s-d)}\\ \text{Where }s\text{ the semi-perimeter of the quadrilateral }=\frac{a+b+c+d}{2}\\ A\text{ is the area, and }a,\ b,\ c,\text{ and }d\text{ are side lengths of the quadrilateral.}\\ \\ a=30\\ b=34\\ c=32\\ d=32\\ \\ s=\frac{a+b+c+d}{2}\\ =\frac{30+34+32+32}{2}\\ =64\\ \\ A=\sqrt{(s-a)(s-b)(s-c)(s-d)}\\ =\sqrt{(64-30)(64-34)(64-32)(64-32)}\\ =\sqrt{1044480}\\ =64\cdot\sqrt{255}\\ \approx 1022.00\text{ square perches}\\ \\ 1\text{ acre}=40\text{ perches by }4\text{ perches}=160\text{ square perches}\\ \\ \frac{64\cdot\sqrt{255}\text{ square perches}}{160\text{ square perches per acre}}\\ =\frac{2\cdot\sqrt{255}}{5}\\ \approx 6.39 \end{array}[/latex]
Therefore there are approximately 6.39 acres on this field.
3.15
1.1
2.1
There is a triangular city which has one side of 1000 feet, another side of 1000 feet, and a third of 900 feet. Inside of this city, I want to build houses each of which is 20 feet in length and 10 feet in width. How many houses can I build in the city?
This is an Isosceles Triangle as two sides are the same length.
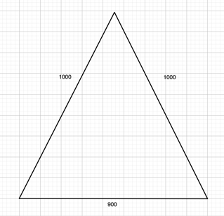
To solve this problem, I will first set design assumptions, and then use a data program to solve the model.
In this city, I imagine one road running North to South, and then rows of houses on either side of the street. There will be horizontal streets separating the front doors of houses, but they will all share back and side walls.
The main, vertical road should be the width of 2 horse-drawn buggies: approximately 8 feet.
Each side road can be the width of 1 horse-drawn buggy: approximately 4 feet.
Starting with the base, we cannot fit houses in the vertical road, nor can we fit rectangular houses in neither the first nor last 10 feet of the row given the angles of the space. Therefore, the amount of useable space on each side of the triangle is:
(900/2)-(8/2)-10
=450-4-10
=436 feet
At 20 feet per house:
436/20
=21.8
Therefore we can fit 21 houses on each side of the road along the base; 42 houses along the base of our city.
The next row of houses will be above these 42, 10 feet wide houses with an additional 4 feet street inbetween.
We know that the base is 900, but its height is not explicitly stated. The height of this triangle can be determined using Pythagorean Theorem. The height is a vertical line going through the top point through the middle of the base. Therefore, the base of this right-angle triangle is half of the base of the full triangle.
[latex]\begin{array}{l}a^2+b^2=c^2\\ (\frac{900}{2})^2+h^2=1000^2\\ h^2=1000^2-450^2\\ \sqrt(h^2)=\sqrt{797500}\\ h=\sqrt{797500}\\ h=50\cdot\sqrt{319}\\ h\approx 893.03\\ \\ \text{Therefore the height of the triangle is approximately 893.03 feet.}\\ \end{array}[/latex]
Moving upwards by 14 feet, the next row of houses start at a height of 879 feet. Similarly to the previous row, we cannot fit houses in the first 10 feet of the base due to the angle of the edge of the city, nor in the 4 feet of one side’s vertical road. Therefore, the amount of base we are working with is 450 ft less the difference due to the change in height (but not the actual height value), less the 10 feet that is on an angle, less the 4 feet for the vertical road. To determine the change in base, we can use the ratio of the base to the height as a fixed ratio and use the known change in height to determine the change in base.
Using an Excel Spreadsheet, I can continue this pattern through the entire triangle and determine that, based on my design assumptions, 1554 rectangular houses can fit within this area.
3.16
1.1
2.1
A little rectangular canal is to be excavated for a length of 5 km. Its width is 2 m, and its depth is 1 m. Each laborer is assigned to remove 4m[latex]\begin{array}{l}^3\end{array}[/latex] of earth, for which he will be paid one-third of a basket of barley. How many laborers are required for the job, and what are the total wages to be paid?
The section being excavated is of dimensions 5000 m by 2 m by 1 m.
The volume of earth being excavated is: [latex]\begin{array}{l}5000\cdot 2\cdot 1\\ =10000\ m^3\\ =10\ km^3\\ \\ \text{Total number of laborers needed}=\frac{\text{total volume of earth to be excavated}}{\text{ volume assigned to each laborer}}\\ =\frac{10000m^3}{4m^3\text{ per laborer}}\\ =2500\text{ laborers}\\ \text{Therefore 2,500 laborers are needed for this job.}\\ \\ \text{Total wages}=\text{Wage per laborer}\cdot\text{Number of laborers}\\ =\frac{1}{3}\cdot 2500\\ =\frac{2500}{3}\\ =833\frac{1}{3}\\ \\ \text{Therefore, }833\frac{1}{3}\text{ baskets of barley will be the total wages paid for this job.} \end{array}\\[/latex]
3.17
1.1
2.1
A canal is 5 rods long, 11/2 rods wide, and 1/2 rod deep. Workers are assigned to dig 10 gin of earth for which task they are paid 6 sila of grain. What is the area of the surface of this canal and its volume? What are the number of workers required and their wages? (1 rod = 12 cubits = 12 x 50 cm= 6 m, 1 sar area = 36 m[latex]\begin{array}{l}^2\end{array}[/latex], 1 gin = 5 litres, 1 sila = 1 litre ]
[latex]\begin{array}{l}\text{Given: }1\text{ rod}=12\text{ cubits}=6\ m\\ \text{Therefore: }5\text{ rods}=60\text{ cubits}=30\ m\text{ (multiply everything by 5)}\\ \frac{11}{2}\text{ rods}=66\text{ cubits}=33\ m\\ \frac{1}{2}\text{ rod}=6\text{ cubits}=3\ m\\ \\ \text{Volume of dig site}=30\ m\cdot 33\ m\cdot 3\ m\\ =\frac{55}{4}\text{ cube rods}\\ =2970\ m^3\\ \text{Therefore the volume is }2970\ m^3// \\ \text{Surface Area}=(4\text{ sides}\cdot\text{area of each side})+(2\text{ ends}\cdot\text{area of each end})\\ =4\cdot (30\cdot 33)+2\cdot (33\cdot 3)\\ =4\cdot 990+2\cdot 99\\ =4158\ m^2\\ \text{Therefore the surface area is }4158\ m^2\\ \\ \text{Given: }1\text{ gin}=5\text{ litres}=5\text{ sila}\\ \text{Note: }1000\text{ litre}=1\text{ cubic metres}\\ \text{Therefore: }10\text{ gin}=50\text{ litres}=50\text{ sila} =\frac{1}{20}\text{ cubic metres (divide by 1000)}\\ \\ \text{Number of workers}=\frac{\text{total volume of dig site}}{\text{volume per worker}}\\ =\frac{2970}{\frac{1}{20}}\\ = 59400\\ \text{Therefore 59,400 workers are to be hired for this job.}\\ \\ \text{Total wages}=\text{wage per worker}\cdot\text{number of workers}\\ =6\cdot 59400\\ =356400\\ \end{array}[/latex]
Therefore 356,400 sila, which is 356,400 litres or 71,280 gin of grain, is needed for total wages.
3.18
1.1
2.1
A siege ramp is to be built to attack a walled city. The volume of earth allowed is 5400 sar. The ramp will have a width of 6 rods, a base length of 40 rods, and a height of 45 cubits. Construction of the ramp is incomplete; an 8-rod gap is left between the end of the ramp and the city wall. The height of the uncompleted ramp is 36 cubits. How much more earth is needed to complete this ramp? (1 sar volume = 1 sar area x 1 cubit =18 m[latex]\begin{array}{l}^3\end{array}[/latex] , 1 cubit = 50 cm; 1 rod = 12 cubits = 6 m.)
Total ramp dimensions:
– Max 5400 sar of earth
– Length = 40 rods
– Width = 6 rods
– Height = 45 cubits
Given: 1 rod = 12 cubits
Let [latex]\begin{array}{l}h=\end{array}[/latex] the height of the ramp in rods.
[latex]\begin{array}{l}h\text{ rods}:45\text{ cubits}\\ h=\frac{45}{12}\text{ rods}\\ \\ \text{Volume of ramp}=\frac{40\cdot 6\cdot\frac{45}{12}}{2}\\ =\frac{900}{2}\\ =450\text{ cubic rods}\\ \end{array}[/latex]
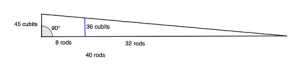
Note: 36 cubits = 3 rods
[latex]\begin{array}{l}\text{Volume of amount completed}=\frac{(40-8)\cdot 3\cdot 6}{2}\\ =\frac{576}{2}\\ =288\\ \end{array}[/latex]
Therefore 288 cubic rods of earth have been completed.
[latex]\begin{array}{l}\text{Amount remaining}=\text{Total}-\text{Amount completed}\\ =450-288\\ =162\\ \end{array}[/latex]
Therefore 162 cubic rods of earth left.
To measure this in sar of earth, we first converts the rods to metres.
Given: 1 rod = 6 m.
[latex]\begin{array}{l}1\text{ cubic rod}=6\ m\cdot 6\ m\cdot 6\ m=216\ m^3\\ \text{volume of earth in }m^3:\\ 162\text{ cubic rods}\cdot 216\text{ cubic metres per rod}\\ =34992\\ \end{array}[/latex]
Therefore there are 34,992 cubic metres of earth needed to complete this ramp.
Given: 1 sar volume = 18 cubic metres.
[latex]\begin{array}{l}\text{volume in sar}=\frac{34992}{18}\\ =1944\text{ sar}\\ \end{array}[/latex]
Therefore 1944 sar of earth is needed to complete the ramp.
Chapter 5 – Pythagorean Theorem
5.1
1.1
2.1
In the center of a river whose width is 10 chi grows a reed whose top reaches 1 chi above the water level. If we pull the reed towards the bank, its top is even with the water’s surface. What is the depth of the river?
Let’s set up a model showing the reed with height h that, when growing vertically, extends 1 above the water. Therefore the depth of the river is equal to h – 1.
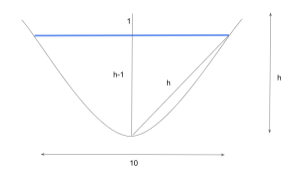
Since the width of the river is 10, the width of half the river is 5. Therefore, we are solving a Pythagorean triangle with side lengths 5 and h-1, and hypotenuse h
[latex]\begin{array}{l}5^2+\left(h-1\right)^2=h^2\\ 5^2+h^2-2h+1=h^2\\ 25+h^2-2h+1=h^2\\ 25-2h+1=0\\ 26=2h\\ h=13\end{array}[/latex]
Therefore, the depth, or h-1, equals 12 chi.
5.2
1.1
2.1
Given a pyramid 300 cubits high, with the square base 500 cubits on a side, determine the distance from the center of any side to the apex.
Given a pyramid 300 cubits high, with a square base 500 cubits on a side, determine the distance from the centre of any side to the apex

When we consider a vertical cross-section of the pyramid that intersects with the top vertex, we notice that it is an isosceles triangle with base of 500 cubits and height of 300 cubits. If we draw a height line down from the top vertex, we have a line that bisects the base, creating 2 congruent right triangles with base 250 cubits and height 300 cubits.
The point at which the cross-section intersects the edge of the base is the centre of the side. Therefore, the distance being asked is the hypotenuse of the right triangles in the diagram below:

[latex]\begin{array}{l}a^2+b^2=hyp^2\\ 250^2+300^2=hyp^2\\ 62500+90000=hyp^2\\ hyp^2=152500\\ hyp=\sqrt{152500}=50\sqrt{61}\approx390.5125\end{array}[/latex]
Therefore, the distance from the centre of each side to the apex is approximately 390.5125 cubits.
5.3
1.1
2.1
A pyramid has a base of 360 cubits and a height of 250 cubits. What is its seqt (the ratio of vertical and horizontal dimensions)?
The ratio of vertical and horizontal dimensions or seqt is [latex]250/(360/2)=25/18[/latex]
5.4
1.1
2.1
Find the height of a square pyramid with a seqt (the ratio of vertical and horizontal dimensions) of 21 fingers per cubit (cubit equals 28 fingers) and a base of 140 cubits on one side. Find the length of the slope.
The seqt or the ratio of vertical and horizontal dimensions is [latex]21/28=3/4[/latex]
Thus if the horizontal distance is [latex](140/2)=70[/latex] cubits then the vertical is [latex]70/4×3=52.5[/latex] cubits or 52 cubits 14 fingers.
You can calculate the slope by two methods:
1) Since the legs of the right triangle in the diagram are in 3 to 4 ratio then the hypotenuse is in 5 to 4 to 3 ratio (a Pythagorean triplet). The length of the slope is [latex]70/4×5=87.5[/latex] cubits or 87 cubits and 14 fingers
2) By the Pythagorean theorem the length of the slope is a square root of [latex]70^2+52.5^2=87.5[/latex]

5.5
1.1
2.1
A rectangular plot is 60 cubit square; the diagonal is 13 cubits. How many cubits does it take to make the sides?
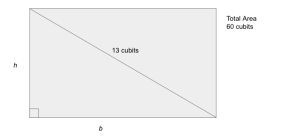
You can solve the problem by three methods.
Method 1. One of the Pythagorean triples is 5, 12, 13. Thus the sides are 5 and 12 cubits.
Method 2. Quadratic equation,
Since we know that d = 13 and A = 60
[latex]\begin{array}{l}bh=60\\ b=\frac{60}{h}\\ \therefore13=\left(\frac{60}{h}\right)^2\end{array}By\ substitution:\begin{array}{l}13^2=b^2+h^2\\ 13^2=\left(\frac{60}{h}\right)^2+h^2\\ 169=\frac{3600}{h^2}+h^2\\ 169h^2=3600+h^4\\ h^4-169h^2+3600=0\\ \left(h^2\right)^2-169\left(h^2\right)+3600=0\end{array}Use\ Quadratic\ Formula\ with\ h^2\ as\ the\ variable:\begin{array}{l}h^2=\frac{169\pm\sqrt{\left(-169\right)^2-4\left(3600\right)}}{2}\\ \ \ =\frac{169\pm\sqrt{28561-14400}}{2}\\ \ \ =\frac{169\pm\sqrt{14161}}{2}\\ \ \ =\frac{169\pm119}{2}\\ h^2=144\ or\ 25\\ h=\pm12\ or\ \pm5\end{array}[/latex]
Since the side lengths must be positive values, these values must be 12 cubits and 5 cubits respectively.
Method 3. Trial and error
Students may try a trial and error with different side lengths that result in an area of 60, as laid out in the following table (as well as the opposite order):
[latex]\begin{array}{l}1\times60=60,\ d\approx60.01&&4\times15=60,\ d\approx15.52\\ 2\times30=60,\ d\approx30.07&&5\times12=60,\ d=13\\ 3\times20=60,\ d\approx20.22&&6\times10=60,\ d\approx11.66\end{array}[/latex]
5.6
1.1
2.1
An erect pole of 10 cubits has its base moved 6 cubits. Determine the new height and the distance the top of the pole is lowered.
An erect pole, 10 cubits in length, has its base moved outwards, 6 cubits. Determine the new height and the distance the top of the pole has been lowered.
Consider that the original height is the length of the pole, or 10 cubits. With this consideration, we can model the problem:
Animation:
Diagram:
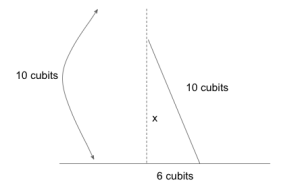
Method 1 – Pythagorean theorem
The hypotenuse (the pole) is known. Therefore:
[latex]\begin{array}{l}x^2+6^2=10^2\\ x=\sqrt{10^2-6^2}\\ x=\sqrt{100-36}\\ x=\sqrt{64}\\ x=8\end{array}[/latex]
Method 2 – Pythagorean triples
The lengths of the sides form a Pythagorean Triple 6-8-10. The two sides are 6 and 10 (with 10 as the hypotenuse), therefore the missing side is 8 cubits.
5.7
1.1
2.1
There is a hole at the foot of a pillar 9 hastas high, and a pet peacock standing on top of it. Seeing a snake returning to its hole at a distance from the pillar equal to three times its height, the peacock swoops down upon the snake slantwise. Say quickly, how far from the pole does the meeting of their paths occur?
Let the peacock and snake meet at x m from the pillar as shown in the above figure.
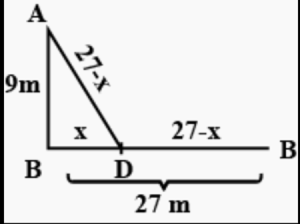
Again we can solve the question by the Pythagorean triples. In this case it is 9, 12, 15 triple. So the peacock and snake are going to meet at a distance of 12 feet from the pillar. Or we can write and solve the quadratic equation.
5.8
1.1
2.1
A fish is resting at the northeast corner of a rectangular pool. A heron standing at the northwest corner spies the fish. When the fish sees the heron looking at him, he quickly swims towards the south. When he reaches the south side of the pool, he has the unwelcome surprise of meeting the heron who has calmly walked due south along the side and turned at the southwest corner of the pool and proceeded due east, to arrive simultaneously with the fish on the south side. Given that the pool measures 12 units by 6 units, and that the heron walks as quickly as the fish swims, find the distance the fish swam.
We begin by drawing out a model. There are two possible orientations for the 12×6 pool, one in which the 12-unit length is oriented North-South and the second that is oriented east-west. We will call these Scenario 1 and Scenario 2, respectively. These are indicated below:

In all cases:
f is the distance travelled by the fish and h is the distance travelled by the heron
h can be separated into the southbound portion (labelled s) and the eastbound portion (labelled e). Therefore h = f = s + e.
SCENARIO 1
\begin{array}{l}f^2=12^2+\left(6-e\right)^2\\
h=s+e=12+e\\
Since\ h=f,\ then\ f=h=12+e\\
Substituting:\\
\left(12+e\right)^2=12^2+\left(6-e\right)^2\\
144+24e+e^2=144+36-2e+e^2\\
24e=36-2e\\
26e=36\\
e=\frac{36}{26}=1\ \frac{10}{26}=1\ \frac{5}{13}\\
f=12+e\\
f=12+1\ \frac{5}{13}\\
f=13\frac{5}{13}\end{array}
Therefore, each animal travelled [latex]13\frac{5}{13}[/latex] units
SCENARIO 2
\begin{array}{l}f^2=6^2+\left(12-e\right)^2\\
h=s+e=12+e\\
Since\ h=f,\ then\ f=h=12+e\\
Substituting:\\
\left(12+e\right)^2=6^2+\left(12-e\right)^2\\
144+24e+e^2=36+144-24e+e^2\\
24e=36-24e\\
48e=36\\
e=\frac{36}{48}=\frac{3}{4}\\
h=12+e\\
h=12+\frac{3}{4}\\
h=12\frac{3}{4}\end{array}
Therefore, each animal travelled [latex]12\frac{3}{4}[/latex] units.
5.9
1.1
2.1
One monkey came down a tree of height 100 and went to a pond a distance of 200. Another monkey, leaping some distance above the tree, went diagonally to the same place. If their total distances traveled are equal, tell me quickly, learned one —if you have a thorough understanding of calculation- how much is the height of the leap?
Let h be the height of the leap above the tree. Since the diagonal length of the leap is equal to the height of the tree plus the ground distance (100+200), which is 300 units. Therefore, the model looks like:
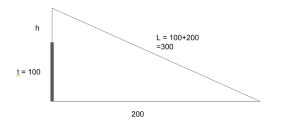
This creates a right triangle with side lengths 200, 300 and h + 100
[latex]\begin{array}{l}\left(h+100\right)^2+200^2=300^2\\ \left(h+100\right)^2+40000=90000\\ \left(h+100\right)^2=50000\\ h+100=\sqrt{50000}\\ h=\sqrt{50000}-100\approx123.6\end{array}[/latex]
Therefore, the height of the jump is approximately 123.6
5.10
1.1
2.1
In a certain lake swarming with red geese, the tip of a lotus bud was seen to extend a span [9 inches] above the surface of the water. Forced by the wind, it gradually advanced and was submerged at a distance of 2 cubits [40 inches]. Compute quickly, mathematician, the depth of the pond.
Let d be the depth of the river. Assuming that the lotus is rooted in a consistent place in the riverbed, then the length of the stem is d+9.
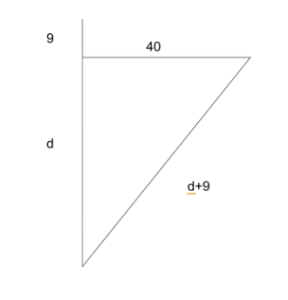
[latex]\begin{array}{l}d^2+40^2=\left(d+9\right)^2\\ 40^2=\left(d+9\right)^2-d^2\\ 1600=d^2+18d+81-d^2\\ 1600=18d+81\\ 1600-81=18d\\ 1519=18d\\ 84.3\overline{8}=d\end{array}[/latex]
5.11
1.1
2.1
Two towers, the heights of which are 30 paces and 40 paces, have a 50 paces distance. Between the two towers there is a font where two birds, flying down from the two towers at the same speed will arrive at the same time. What is the distance of the font from the two towers?
Let d be the distance that each bird flies. If the speed is the same, and the time of departure and arrival is the same, then the distance must also be the same.
Let t be the distance of the font from the thirty-pace tower.
Let f be the distance of the font from the forty-pace tower.
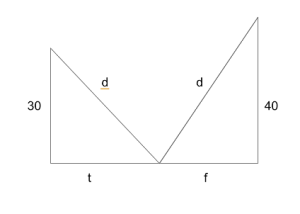
Using the Pythagorean Theorem, and the given information that the towers are 50 paces apart:
[latex]\begin{array}{l}t^2+30^2=d^2\\ f^2+40^2=d^2\\ t+f=50\end{array} \begin{array}{l}f=50-t\\ Substitute:\\ t^2+30^2=d^2\\ \left(50-t\right)^2+40^2=d^2\\ Substituting\ again:\\ t^2+30^2=\left(50-t\right)^2+40^2\\ t^2+900=2500-100t+t^2+1600\\ 900=2500-100t+1600\\ 100t=2500+1600-900\\ 100t=3200\\ t=32\end{array}[/latex]
Therefore, the font is 32 paces from the thirty-pace tower and 50-32 or 18 paces from the 40-pace tower.
Chapter 6 – Ratio and Proportion
6.1
1.1
2.1
The Egyptian pyramids have different slopes. Some pyramids are more high-pitched, others are more low-pitched. Egyptians expressed the steepness of a pyramid by a measure they called “seked”. For instance, they say that a pyramid has to have a seqed of 5 palms 1 finger. What does it mean? First, we have to remember that a cubit, the Egyptian unit of length which is approximately 50 cm, is divided in 28 fingers and each 4 fingers make a palm. So 5 palms 1 finger is 5×4+1= 21 fingers. BTW, can you calculate what is 1 finger in cm?
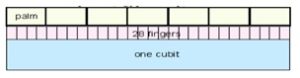
Now for the seqed of 5 palms 1 finger: It means that when you build a pyramid you have to add for each cubit of its height the length of 5 palms 1 finger to each side of its base. if you build a pyramid 1 cubit tall which is 28 fingers the base should be 5 palms 1 finger wide from each side of its centre. A pyramid of 2 cubits high had to be 10 palms 2 fingers wide from each side of its centre.
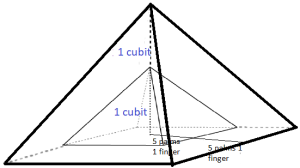
How to calculate the seqed of a pyramid that is already built? To calculate the seqed of a pyramid you have to divide the half of its base by its height. For example, the pyramid below is 250 cubits high. Its base is 360 cubits long. The seqed is 180 divide by 250 which is 0.72. It means that for each cubit of its height the length of 0.72 is added to both sides of its base. But the ancient Egyptians didn’t have decimals so they expressed 0.72 of cubit as fingers. 0.72×1 cubit = 0.72×28 = 20.16 or approximately 20 fingers or 5 palms (remember 1 palm = 4 fingers) and 16/100 or 4/25 of finger.
6.1 a) If a pyramid is 280 cubits high and the side of its base 360 cubits long, what is its seked ?
We are given: To calculate the seqed of a pyramid you divide the half of its base by its height.
Let [latex]\begin{array}{l}S=\end{array}[/latex] the seked of the pyramid.
Let [latex]\begin{array}{l}B=\end{array}[/latex] the base of the pyramid in cubits.
Let [latex]\begin{array}{l}H=\end{array}[/latex] the height of the pyramid in cubits.
[latex]\begin{array}{l}S=\frac{\frac{1}{2}\cdot B}{H}\\ =\frac{\frac{1}{2}\cdot 360}{280}\\ =\frac{180}{280}\\ =\frac{9}{14}\\ \approx 0.64286\text{ of a cubit}\\ \end{array}[/latex]
Except the ancient Egyptians didn’t have decimals, so they would express it in terms of palms and fingers:
[latex]\begin{array}{l}\frac{9}{14}\text{ of a cubit}\\ =\frac{9}{14}\text{ of a cubit}\cdot 28\frac{\text{fingers}}{\text{cubit}}\\ =18\text{ fingers}\\ \text{Remembering that there are 4 fingers per palm:}\\ =\frac{18\text{ fingers}}{4\frac{\text{fingers}}{\text{palm}}}\\ =4\frac{1}{2}\text{ palms}\\ =4\text{ palms and }2\text{ fingers}\\ \end{array}[/latex]
Therefore, the seked of this pyramid is 4 palms and 2 fingers.
6.1 b) If the seked of a pyramid is 5 palms 1 finger per cubit and the side of its base 12 cubits long, what is its altitude?
Let [latex]\begin{array}{l}S=\end{array}[/latex] the seked of the pyramid.
Let [latex]\begin{array}{l}B=\end{array}[/latex] the base of the pyramid in cubits.
Let [latex]\begin{array}{l}H=\end{array}[/latex] the height of the pyramid in cubits.
[latex]\begin{array}{l}S=5\text{ palms }+ 1\text{ finger}\\ =5\text{ palms }\cdot 4\frac{\text{fingers}}{\text{palm}}+1\text{ finger}\\ =20\text{ fingers}+1\text{ finger}\\ =21\text{ fingers}\\ =\frac{21\text{ fingers}}{28\frac{\text{fingers}}{\text{cubit}}}\\ =\frac{3}{4}\text{ of a cubit}\\ =0.75\text{ of a cubit}\\ \\ S=\frac{\frac{1}{2}\cdot B}{H}\\ \frac{3}{4}=\frac{\frac{1}{2}\cdot 12}{H}\\ \frac{3}{4}=\frac{6}{H}\\ \frac{3}{4}\cdot H=6\\ H=6\cdot\frac{4}{3}\\ H=8\\ \end{array}[/latex]
Therefore, the height (or altitude) of this pyramid is 8 cubits.
6.1 c) If the seked of a pyramid is 5 palms 1 finger per cubit and the side of its base 140 cubits, what is its altitude?
Let [latex]\begin{array}{l}S=\end{array}[/latex] the seked of the pyramid.
Let [latex]\begin{array}{l}B=\end{array}[/latex] the base of the pyramid in cubits.
Let [latex]\begin{array}{l}H=\end{array}[/latex] the height of the pyramid in cubits.
[latex]\begin{array}{l}S=5\text{ palms }+ 1\text{ finger}\\ =5\text{ palms }\cdot 4\frac{\text{fingers}}{\text{palm}}+1\text{ finger}\\ =20\text{ fingers}+1\text{ finger}\\ =21\text{ fingers}\\ =\frac{21\text{ fingers}}{28\frac{\text{fingers}}{\text{cubit}}}\\ =\frac{3}{4}\text{ of a cubit}\\ =0.75\text{ of a cubit}\\ \end{array}[/latex]
6.2
1.1
2.1
In ancient Egypt the quality of products made with grain, such as bread and beer, was measured by a unit called a pefsu. Pefsu shows how many loaves of bread or jugs of beer were made from 1 hekat, which is 5 litres, of grain. The more beer or bread you made from the same amount of grain the weaker and less tasty was your beer or bread.. For example, if you make 20 loafs of bread from 1 hekat the bread is of 20 pefsu value. But if you make 40 loaves of bread your bread is of 40 pefsu value. So, the higher the pefsu, the less valuable bread or beer was. If you had one loaf of bread of pefsu 20 you could exchange it to two loaves of pefsu 40 or to three loaves of pefsu 60.
6.2 a) 100 loaves of pesu 10 are to be exchanged for a certain number of loaves of pesu 45. What is the number?
We know that the number will be greater than 100 as loaves of a higher pefsu are worth less, and therefore would require more quantity to be of equal value. We will use this observation to help confirm that our response makes sense given the provided context.
[latex]\begin{array}{|c|c|} \hline\ \text{Pefsu Value} & \text{Number of Loaves}\\ \hline 20 & 1\\ \hline 40 & 2\\ \hline 60 & 3\\ \hline \end{array}[/latex]
We will refer to ratios in terms of Quantity to Pefsu Value; note that the ratio can be reversed (Pefsu Value:Quantity).
Given the ratio of [latex]\begin{array}{l}1:20\end{array}[/latex], it is easy to see how we double both sides to get to the equivalent ratio of [latex]\begin{array}{l}2:40\end{array}[/latex]. Likewise, we triple the original ratio of [latex]\begin{array}{l}1:20\end{array}[/latex] to get the ratio of [latex]\begin{array}{l}3:60\end{array}[/latex].
Given the ratio of [latex]\begin{array}{l}100:10\end{array}[/latex], we can find the ratio [latex]\begin{array}{l}x:45\end{array}[/latex] – where [latex]\begin{array}{l}x\end{array}[/latex] is the number of loaves of pefsu 45 that can be exchanged for 100 loaves of pefsu 10.
To go from a pefsu value of 10 to 45, we multiply 10 by a factor of 4.5. Therefore, to go from a quantity of 100 to x, we multiply 100 by the same factor of 4.5 and we get [latex]\begin{array}{l}x=450\end{array}[/latex].
Therefore, we can exchange 100 loaves of pefsu 10 for 450 loaves of pefsu 45.
6.2 b) 1000 loaves of pefsu 5 are to be exchanged, a half for loaves of pefsu 10, and a half for loaves of pefsu 20. How many of each will there be?
We are given the ratio of [latex]\begin{array}{l}1000:5\end{array}[/latex] representing 1000 loaves of pefsu 5.
Half of the 1000 loaves will be exchanged for loaves of pefsu 10, and the other half for loaves of pefsu 20. Half of 1000 loaves is 500 loaves.
Let [latex]\begin{array}{l}y=\end{array}[/latex] the number of loaves of pefsu 10 from exchanging 500 loaves of pefsu 5.
Let [latex]\begin{array}{l}z=\end{array}[/latex] the number of loaves of pefsu 20 from exchanging 500 loaves of pefsu 5.
We have (i) [latex]\begin{array}{l}500:5\end{array}[/latex] to be exchanged for [latex]\begin{array}{l}y:10\end{array}[/latex]
and (ii) [latex]\begin{array}{l}500:5\end{array}[/latex] is to be exchanged for [latex]\begin{array}{l}z:20\end{array}[/latex]
(i) [latex]\begin{array}{l}500:5=y:10\end{array}[/latex]
To go from a pefsu value of 5 to 10, we multiply 5 by a factor of 2. Therefore, to go from a quantity of 500 to [latex]\begin{array}{l}y\end{array}[/latex], we multiply 500 by the same factor of 2.
[latex]\begin{array}{l}500\cdot 2=y\\ 500\cdot 2=1000\\ \text{Therefore, }500:5=1000:10\\ \end{array}[/latex]
Therefore, 500 loaves of pefsu 5 can be exchanged for 1000 loaves of pefsu 10.
(ii) [latex]\begin{array}{l}500:5=z:20\end{array}[/latex]
To go from a pefsu value of 5 to 20, we multiply 5 by 4. Therefore, to go from 500 to [latex]\begin{array}{l}z\end{array}[/latex], we multiply 500 by the same factor: 4.
[latex]\begin{array}{l}500\cdot 4 = z\\ 500\cdot 4=2000\\ \text{Therefore, }500:5=2000:20\\ \end{array}[/latex]
Therefore, 500 loaves of pefsu 5 can be exchanged for 2000 loaves of pefsu 20.
6.2 c) 1000 loaves of pefsu 10 are to be exchanged for a number of loaves of pefsu 20 and the same number of pefsu 30. How many of each kind will there be?
We want the same number of loaves of pefsu 20 and pefsu 30.
Let [latex]\begin{array}{l}z=\end{array}[/latex] the number of loaves of each pefsu (20 and 30) being exchanged for a total of 1000 loaves of pefsu 10.
[latex]\begin{array}{l}1000:10=a:20+a:30\end{array}[/latex]
We can rewrite the ratios as fractions, and substitute the arrow with an equal sign.
[latex]\begin{array}{l}\frac{1000}{10}=\frac{a}{20}+\frac{a}{30}\\ 100=\frac{30}{30}\cdot\frac{a}{20}\ +\ \frac{20}{20}\cdot\frac{a}{30}\\ 100=\frac{30\cdot a}{30\cdot 20}+\frac{20\cdot a}{20\cdot 30}\\ 100=\frac{30a+20a}{20\cdot 30}\\ 100=\frac{50a}{600}\\ 100=\frac{5a}{60}\\ 100=\frac{a}{12}\\ 100\cdot 12=a\\ 1200=a\\ \text{Therefore, }1000:10=1200:20+1200:30\\ \end{array}[/latex]
Therefore we will be exchanging 1000 loaves of pefsu 10 for 1200 loaves of pefsu 20 and 1200 loaves of pefsu 30.
6.2 d) Suppose it is said to thee, 100 loaves of pefsu 10 are to be exchanged for a quantity of beer of pefsu 2. How many des of beer will there be?
Note: there will be less than 100 beers of pefsu 2 as the higher quality beer will be more valuable than the loaves of bread and therefore will require less quantity to be of equal value.
Let [latex]\begin{array}{l}b=\end{array}[/latex] the number of beers of pefsu 2 being exchanged for 100 loaves of pefsu 10.
[latex]\begin{array}{l}100:10 = b:2\\ \frac{100}{10}=\frac{b}{2}\\ 10=\frac{b}{2}\\ 20=b\\ \text{Therefore, }100:10=20:2\\ \end{array}[/latex]
Therefore 100 loaves of pefsu 10 can be exchanged for 20 des of beer of pefsu 2.
6.2 e) 3[latex]\begin{array}{l}\frac{1}{2}\end{array}[/latex] hekat of grain is made into 80 loaves of bread. Let me know the amount of grain in each loaf and what is the pefsu.
We are given the information that 80 loaves of bread are made from 3[latex]\begin{array}{l}\frac{1}{2}\end{array}[/latex] hekat of grain, and we want to determine the equivalent proportion of hekat of grain per loaf of bread.
Let [latex]\begin{array}{l}x=\end{array}[/latex] the amount of grain in hekat in each loaf of bread.
[latex]\begin{array}{l}80:3\frac{1}{2}=1:x\\ \frac{80}{3\frac{1}{2}}=\frac{1}{x}\\ x=\frac{3\frac{1}{2}}{80}\\ x\approx 0.04375\\ \text{Therefore, }80:3\frac{1}{2}\approx 1:0.04375\\ \end{array}[/latex]
Therefore 0.04375 hekat of grain is used per loaf of bread.
To determine the pefsu value, we again refer back to the information provided: we know that the pefsu value is that amount of beer or loaves of bread made from 1 hekat of grain. In this case, we are talking about loaves of bread.
We know 3[latex]\begin{array}{l}\frac{1}{2}\end{array}[/latex] hekat of grain was used to make 80 loaves. We need to know the number of loaves made per hekat of grain used.
Let [latex]\begin{array}{l}y=\end{array}[/latex] the number of loaves made per hekat of grain used.
[latex]\begin{array}{l}80:3\frac{1}{2}=y:1\\ \frac{80}{3\frac{1}{2}}=\frac{y}{1}\\ 22\frac{6}{7}=y\\ \text{Therefore, }80:3\frac{1}{2}=22\frac{6}{7}:1\\ \end{array}[/latex]
Therefore, 22[latex]\begin{array}{l}\frac{6}{7}\end{array}[/latex] loaves were made per hekat of grain used.
As the pefsu value is the amount of loaves made per hekat of grain used, we have determined that the pefsu value is 22[latex]\begin{array}{l}\frac{6}{7}\end{array}[/latex].
6.3
1.1
2.1
If it is said to you, “Have sailcloth made for the ships,” and it is further said, “Allow 1000 cloth cubits for one sail and have the ratio of the height of the sail to its width be 1 to 1 1/2,” what is the height of the sail?
The area of a triangle is:
[latex]\begin{array}{l}A=\frac{b\cdot h}{2}\\ \text{And the ratio of the height to its width (base) be }1:1\frac{1}{2}\\ h:b=1:1\frac{1}{2}\\ \frac{b}{h}=\frac{1\frac{1}{2}}{1}\\ \frac{b}{h}=1\frac{1}{2}\\ b=1\frac{1}{2}\cdot h\\ \\ A=1000\text{ and }A=\frac{b\cdot h}{2}\\ 1000=\frac{(1\frac{1}{2}\cdot h)\cdot h}{2}\\ 1000=\frac{\frac{3}{2}\cdot h^2}{2}\\ 1000=\frac{3}{4}\cdot h^2\\ 1000\cdot\frac{4}{3}=h^2\\ \frac{4000}{3}=h^2\\ \sqrt{\frac{4000}{3}}=h\\ 20\sqrt{\frac{10}{3}}=h\\ h \approx 36.51484 \end{array}[/latex]
Therefore, the height of the triangular sailcloth is approximately 36.51 cubits.
6.4
1.1
2.1
A cobbler can cut leather for ten pairs of shoes in one day. He can finish five pairs of shoes in one day. How many pairs of shoes can he both cut and finish in one day?
Let [latex]\begin{array}{l}C=\end{array}[/latex] the time it takes a cobbler to cut a pair of shoes.
Let [latex]\begin{array}{l}F=\end{array}[/latex] the time it takes a cobbler to finish a pair of shoes.
[latex]\begin{array}{l}C:F=10:5\\ 10:5=2:1\\ C:F=2:1\\ \end{array}[/latex]
The cobbler can cut twice as many pairs of shoes as they can finish in the same time span.
Using Bar Models, we can express the work that would fill the cobbler’s day the follow ways:
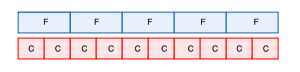
We can assume that the cobbler would need to first cut and then finish a shoe, repeatedly:
![]()
We can count the number of pairs of shoes that are both cut and finished within the time span of a day:
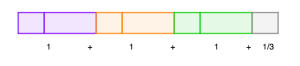
Therefore, in a day, the cobbler can both cut and finish [latex]\begin{array}{l}3\frac{1}{3}\end{array}[/latex] pairs of shoes.
Algebraically, we can express a day’s worth of work in terms of cutting and finishing a pair of shoes:
Let [latex]\begin{array}{l}D=\end{array}[/latex] a day’s worth of work.
Let [latex]\begin{array}{l}p=\end{array}[/latex] the pairs of shoes a cobbler can both cut and finish in a day.
Three (3) ways to express a day’s worth of work are:
[latex]\begin{array}{l}\text{(i) }D=10\cdot C\\ \text{(ii) }D=5\cdot F\\ \text{(iii) }D=p\cdot (C+F)\\ \end{array}[/latex]
Using (i) and (ii):
[latex]\begin{array}{l}10\cdot C=5\cdot F\\ 2\cdot C=F\\ \end{array}[/latex]
Substituting into (iii):
[latex]\begin{array}{l}10\cdot C=p\cdot (C+F)\\ 10\cdot C=p\cdot (C+2\cdot C)\\ 10\cdot C=p\cdot (3\cdot C)\\ 10\cdot C=p\cdot 3\cdot C\\ \text{Divide both sides by C:}\\ 10=3\cdot p\\ \frac{10}{3}=p\\ p=3\frac{1}{3}\\ \end{array}[/latex]
Therefore, the cobbler can cut and finish 3 1/3 pairs of shoes per day.
6.5
1.1
2.1
A fox, a raccoon, and a hound pass through customs and together pay 111 coins. The hound says to the raccoon, and the raccoon says to the fox, “Since your fur is worth twice as much as mine, then the tax you pay should be twice as much!” How much should each pay?
Let [latex]\begin{array}{l}f=\end{array}[/latex] the number of coins that the fox should pay.
Let [latex]\begin{array}{l}r=\end{array}[/latex] the number of coins that the raccoon should pay.
Let [latex]\begin{array}{l}h=\end{array}[/latex] the number of coins that the hound should pay.
We are given:
(i) [latex]\begin{array}{l}f+r+h = 111\end{array}[/latex] The total number of coins being paid by the group is 111.
(ii) [latex]\begin{array}{l}2h = r\end{array}[/latex] The raccoon should pay twice as much as the hound.
(iii) [latex]\begin{array}{l}2r = f\end{array}[/latex] The fox should pay twice as much as the raccoon.
Substituting (iii) into (i) and (ii):
[latex]\begin{array}{l} f+r+h=111\\ 2r+r+h=111\\ 2(2h)+2h+h=111\\ 4h+2h+h=111\\ 7h=111\\ h=\frac{111}{7}\\ r=2h\\ =2\cdot\frac{111}{7}\\ =\frac{222}{7}\\ f=2r\\ =2\cdot\frac{222}{7}\\ =\frac{444}{7}\\ \end{array}[/latex]
Therefore, the fox should pay [latex]\begin{array}{l}\frac{444}{7}\end{array}[/latex] coins, the raccoon should pay [latex]\begin{array}{l}\frac{222}{7}\end{array}[/latex] coins, and the raccoon should pay [latex]\begin{array}{l}\frac{111}{7}\end{array}[/latex] coins.
6.6
1.1
2.1
A cow, a horse, and a goat were in a wheat field and ate some stalks of wheat. Damages of five baskets of grain were asked by the wheat field’s owner. If the goat ate one-half the number of stalks as the horse, and the horse ate one-half of what was eaten by the cow, how much should be paid by the owners of the goat, horse, and cow, respectively?
Let [latex]\begin{array}{l}C=\end{array}[/latex] the amount of wheat stalks eaten by the cow.
Let [latex]\begin{array}{l}H=\end{array}[/latex] the amount of wheat stalks eaten by the horse.
Let [latex]\begin{array}{l}G=\end{array}[/latex] the amount of wheat stalks eaten by the goat.
Given:
[latex]\begin{array}{l}\text{(i) }G=\frac{1}{2}\cdot H\\ \text{(ii) }H=\frac{1}{2}\cdot C\\ \text{(iii) }G+H+C=5\\ \end{array}[/latex]
We can use equations (i) and (ii) to substitute the variables in (iii) to be one variable, and thus solvable.
[latex]\begin{array}{l} G=\frac{1}{2}\cdot H\\ G=\frac{1}{2}\cdot (\frac{1}{2}\cdot C)\\ G= \frac{1}{4}\cdot C\\ \\ G+H+C=5\\ (\frac{1}{4}\cdot C)+(\frac{1}{2}\cdot C)+C=5\\ \frac{1}{4}\cdot C+\frac{1}{2}\cdot C+C=5\\ \frac{7}{4}\cdot C=5\\ C=\frac{5}{\frac{7}{4}}\\ C=\frac{5\cdot 4}{7}\\ C=\frac{20}{7}\\ C=2\frac{6}{7}\\ \\ H=\frac{1}{2}\cdot C\\ H=\frac{1}{2}\cdot\frac{20}{7}\\ H=\frac{20}{14}\\ H= \frac{10}{7}\\ H=1\frac{3}{7}\\ \\ G=\frac{1}{4}\cdot C\\ G=\frac{1}{4}\cdot\frac{20}{7}\\ G=\frac{20}{28}\\ G=\frac{5}{7}\\ \end{array}[/latex]
Therefore the cow’s owner should pay 2[latex]\begin{array}{l}\frac{6}{7}\end{array}[/latex] baskets, the horse’s owner should pay 1[latex]\begin{array}{l}\frac{3}{7}\end{array}[/latex] baskets, and the goat’s owner should pay [latex]\begin{array}{l}\frac{5}{7}\end{array}[/latex] baskets.
6.7
1.1
2.1
If in one day, a person can make 30 arrows or fletch (put the feathers on) 20 arrows, how many arrows can this person both make and fletch in a day?
Let [latex]\begin{array}{l}D=\end{array}[/latex] the time available for this person to work in a day.
Let [latex]\begin{array}{l}A=\end{array}[/latex] the time it takes for this person to make one arrow.
Let [latex]\begin{array}{l}F=\end{array}[/latex] the time it takes for this person to fletch one arrow.
Let [latex]\begin{array}{l}p=\end{array}[/latex] the number of arrows this person can make and fletch in a day.
Given:
[latex]\begin{array}{l}\text{(i) }D=30\cdot A\\ \text{(ii) } D=20\cdot F\\ \text{(iii) } D=p(A+F)\\ \\ \text{Equate (i) and (ii):}\\ 30\cdot A=20\cdot F\\ A=\frac{20\cdot F}{30}\\ A=\frac{20}{30}\cdot F\\ A=\frac{2}{3}\cdot F\\ \\ \text{Substitute into (iii): }\\ D=p(A+F)\\ 20\cdot F=p(\frac{2}{3}\cdot F + F)\\ 20\cdot F=p(\frac{5}{3}\cdot F)\\ 20\cdot F=p\cdot\frac{5}{3}\cdot F\\ \text{Divide both sides by F}\\ 20=\frac{5}{3}\cdot p\\ \frac{3}{5}\cdot 20=p\\ 12=p\\ \end{array}[/latex]
Therefore, this person can make and fletch 12 arrows in a day.
Using Bar Models, we can express the work that would fill this person’s day the follow ways:

We can assume that person would first make an arrow and then fletch it, repeatedly, and then count the number arrows that can be made and fletched within a day’s time span.

And we get the same answer: this person can make and fletch 12 arrows in a day.
6.8
1.1
2.1
In general, a fair exchange is 50 bushels of millet for 27 bushels of rice. Here is 21 bushels of millet. How many bushels of rice will we obtain in exchange?
The value of 50 bushels of millet is equal to 27 bushels of rice.
We want to know the value of 21 bushels of millet in terms of bushels of rice.
As there is to be a consistent exchange ratio between millet and rice, we know that the ratio of [latex]\begin{array}{l}50:27\end{array}[/latex] will have the same proportionality of [latex]\begin{array}{l}21:x\end{array}[/latex], where [latex]\begin{array}{l}x\end{array}[/latex] is the value of 21 bushels of millet in terms of bushels of rice, and is what is to be solved.
[latex]\begin{array}{l}50:27=21:x\\ \frac{50}{27}=\frac{21}{x}\\ x\cdot\frac{50}{27}=21\\ x=21\cdot \frac{27}{50}\\ x=\frac{567}{50}\\ x=11 \frac{17}{50}\\ \text{Therefore, the ratio of 50:27 is proportional to the ratio of 21:11}\frac{17}{50}\\ \end{array}[/latex]
Therefore, 21 bushels of millet can be exchanged for 11[latex]\begin{array}{l}\frac{17}{50}\end{array}[/latex] bushels of rice.
6.9
1.1
2.1
Four counties are required to furnish wagons to transport grain to a depot. There are 10,000 families in the first county, 9500 families in the second county; 12,350 families in the third county; and 12,200 families in the last county. The total number of wagons required is 1000. How many wagons are to be provided by each county according to the size of the population?
Let [latex]\begin{array}{l}A=\end{array}[/latex] the number of wagons to be provided by the first county.
Let [latex]\begin{array}{l}B=\end{array}[/latex] the number of wagons to be provided by the second county.
Let [latex]\begin{array}{l}C=\end{array}[/latex] the number of wagons to be provided by the third county.
Let [latex]\begin{array}{l}D=\end{array}[/latex] the number of wagons to be provided by the fourth county.
[latex]\begin{array}{l}A+B+C+D=1000\\ \\ \text{The total number of people living across all 4 counties are:}\\ 10,000 + 9,500 + 12,350 + 12,200 = 44,050\\ \end{array}[/latex]
[latex]\begin{array}{|c|c|c|} \hline\ \text{County} & \text{Number of Families} & \text{Proportion of Total Population}\\ \hline 1 & 10,000 & \frac{10,000}{44,050}=\frac{200}{881}\\ \hline 2 & 9500 & \frac{9500}{44,050}=\frac{190}{881}\\ \hline 3 & 12,350 & \frac{12,350}{44,050}=\frac{247}{881}\\ \hline 4 & 12,200 & \frac{12,200}{44,050}=\frac{244}{881}\\ \hline \end{array}[/latex]
Each County’s Proportion of Total Population can be used as the same factor to determine the proportion of wagons each county is to provide:
[latex]\begin{array}{l}A=\frac{200}{881}\cdot 1000\\ A\approx 227\\ B=\frac{190}{881}\cdot 1000\\ B\approx 216\\ C=\frac{247}{881}\cdot 1000\\ C\approx 280\\ D=\frac{244}{881}\cdot 1000\\ D\approx 277\\ \end{array}[/latex]
Therefore, the first county should supply 227 wagons, the second county should supply 216 wagons, the third county should supply 280 wagons, and the fourth county should supply 277 wagons for a total of 1000 wagons, according to the size of their population.
6.10
1.1
2.1
A man had four creditors. To the first he owed 624 ducats; to the second, 546; to the third, 492; and to the fourth, 368. It happened that the man defaulted and escaped, and the creditors found that his goods amounted to 830 ducats in all. In what ratio should they divide this, and what will be the share of each?
Let [latex]\begin{array}{l}A=\end{array}[/latex] ducats to be shared to the first creditor.
Let [latex]\begin{array}{l}B=\end{array}[/latex] ducats to be shared to the second creditor.
Let [latex]\begin{array}{l}C=\end{array}[/latex] ducats to be shared to the third creditor.
Let [latex]\begin{array}{l}D=\end{array}[/latex] ducats to be shared to the fourth creditor.
[latex]\begin{array}{l}A+B+C+D=830\\ \\ \text{The total amount owed across all 4 creditors are:}\\ 624 + 546 + 492 + 368 = 2030\\ \end{array}[/latex]
[latex]\begin{array}{|c|c|c|} \hline\ \text{Creditor} & \text{Amount Owed} & \text{Proportion of Total Owed}\\ \hline 1 & 624 & \frac{624}{2030}=\frac{312}{1015}\\ \hline 2 & 546 & \frac{546}{2030}=\frac{39}{145}\\ \hline 3 & 492 & \frac{492}{2030}=\frac{246}{1015}\\ \hline 4 & 368 & \frac{368}{2030}=\frac{184}{1015}\\ \hline \end{array}[/latex]
Each creditor’s Proportion of Total Owed can be used as the same factor to determine the proportion of ducats each creditor should collect:
[latex]\begin{array}{l}A=\frac{312}{1015}\cdot 830\\ A\approx 255.133\\ B=\frac{39}{145}\cdot 830\\ B\approx 223.241\\ C=\frac{246}{1015}\cdot 830\\ C\approx 201.163\\ D=\frac{184}{1015}\cdot 830\\ D\approx 150.463\\ \end{array}[/latex]
If we were to round all the values, the total value would sum to 829 ducats. Therefore, we look at the decimals and see that the fourth creditor is closest to the next largest whole number and should be awarded the remaining ducat.
Therefore, the first creditor should be given 255 ducats, the second creditor should be given 223 ducats, the third creditor should be given 201 ducats, and the fourth creditor should be given 151 ducats for a total of 830 ducats, as proportional to the amount owing to each creditor.
6.11
1.1
2.1
There were two men, of whom the first had three small loaves of bread and the other two. They walked to a spring, where they sat down and ate; and a soldier joined them and shared the meal, each of the three men eating the same amount. When all the bread was eaten, the soldier departed, leaving 5 bezants to pay for his meal. The first man accepted 3 of these bezants, since he had three loaves; the other took the remaining 2 bezants for his two loaves. Was this division fair?
The three men ate an equal share of 5 loaves of bread.
They each ate [latex]\begin{array}{l}\frac{5}{3}\end{array}[/latex] loaves.
5 loaves = [latex]\begin{array}{l}\frac{15}{3}\end{array}[/latex] loaves.
The first man brought 3 loaves.
3 loaves = [latex]\begin{array}{l}\frac{9}{3}\end{array}[/latex] loaves.
The second man brought 2 loaves.
2 loaves = [latex]\begin{array}{l}\frac{6}{3}\end{array}[/latex] loaves.
So the first man brought enough for himself, and ([latex]\begin{array}{l}\frac{9}{3}\end{array}[/latex] – [latex]\begin{array}{l}\frac{5}{3}\end{array}[/latex] = [latex]\begin{array}{l}\frac{4}{3}\end{array}[/latex]) nearly enough for Ali.
The 2nd man brought enough for himself, and ([latex]\begin{array}{l}\frac{6}{3}\end{array}[/latex] – [latex]\begin{array}{l}\frac{5}{3}\end{array}[/latex] = [latex]\begin{array}{l}\frac{1}{3}\end{array}[/latex]) [latex]\begin{array}{l}\frac{1}{3}\end{array}[/latex] to Ali.
So first man gave up [latex]\begin{array}{l}\frac{4}{3}\end{array}[/latex]
Second man gave up [latex]\begin{array}{l}\frac{1}{3}\end{array}[/latex]
Of the bread given to Ali, the first man supplied [latex]\begin{array}{l}\frac{\frac{4}{3}}{\frac{5}{3}} = \frac{4}{5}\end{array}[/latex]
Of the bread given to Ali, the second man supplied [latex]\begin{array}{l}\frac{\frac{1}{3}}{\frac{5}{3}}=\frac{1}{5}\end{array}[/latex]
Therefore, this division of bezants is not fair. Instead, of the 5 bezants, 4 should go to the first man and 1 should go to the second man.
6.12
1.1
2.1
Suppose I tell you that I bought saffron in Siena for 18 lire a pound and took it to Venice, where I found that 10 ounces Siena weight are equivalent to 12 ounces in Venice, and 10 lire in Siena money are equal to 8 lire Venetian. I sell the saffron for 14 lire Venetian money a pound. I ask how much I gained in percent.
Note: there are 16 ounces (oz) in a pound (lb).
10 oz Siena weight : 12 oz Venice weight
10 lire Siena money : 8 lire Venetian money
Saffron sells for 18 lire/lb in Siena
= 18 lire for 16 oz (Siena weight)
Saffron sells for 14 lire/lb in Venice
= 14 lire for 16 oz (Venice weight)
Converting 1 lb Siena weight to Venice weight:
Recall: 10 oz Siena weight = 12 oz Venice weight
1 oz Siena weight = [latex]\begin{array}{l}\frac{12}{10}\end{array}[/latex] oz Venice weight
Therefore, to go from Siena weight to Venice weight, we multiply by a factor of [latex]\begin{array}{l}\frac{12}{10}\end{array}[/latex] = 1.2
1 lb (16 oz) in Siena weight would be:
16 oz in Siena weight [latex]\begin{array}{l}\cdot 1.2 = 19.2\end{array}[/latex] oz in Venice weight
Therefore, 18 lire Siena money buys 19.2 ounces Venice weight.
Converting 18 lire Siena money to Venetian money:
10 lire Siena money = 8 lire Venetian money
1 lire Siena money = [latex]\begin{array}{l}\frac{8}{10}\end{array}[/latex] lire Venetian money
Therefore, to go from Siena money to Venetian money, we multiple by a factor of [latex]\begin{array}{l}\frac{8}{10}\end{array}[/latex]=0.8
18 lire Siena [latex]\begin{array}{l}\cdot 0.8 = 14.4\end{array}[/latex] lire Venetian
Therefore, 14.4 lire Venetian money buys 19.2 ounces Venice weight.
Determining the equivalent exchange rate for 1 lb (16 oz) Venice weight:
Given: 14.4 lire per 19.2 oz Venice weight
Want: how much lire per 16 oz Venice weight?
Let x = the amount of lire for 16 oz Venice weight
[latex]\begin{array}{l}\frac{14.4}{19.2} = \frac{x}{16}\\ 16\cdot\frac{14.4}{19.2} = x\\ 12 = x\end{array}[/latex]
Therefore, 12 lire Venetian money buys 1 lb (16 oz) Venice weight.
Calculate the percentage gain:
The saffron was sold for 14 lire Venetian money per pound (16 oz Venice weight).
Therefore, the additional profit was (14 – 12 = ) 2 lire Venetian money per lb.
Percentage gain:
[latex]\begin{array}{l}\frac{2}{12}\cdot 100\% \\ =\frac{1}{6}\cdot 100\% \\ =0.16667\cdot 100\% \\ \approx 16.667\% \\ \end{array}[/latex]
Therefore, you gained approximately 16.67% on the saffron transaction.
6.13
1.1
2.1
6.14
1.1
2.1
6.15
1.1
2.1
6.16
1.1
2.1
6.17
1.1
2.1
6.18
1.1
2.1
6.19
1.1
2.1
6.20
1.1
2.1
