Chapter 2 – Circles
Map
1.1
1.19
Timeline
1.1
1.19
Introduction
The circle is a basic shape and a simple plane figure. But, it is a mysterious shape. There is something fantastical about the circle that we perceive on a subconscious level. Circular shapes are foundational geometrical creations of the universe that instill a sense of order, safety, and beauty upon all who observe them.
The importance of circles to human cultures is highlighted in many places, but also in some you might not expect, like language. When we refer to our close friends, we say “circle of friends.” The word encyclopedia comes from ancient Greek words for “circle of learning.” Even the fundamental nature of reality demands our attention to circular patterns. For example, if a group of people speak with each other, they are inclined to be face to face in a circle, not a line, or a polygon, or a rectangle. In sacred Indigenous ceremonies, talking circles were typically used to create a structure where each person’s voice is given equal importance.
Most of the early settlements, villages, and cities have followed circular arrangements. Coliseums, circuses, theaters, concert halls, stadiums, and even many present-day and ancient cities and settlements use circles as a blueprint for their design. Try to visualize how a circular layout of homes could forge a strong sense of unity for its inhabitants, as well as serve as protection against danger from all directions. Such circular planning was applied in ancient cities like Arkaim in the Southern Urals of Russia, the round city of Darabgerd in Iran, or Teuchitlan in Mexico. Many modern cities also use the same design in the form of a ring-shaped road encircling them; Paris, Berlin, Brussels, Addis Ababa, Lahore, Hyderabad, and Melbourne, to name a few.
If we journey back 11,000 years into prehistory, we yet again witness the importance of circular shapes in architecture.
Pre-ancient inhabitants of what is now Turkey erected a superstructure of massive stone carvings arranged in circles. Despite having not yet developed writing, agriculture, metal tools or pottery, they were nonetheless fixated on demonstrating their inherent desire to replicate the beauty and symmetry of the circle.
What is the reason humans are so fascinated by circles and not squares, rhombuses, and other shapes? Are we drawn to seek out symmetries created by the universe? And, if so, why? Researchers theorize three possible explanations. First, angular shapes like thorns, teeth, and jagged rocks, present threats to our safety, whereas round shapes elicit a sense of safety. Secondly, human beings showcase happy emotions in a curvilinear way – arcing smiles, rounded cheeks. Thirdly, our eyes see the world through a circular frame, and it’s possible we are attracted to aesthetics that blend accordingly with that same shape. Whether it’s supergiant stars, human cells, or subatomic particles like electrons, circular shapes appear throughout the universe on the largest and smallest scales imaginable. And, as a species uniquely appreciative of harmony and transcendence, we are forever mesmerized by their symbolic representation of eternity, continuity, perfection, and unity.
Quest for Pi
From the time immemorial people used a straightedge, be it a modern school ruler or measuring rod of ancient Egypt and Babylon, to measure the length of objects. But it is pretty tricky if not impossible to measure the length of circles by straightedges. The only dimension that can be measured by a straightedge in circles is the radius or its double the diameter. Thus all the known mathematics were trying to find the relationship between the diameter of a circle and the perimeter or circumference. If you know the ratio of the diameter of a circle to its circumference you can measure the diameter and quickly calculate the circumference. But how do you know the circumference of a circle in the first place if you can’t
measure it? Ancient societies were not obsessed with precision, and a good approximation was generally enough for their practical tasks. And what is the best (and easiest) approximation of a circle if not a regular polygon, square, pentagon, hexagon, etc.?
Explore the following problems from different historic sources. What were the values of the ratio C/d that these mathematics used? Which one was the closest to the modern approximation of pi?
Judea – The tumultuous history of the Talmud
As long as there has been human civilization, there has been war. Ancient, medieval, and modern accounts highlight the complete and utter devastation wrought by armed conflict. How is it possible then, that through the ravages of war, the Jewish people were able to strengthen their tradition, and create one of the most quintessential books of their religious faith?
Most religions have a central book that captures the arc of their beliefs and teachings. For the Jewish people, this book is the Talmud. Serving as the architecture for Jewish religious law, the Talmud is a chronicle of debates held by generations of spiritual leaders and teachers called rabbis. In biblical times, these debates were held in the Temple of Jerusalem, focusing on philosophy, law, and how best to interpret the Hebrew Bible. The shocking part is that, back then, none of the debates were recorded – all of the knowledge and wisdom gathered through them was kept alive in the minds of the rabbis, being passed down to further generations only through speech. This is called the oral tradition. For centuries, the system of oral tradition preserved the teachings of the Talmud without any problem. However, trouble was on the horizon.
In 66 AD, the Jewish peoples’ homeland of Judaea was ruled by the Roman empire, more specifically, the Roman procurator Gessius Florus. After receiving less tax money from Judaea than he felt was owed, Gessius Florus ordered his troops to seize silver from the holiest site in the Jewish world: the Temple of Jerusalem. This act ignited explosive opposition to the Romans, to which Gessius Florus responded by massacring thousands of Judaeans. A full-scale rebellion ensued, and while the Romans troops were undeniably strained by the Jewish resistance, their military might proved too strong to fend off. By 70 AD, most of Judaea had been destroyed, and only Jerusalem was still standing.
Under the direction of the Roman general, Titus, a massive army of sixty-thousand soldiers attacked Jerusalem with the sole purpose of razing it to the ground. Despite being greatly outnumbered, the Jewish resistance was able to keep the Roman onslaught at bay for over five months!
The mixture of Jerusalem’s defensive walls and the passionate fighting of the Jewish soldiers made it extremely difficult for the Romans to lay siege to the city. Although they fought courageously, the Roman war machine wore down the Jewish resistance and eventually broke through the walls of the city and burnt Temple. Jerusalem was completely demolished by the ruthless Roman army. Witnesses remarked “that nothing was left that could ever persuade visitors that it had once been a place of habitation.”
Widely regarded as one of the most disastrous events in Jewish history, the destruction of their capital city required the Jewish people to reimagine how they preserved their culture. Facing the uncertainty of having no Temple, no central meeting place for the continued debate of the Talmud, rabbis abandoned their oral tradition and began documenting the teachings of the Talmud in writing. This would ensure its survival should their people ever endure being separated from each other.
The story behind the writing of the Talmud is a lesson in overcoming adversity. It is a window into the strange relationship between destruction and creation, and how sometimes a terrible loss can have a silver lining. As the saying goes, necessity is the mother of invention.
2.1
1.1
2.1
One of the geometric rules given in the Talmud is “How much is the square greater than the inscribed circle? A quarter” What was the Talmudic value for pi?
2.2
1.1
2.2
In 4000 year old Egyptian papyrus we read “A circular field has diameter 9 chet. What is its area?” The Ahmes, the scribe of the papyrus, gives the solution: “Subtract 1/9 of the diameter namely 1 chet. The remainder is 8 chet. Multiply 8 by 8; it makes 64. Therefore, it contains 64 square chet of land.”
For the Egyptians a square with the side length 8/9 of the diameter of a circle was a good enough approximation to calculate the area of a circle.
Calculate the ancient Egyptian value of pi.
2.3
1.1
2.3
In Babylonian mathematics a circle was equated to a regular hexagon which side was equal to the radius of a circle. Calculate the Babylonian value of pi.
Medieval Europe – Schools in the Middle Ages
Reading, writing, and going to school every day is seen by many as more of a chore than a privilege. It’s easy to take these monumental opportunities for granted, especially when we don’t consider what the alternatives are. Imagine how hard it would be to go through life completely illiterate – seeing nothing more than meaningless letters when looking at a sign, or having to ask someone to help you read an email. It sounds crazy, but did you know that for most of human history the average person couldn’t read or write?
In the early Middle Ages, most Europeans weren’t able to read and write… The peasant class was the most likely to be illiterate since all of their time was occupied performing physical labour to provide for their families. However, the trend of illiteracy also extended to the noble classes, and even to most kings! The job of reading and writing fell on the clergymen, the monks and religious figures who worked in the Roman Catholic Church. Since the printing press wasn’t invented until the 15th century, monks spent much of their lives copying ancient texts and manuscripts by hand in order for them to be replicated. As a result, the monasteries where the monks lived boasted incredible libraries, and became centers of education. Many kings sought advice from the educated monks, but the problem was that many monks had taken a vow of seclusion, preventing them from sitting on the king’s council.
Medieval rulers began to understand that having very few educated citizens threatened the stability of their empires. One king in particular had plans to change that: Charlemagne, King of the Franks, ruling from 768-814, held a strong desire to educate his people, and ordered monasteries and cathedrals to offer free education for all young boys. The new schools were established inside cathedrals or large churches. Their main purpose was to teach boys how to read and write in Latin since it was the language of the Holy Roman Empire. 
On top of learning Latin grammar, students were also instructed in the subject of logic (the art of debate), and rhetoric (the art of public speaking). Other studies included music, art, and various forms of physical education such as archery, wrestling, horseshoes, and hammer-throwing. Science and math were also taught, however, they weren’t a priority compared to other subjects.
Now that they had designated schools, subjects, teachers, and students, only one thing was missing – textbooks! King Charlemagne invited a well-known monk from England named Alcuin of York to help design them. Born in 735, Alcuin had become a clergyman, scholar, poet, teacher, and was called “the most learned man anywhere to be found.” So, naturally, he was a perfect fit for the role. Among his numerous works, Alcuin wrote a collection of math puzzles that stood out as one of the earliest math textbooks for kids. Unfortunately, only one of his books survived into modern times, and, amazingly enough, is still used in math classes over a thousand years after his death! The book is a series of fifty-three math problems called “Problems to Sharpen the Young.”
Try to solve one of them.
2.4
1.1
2.4
There is a round field which contains 400 yards in its circumference. How many square yards will its area be? Alcuin obtains 10000 square yards. How does he get that, you might ask? Calculate the value of pi he used.
2.5
1.1
2.5
There is a city which is 8000 feet in circumference. How many houses could the city contain if each house is 30 feet long and 20 feet wide?
Japan – Samurai mathematicians
The samurai were the warriors of Japan. For centuries, the samurai served as military to the daimyos, or “lords” of Japan. Even the word “samurai” roughly translates as “those who serve.”
In 1600, Japan was divided into two alliances: the Western Army, commanded by Toyotomi Hideyoshi and the Eastern Army, led by Tokugawa Ieyasu. Toyotomi and his Western Army, whose soldiers were mostly samurai, invaded Korea with the plan to use Korea as the platform to conquer China.
Meanwhile, Tokugawa kept his forces away from the Korean campaign, and samurai who did not want to fight in Korea and China rallied under him. When the Eastern Army became strong enough it fought against Toyotomi’s army in the Battle of Sekigahara, the largest battle of Japanese feudal history Tokugawa and his Eastern Army won.
This victory marks the beginning of the Tokugawa Shogunate, and the beginning of a period of peace in Japan that lasted almost 300 years. During this period, the war-trained samurai became redundant, their warrior skills were not required. and they had to earn their living by working as clerks or other governmental jobs, But the civil jobs were not as demanding as military service. These jobs left samurai with more leisure time on their hands. Many of samurai discovered that there was a lot more in this world rather than battles and wars. They used their time on other pursuits. They studied literature, philosophy, and mathematics. Turns out that these studies opened samurai doors to earn money in an unexpected for samurai way. The civil jobs were not paid handsomely, the pay was poor. 
And the samurai started taking teaching posts at small private schools called juku, which taught martial arts, of course, but also mathematics. The juku were attended by other samurai, merchants, and farmers. The juku students wanted to be able to solve mathematical problems on their own, some to better calculate business transactions, some to better plan their land and some just for pleasure and entertainment.
And this is the story of how samurai became mathematicians.
2.6
1.1
2.6
A circular road A that is 48 km in circumference touches at point P another circular road B of circumference 36 km. A cow and a horse start walking from the point P along the road A and B, respectively. The cow walks 6 km per day and the horse walks 12 km per day. How many days later days later do the cow and horse meet again at P?
2.7
1.1
2.7
A circle of radius r is inscribed in an isosceles triangle with sides 10 and 12. Find r.
Japan – Sungaku: mathematical offerings to gods and spirits
Can you imagine that mathematical problems are used as offerings to gods? Hard to imagine but there was once a Japanese tradition to draw geometrical problems on wooden tablets and place them as offerings at Shinto shrines or Buddhist temples.
The tradition started after the Battle of Sekigahara in 1600. The Eastern Army under the rule of Tokugawa Ieyasu won and Tokugawa began his rule of Japan.
Tokugawa was deeply concerned over the rise of Christianity and other Western influences on Japanese people brought by the ever-increasing trade. He feared the changes the Western influence might bring on the traditional Japanese values and way of living. And thus he decided to close the country to forbid Portuguese, Spanish and other ships to enter Japan. The whole country went to sort of lockdown for 265 years. This Japan vs. the world lockdown was called sakoku, which means in Japanese “country in chains” or “lock up of country”). During the centuries long sakoku no foreigner could enter or Japanese leave the country on penalty of death.
Interestingly enough, the period of sukoku was one of the most prosperous and productive periods in Japan history. Japan greatly developed many aspects of their culture, including literature, art, and mathematics. Many practices were created and revived during this time, one of which was the practice of hanging wooden tablets, called sangaku, at shrines temples. The sangaku were colorfully painted and inscribed with math problems which, in a Western context, would be like seeing math problems etched on glass windows in a cathedral. While this practice might seem odd and weird, it made perfect sense to the people of that time.
The practice of hanging these wooden tablets could be traced back to the practice of giving offerings to the gods. For instance, the most favorable offering would be a horse, but as most people couldn’t afford to offer a horse, they chose to inscribe drawings of a horse on a wooden tablet as a substitute. The sangaku, a word that literally means “mathematical tablet”, may have been also acts of homage–a thanks to a guiding spirit. Or they may have been cheeky challenges to other worshipers: The sangaku were hung up by various mathematic enthusiasts, including samurai, merchants, farmers; men, women and children alike. They would hang as a challenge to other worshippers, as if saying: “solve this if you can!”.
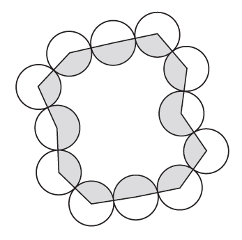
2.8
1.1
2.8
The centers of a loop of the circles of radius r form the vertices of a polygon, as shown in the figure below. Let S1 be the sum of the shaded areas of the circles, and S2 the sum of the unshaded areas of the circles. Find S2 – S1.
