Chapter 6 – Ratio and Proportion
Map
1.1
1.19
Timeline
1.1
1.19
Introduction
Have you ever wondered why humans see some things as beautiful? What would you say to the idea that there was a mathematical formula that influences what we see as beauty? There is, in fact, a secret ratio, and it is called The Golden Ratio.
As you have studied mathematics, you have learned about ratios and proportion. For example, if a ratio of pizzas to celery sticks is 2:5, and there are 20 pizzas, how many celery sticks would there be? 50, right? Perhaps it sounds boring to some, but when we imagine that mathematics is used to decode the fundamental language of the universe, applying it gives us the power to perceive the raw nature of reality in ways we never could before! One of the most interesting uses of ratios and proportions is illuminating our understanding of beauty across the whole of nature. Here’s where the Golden Ratio comes in.
Have you ever wondered why you see a cat’s face as beautiful? How about the pyramids of Egypt, the Taj Mahal, or the Mona Lisa? How would you feel knowing that these seemingly different things share a common mathematical connection? That connection is The Golden Ratio. It is a symmetrical relationship so widespread across nature, art, music, architecture, and even human biology, that it quietly guides our concept of what is and is not beautiful. When applied, it creates a natural, harmonious, and visually pleasant experience to all who observe it.

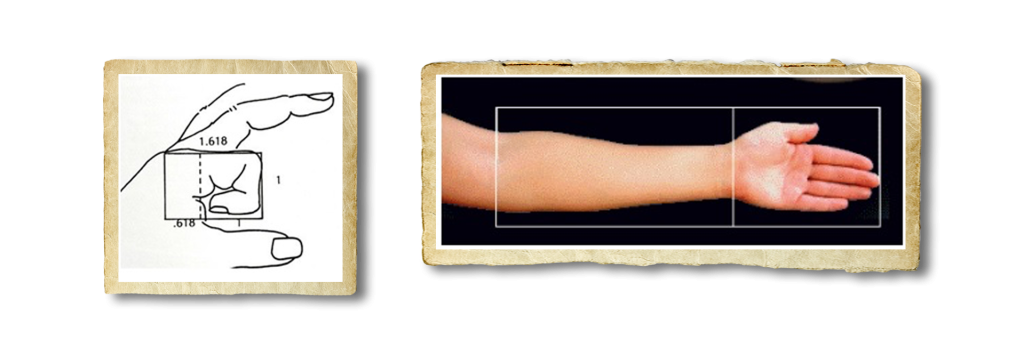
Now, to the fun part – the math. The Golden Ratio is 1:1.68 – aka the length is 1 and width is 1.68. Let’s see how it affects the world right in front of us. Have a look at your index finger. Notice that, from the tip to the base of your wrist, each section is bigger than the last one by a ratio of 1 to 1.68. Using this scale, your fingernail is 1 unit in length. The ratio between your hand and your forearm does the same, abiding by the Golden Ratio.
Although beauty is mysterious, and is ultimately in the eye of the beholder, there are basic characteristics of beauty that are inseparable from the Golden Ratio. Rather than being solely established by cultural beliefs, recent science claims that beauty standards have their roots in mathematics. Proportions and ratios are useful in our everyday lives, but they have a secret, and ancient life of their own as cosmic agents of beauty and harmony across the universe.
Pyramids across the World
Humanity’s architectural achievements are truly astonishing. Looking up at the great monuments of the world like the Eiffel Tower or Taj Mahal can have a truly humbling effect on us. But, have you ever wondered why human civilizations build such tall towers? With a new record-breaking tower erected every decade, from Toronto’s CN Tower to the Burj Khalifa in Dubai, there seems to be a never ending competition among mankind to construct taller and taller buildings. Even in the biblical story, The Tower of Babel, the ancient Babylonians built a tower so tall, it was perceived as a threat to God! We know how the builders of today do it, but how did the ancients manage to construct such impressive buildings without the help of modern machinery?

The greatest architectural mystery of the ancient world is by far the Pyramids of Giza. Although the ancient Egyptians are widely known for constructing the most iconic pyramids in the world, they were not the only ancient culture to build them. Archaeological digs have discovered pyramids across the ancient world whether it be in Mesopotamia, China, India, Indonesia, Cambodia, Spain, Italy, Nigeria, and Sudan. Pyramids were even found on the other side of the globe! Mesoamerican cultures like the Incan, Mayan, Aztec, Xelhua, Toltec, Velacruz, and Teotihuacan all excelled at Pyramid building. But, the question remains…how did ancient peoples build such majestic pyramids? What technology did they use?

Since there is no evidence to answer that question, we can only rely on speculation. Was it strictly a matter of hard labor and dedication? Or were they using a technology we are not aware of? Take the pyramids in Chichen Itza in Mexico, for example. The main pyramid, Kukulkan, stands atop a rectangular platform 55.5 metres wide and 24 meters tall, with a 6 metre temple perched atop it. Witnessing the sheer magnitude of these megalithic structures suggests that manpower alone could not have been solely responsible for their construction. With a missing piece to this puzzle, many have foregone modern scientific reasoning and sought to obtain answers from ancestral legends instead.
Ancient Mayan legends claim their pyramids were built with the help of magic powers. The descendants of the Mayans still hold this idea to be true, but with a key insight: the magic powers were not actually magic, but rather, they were a forgotten technology! Can you try and guess what it was? According to locals in the south of the Yucatán Peninsula, their mystery machine wasn’t a machine at all. It was sound! They maintain that the ancient Mayans would whistle in such a way as to harness an extraordinary amount of energy – enough to move megalithic stones! Imagine that scene: gigantic stones and wooden logs floating through the air of a construction site, guided by the whistle of a musical foreman! No hammers, drills, or cranes, just the wonder of enormous objects dancing on the wind to the tune of ancient music.
Whether it’s with modern machinery or with an ancient technology long since forgotten, one thing remains clear: humanity’s ambition to build towering structures will likely never come to an end. But, where our ambition will lead us is yet to be determined. Can you imagine what the skyscrapers of the future will look like?
6.1
1.1
5.1
The Egyptian pyramids have different slopes. Some pyramids are more high-pitched, others are more low-pitched. Egyptians expressed the steepness of a pyramid by a measure they called “seked”. For instance, they say that a pyramid has to have a seqed of 5 palms 1 finger. What does it mean? First, we have to remember that a cubit, the Egyptian unit of length which is approximately 50 cm, is divided in 28 fingers and each 4 fingers make a palm. So 5 palms 1 finger is 5×4+1= 21 fingers. BTW, can you calculate what is 1 finger in cm?
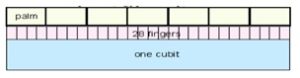
Now for the seqed of 5 palms 1 finger: It means that when you build a pyramid you have to add for each cubit of its height the length of 5 palms 1 finger to each side of its base. if you build a pyramid 1 cubit tall which is 28 fingers the base should be 5 palms 1 finger wide from each side of its centre. A pyramid of 2 cubits high had to be 10 palms 2 fingers wide from each side of its centre.
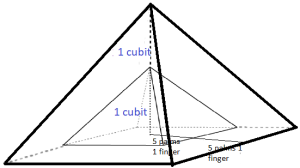
How to calculate the seqed of a pyramid that is already built? To calculate the seqed of a pyramid you have to divide the half of its base by its height. For example, the pyramid below is 250 cubits high. Its base is 360 cubits long. The seqed is 180 divide by 250 which is 0.72. It means that for each cubit of its height the length of 0.72 is added to both sides of its base. But the ancient Egyptians didn’t have decimals so they expressed 0.72 of cubit as fingers. 0.72×1 cubit = 0.72×28 = 20.16 or approximately 20 fingers or 5 palms (remember 1 palm = 4 fingers) and 16/100 or 4/25 of finger.
6.1 a)
If a pyramid is 280 cubits high and the side of its base 360 cubits long, what is its seked?
6.1 b)
If the seked of a pyramid is 5 palms 1 finger per cubit and the side of its base 12 cubits long, what is its altitude?
6.1 c)
If the seked of a pyramid is 5 palms 1 finger per cubit and the side of its base 140 cubits, what is its altitude?
6.2
1.1
5.1
In ancient Egypt the quality of products made with grain, such as bread and beer, was measured by a unit called a pefsu. Pefsu shows how many loaves of bread or jugs of beer were made from 1 hekat, which is 5 litres, of grain. The more beer or bread you made from the same amount of grain the weaker and less tasty was your beer or bread.. For example, if you make 20 loafs of bread from 1 hekat the bread is of 20 pefsu value. But if you make 40 loaves of bread your bread is of 40 pefsu value. So, the higher the pefsu, the less valuable bread or beer was. If you had one loaf of bread of pefsu 20 you could exchange it to two loaves of pefsu 40 or to three loaves of pefsu 60.
6.2 a)
100 loaves of pesu 10 are to be exchanged for a certain number of loaves of pesu 45. What is the number?
6.2 b)
1000 loaves of pefsu 5 are to be exchanged, a half for loaves of pefsu 10, and a half for loaves of pefsu 20. How many of each will there be?
6.2 c)
1000 loaves of pefsu 10 are to be exchanged for a number of loaves of pefsu 20 and the same number of pefsu 30. How many of each kind will there be?
6.2 d)
Suppose it is said to thee, 100 loaves of pefsu 10 are to be exchanged for a quantity of beer of pefsu 2. How many des of beer will there be?
6.2 e)
3 1/2 hekat of grain is made into 80 loaves of bread. Let me know the amount of grain in each loaf and what is the pesu. (pefsu?)
6.3
1.1
5.1
If it is said to you, “Have sailcloth made for the ships,” and it is further said, “Allow 1000 cloth cubits for one sail and have the ratio of the height of the sail to its width be 1 to 1 1/2,” what is the height of the sail?
6.4
1.1
5.1
A cobbler can cut leather for ten pairs of shoes in one day. He can finish five pairs of shoes in one day. How many pairs of shoes can he both cut and finish in one day?
China Terracotta Warriors and the Search For Eternal Life
On March 29th, 1974, a groundbreaking discovery was made in northwestern China. Local peasants digging a well accidentally unearthed fragments of a millennia-old terracotta clay figure. This peculiar finding led archaeologists to excavate the site, revealing an ancient tomb guarded by one of the most significant archaeological discoveries in modern history: the Terracotta Army of China’s first Emperor, Qin Shi Huangdi.
The terracotta clay army consisted of more than 8,000 life-sized soldiers and 600 war-horses in full armor and battle formation. Weighing up to 272 kilograms each (600 pounds), and many standing two meters tall (roughly 6 feet), the soldiers showcased remarkable detail, with each clay sculpture characterized by unique facial features, hairstyles, clothing, and posture. But, who was China’s First Emperor? And, why did he surround himself with the monumental terracotta army?

Born Prince Ying Zheng in the year 259 B.C., he became King of the Qin State at the age of thirteen, and by age twenty-two had turned into the emperor that would revolutionize ancient China in a number of ways: uniting China in 221 B.C. by taking over the six independent kingdoms of the late Warring States Period, creating a single system for writing, units of weight, measurement, and coinage; building the Great Wall to strengthen the northern border, and establishing the Ling Canal to connect China’s north and south river systems.
However, all of these achievements came at a huge cost to the people of ancient China. The Emperor governed with an iron fist. His tyrannical reign was guided by the philosophy of Legalism, which was based on the cynical belief that the average person is motivated by self-interest and, therefore, more likely to do wrong than right. As time passed, the Emperor forbade all other philosophies and ordered the destruction of texts not conforming Legalist views. Anecdotal evidence suggests he may have even executed writers, philosophers, and scholars to stamp out opposing ideologies.
After a career of landmark achievements, China’s first emperor set his sights on one final conquest: death itself! Increasingly obsessed with discovering the proverbial fountain of youth, he sought the advice of his alchemists, who fascinated him with tales of magical life-extending herbs found only on the Islands of the Immortals in the East China Sea – a mystical place that only allowed pure-hearted children to enter. In 219 B.C., emperor Qin Shi Huangdi dispatched thousands of children to the islands. When they never returned, he sent three alchemists. Just one returned, recounting that the islands were protected by an enormous fish, and that their expedition had failed. Unable to accept his mortality, emperor Qin Shi Huangdi journeyed to find the islands himself, but instead of conquering death, he succumbed to it along the way. Experts believe he died from consuming mercury administered by his alchemists, who themselves believed it to be the elixir of life.
At the same time he was searching for immortality, emperor Qin Shi Huangdi was also planning for the afterlife. Throughout his entire life, he had been gradually constructing an enormous underground burial chamber bursting with his empire of riches, and guarded by his army of terracotta warriors, chariots, and war-horses. After conquering the whole of ancient China, he truly believed he could do the same in the great beyond! The question is, would his terracotta soldiers still serve their emperor in the afterlife?
6.5
1.1
A fox, a raccoon, and a hound pass through customs and together pay 111 coins. The hound says to the raccoon, and the raccoon says to the fox, “Since your fur is worth twice as much as mine, then the tax you pay should be twice as much!” How much should each pay?
6.6
1.1
A cow, a horse, and a goat were in a wheat field and ate some stalks of wheat. Damages of five baskets of grain were asked by the wheat field’s owner. If the goat ate one-half the number of stalks as the horse, and the horse ate one-half of what was eaten by the cow, how much should be paid by the owners of the goat, horse, and cow, respectively?
6.7
1.1
If in one day, a person can make 30 arrows or fletch (put the feathers on) 20 arrows, how many arrows can this person both make and fletch in a day?
6.8
1.1
5.5
In general, a fair exchange is 50 bushels of millet for 27 bushels of rice. Here is 21 bushels of millet. How many bushels of rice will we obtain in exchange?
6.9
1.1
5.6
Four counties are required to furnish wagons to transport grain to a depot. There are 10,000 families in the first county, 9500 families in the second county; 12,350 families in the third county; and 12,200 families in the last county. The total number of wagons required is 1000. How many wagons are to be provided by each county according to the size of the population?
Europe Mathematical Duels
Competition is an inherent feature of the human condition and beyond. Whether it’s animals, plants, or microscopic life, every organism on the planet is competing against one another for resources, status, or the highest position in their given hierarchy. It is no wonder then, that sports play such a significant role in human society. Whether it’s MMA, basketball, or even professional video gamers, the need to compete and achieve the triumph of success proliferates through many aspects of our lives and even goes beyond sport and into the realm of science. Renaissance Italy boasted one of the most bizarre forms of competition to date: Mathematical duels…the most famous example of these contests revolved around the discovery of a general solution of cubic equations.
In the early 16th century, an Italian mathematician named Scipione Dal Ferro from the University of Bologna secretly devised a solution to cubic equations: x3+px=n𝑥3+𝑝𝑥=𝑛. A few years after his death, a mathematician from Brescia named Niccolò Pisano, nicknamed Tartaglia, meaning “stammerer,” revealed to the mathematics community that he had discovered a solution to cubic equations, the key to unlocking a seemingly unsolvable, two-thousand-year-old mathematical problem! Determined to undermine Tartaglia’s announcement, a former student of Dal Ferro’s named Antonio Maria Fiore publicly challenged Tartaglia to a mathematical duel!
Modeled after knightly duels, the cartelli di matematica disfida or “bills of mathematical challenge,” consisted of a series of oral or written mathematical equations posed by each competitor to one another with juries, notaries, and witnesses present to observe the battle. As per this challenge, Tartaglia and Fiore provided each other with thirty problems, to be solved in forty days. Tartaglia shocked the community by solving all thirty equations in two hours! Dal Fiore, however, was unable to solve even a single problem.
Four years later, in 1539, Tartaglia disclosed his secret formula as a twenty-five verse poem to Gerolamo Cardano, a Milanese physician and mathematician, swearing him never to reveal it to the outside world. Cardano did, however, allow his student Ludovico Ferrari to see Tartaglia’s formula for third-degree equations, which Ferrari then used as a necessary tool to create a solution for the next frontier in mathematics: fourth-degree equations. Ferrari wanted to publish his momentous discovery, but doing so would reveal Tartaglia’s equation, and feeling honor-bound to Tartaglia, Cardano refused to allow Ferrari to publish the solution to fourth-degree equations.

As fate would have it, Cardano and Ferrari later stumbled upon the work of Scipione Dal Ferro, and were astonished to learn that he in fact had discovered a solution to cubic equations prior to Tartaglia. With this new information, Cardano asserted that his oath of secrecy to Tartaglia was now voided, and he and Ferrari were free to publish their work on fourth-degree equations!
In 1545, Cardano published Ars Magna (the Great Art) which included the formulae for the general solution of equations of the third and fourth degree. Outraged by the betrayal, Tartaglia traveled to Milan to challenge Cardano to a mathematical duel. Perhaps too ashamed to face Tartaglia himself, Cardano skipped town and his student Ferrari filled in for him, squaring off with Tartaglia in front of a large crowd including the Governor of Milan, Don Ferrante Gonzaga. Unfortunately, for Tartaglia, this was not a written duel, but rather, a spoken one which highlighted Tartaglia’s speech impairment. With most of the crowd rooting for Ferrari, Tartaglia was soundly defeated, and humiliated so much so that he later lost his job in Brescia. The solution for cubic equations was then credited to Cardano, and went on to be known as Cardano’s Formulae.
Who would have thought that the world of mathematics could be so deeply entangled with competition, betrayal, and glory? It is a stark reminder that no matter how high the arc of human achievement rises, it is nonetheless subject to, and perhaps driven by, the ever-present pursuit of individual notoriety. Cynical as it may seem, it begs the question, without the desire for personal glory, how many of the achievements that have propelled humanity towards a brighter future would have even come into existence whatsoever?
6.10
1.1
5.7
A man had four creditors. To the first he owed 624 ducats; to the second, 546; to the third, 492; and to the fourth, 368. It happened that the man defaulted and escaped, and the creditors found that his goods amounted to 830 ducats in all. In what ratio should they divide this, and what will be the share of each?
6.11
1.1
5.8
There were two men, of whom the first had three small loaves of bread and the other two. They walked to a spring, where they sat down and ate; and a soldier joined them and shared the meal, each of the three men eating the same amount. When all the bread was eaten, the soldier departed, leaving 5 bezants to pay for his meal. The first man accepted 3 of these bezants, since he had three loaves; the other took the remaining 2 bezants for his two loaves. Was this division fair?
6.12
1.1
5.9
Suppose I tell you that I bought saffron in Siena for 18 lire a pound and took it to Venice, where I found that 10 ounces Siena weight are equivalent to 12 ounces in Venice, and 10 lire in Siena money are equal to 8 lire Venetian. I sell the saffron for 14 lire Venetian money a pound. I ask how much I gained in percent.
6.13
1.1
5.10
Suppose you have two kinds of wine. A measure of the poorer sort is worth 6 denarii. One of the better sort is worth 13 denarii. I wish to have a measure of wine worth 8 denarii. How much of each wine should I put in the mixture?
6.14
1.1
5.8
A dying man makes a will: if the wife gives birth to a male child, she will have one third of what he leaves, his son the other two parts; and if the wife gives birth to a daughter, the wife will receive two thirds and the girl one third. It now happens that the woman bears twins, one male and one female. The question is how much comes to the woman, the male and female child when the legacy values 70 lire.
6.15
1.1
5.9
The head of a household had 20 servants. He ordered them to be given 20 measures of corn as follows. The men must receive three measures, the women must receive two measures, and the children half a measure each. How many men, women and children servants are there in the household?
6.16
1.1
5.10
A head of a household had 100 servants. He ordered that they be given 100 measures of corn as follows. The men should receive three measures, the women should receive two measures, and the children should receive half a measure each. How many men, women, and children servants are there in the household?
6.17
1.1
5.8
A certain bishop ordered 12 loaves of bread to be divided amongst the clergy. He stipulated that each priest should receive two loaves, each deacon should receive half a loaf and each reader should receive a quarter of a loaf. It turned out that the number of clerics and the number of loaves were the same. How many priests, deacons and readers must there have been?
6.18
1.1
5.9
Most of the ratio or proportion problems can be solved by the method called “the rule of three”. The rule of three came to us from medieval India. It was transported to other countries by Arabian voyagers, and, thanks to the Islamic invasion of Spain, the rule made it to Europe. In the 13th century the Italian merchant and mathematician Leonardo de Fibonacci, who frequently traveled to North Africa, learned about the the rule of three and made it popular among European merchants and bankers. Let’s look at the example Fibonacci gives:
If 12 bottles of wine cost 30 denari, what will 42 bottles of wine cost? Fibonacci says, make a square as follows, then multiply the two numbers that lie in the diagonal and then divide by the remaining number: (30 x 42)/12. The result is the price to be paid, 105 denari.
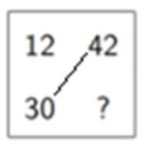
6.18 a)
Suppose 100 rolls of cotton cost 40 lira, how much would five rolls cost?
6.18 b)
I have bought five palas of sandalwood for nine rupakas. How much sandalwood, then, should be obtained for one rupaka?
6.19
1.1
5.10
If 12 horses can plow 96 acres in 6 days, how many horses will plow 64 acres in 8 days?

