Topic 8 Practice Questions

1. Fred Co. is the only producer in the market. The market demand curve and total cost curve are given as: Q = 240 – 0.25P, and TC = 50Q – 0.5Q​². How many units should Fred Co. produce to maximize profit?

(A) 303

(B) 60

(C) 130

(D) 32

 

Correct Answer: C

Steps:

Rewrite the demand function Q = 240 – 0.25P

P = 960 – 4Q

MR = 960 – 8Q

TC = 50Q – 0.5Q²​

MC = ΔTC/ΔQ = 50 – Q

The company maximizes its profit at MR = MC

960 – 8Q = 50 – Q

Solve for Q

Q = 130 units

 

2. Apple Inc. sells AirPods and enjoys monopoly power because no close substitutes are available to consumers. As more brands of wireless earbuds are introduced into the market, the demand for AirPods becomes ________ elastic and the value of the Lerner index ________.

(A) less; decreases

(B) more; decreases

(C) less; increases

(D) more; increases

 

Correct Answer: B

Steps:

As more brands of wireless earbuds are available to consumers, the demand for AirPods becomes more elastic.

The Lerner index of monopoly power = (P – MC)/P = -1/E_d. As Ed increases, the Lerner index decreases.

 

3. Suppose a CD shop is the only seller of music CDs in Hamilton. The demand curve for CDs is given as Q = 300 – 2P. The marginal cost is given as: MC = 10. Find the value of the Lerner index.

Answer: L = 0.875

Steps:

Rewrite Q = 300 – 2P

P = 150 – 1/2Q

MR = 150 – Q

The CD shop maximizes its profit at MR = MC

150 – Q = 10

Q = 140

Substituting Q = 140 into P = 150 – 1/2Q

P = 150 – 1/2 * 140 = 80

The Lerner index = (P – MC)/P = (80 – 10)/80 = 0.875

 

4. Sam’s Oil Shop is the only supplier in the local market. The demand curve is given as: Q = 100 – 5p. Sam has two plants: Plant 1 and Plant 2. The marginal cost of each plant is given as:

MC₁ = 10 + 5Q₁

MC₂ = 15 + 5Q₂

Determine the profit-maximizing output level of each plant.

 

Answer: Q₁ = 1.8, Q₂ = 0.8

Steps:

Rearrange MC₁ and MC₂:

Q₁ = MC₁/5 – 2

Q₂ = MC₂/5 – 3

Sum Q1 and Q2 horizontally

Q = MC₁/5 + MC₂/5 – 5

Replace MC₁ and MC₂ using a common MC

Q = 2MC/5 – 5

MC = (5Q + 25)/2

Rearrange the market demand function

P = 20 – Q/5

MR = ΔTR/ΔQ = 20 – 2Q/5

Set MR = MC

20 – 2Q/5 = (5Q + 25)/2

29Q = 75

Q ≈ 2.59

Substitute Q = 2.59 into MC

We get MC ≈ 18.98

When maximizing profit, MC = MC₁ = MC₂

Substitute MC = 18.98 into Q₁ and Q₂

Q₁ = MC₁/5 – 2 = 18.98/5 – 2 = 1.796 ≈ 1.80

Q₂ = MC₂/5 – 3 = 18.98/5 – 3 = 0.796 ≈ 0.80

 

5. Suppose SolarCar Inc. is the only firm that produces solar-powered cars. Its demand curve, marginal revenue, and marginal cost curve are as follows:

P = 180 – 2Q

MR = 180 – 4Q

MC = 2Q

Assume the market structure was initially perfectly competitive. Changing from perfect competition to monopoly, the change in consumer surplus is _____, and the change in producer surplus is _____. The deadweight loss caused by monopoly power is ______.

(A) -1,125; 675; and 450

(B) 900; 2,700; and -225

(C) 1125; -675; and -450

(D) -900; 2,700; and 225

 

Correct Answer: A

Steps:

 

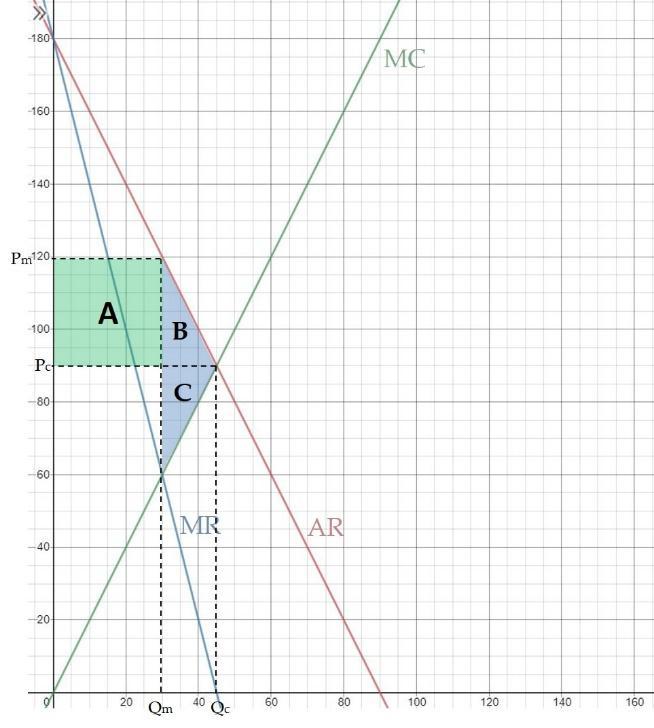
As shown in the graph, changing from perfect competition to monopoly,

ΔCS = -(A + B)

ΔPS = A – C

The deadweight loss is area B and C.

To calculate areas A, B, and C, we need to find Q_c, Q_m, P_c, and P_m.

To find Q_c and P_c,

180 – 2Q = 2Q

Q_c = 45

P_c = 90

To find Q_m and P_m,

MC = MR

180 – 4Q = 2Q

Q_m = 30

P_m = 120

Area A = 30 * (120 – 90) = 900

Area B = 0.5 * (45 – 30) * (120 – 90) = 225

At Q_m = 30, MC = 2 * 30 = 60

Area C = 0.5 * (45 – 30) * (90 – 60) = 225

△CS = -(A + B) = -(900 + 225) = -1,125

△PS = A – C = 900 – 225 = 675

DWL = B + C = 225 + 225 = 450

 

6. A monopolist has a constant marginal cost of $30 per unit of output, and the price elasticity of demand is -3. What is the firm’s profit-maximizing price?

(A) $20

(B) $45

(C) $25

(D) $10

 

Correct Answer: B

Steps:

The monopolist sets MR = MC to maximize profit.

MR = MC = 30

MR = P(1 + 1/E_d)

30 = P(1 + 1/(-3))

Solve for P

P = 45

 

7. Answer the following questions:

(i) A monopolist wants to maximize his profit. Which output option will he choose?

(ii) Assume the monopolist’s objective is to maximize the total revenue. Which output option will he choose then?

(A) The output option where total revenue exceeds total cost.

(B) The output option where marginal revenue equals total cost.

(C) The output option where the slope of the total revenue curve and the slope of the marginal revenue curve are equal.

(D) The output option where the slope of total revenue curve and the slope of the total cost curve are equal.

(E) The output option where marginal revenue hits the horizontal axis.

 

Answer:

(i) D

(ii) E

 

8. A monopolist increases his firm’s output and lowers his firm’s price. As a result, his firm discovers that its total revenue decreases. In this situation, the firm should:

(A) Decrease output as it is producing in the elastic range of its demand curve.

(B) Increase output as it is producing in the elastic range of its cost curve.

(C) Decrease output as it is producing in the inelastic range of its demand curve.

(D) Increase output as it is producing in the inelastic range of its cost curve.

 

Correct Answer: C

Steps:

The fact that total revenue decreases when the price falls indicates that the monopolist is producing in the inelastic range of the demand curve. In this case, marginal revenue is negative. To maximize profit, the monopolist should decrease output.

 

9. Which of the following statements regarding natural monopoly is correct?

(A) Several firms are in this market.

(B) If the government sets price at the level where MC = AR, the firm will incur a loss and eventually go out of business.

(C) Without government intervention, the firm will set the price at MC = MR.

(D) Both B and C.

 

Correct Answer: D

 

10. Suppose a firm is the only computer producer in the local market. The market demand function is given as: Q = 200 – 2P. The firm’s total cost function is given as: TC = 10Q.

The government levies a unit-tax of $10 on computers. What is the profit-maximizing price after the imposition of tax?

(A) $45

(B) $55

(C) $60

(D) $65

 

Correct Answer: C

Steps:

Q = 200 – 2P

Rearrange this equation: P = 100 – 0.5Q

MR = 100 – Q

TC = 10Q

MC = 10

With a unit tax t = 10, the new marginal cost function MC_t is:

MC_t = 10 + t = 10 + 10 = 20

Equate MR and MC to maximize profit

100 – Q = 20

Q = 80

Substituting Q = 80 into the demand function Q = 200 – 2P

Solve for P

P = 60

 

11. Which of the following markets would be best classified as an oligopsony?

(A) The market for apples.

(B) The market for cars.

(C) The market for iPhones.

(D) The market for spaceship engines.

 

Correct Answer: D

Steps:

An oligopsony defines a market with only a few buyers. The market for a highly expensive and specialized product such as spaceship engines would only have a few buyers compared to the other more traditional consumer products listed.

 

12. Barrick Gold Company is the only employer of miners in a remote region of the country. Assume the price of gold decreases, the firm’s employment level ________ and the equilibrium wage ________.

(A) decreases; decreases

(B) decreases; increases

(C) increases; decreases

(D) increases; increases

 

Correct Answer: A

Steps:

If the price of gold decreases, MV will shift down. The labour supply schedule and ME will not change. The company set MV = ME to maximize profit. With a lower MV, both employment level and wage will decrease.

 

13. Consider a monopolist producer. The demand curve and total cost curve are given below:

Q = 180 – 2P

TC = 5Q

Suppose that a tax of $5 for each unit produced is imposed by the government. What is the monopolist’s profit level after the imposition of the unit tax?

(A) $3200

(B) $4000

(C) $3612.5

(D) $3000

 

Correct Answer: A

Steps:

Rearrange Q = 180 – 2P

P = 90 – 1/2Q

TR = 90Q – 1/2Q²

MR = ΔTR/ΔQ = 90 – Q

With the unit tax, TC = 5Q + 5Q = 10Q

MC = ΔTC/ΔQ = 10

Set MR = MC to maximize profit

90 – Q = 10

Q = 80

Substituting Q = 80 into the demand function

P = 90 – ½(80) = 50

Profit = TR – TC = P * Q – 10Q = 50 * 80 – 10 * 80 = 3,200

 

14. Assume the rice market was changed from perfect competition to monopoly. Which of the following predictions regarding the rice market is true?

(A) The price of rice decreases.

(B) Consumer surplus decreases.

(C) Producer surplus decreases.

(D) A net social gain occurs.

(E) The consumption of rice increases.

 

Correct Answer: B

 

15. Consider the only coal mining firm in the market. The total cost function is: TC = 100 – 5Q + Q², and the market demand is P = 55 – 2Q. What is the deadweight loss from monopoly power?

Suppose the government sets a maximum price at $27 per unit.

Find the following:

1) market price and quantity

2) the firm’s profit

3) consumer surplus, and

4) deadweight loss both before and after the price ceiling is imposed.

 

Answer:

Before the price ceiling is imposed:

P = 55 – 2Q, TR = P*Q = 55Q – 2Q²

MR = dTR/dQ = 55 – 4Q

MC = dTC/dQ = 2Q-5

Set MR = MC

55 – 4Q = 2Q-5

Q = 10, P = 55 – 2(10) = $35

Economic profit = TR – TC = 35 * 10 – (100 – 5 * 10 + 10²) = 200

Substituting Q = 0 into P = 55 – 2Q

The choke price = 55

CS = (0.5) * 10 * (55 – 35) = $100

The deadweight loss is shown in the area below the demand curve, above the marginal cost curve, and between the quantities of 10 and 15.

DWL = 0.5 * (35 – 15) (15 – 10) = $50

After the imposition of the price ceiling:

P_max = $27 < 35, so this price ceiling is effective.

Substituting P = $27 into the demand equation P = 55 – 2Q

27 = 55 – 2Q

Q = 14. P = 27

Economic profits = TR – TC = 27 * 14 – (100 – 5 * 14 + 14²) = 152

CS = (0.5) * (55 – 27) * (14) = 196

DWL = 0.5 * (15 – 14) (27 – 23) = 2

 

16. Suppose a monopolist has a market demand of P = 120 – 3Q and the firm’s marginal cost curve is constant, MC = 50. The government has imposed a $1 tax on each unit of goods sold. How much has the price changed?

(A) $1

(B) $0.51

(C) $2.30

(D) $1.10

(E) Not enough information

 

Correct Answer: B

Steps:

Initially:

P = 120 – 3Q

MR = 120 – 6Q

MC = 50 before tax

Set MC = MR to maximize profit

120 – 6Q = 50

Q_m = 11.67

P_m = 120 – 3 * 11.67 = $84.99

After the tax is imposed

MC_t = MC + t = 50 + 1 = 51

Set 120 – 6Q = 51

Q = 11.5

Substituting Q = 11.5 into P = 120 – 3Q

P = 120 – 3 * 11.5 = $85.5

$85.5 – $84.99 = $0.51

After the tax is imposed, the price increases by $0.51

 

17. Consider a monopolist with the following total cost function: TC(q) = 55 + q². Assume the market demand is given as: P = 60 – 2q. The profit-maximizing price and quantity are______, and the economic profit is ______.

(A) P = 10, Q = 40; 225

(B) P = 20, Q = 10; 345

(C) P = 40, Q = 10; 245

(D) P = 10, Q = 20; 245

 

Answer: C

Steps:

P = 60 – 2q

MR = 60 – 4q

TC(q) = 55 + q²

MC = ΔTC/ΔQ = 2q

Set MR = MC to maximize profit

60 – 4q = 2q

q = 10

Substituting q = 10 into P = 60 – 2q

P = 40

Economic profit = TR – TC = P * q – TC = 40 * 10 – (55 + 10²) = 245