Topic 7 Practice Questions

1. Consider the market for paper. The market supply and demand functions are given as:

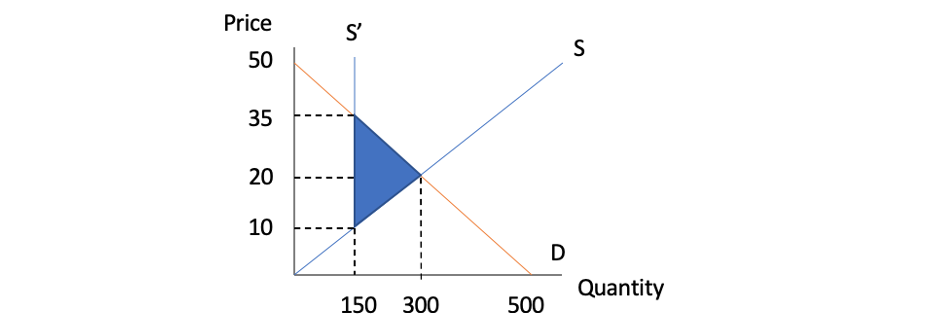
Assume the government imposes a production quota of 150 units of paper. What is the deadweight loss as a result of this production quota?

(A) 1,875

(B) 3,000

(C) 1,125

(D) 750

 

Correct Answer: A

Steps:

Set Q_s = Q_d

15P = -10P + 500

P = 20, Q = 300

The free-market equilibrium price is $20 and the market quantity is 300.

With the quota, Q_d = -10P + 500 = 150

Solve for P, P = 35

The market price is $35 with the production quota.

Substituting Q = 150 into Q_s = 15P. P = 10

The deadweight loss = 0.5*(35-10)(300-150) = 1,875

 

 

2. The market demand and supply function for Good A are given by:

The federal government plans to levy a flat tax on each unit of Good A produced. How much tax should the federal government levy if they want to stabilize the price that sellers receive at $10?

(A) $2

(B) $4

(C) $6

(D) $10

 

Correct Answer: B

Steps:

P_b – P_s = t

Set P_s = $10, P_b = 10 + t

Equate Q_d and Q_s

200 – 5P_b = 100 + 3P_s

200 – 5(10 + t) = 100 + 3*10

200 – 50 – 5t = 100 + 30

20 = 5t

Solve for t

t = 4

 

3. Which of the following statements are true and which are false?

i) The government buys the excess supply to maintain price support.

ii) If demand is more elastic relative to supply, the tax burden falls mostly on buyers.

iii) Deadweight loss is the net loss of total surplus.

iv) A price ceiling is the maximum amount a seller is allowed to charge for a product or service.

 

Correct Answer:

(i) True

(ii) False

(iii) True

(iv) True

 

4. The market for iPhone cases is given by the following:

Q_S = 2P – 35

Q_D = 100 – 2.5P

Calculate the consumer surplus and total surplus at the market-clearing price.

(A) Total surplus is 281.25 while consumer surplus is 125.

(B) Total surplus is 125 while consumer surplus is 281.25.

(C) Total surplus is 281.25 while consumer surplus is 156.25.

(D) Total surplus is 156.25 while consumer surplus is 125.

(E) More information is needed to calculate the total and consumer surplus.

 

Correct Answer: A

Steps:

Find the market-clearing price and quantity.

2P – 35 = 100 – 2.5P

P = $30

Substitute P = $30 into the supply equation Q_S = 2P – 35.

Q = 2P – 35

Q = 2(30) – 35

Q = 25

Next, find the vertical intercept of the demand curve and supply curve.

Set Q = 0

Q_D = 100 – 2.5P

0 = 100 – 2.5P

P = 40 (vertical intercept of the demand curve)

Q_S = 2P – 35

0 = 2P – 35

P = 17.5 (vertical intercept of the supply curve)

Find the total surplus.

TS = 0.5*(40 – 17.5) * 25

TS = 281.25

Find the consumer surplus.

CS = 0.5*(40 – 30) *25

CS = 125

 

5. Suppose the clothing market is competitive, and is characterized by the following demand and supply functions:

Q_d = 520 – 40P

Q_s = -80 + 160P

The government imposes a unit tax of $2.50 on clothing. Find the deadweight loss caused by the tax.

(A) 100

(B) 200

(C) 300

(D) 400

(E) 500

 

Correct Answer: A

Steps:

Equate Q_d = Q_s

P_b – P_s = 2.50

520 – 40P_b = -80 + 160P_s

Replace P_b using P_s + 2.50:

520 – 40(P_s + 2.50) = -80 + 160P_s

520 – 40P_s – 100 = -80 + 160P_s

Solve for P_s

P_s = 2.5

P_b = P_s + 2.50 = 5

Substituting P_s = 2.5 into Q_s = -80 + 160Ps

Q_s = -80 + 160(2.5) = 320

Find the free-market equilibrium price and quantity.

Set Q_d = Q_s

520 – 40P = -80 + 160P

P = 3, Q = 400

Deadweight loss = (1/2) x (2.50) x (400 – 320) = 100

 

6. Suppose that the demand and supply curve of wheat is given as:

Q_D = 750 – 145P

Q_S = 184 + 138P

where Q is measured in millions of bushels and P is the price per bushel. Due to COVID-19, the government maintains the price of wheat at $3.50 per bushel by purchasing any excess supply. Find the cost to the government and the change in consumer surplus caused by this price support program.

(A) $1456.62; -$526.61

(B) $1449.51; -$486.29

(C) $1485.75; -$486.29

(D) $1485.75; -$526.61

 

Correct Answer: D

Steps:

At P = $3.5, excess supply = Q_S – Q_D = 184 + 138P – (750 – 145P) = 424.5

The government’s cost = $3.5 * 424.5 = $1485.75

Next, find the change in consumer surplus.

Set Q_D = Q_S

750 – 145P = 184 + 138P

P = $2, Q = 460

The free-market equilibrium price and quantity: P = $2, Q = 460

Now, find the vertical intercept of the demand curve.

Q_D = 750 – 145P

Set Q_D = 0 and solve for P.

P = 750 / 145 = 5.17

The vertical intercept of the demand curve is $5.17.

Find the consumer surplus at free-market equilibrium price.

CS = 0.5 * (5.17 – 2) * 460 ≈ 729.1

Find the consumer surplus with price support.

Substituting P = 3.5 into Q_D = 750 – 145P, Q_D = 750 – 145 * 3.5 = 242.5

CS = 0.5 * (5.17 – 3.5) * 242.5 ≈ 202.49

The change in consumer surplus = 202.49 – 729.1 ≈ -526.61

 

7. Which of the following statements are true and which are false?

I: Externalities are the only reason for market failure.

II: The impact of a negative externality is accounted for by the market price.

 

Correct Answer: 

(I) False. Asymmetric information and public good are also reasons for market failure.

(II) False. The impact of a negative externality is not transmitted via price.

 

8. Assume the following equations model the supply and demand curves for Netflix:

Q_d = 35 – 3P

Q_s = 15 + 2P

The Canadian government has decided to implement a per-unit tax of $4 on the service. How much more does the buyer pay after the tax is imposed compared to what they were paying before?

(A) $1.60

(B) $5.60

(C) $4

(D) $4.80

(E) The seller would assume the burden of the tax and the buyer would not notice a price change.

 

Correct Answer: A

Steps:

First, find the market equilibrium price before the tax is imposed.

Set Q_d = Q_s, and solve for P. P = $4, and Q = 23.

With the unit tax, P_b = Ps + 4

Set Q_d = Q_s

35 – 3P_b = 15 + 2P_s

Substitute P_b = P_s + 4 into the above equation.

35 – 3(P_s + 4) = 15 + 2P_s

5P_s = 8

P_s = 8/5 = 1.6 ⇒ P_b = 1.6 + 4 = 5.6

Then, the change in consumer price = 5.6 – 4 = 1.6

Buyers now pay $1.60 more than they used to.

 

9. The market demand and supply functions for fabric are:

Q_d = 20 – 0.25P

Q_s = P – 20

Assume the government sets a price floor at $40. What is the change in consumer surplus after this price floor is implemented?

(A) -$100

(B) -$88

(C) -$66

(D) 0

 

Correct Answer: B

Steps:

First, find the free-market equilibrium price and quantity.

Set Q_d = Q_s

20 – 0.25P = P – 20

40 = 1.25P

P = 32, Q= 12

Find the vertical intercept of the demand curve.

Set Q_d = 0, 20 – 0.25P = 0

P = 80

CS = 0.5 * (80 – 32) * 12 = 288

After the price floor is implemented, Q_d = 20 – 0.25(40) = 10

CS = 0.5 * (80 – 40) * 10 = 0.5(10 * 40) = 200

ΔCS = 200 – 288 = -88

After the price floor is implemented, the consumer surplus decreases by $88.

 

10. The market for corn is perfectly competitive with the market demand and supply functions given as:

Q_d = 200 – 20P

Q_s = 80 + 10P

Where Q_d and Q_s are measured in millions of bushels, and P is measured in dollars per bushel. Suppose the government implements a unit tax of $2.50 on corn. Answer the following:

(A) Find the free-market equilibrium price and quantity.

(B) Find the equilibrium price and quantity after the imposition of the unit tax.

(C) Calculate the government tax revenue.

(D) What is the deadweight loss caused by the unit-tax?

 

Answer:

(A) Find the free-market equilibrium price and quantity.

Set Q_d = Q_s

200 – 20P = 80 + 10P

P₀ = 4, Q₀ = 120

At the free-market equilibrium, the price of wheat is $4 per bushel, and the quantity is 120 million bushels.

(B) Find the market price and quantity after the imposition of the tax.

Set Q_d = Q_s

Substituting P_b = P_s + 2.5 into the demand function.

200 – 20(P_s + 2.5) = 80 + 10P_s

P_s = 2.33

P_b = P_s + 2.5 = 4.83

Q = 103.33

After the imposition of the tax, consumers pay $4.83 per bushel, and sellers receive $2.33 per bushel. The after-tax equilibrium quantity is 103.33 million bushels.

(C) Calculate the government tax revenue.

Tax revenue = $2.50 × 103.33 = $258.33 million

(D) Calculate the deadweight loss for corn caused by the unit tax.

DWL = 0.5 × 2.50 × (120 – 103.33) = $20.84 million

 

11. In a competitive market, the market-clearing price is $5.30 and the quantity is 20. At P = $5.30, the consumer surplus of this market is 47. Assume the market demand function is linear. Derive the market demand function based on the above information.

 

Answer:

P = 10 – 0.235Q

Steps:

Assume the demand function is P = a – bQ

CS = 0.5 * (a – 5.3) * 20 = 47

Solve for a.

a = 10

Substituting P = 5.3, Q = 20, a = 10 into the demand function P = a – bQ.

5.3 = 10 – b * 20

b = 0.235

The market demand function is: P = 10 – 0.235Q

 

12. Market failure occurs in a situation where a/an ________ competitive market is ___________ because prices _______ provide proper signals to consumers and producers.

(A) regulated, efficient, fail to

(B) unregulated, efficient, successfully

(C) regulated, inefficient, successfully

(D) unregulated, inefficient, fail to

 

Correct Answer: D

 

13. Which of the following is an example of a negative externality?

(A) A third-party firm decides to ruin another firm’s reputation by spreading false rumours about them.

(B) An individual using winter tires creates a safer driving environment for all the other drivers around him or her.

(C) An increase in air travel leads to air pollution, which poses a negative impact on other members of the society.

(D) A beekeeper’s bees extract nectar from a neighbour’s apple tree orchard.

 

Correct Answer: C

 

14. In what circumstance does the burden of the tax fall mostly on sellers?

(A) When demand and supply are equally elastic.

(B) When supply is more elastic relative to demand.

(C) When demand and supply are equally inelastic.

(D) When demand is more elastic relative to supply.

 

Correct Answer: D

 

15. Assume the market demand and supply curves of gasoline are:

Q_d = 180 – 30P_b

Q_s = 70 + 25P_s

Assume a $2 per litre gasoline tax is imposed. The after-tax market quantity is:

(A) 87.3

(B) 92.7

(C) 82.7

(D) 103.3

 

Correct Answer: B

Steps:

Set Q_d = Q_s

180 – 30P_b = 70 + 25P_s

Substituting P_b = P_s + 2 into the above equation

180 – 30(P_s + 2) = 70 + 25P_s

25P_s + 30P_s = 180 – 70 – 60

55P_s = 50

P_s = 0.91

P_b = 0.91 + 2 = 2.91

Q = 180 – (30)(2.91) = 180 – 87.3 = 92.7