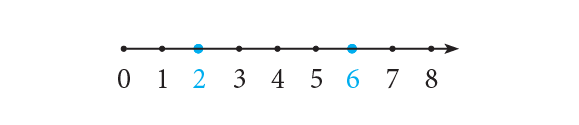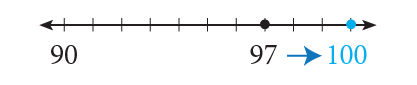1.1 Understanding Whole Numbers
Place Value of Whole Numbers

All numbers can be made up using the digits 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9. Numbers may consist of one or more digits. When a number is written using the above digits, it is said to be in standard form.
For example, 7, 85, and 2,349 are examples of numbers in their standard form, where 7 is a single- (one) digit number, 85 is a two-digit number, and 2,349 is a four-digit number.
The position of each digit in a whole number determines the place value for the digit.
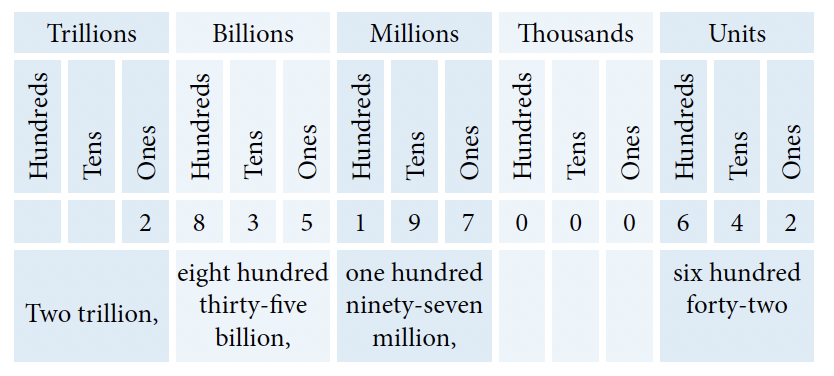
Exhibit 1.1-a illustrates the place value of each of the ten digits in the whole number: 3,867,254,129. In this whole number, 4 occupies the 'thousands' place value and represents 4 thousand (or 4,000), whereas 7 occupies the 'millions' place value and represents 7 million (or 7,000,000).
The place value of 'ones' is [latex]10^0[/latex] ( = 1), and each position has a value of 10 times the place value to its right, as shown in Table 1.1.
| Exponent Form | Standard Form | Place Value |
|---|---|---|
| [latex]10^9[/latex] | 1,000,000,000 | Billions |
| [latex]10^8[/latex] | 100,000,000 | Hundred millions |
| [latex]10^7[/latex] | 10,000,000 | Ten millions |
| [latex]10^6[/latex] | 1,000,000 | Millions |
| [latex]10^5[/latex] | 100,000 | Hundred thousands |
| [latex]10^4[/latex] | 10,000 | Ten thousands |
| [latex]10^3[/latex] | 1,000 | Thousands |
| [latex]10^2[/latex] | 100 | Hundreds |
| [latex]10^1[/latex] | 10 | Tens |
| [latex]10^0[/latex] | 1 | Ones |
We read and write numbers from left to right. A number in standard form is separated into groups of three digits using commas. The vertical red lines in Table 1.1 denote the positions of the commas that separate the groups of three digits, starting from the place value for 'ones'. For example, the ten-digit number in Exhibit 1.1a is written as 3,867,254,129 in its standard form.
| Digit | 3 | 8 | 6 | 7 | 2 | 5 | 5 | 1 | 2 | 9 |
|---|---|---|---|---|---|---|---|---|---|---|
| Place Value | Billions | Hundred millions |
Ten millions |
Millions | Hundred thousands |
Ten thousands |
Thousands | Hundreds | Tens | Ones |
Numbers can also be written in expanded form by writing the number as the sum of what each place value represents.
For example, the number 3,867,254,129 in standard form can be written in expanded form as follows:
3,000,000,000 + 800,000,000 + 60,000,000 + 7,000,000 + 200,000 + 50,000 + 4,000 + 100 + 20 + 9
Or,
3 billion + 800 million + 60 million + 7 million + 200 thousand + 50 thousand + 4 thousand + 1 hundred + 2 tens + 9 ones
Example 1.1a: Identifying the Place Value of a Digit and the Amount it Represents
What is the place value of the digit 5 in each of the following numbers and what amount does it represent?
- $2,543
- $75,342
- $6,521,890
- $915,203,847
| Dollar Amount | Place Value | Amount Represented |
|---|---|---|
| 1. $2,543 | Hundreds | $500 |
| 2. $75,342 | Thousands | $5,000 |
| 3. $6,521,890 | Hundred thousands | $500,000 |
| 4. $915,203,847 | Millions | $5,000,000 |
Example 1.1b: Identifying the Digit of a Number Given its Place Value
In the number 5,320,948, identify the digit that occupies the following place values:
- Hundred thousands
- Ten thousands
- Thousands
- Tens
- Hundreds
- Millions
| Place Value | Digit Located in Place Value |
|---|---|
| 1. Hundred thousands | 3 |
| 2. Ten thousands | 2 |
| 3. Thousands | 0 |
| 4. Tens | 4 |
| 5. Hundreds | 9 |
| 6. Millions | 5 |
Example 1.1c: Identifying the Digit of a Number Given its Place Value
Write the following numbers in expanded form:
- 698
- 8,564
- 49,005
- 521,076
- 9,865,323
- 43,583,621
| Number | Expanded Form |
|---|---|
| 1. 698 | 600 + 90 + 8 |
| 2. 8,564 | 8,000 + 500 + 60 + 4 |
| 3. 49,005 | 40,000 + 9,000 + 5 |
| 4. 521,076 | 500,000 + 20,000 + 1,000 + 70 + 6 |
| 5. 9,865,323 | 9,000,000 + 800,000 + 60,000 + 5,000 + 300 + 20 + 3 |
| 6. 43,583,621 | 40,000,000 + 3,000,000 + 500,000 + 80,000 + 3,000 + 600 + 20 + 1 |
Reading and Writing Whole Numbers
To make it easier to read and write numbers, any number larger than three digits is separated into smaller groups of three digits, starting from the last digit of the number. Each of these groups of three digits has a name.
- The first group of three digits on the right is the “Units” group.
- The second group from the right is the “Thousands” group.
- The third group from the right is the “Millions” group.
- The fourth group from the right is the “Billions” group.
- The fifth group from the right is the “Trillions” group and so on, as shown in the following chart.
 Follow these steps to write large numbers in word form:
Follow these steps to write large numbers in word form:
- Start from the group furthest to the left and write the number formed by the digits in that group, followed by the group's name.
- Moving to the next group (to the right), write the numbers formed by this next group, followed by its name. Continue to do this for each of the groups.
- For the last group (i.e., the group furthest to the right), write the numbers formed by the group; however, for this group, do not write the name of it.
Note: When a group contains all zeros, that group is neither read nor written.
For example, 2,835,197,000,642 expressed in word form using the above rules would be as follows:
When writing numbers in word form, the names of the groups remain in their singular forms, irrespective of the number preceding, i.e., hundred, thousand, million, billion, trillion, etc.

Example 1.1d: Writing Numbers in Word Form Given their Standard Form
Write the following numbers in word form:
- 743
- 5,006
- 15,017
- 800,629
- 6,783,251
- 52,630,042
| Number | Word Form |
|---|---|
| 1. 743 | Seven hundred forty-three |
| 2. 5,006 | Five thousand, six |
| 3. 15,017 | Fifteen thousand, seventeen |
| 4. 800,629 | Eight hundred thousand, six hundred twenty-nine |
| 5. 6,783,251 | Six million, seven hundred eighty-three thousand, two hundred fifty-one |
| 6. 52,630,042 | Fifty-two million, six hundred thirty thousand, forty-two |
Example 1.1e: Writing Numbers In Standard Form Given their Word Form
Write the following numbers in standard form:
- Two hundred five
- Six thousand, four
- Thirty-five thousand, eight hundred twenty-five
- Eight hundred thousand, five
- Two million, three hundred forty-two thousand, six hundred seventeen
- Half of a million
- One-quarter of a billion
| Number in Word Form | Number in Standard Form |
|---|---|
| 1. Two hundred five | 205 |
| 2. Six thousand, four | 6,004 |
| 3. Thirty-five thousand, eight hundred twenty-five | 35,825 |
| 4. Eight hundred thousand, five | 800,005 |
| 5. Two million, three hundred forty-two thousand, six hundred seventeen | 2,342,617 |
| 6. Half of a million |
[latex]1,000,000 \div 2= 500,000[/latex] |
| 7. One-quarter of a billion | [latex]1,000,000,000 \div 4= 250,000,000[/latex] |
Representing Whole Numbers on a Number Line
As shown below, whole numbers can be represented graphically as a point on a horizontal line, called the number line.
The arrowhead at the end shows that the line continues indefinitely in that direction.
The smallest whole number is zero (0). It is not possible to find the largest whole number because, for any given number, there will always be another number greater than that number.
Writing numbers on a number line helps in comparing and identifying numbers that are smaller or larger than other numbers. Numbers that lie to the left of a number on the number line are less than (i.e., smaller than) that number, and those that lie to the right on the number line are greater than (i.e., larger than) that number.
For example,
- 6 is greater than 2 (or 2 is less than 6).
- 5 is less than 7 (or 7 is greater than 5).
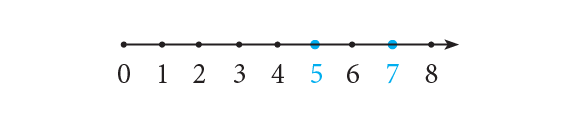
The signs used to show the relative position of two numbers (or quantities) are:
- ‘ > ’ read as “greater than”, meaning that the number on the left of the sign has a value greater than that on the right.
For example, “6 is greater than 2” is written as 6 > 2.
This is the same as “2 is less than 6, " written as 2 < 6.
- ‘ < ’ read as “less than”, meaning that the number on the left of the sign has a value less than that on the right.
For example, “5 is less than 7” is written as 5 < 7.
This is the same as “7 is greater than 5”, written as 7 > 5.
Example 1.1f: Plotting Numbers on a Number Line and Using Signs to Show the Relative Positions of the Numbers
Plot the following numbers on a number line and place the correct sign of inequality, ‘>’ or ‘<’, in the space (indicated by underscore) between the numbers.
- 7 _ 11
- 7 _ 5
- 11 _ 5
- 5 _ 12
- 3 _ 5
- 12 _ 11
Solution
- 7 < 11
- 7 > 5
- 11 > 5
- 5 < 12
- 3 > 5
- 12 > 11
Example 1.1g: Writing a Statement to Represent ‘>’ or ‘<’
Write statements using the words “greater than” or “less than” for the following expressions:
- 24 > 22
- 36 < 39
- 9 > 0
- 0 < 5
Solution for Example 1.1g
- 24 is greater than 22, or 22 is less than 24.
- 36 is less than 39, or 39 is greater than 36.
- 9 is greater than 0, or 0 is less than 9.
- 0 is less than 5, or 5 is greater than 0.
Rounding Whole Numbers
Rounding numbers makes them easier to work with and easier to remember. Rounding changes some of the digits in a number but keeps its value close to the original. It is used in reporting large quantities or values that change often, such as population, income, expenses, etc.
For example, the population of Canada is approximately 37 million, or Henry’s car expense for this month is approximately $700.
Rounding numbers also makes arithmetic operations faster and easier, especially when determining the exact answer is not required.
For example, if you are required to estimate the area of a rectangular plot of land that measures 114 m by 97 m, you would have to multiply 114 × 97, resulting in 11,058 [latex]m^2[/latex]. However, rounding the measurements to the nearest ten can provide a quick estimate.
Rounding Whole Numbers to the Nearest Ten, Hundred, Thousand, etc.
Rounding whole numbers refers to changing the value of the whole number to the nearest ten, hundred, thousand, etc. It is also called rounding whole numbers to a multiple of 10, 100, 1,000, etc.
- Rounding a whole number to the nearest ten is the same as rounding it to a multiple of 10.
- Rounding a whole number to the nearest hundred is the same as rounding it to a multiple of 100.
- Rounding an amount to the nearest $1,000 is the same as rounding the amount to a multiple of $1,000.
For example, rounding the measurements of the above-mentioned plot of land to the nearest ten (or multiple of 10):
- Rounding 114 to the nearest ten results in 110. 114 is closer to 110 than 120. Therefore, round down to 110.
Therefore, rounding the measurements to the nearest ten results in an estimated area of 110 m × 100 m = 11,000 [latex]m^2[/latex].
Follow these steps to round whole numbers:
- Identify the digit to be rounded (this is the place value for which the rounding is required).
- If the digit to the immediate right of the required rounding digit is less than 5 (0, 1, 2, 3, 4), do not change the value of the rounding digit.
If the digit to the immediate right of the required rounding digit is 5 or greater than 5 (5, 6, 7, 8, 9), increase the value of the rounding digit by one (i.e., round up by one number). - Change the value of all digits to the right of the rounding digit to 0.
Example 1.1-h: Rounding Numbers Using a Number Line (Visual Method)
Round the following numbers to the indicated place value using a number line:
- 624 to the nearest ten (multiple of 10).
- 150 to the nearest hundred (multiple of 100).
- 1,962 to the nearest hundred (multiple of 100).
Solution
- 624 to the nearest ten (multiple of 10). 624 is closer to 620 than it is to 630. Therefore, 624 rounded to the nearest ten is 620.
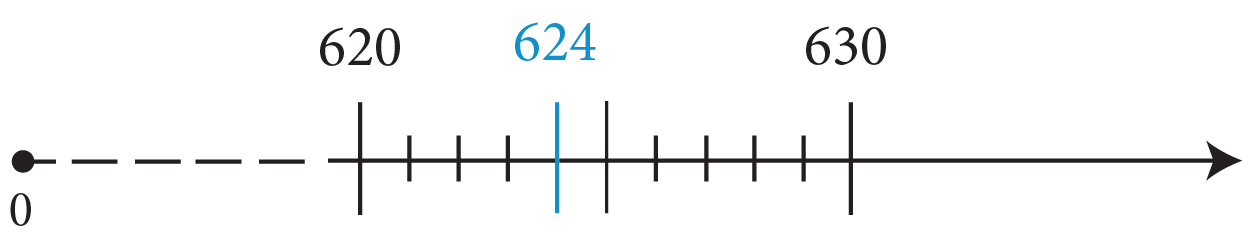
- 150 to the nearest hundred (multiple of 100). 150 is exactly midway between 100 and 200. By convention, if a number is exactly in the middle, we round up. Therefore, 150 rounded to the nearest hundred is 200.
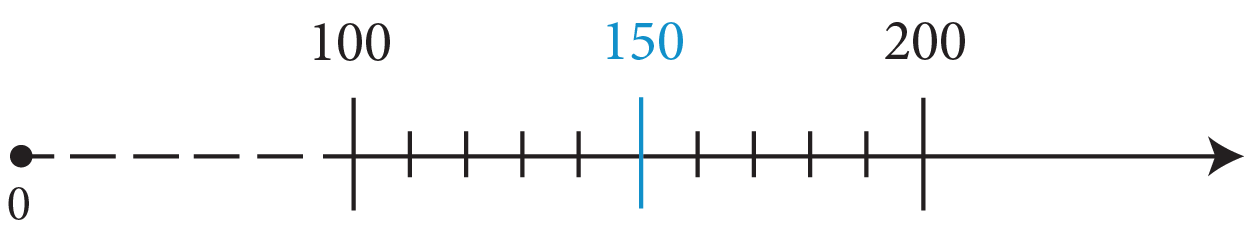
- 1,962 to the nearest hundred (multiple of 100). 1,962 is closer to 2,000 than it is to 1,900. Therefore, 1,962 rounded to the nearest hundred is 2,000.
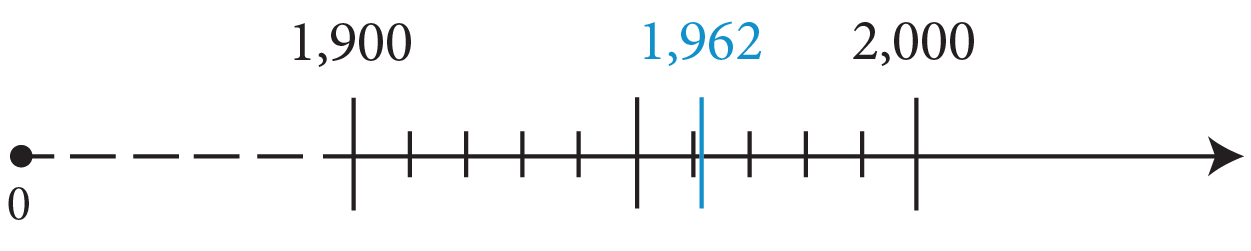
Follow these steps to round whole numbers:
- Identify the digit to be rounded (this is the place value for which the rounding is required).
- If the digit to the immediate right of the required rounding digit is less than 5 (0, 1, 2, 3, 4), do not change the value of the rounding digit.
If the digit to the immediate right of the required rounding digit is 5 or greater than 5 (5, 6, 7, 8, 9), increase the value of the rounding digit by one (i.e., round up by one number). - Change the value of all digits to the right of the rounding digit to 0.
Example 1.1-i: Rounding to Indicated Place Values
Round the following numbers to the indicated place value using a number line:
- $568 to the nearest $10.
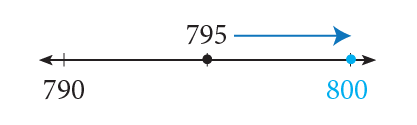
- $795 to the nearest $10.
- $5,643 to the nearest $100.
- $19,958 to the nearest $100.
Solution
- Rounding $568 to the nearest $10:
Identify the rounding digit in the tens place: 568 (6 is the digit in the tens place).
The digit to the immediate right of the rounding digit is 8, which is greater than 5; therefore, increase the value of the rounding digit by one, from 6 to 7, and change the value of the digits that are to the right of the rounding digit to 0, which will result in 570.
Therefore, $568 rounded to the nearest $10 (or multiple of $10) is $570.
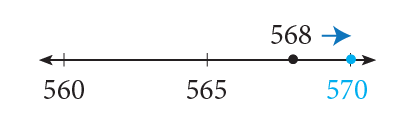
- Rounding $568 to the nearest $10:
Identify the rounding digit in the tens place: 568 (6 is the digit in the tens place).
The digit to the immediate right of the rounding digit is 8, which is greater than 5; therefore, increase the value of the rounding digit by one, from 6 to 7, and change the value of the digits that are to the right of the rounding digit to 0, which will result in 570.
Therefore, $568 rounded to the nearest $10 (or multiple of $10) is $570.
- Rounding $568 to the nearest $10:
Identify the rounding digit in the tens place: 568 (6 is the digit in the tens place).
The digit to the immediate right of the rounding digit is 8, which is greater than 5; therefore, increase the value of the rounding digit by one, from 6 to 7, and change the value of the digits that are to the right of the rounding digit to 0, which will result in 570.
Therefore, $568 rounded to the nearest $10 (or multiple of $10) is $570.

- Rounding $568 to the nearest $10:
Identify the rounding digit in the tens place: 568 (6 is the digit in the tens place).
The digit to the immediate right of the rounding digit is 8, which is greater than 5; therefore, increase the value of the rounding digit by one, from 6 to 7, and change the value of the digits that are to the right of the rounding digit to 0, which will result in 570.
Therefore, $568 rounded to the nearest $10 (or multiple of $10) is $570.

1.1 Exercises
Answers to the odd-numbered questions are available at the end of the book.
- a. 4,792
b. 5,352
c. 45,721 - a. 7,628
b. 4,687
c. 94,083 - a. 319,526
b. 7,825,500
c. 16,702,555 - a. 204,095
b. 35,217,123
c. 4,385,207
For Problems 5 to 10, (i) write the numbers in their expanded form and (ii) word form.
- a. 407
b. 2,056 - a. 860
b. 7,805 - a. 29,186
b. 464,448 - a. 94,975
b. 684,137 - a. 2,604,325
b. 15,300,604 - a. 9,084,351
b. 23,006,045
For Problems 11 to 16, (i) write the numbers in their standard form and (ii) word form.
- a. 600 + 70 + 9
b. 3,000 + 100 + 40 + 7 - a. 400 + 50 + 6
b. 1,000 + 900 + 30 + 2 - a. 2,000 + 600 + 5
b. 9,000 + 20 + 4 - a. 5,000 + 300 + 1
b. 7,000 + 80 + 8 - a. 40,000 + 900 + 90
b. 10,000 + 50 + 3 - a. 60,000 + 700 + 80
b. 20,000 + 100 + 4
For Problems 17 to 24, (i) write the numbers in their standard form and (ii) in expanded form.
- a. Five hundred seventy
b. Eight hundred three - a. One thousand, five
b. Seven thousand, twenty - a. Eighty thousand, six hundred thirty
b. Seventy-five thousand, twenty-five - a. Sixty-five thousand, two hundred forty-four
b. Eight hundred thirty-three thousand, six hundred forty-one - a. Twelve million, four hundred fifty-two thousand, eight hundred thirty-two
b. Thirty-two million, six hundred eighty-four thousand, two hundred fifty-six - a. Two billion, one thousand
b. One billion, twenty-five thousand - a. One-eighth of a million
b. One-quarter of a million - a. Half of a billion
b. One-tenth of a billion
For Problems 25 and 26, plot the numbers on a number line.
- a. 14, 19, 15, 7
b. 12, 8, 17, 5 - a. 18, 9, 6, 11
b. 4, 10, 7, 16
For Problems 27 and 28, place the correct sign ‘>’ or ‘<’ in the space between the numbers (indicated by underscore).
- a. 7 _ 15
b. 19 _ 14
c. 0 _ 5
d. 19 _ 0 - a. 12 _ 17
b. 8 _ 5
c. 17 _ 0
d. 0 _ 8
For Problems 29 and 30, express the relationship between the numbers using the statements (i) “less than” and (ii) “greater than”.
- a. 6 < 9
b. 18 > 11
c. 5 < 11
d. 11 > 0 - a. 4 < 7
b. 16 > 7
c. 10 < 16
d. 0 < 4
For Problems 31 to 34, arrange the numbers in order from least to greatest.
- a. 87; 108; 99; 103; 96
b. 159; 141; 108; 139; 167 - a. 58; 129; 147; 49; 68
b. 836; 820; 805; 873; 875 - a. 2,067; 2,040; 2,638; 2,533
b. 79,487; 79,534; 79,468; 78,812 - a. 2,668; 2,630; 2,579; 2,759
b. 68,336; 69,999; 69,067; 68,942
For Problems 35 and 36, create the least and greatest possible numbers using all the given digits.
- a. 9, 2, 5
b. 7, 9, 1, 8
c. 3, 5, 4, 8 - a. 6, 1, 7
b. 9, 4, 8, 5
c. 4, 7, 2, 6, 5
For Problems 37 and 38, round the numbers to the nearest ten, nearest hundred, and nearest thousand.
-
Number Nearest Ten Nearest Hundred Nearest Thousand a. 524 b. 1,645 c. 53,562 d. 235,358
-
Number Nearest Ten Nearest Hundred Nearest Thousand a. 895 b. 9,157 c. 25,972 d. 139,835
For Problems 39 and 40, round the numbers to nearest ten thousand, nearest hundred thousand, and nearest million.
-
Number Nearest Ten Thousand Nearest Hundred Thousand Nearest Million a. 875,555 b. 1,656,565 c. 3,368,850 d. 4,568,310
-
Number Nearest Ten Thousand Nearest Hundred Thousand Nearest Million a. 759,850 b. 3,254,599 c. 7,555,450 d. 2,959,680
Unless otherwise indicated, this chapter is an adaptation of the eTextbook Foundations of Mathematics (3rd ed.) by Thambyrajah Kugathasan, published by Vretta-Lyryx Inc., with permission. Adaptations include supplementing existing material and reordering chapters.