8.4 Parallel and Perpendicular Lines
Parallel Lines
Lines that never intersect are called parallel lines. All lines with the same slope are parallel to each other.
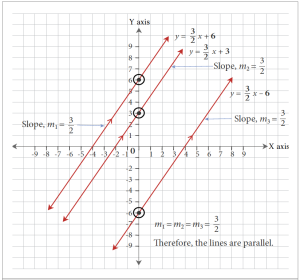
Lines represented by the equations [latex]\displaystyle{y = \frac{3}{2}x + 6}[/latex], [latex]\displaystyle{y = \frac{3}{2}x + 3}[/latex], and [latex]\displaystyle{y = \frac{3}{2}x - 6}[/latex] have the same slope (equal to [latex]\displaystyle{\frac{3}{2}}[/latex]). Therefore, they are all parallel to each other.
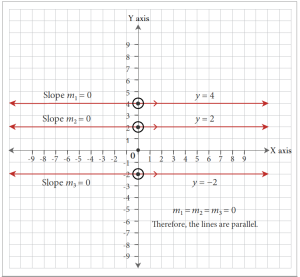
All horizontal lines are parallel to each other and all vertical lines are parallel to each other. For example, lines represented by the equations [latex]y = 4[/latex], [latex]y = 2[/latex], and [latex]y = -2[/latex] are horizontal lines and have slopes equalling zero. Therefore, they are all parallel to each other. Horizontal lines are also parallel to the X-axis (which has the equation [latex]y = 0[/latex]).
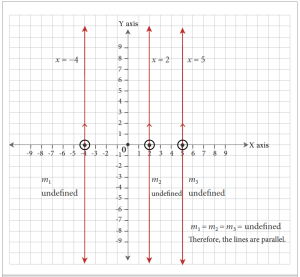
Lines represented by the equations [latex]x =-4[/latex], [latex]x = 2[/latex], and [latex]x = 5[/latex] are vertical lines and have undefined slopes. Therefore, they are all parallel to each other. Vertical lines are also parallel to the Y-axis (which has the equation [latex]x = 0[/latex]).
Example 8.4-a: Writing the Equation of a Line Parallel to a Given Line and Passing Through a Given Point
Write the equation of the line that is parallel to [latex]3x + y = 5[/latex] and passes through the point P(2, 4).
Solution
[latex]3x + y = 5[/latex]
Rearranging to slope-intercept form,
[latex]y = -3x + 5[/latex]
Therefore, the slope is [latex]m = -3[/latex].
The slope of the line parallel to this will have the same slope, [latex]m = -3[/latex].
Let the equation of the line parallel to [latex]3x + y = 5[/latex] be [latex]y= mx + b[/latex].
It passes through (2, 4) and has a slope of [latex]m = -3[/latex].
[latex]y = mx + b[/latex]
Substituting the slope [latex]m = -3[/latex],
[latex]y = -3x + b[/latex]
Substituting the coordinates of the given point (2, 4),
[latex]4 = -3(2) + b[/latex]
Solving for [latex]b[/latex],
[latex]4 = -6 + b[/latex]
[latex]b = 4 + 6 = 10[/latex]
Therefore, the equation of the desired line is [latex]y = -3x + 10[/latex], or [latex]3x + y = 10[/latex] in standard form.
Note: For parallel lines in standard form [latex]Ax + By = C[/latex], the values of [latex]A[/latex] and [latex]B[/latex] will always be proportional, and often will be equal.
Perpendicular Lines
Two lines that meet at a right angle are known as perpendicular lines. If the product of the slopes of two lines is −1, then the two lines are perpendicular. This is the same as stating that if the slope of one line is the negative reciprocal of the other, the two lines are perpendicular.
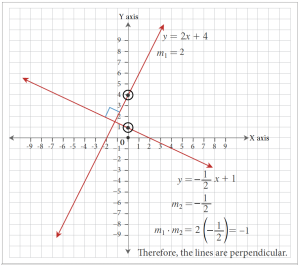
Lines represented by the equations [latex]y = 2x + 4[/latex] and [latex]\displaystyle{y = -\frac{1}{2}x + 1}[/latex] are perpendicular to each other because their slopes are negative reciprocals of each other.[latex]m_1 = 2[/latex], [latex]\displaystyle{m_2 = -\frac{1}{2}}[/latex][latex]\displaystyle{m_1 \cdot m_2 = 2\left(\frac{1}{2}\right) = -1}[/latex].
All vertical lines (slope is undefined) and horizontal lines (slope is zero) are perpendicular.
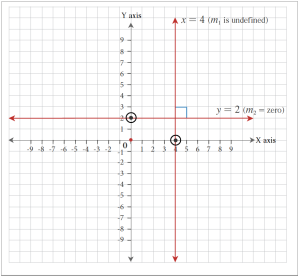
Example 8.4-b: Writing the Equation of a Line Perpendicular to a Given Line and Passing Through a Given Point
Write the equation of the line that is perpendicular to [latex]x + 3y = 9[/latex] and passes through the point P(-4, 2).
Solution
[latex]x + 3y = 9[/latex]
Rearranging to slope-intercept form,
[latex]3y = -x + 9[/latex]
[latex]\displaystyle{3y = -\frac{1}{3}x + 3}[/latex]
Therefore, the slope is [latex]\displaystyle{m = -\frac{1}{3}}[/latex].
The slope of the line perpendicular to this will be the negative reciprocal of [latex]\displaystyle{m = -\frac{1}{3}}[/latex], which is 3.
Let the equation of the line perpendicular to [latex]x + 3y = 9[/latex] be [latex]y = mx + b[/latex]. It passes through the point (−4, 2) and has a slope of [latex]m = 3[/latex].
[latex]y = mx + b[/latex]
Substituting the slope [latex]m = 3[/latex],
[latex]y = 3x + b[/latex]
Substituting the coordinates of the given point (–4, 2),
[latex]2 = 3(-4) + b[/latex]
Solving for [latex]b[/latex],
[latex]2 = -12 + b[/latex]
[latex]2 = -12 + b[/latex]
Therefore, the equation of the desired line is [latex]y = 3x + 14[/latex], or [latex]3x - y = -14[/latex] in standard form.
8.4 Exercises
Answers to the odd-numbered questions are available at the end of the book.
For problems 1 to 7, use the slope property of parallel and perpendicular lines to identify whether each of the pairs of lines is parallel, perpendicular, or neither.
- [latex]y = x + 1[/latex][latex]4x + 4y = -1[/latex]
- [latex]6x - 5y = 10[/latex][latex]\displaystyle{y = -\frac{6}{5}x - 12}[/latex]
- [latex]x - 3y = -60[/latex][latex]\displaystyle{y = \frac{1}{3}x - 4}[/latex]
- [latex]3x - 2y = -12[/latex][latex]2x + 3y = -12[/latex]
- [latex]2x + 5y = -5[/latex][latex]\displaystyle{y = \frac{5}{2}x - 4}[/latex]
- [latex]7x + 4y = 16[/latex][latex]\displaystyle{y = -\frac{4}{7}x + 3}[/latex]
- [latex]3x - 2y = -6[/latex][latex]\displaystyle{y = \frac{3}{2}x - 16}[/latex]
For problems 8 to 15, determine the equations for the lines in slope-intercept form.
- A line parallel to [latex]3y - 2x = 6[/latex] and passing through the point P(2, −3).
- A line parallel to [latex]y = 3x - 1[/latex] and passing through the point P(−2, −4).
- A line parallel to [latex]3x - 9y = -2[/latex] and passing through the y-intercept of the line [latex]5x - y = 20[/latex].
- A line parallel to [latex]3x + y = -2[/latex] and passing through the x-intercept of the line [latex]2x + 3y - 4 = 0[/latex].
- A line perpendicular to [latex]x + y = 3[/latex] and passing through the point P(−2, 5).
- A line perpendicular to [latex]4x + y + 1 = 0[/latex] and passing through the point P(3, 4).
- A line perpendicular to [latex]2x - y = 5[/latex] and passing through the x-intercept of the line [latex]3x + 2y - 6 = 0[/latex].
- A line perpendicular to [latex]3x + y + 9 = 0[/latex] and passing through the y-intercept of the line [latex]2x + 3y - 10 = 0[/latex].
Unless otherwise indicated, this chapter is an adaptation of the eTextbook Foundations of Mathematics (3rd ed.) by Thambyrajah Kugathasan, published by Vretta-Lyryx Inc., with permission. Adaptations include supplementing existing material and reordering chapters.

