7.1 Algebraic Expressions
In arithmetic, we use numbers and operations in expressions. The following are examples of arithmetic expressions:
[latex]25 + 15[/latex], [latex]75 - 22[/latex], [latex]8 \times 9[/latex], [latex]\displaystyle{\frac{9}{5}}[/latex]
In algebra, we use numbers, operations, and variables (letters and symbols that represent various numbers) in expressions. The following are examples of algebraic expressions:
[latex]2x + 5[/latex], [latex]30 - 5y[/latex], [latex]6(2a + 5)[/latex], [latex]\displaystyle{\frac{b + 3}{2}}[/latex]
We can use algebra to translate a statement (using words) into an expression (using numbers, operations, and variables). The following keywords will help in translating written statements into algebraic expressions:
Table 7.1: Arithmetic Operations and their Meanings
| Operation | Key Words |
|---|---|
| Addition (+) | add, sum, total, and, plus, more than, increased by, appreciate, rise |
| Subtraction (−) | subtract, difference, minus, less than, decreased by, depreciate, fall |
| Multiplication (×), (·) | multiply, product, times, of |
| Division (÷) | divide, ratio, divided by, quotient, per |
| Expressed In Words | Expressed as an Algebraic Expression |
|---|---|
| Ten more than a number | [latex]x + 10[/latex] |
| A number more than ten | [latex]10 + x[/latex] |
| Twenty less than a number | [latex]x - 20[/latex] |
| A number less than twenty | [latex]20 - x[/latex] |
| Product of five and a number | [latex]5x[/latex] |
| Divide a number by twenty | [latex]\displaystyle{\frac{x}{20}}[/latex] |
| Divide twenty by a number | [latex]\displaystyle{\frac{20}{x}}[/latex] |
| Half of a number | [latex]\displaystyle{\frac{1}{2}x}[/latex] or [latex]\displaystyle{\frac{x}{2}}[/latex] |
| Twice a number | [latex]2x[/latex] |
| Ten more than the product of two numbers | [latex]xy + 10[/latex] |
| 'x' less than 'y' or 'y' minus 'x' | [latex]y - x[/latex] |
| 'y' less than 'x' or 'x' minus 'y' | [latex]x - y[/latex] |
| Seventy decreased by three times a number | [latex]70 - 3x[/latex] |
| 'm' subtracted from 'n' | [latex]n - m[/latex] |
Table 7.2 Terminology Used in Algebraic Expressions
| Terminology | Description | Examples |
|---|---|---|
| Variable | A number, variable, or a combination of numbers and variables which are multiplied or divided together. | [latex]x, y, a, b[/latex] In the expression [latex]2m + 5n - 6, m[/latex] and [latex]n[/latex] are variables. |
| Term | A letter or symbol used in expressions to represent a varying or unknown quantity. | [latex]\displaystyle{5, x, 5x^2y, 2xy, \frac{4}{a}, \frac{b}{3}}[/latex] are all single terms. The expression [latex]5x + y[/latex] has 2 terms. The expression [latex]\displaystyle{\frac{x}{4} - y^2 + \frac{x}{y} - \frac{1}{x}}[/latex] has 4 terms. |
| Constant | A term that only has a number with no variables. | In the expression [latex]2x + 3y + 5[/latex] the 3rd term, +5, is a constant. In the expression [latex]5x^2 - 8[/latex] the 2nd term, –8, is a constant. |
| Coefficient | The product of all numerical factors in a single term involving a variable. If a coefficient is not present, its value is 1. | In the expression [latex]x3 + 5x2 - 3(2y3)[/latex], the coefficient of the 1st term is 1, the coefficient of the 2nd term is 5, and the coefficient of the 3rd term is –6. |
| Expression | A mathematical phrase made up of a combination of terms and operations. | Expressions with one variable: [latex](2x + 5), (9x - 3)[/latex] Expressions with two variables: [latex](5x - 7y + 5)[/latex], [latex](xy + 3x +7)[/latex] |
| Like terms | Terms that have the same variables and exponents. They differ only in their numerical coefficient. Constant terms are like terms. | [latex]5x[/latex] and [latex]5x[/latex] are like terms. [latex]30a^2[/latex], [latex]-4a^2[/latex], and [latex]9a^2[/latex] are like terms. [latex]5[/latex] and [latex]-9[/latex] are like terms. |
| Unlike terms | Terms that have different variables or the same variables with different exponents. | [latex]12y[/latex] and [latex]3y^2[/latex] are unlike terms. [latex]x[/latex], [latex]y[/latex], and [latex]1[/latex] are unlike terms. [latex]5xy[/latex], [latex]-3x^2y[/latex], and [latex]7xy^2[/latex] are unlike terms. |
| Factors | Refer to each of the combinations of variables and/or numbers multiplied together in a term. | [latex]5[/latex] and [latex]x[/latex] are factors of the term [latex]5x[/latex]. [latex]3[/latex], [latex]x[/latex], and [latex]y[/latex] are factors of the term [latex]3xy[/latex]. |
| Monomial | An algebraic expression that has only one term. | [latex]8[/latex], [latex]7x[/latex], [latex]4y[/latex], and [latex]2xy[/latex] are monomials. |
| Polynomial | An algebraic expression that has two or more terms. | [latex](8x^2 - 5x + 3)[/latex] is a polynomial with 3 terms, where the 1st term is [latex]8x^2[/latex], the 2nd term is [latex]-5x[/latex], and the 3rd term is 3. The coefficient of the 1st term is 8, and the coefficient of the 2nd term is –5. The 3rd term is a constant. |
| Binomial | A polynomial with 2 terms. | [latex](4x - 3y)[/latex], [latex](x - 5)[/latex], [latex](4xy + 7x)[/latex] are binomials. |
| Trinomial | A polynomial with 3 terms. | [latex](2x + 3y + 5)[/latex], [latex](xy + x - 2)[/latex], [latex](2x + xy + 3z)[/latex] are trinomials. |
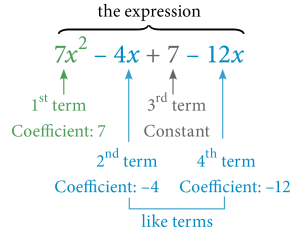
Example 7.1-a: Identifying Components of an Algebraic Expression
Given: [latex]7x^2 - 4x + 7 - 12x[/latex]
Identify the following (if applicable):
- the expression
- the terms
- any like terms
- the coefficients
- the constant
Solution
Evaluating Algebraic Expressions
In an algebraic expression, replacing all the variables with numerical values and simplifying the expression is referred to as evaluating the algebraic expression. The simplified answer is the value of the expression.
Example 7.1-b: Evaluating Algebraic Expressions
Evaluate the following expressions:
- [latex]2x + y[/latex], where [latex]x = 10[/latex] and [latex]y = 5[/latex]
- [latex]\displaystyle{\frac{3xy + 3x}{2y + 5}}[/latex], where [latex]x = 3[/latex] and [latex]y = 2[/latex]
Solution
- [latex]2x + y[/latex] Substituting [latex]x = 10[/latex] and [latex]y = 5[/latex],[latex]= 2(10) + 5[/latex] [[latex]2x[/latex] means [latex]2(x)[/latex]][latex]= 20 + 5 = 25[/latex]
- [latex]\displaystyle{\frac{3xy + 3x}{2y + 5}}[/latex] Substituting [latex]x = 3[/latex] and [latex]y = 2[/latex],[latex]\displaystyle{= \frac{3(3)(2) + 3(3)}{2(2) + 5}}[/latex][latex]\displaystyle{= \frac{18 + 9}{4 + 5} = \frac{27}{9} = 3}[/latex]
Example 7.1-c: Evaluating Algebraic Expressions with Exponents
Evaluate the following expressions:
- [latex]\displaystyle{\frac{(5x)^2 \times 4y}{50}}[/latex], where [latex]x = 2[/latex] and [latex]y = 3[/latex]
- [latex]2(x^2 + 3x) - 5y[/latex], where [latex]x = 4[/latex] and [latex]y = -3[/latex]
Solution
- [latex]\displaystyle{\frac{(5x)^2 \times 4y}{50}}[/latex] Substituting [latex]x = 2[/latex] and [latex]y = 3[/latex],[latex]\displaystyle{= \frac{[5(2)]^2 \times 4(3)}{50}}[/latex][latex]\displaystyle{= \frac{10^2 \times 12}{50} = \frac{100 \times 12}{50} = 24}[/latex]
- [latex]2(x^2 + 3x) - 5y[/latex] Substituting [latex]x = 4[/latex] and [latex]y = -3[/latex],[latex]= 2[(4)^2 + 3(4)] - 5(-3)[/latex][latex]= 2(16 + 12) + 15 = 56 + 15 = 71[/latex]
7.1 Exercises
Answers to the odd-numbered problems are available at the end of the textbook.
For problems 1 and 2, translate the written statements into algebraic expressions.
- a. Three less than twice a number.
b. Two times a number divided by five.
c. Twenty-five increased by three times a number. - a. Seven less than four times a number.
b. Fifteen divided by three times a number.
c. Twenty increased by twice a number.
For problems 3 to 6, (a) identify the number of terms in each expression, (b) identify the constant term (if applicable), and (c) state the coefficients of each of the variable terms.
- a. [latex]3x^2 + 7xy - 4y[/latex]
b. [latex]x^2 - 5x[/latex]
c. [latex]9xy + 7x - 6y + 2[/latex] - a. [latex]-x^2 + 9xy + y + 7[/latex]
b. [latex]7xy[/latex]
c. [latex]10x^2 + 5xy - 7y^2[/latex] - a. [latex]5x^2 - 3xy + 5[/latex]
b. [latex]-2y^2 + 3x + 1[/latex]
c. [latex]-2xy^2 - 2x^2y + 7[/latex] - a. [latex]-2y^2 + 3y - 4[/latex]
b. [latex]y^5 - 2y^7 - 2[/latex]
c. [latex]2x^3 - 3x^2 + 1[/latex]
For problems, 7 to 10, identify any like terms in the expressions.
- a. [latex]12A + 4B - 7A - B[/latex]
b. [latex]6x + 8y - 5x - 3y + 7[/latex] - a. [latex]6B + 8A - A - 2B[/latex]
b. [latex]14 - 3x + 10y + 4y[/latex] - a. [latex]-2x + 5x - 12x + 8 + 7y - 3[/latex]
b. [latex]6xy^2 - 2x^2y - 4x^2 + 2xy^2 + 3x^2y + 2x^2 + 4[/latex] - a. [latex]3 + 6x - 20x + 8y + 8y + 5x + 12[/latex]
b. [latex]3x^2y - 12xy^2 - 6x^2y - 5xy - 2xy - 4xy^2[/latex]
For problems, 11 to 14, evaluate the expressions.
- [latex]2a + 14b - 12c + 2[/latex], where [latex]a = 3[/latex], [latex]b = 2[/latex], [latex]c = 1[/latex]
- [latex]x + 2y - 13z + 1[/latex], where [latex]x = 5[/latex], [latex]y = 8[/latex], [latex]z = 2[/latex]
- [latex]3x^2 - 2x[/latex], where [latex]x = 5[/latex]
- [latex]2a^2 + a[/latex], where [latex]a = 15[/latex]
For problems, 15 to 18, evaluate the expressions, given x = 2 and y = 3.
- a. [latex]\displaystyle{\frac{19x - 5y}{9}}[/latex]
b. [latex]x^2 + 6x + 8[/latex] - a. [latex]\displaystyle{\frac{7x - 5y}{3}}[/latex]
b. [latex]-x^2 + 10x + 7[/latex] - a. [latex]\displaystyle{\frac{(3x)^2 (5y)}{6y}}[/latex]
b. [latex]-2x^2 + 3x + 8y[/latex] - a. [latex]\displaystyle{\frac{(2x)^2 (2y)}{5y}}[/latex]
b. [latex]4x^2 + 10x - 4y[/latex]
Unless otherwise indicated, this chapter is an adaptation of the eTextbook Foundations of Mathematics (3rd ed.) by Thambyrajah Kugathasan, published by Vretta-Lyryx Inc., with permission. Adaptations include supplementing existing material and reordering chapters.