6.1 Percents
Percent (per cent or per hundred in the literal meaning) is used to express a quantity out of 100 units and is represented by the symbol '%'.
For example, 5% means 5 per hundred, or 5 out of 100, or [latex]\displaystyle{\frac{5}{100} (5\% = \frac{5}{100} = 0.05)}[/latex].
- 100% means 100 out of 100 (i.e, the whole quantity)
- 75% means 75 out of 100 (i.e., [latex]\displaystyle{\frac{75}{100} = \frac{3}{4}}[/latex] or 0.75)
- 50% means 50 out of 100 (i.e., [latex]\displaystyle{\frac{50}{100} = \frac{1}{2}}[/latex] or 0.50)
- 25% means 25 out of 100 (i.e., [latex]\displaystyle{\frac{25}{100} = \frac{1}{4}}[/latex] or 0.25)
Note: A percent greater than 100 is typically expressed as a comparison to the original amount, rather than as parts of a whole.
For example, 200% means 2 times (or double, or twice) the whole quantity; although technically correct, it is not meaningful to say 200% means 200 out of 100 (since the total number of parts exceeds the whole). Similarly, 350% means [latex]\displaystyle{3\frac{1}{2}}[/latex] times the whole quanity.
Relationship Among Percents, Fractions, and Decimal Numbers
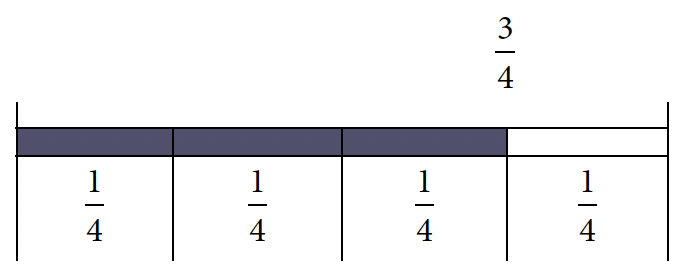
Fractions and decimal numbers can be converted to percents and vice-versa. For example, 3 out of 4 equal parts of a quantity can be represented as a fraction, decimal number, or in percent form, as follows:
As a fraction, it is [latex]\displaystyle{\frac{3}{4}}[/latex].
As a decimal, it is 0.75.
As a percent, it is 75%.
In day-to-day business, percents are commonly used to represent interest rates, sales, discounts, commissions, comparison of changes in quantity, etc. However, in actual calculations, fractions or decimal equivalents are used. Therefore, it is necessary to know the methods for converting from one form to the other.
Converting Percents to Decimal Numbers
If the percent is a whole number or a decimal number, remove the '%' sign and move the decimal point two places to the left. This is the same as dividing the number by 100 and removing the '%' sign.
For example,
- To convert 45% to a decimal number, 45% = 45.0. Remove the % sign and move the decimal point two places to the left.= 0.45. This is the same as [latex]\displaystyle{\frac{45\%}{100\%} = 0.45}[/latex]. Therefore 45% = 0.45.
- To convert 0.38% to a decimal number, 0.38% = 0.38. Remove the % sign and move the decimal point two places to the left. = 0.0038. This is the same as [latex]\displaystyle{\frac{0.38\%}{100\%} = 0.0038}[/latex]. Therefore 0.38% = 0.0038.
If the percent is a fraction or a mixed number, change it to its decimal equivalent and follow the steps as shown above.
For example,
- To convert [latex]\displaystyle{2\frac{1}{2}\%}[/latex] to a decimal number, [latex]\displaystyle{2\frac{1}{2}\% = 2.5\%}[/latex]. Convert the mixed number to a decimal number.= 2.5. Remove the % sign and move the decimal point two places to the left = 0.025. This is the same as [latex]\displaystyle{\frac{2.5\%}{100\%} = 0.025}[/latex]. Therefore [latex]\displaystyle{2\frac{1}{2}\% = 0.025}[/latex].
Example 6.1-a: Converting Percents to Decimal Numbers
Convert each percent to its equivalent decimal number.
- [latex]85\%[/latex]
- [latex]\displaystyle{5\frac{1}{4}\%}[/latex]
- [latex]20.75\%[/latex]
- [latex]225\%[/latex]
- [latex]\displaystyle{\frac{2}{3}\%}[/latex]
Solution
- [latex]85\% = 85.0\% = 85.0 = 0.85[/latex]
- [latex]\displaystyle{5\frac{1}{4}\% = 5.25\% = 5.25 = 0.0525}[/latex]
- [latex]20.75\% = 20.75 = 0.2075[/latex]
- [latex]225\% = 225.0\% = 225.0 = 2.25[/latex]
- [latex]\displaystyle{\frac{2}{3}\% = 0.666666...\% = 0.\overline{6}\% = 0.\overline{6} = 0.00\overline{6}}[/latex]
Converting Decimal Numbers to Percents
To convert a decimal number or a whole number to a percent, move the decimal point two places to the right and insert the '%' sign. This is the same as multiplying the number by 100 and inserting the '%' sign.
For example,
- To convert 0.35 to a percent, 0.35 = 0.35%. Move the decimal point two places to the right and insert the % sign.= 35%. This is the same as [latex]0.35 \times 100\% = 35\%[/latex]. Therefore 0.35 = 35%.
- To convert 5 to a percent, 5 = 5.00%. Move the decimal point two places to the right and insert the % sign.= 500%. This is the same as [latex]5 \times 100\% = 500\%[/latex]. Therefore, 5 = 500%.
Example 6.1-b: Converting Decimal Numbers to Percents
Convert each decimal number to its equivalent percent.
- [latex]0.45[/latex]
- [latex]0.03[/latex]
- [latex]5.25[/latex]
- [latex]0.002[/latex]
Solution
- [latex]0.45 = 0.45\% = 45\%[/latex]
- [latex]0.03 = 0.03\% = 3\%[/latex]
- [latex]5.25 = 5.25\% = 525\%[/latex]
- [latex]0.002 = 0.002\% = 0.2\%[/latex]
Example 6.1-c: Application of Converting from Decimal to Percent
If Alexander earns three times the amount that Emma earns, what percent is Alexander's earnings compared to Ema's earnings?
Solution
Here, '3 times' when converted to a percent [latex]= 3 \times 100\% = 300\%[/latex].
Therefore, Alexander's earnings are 300% of Emma's.
Note: This also means that Alexander earns 200% more than Emma. It is important not to confuse these two statements!
Converting Percents to Fractions
If the percent is a whole number, remove the percent sign and divide by 100 (or multiply by [latex]\displaystyle{\frac{1}{100}}[/latex]). Reduce the resulting fraction to its lowest terms.
For example, to convert 60% to a fraction in its lowest terms:
[latex]\displaystyle{60\% = \frac{60}{100}}[/latex]
Reduce the fraction to its lowest terms.
[latex]\displaystyle{= \frac{3}{5}}[/latex]
Therefore, [latex]\displaystyle{60\% = \frac{3}{5}}[/latex].
If the percent is a decimal number, remove the percent sign and divide by 100; eliminate the decimal in the numerator of the resulting fraction by multiplying both the numerator and denominator by an appropriate power of 10. Reduce the fraction to its lowest terms.
For example, to convert [latex]42.5\%[/latex] to a fraction:
[latex]\displaystyle{42.5\% = \frac{42.5}{100}}[/latex]
Eliminate the decimal in the numerator by multiplying both the numerator and the denominator by 10.
[latex]\displaystyle{= \frac{425}{1,000}}[/latex]
Reduce the fraction to its lowest terms.
[latex]\displaystyle{= \frac{17}{40}}[/latex]
Therefore, [latex]\displaystyle{42.5\% = \frac{17}{40}}[/latex].
If the percent is a fraction or a mixed number, either convert it to its decimal equivalent and follow the steps outlined above, or convert it to an improper fraction (if required), remove the percent sign, and multiply the fraction by [latex]\displaystyle{\frac{1}{100}}[/latex].
For example, to convert [latex]\displaystyle{6\frac{1}{2}\%}[/latex] to a fraction,
Method 1:
By converting it to its decimal equivalent.
[latex]\displaystyle{6\frac{1}{2}\% = 6.5\%}[/latex]
Remove the percent sign and divide by 100.
[latex]\displaystyle{= \frac{6.5}{100}}[/latex]
Eliminate the decimal in the numerator by multiplying both the numerator and the denominator by 10.
[latex]\displaystyle{= \frac{65}{1,000}}[/latex]
Reduce the fraction to its lowest terms.
[latex]\displaystyle{= \frac{13}{200}}[/latex]
Method 2:
By converting it to its improper fractional equivalent.
[latex]\displaystyle{6\frac{1}{2}\% = \frac{13}{2}\%}[/latex]
Remove the percent sign and multiply the fraction by [latex]\displaystyle{\frac{1}{100}}[/latex].
[latex]\displaystyle{= \frac{13}{2} \times \frac{1}{100}}[/latex]
Simplify.
[latex]\displaystyle{= \frac{13}{200}}[/latex]
Therefore, [latex]\displaystyle{6\frac{1}{2}\% = \frac{13}{200}}[/latex].
Example 6.1-d: Converting Percents to Fractions
Convert each percent to its equivalent fraction or mixed number and simplify to lowest terms.
- [latex]45\%[/latex]
- [latex]\displaystyle{8\frac{1}{3}\% }[/latex]
- [latex]6.25\%[/latex]
- [latex]175\%[/latex]
- [latex]\displaystyle{\frac{1}{5}\%}[/latex]
Solution
- [latex]\displaystyle{45\% = \frac{45}{100} = \frac{9}{20}}[/latex]
- [latex]\displaystyle{8\frac{1}{3}\% = \frac{25}{3}\% = \frac{25}{3} \times \frac{1}{100} = \frac{1}{3} \times \frac{1}{4} = \frac{1}{12}}[/latex]
- [latex]\displaystyle{6.25\% = \frac{6.25}{100} = \frac{6.25}{100} \times \frac{100}{100} = \frac{625}{10,000} = \frac{1}{16}}[/latex]
- [latex]\displaystyle{175\% = \frac{175}{100} = \frac{7}{4} = 1\frac{3}{4}}[/latex]
- [latex]\displaystyle{\frac{1}{5}\% = \frac{1}{5} \times \frac{1}{100} = \frac{1}{500}}[/latex]
Converting Fractions or Mixed Numbers to Percents
To convert a fraction or a mixed number to a percent, first convert the fraction or the mixed number to a decimal number. Then, convert the decimal number to a percent by moving the decimal point two places to the right and inserting the '%' sign. This is the same as multiplying the decimal by 100 and inserting the '%' sign.
For example,
- To convert [latex]\displaystyle{\frac{3}{8}}[/latex] to a percent, [latex]\displaystyle{\frac{3}{8} = 0.375}[/latex]. Convert the fraction to its decimal equivalent.[latex]\displaystyle{= 0.375\%}[/latex]. Convert the decimal to percent, by moving the decimal point two places to the right and inserting the % sign. [latex]\displaystyle{= 37.5\%}[/latex]. This is the same as [latex]0.375 \times 100\% = 37.5\%[/latex]. Therefore [latex]\displaystyle{\frac{3}{8} = 37.5\%}[/latex].
- To convert [latex]\displaystyle{5\frac{1}{2}}[/latex] to a percent, [latex]\displaystyle{5\frac{1}{2} = 5.50}[/latex]. Convert the fraction to its decimal equivalent. [latex]\displaystyle{= 5.50\%}[/latex]. Convert the decimal to percent, by moving the decimal point two places to the right and inserting the % sign. [latex]\displaystyle{= 550\%}[/latex]. This is the same as [latex]5.50 \times 100\% = 550\%[/latex]. Therefore [latex]\displaystyle{5\frac{1}{2} = 550\%}[/latex].
Example 6.1-e: Converting Fractions or Mixed Numbers to Percents
Convert each of the following fractions to its equivalent percent.
- [latex]\displaystyle{\frac{3}{25}}[/latex]
- [latex]\displaystyle{5\frac{1}{4}}[/latex]
- [latex]\displaystyle{\frac{18}{5}}[/latex]
- [latex]\displaystyle{\frac{1}{200}}[/latex]
Solution
- [latex]\displaystyle{\frac{3}{25} = 0.12 = 0.12\% = 12\%}[/latex]
- [latex]\displaystyle{5\frac{1}{4} = 5.25 = 5.25\% = 525\%}[/latex]
- [latex]\displaystyle{\frac{18}{5} = 3.60 = 3.60\% = 360\%}[/latex]
- [latex]\displaystyle{\frac{1}{200} = 0.005 = 0.005\% = 0.5\%}[/latex]
Example 6.1-f: Application of Converting from Fractions to Percents
Peter and Angela study Business Mathematics but at different colleges. Peter scored 46 out of 60 on his final exam, while Angela scored 63 out of 75 on her exam. Who received a better grade on their exam?
Solution
It is not possible to answer the question by simple observation, because Peter's score is expressed out of 60, while Angela's score is expressed out of 75. To compare their scores, we can convert them to their percent equivalents, as shown below:
Peter's score: [latex]\displaystyle{\frac{46}{60} = 0.766666… = 76.67\%}[/latex]
Angela's score: [latex]\displaystyle{\frac{63}{75} = 0.84 = 84\%}[/latex]
Therefore, Angela received a better grade than Peter on the exam.
Example 6.1-g: Comparing Fractions and Percents
Out of 54 students in Class A, 43 students passed the final exam. In Class B, 78% of the students passed the final exam. Which class had the better pass rate?
Solution
Class A:
Fraction of students passed [latex]\displaystyle{= \frac{43}{54}}[/latex]
Percent of students passed [latex]\displaystyle{= \frac{43}{54} \times 100\%}[/latex]
[latex]= 0.796296... \times 100\%[/latex]
[latex]= 79.63\%[/latex]
Class B:
Percent of students passed [latex]= 78\%[/latex]
Therefore, Class A had a better pass rate.
Solving Percent Problems
Many methods may be used to solve percent problems. Described below are three common methods:
Method 1: Formula Method
Every percent problem will contain three variables: B, P, and R.
Base (B): Whole quantity or value (100%). It usually follows the word 'of', or 'percent of'.
Portion (P): Portion of the whole quantity or value (i.e., portion of the base).
Rate (R): Relationship between the base and portion, usually expressed as a percent. It usually carries the percent sign ( % ) or the word 'percent'.
Every percent statement can be expressed as: P is R% of B. The value of R is used as a decimal or fractional equivalent in calculations.
The relationship between these variables can be expressed as follows:
Portion = Rate × Base
Or
Formula 6.1: Portion
P = R × B
Rearranging, we obtain [latex]\displaystyle{R = \frac{P}{B}}[/latex] and [latex]\displaystyle{B = \frac{P}{R}}[/latex].
Therefore, if any two of these quantities are known, then the third quantity can be calculated.
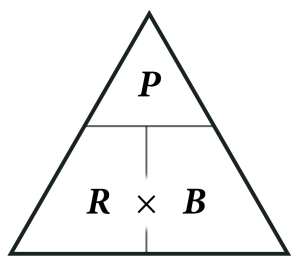
P, R, B triangle
Here is a triangle that can be used to help in rearranging the formula P = R × B to solve for the variable R or B.
Variables beside each other at the bottom are multiplied, (R × B, as shown).
Variable P is divided by the variables at the bottom.
Cover the variable for which you want to solve to see the new formula.
For example, if you want to solve for R, the formula can be found by covering R and reading the remaining variables in the triangle, to obtain [latex]\displaystyle{R = \frac{P}{B}}[/latex]
Method 2: Algebraic Method
Solving problems using algebraic methods involve forming an equation for an unknown 'x' and then solving for 'x'. In this method, we assume that the unknown is 'x', and form equation(s) for the given problem (or statement) using key words to represent certain arithmetic operations.
The following table shows key words and phrases that are commonly used to indicate various arithmetic operations.
| Operation | Key Words or Phrases |
|---|---|
| Addition (+) | Add, sum, total, and, plus, more than, increased by, appreciate, rise |
| Subtraction (−) | Subtract, difference, minus, less than, decreased by, depreciate, fall |
| Multiplication (× or () or ·) | Multiply, product, times, of |
| Division (÷ or /) | Divide, ratio, divided by, quotient, per |
| Equal (=) | Is, was, gives, given by |
| Unknown value (denoted by a variable, such as 'x') | What, how much |
For example, we can use these key words to form the algebraic equations for the following:
- What percent of 200 is 60? x% × 200 = 60
- $52 is 13% of what amount? $52 = 13%(x)
- 40% of what amount is $280? 40%(x) = $280
- How much is 2% of 75? x = 2% × 75
Method 3: Ratio-Proportion Method
The whole amount or quantity is represented by 100% and is known as the base (B). The portion (P) is a part of the base and it forms a percent, or rate (R%), of the base. Thus, in the ratio proportion method, we first identify the base, portion, and rate in the problem, then solve for the unknown using the following proportion equation:
Portion : Base = Rate : 100%
[latex]P : B = R\% : 100\%[/latex]
[latex]\displaystyle{\frac{P}{B} = \frac{R\%}{100\%}}[/latex]
[latex]\displaystyle{\frac{P}{B} = \frac{R}{100}}[/latex]
Example 6.1-h: Calculating the Portion of a Whole Quantity
What is 75% of $250? (Or, 75% of $250 is how much?)
Solution
Method 1: Using the Formula Method
R% = 75% (value with % sign); i.e., R = 0.75
B = $250 (value that follows the word 'of')
P = ? (the other value)
Using Formula 6.1,
P = R × B
Substituting values for R and B, P = 0.75 × 250.00
Simplifying,
= $187.50
Method 2: Using the Algebraic Method
What is 75% of $250?
x = 75% × 250.00
Expressing the percent as a decimal,
x = 0.75 × 250.00
Simplifying,
= $187.50
Method 3: Using the Ratio-Proportion Method
Here, the whole amount of $250 is the base and is represented by 100%. 75% is a portion of the base, as illustrated:
Portion : Base = Rate : 100%
[latex]P : B = R\% : 100\%[/latex]
[latex]P : \$250 = 75\% : 100\%[/latex]
[latex]\displaystyle{\frac{P}{\$250} = \frac{75\%}{100\%}}[/latex]
[latex]\displaystyle{\frac{P}{250.00} = \frac{75}{100}}[/latex]
Cross-multiplying,
[latex]100P = 250.00 \times 75[/latex]
Solving for P,
[latex]\displaystyle{P = \frac{250.00 \times 75}{100}}[/latex]
Simplifying,
= $187.50
Therefore, 75% of $250.00 is $187.50.
Note: The following examples use the formula method; however, you can solve them using any of the three methods described above.
Example 6.1-i: Calculating Portion When Rate is More Than 100%
What is 150% of 200?
Solution
R% = 150% (value with % sign); i.e., R = 1.50
B = 200 (value that follows the word 'of')
P = ? (the other value)
Using Formula 6.1,
P = R × B
Substituting values for R and B,
P = 1.50 × 200
Simplifying,
= 300
Therefore, 150% of 200 is 300.
Example 6.1-j: Calculating Rate When Portion and Base are Known
What percent of $775 is $1,250? (Or, $1,250 is what percent of $775?)
Solution
B = $775 (value that follows the word 'of')
P = $1,250 (the other value)
R = ? (value for the word 'percent')
Using Formula 6.1,
P = R × B
Rearranging for R,
[latex]\displaystyle{R = \frac{P}{B}}[/latex]
Substituting values for P and B,
[latex]\displaystyle{R = \frac{1,250.00}{775.00}}[/latex]
Simplifying,
[latex]R = 1.612903...[/latex]
Converting the decimal to a percent,
[latex]R\% = 1.612903... \times 100\%[/latex]
[latex]= 161.29\%[/latex]
Therefore, 161.29% of $775.00 is $1,250.00.
Note: It is tempting to treat $1,250 as the base since it is the larger value. However, in this question $775 is the base since it follows the word 'of'. This illustrates the importance of reading these types of questions carefully!
Example 6.1-K: Calculating Base When Portion and Rate are Known
50% of what number is 200?
Solution
R% = 50% (value with % sign); i.e., R = 0.50
P = 200 (the other value)
B = ? (value that follows the word 'of')
Using Formula 6.1,
P = R × B
Rearranging for B,
[latex]\displaystyle{B = \frac{P}{R}}[/latex]
Substituting values for P and R,
[latex]\displaystyle{B = \frac{200}{0.50}}[/latex]
Simplifying,
[latex]= 400[/latex]
Therefore, 50% of 400 is 200.
Example 6.1-l: Application Problem with a Fractional Rate
Sandra owns [latex]\displaystyle{25\frac{1}{3}\%}[/latex] of a web development company. If the company is valued at $180,000 what is the value of Sandra's ownership in the company?
Solution
R% [latex]\displaystyle{ = 25\frac{1}{3}\%}[/latex] (value with % sign) [latex]= 25.333333...%[/latex]; i.e., [latex]R = 0.253333...[/latex]
B = $180,000 (the whole value)
P ? (the other value)
Using Formula 6.1,
P = R × B
Substituting values for R and B,
= 0.253333… × 180,000.00
Simplifying,
= $45,600.00
Alternatively, instead of performing calculations with repeating decimals, this question can be solved by converting the percent into a fraction:
R% [latex]\displaystyle{ = 25\frac{1}{3}\%}[/latex]
Converting the mixed number into an improper fraction,
[latex]\displaystyle{ = \frac{76}{3}\%}[/latex]
Converting the percent into a fraction,
[latex]\displaystyle{R = \frac{76}{3} \times \frac{1}{100}}[/latex]
[latex]\displaystyle{= \frac{76}{300}}[/latex]
Using Formula 6.1,
P = R × B
Substituting values for R and B,
[latex]\displaystyle{= \frac{76}{300} \times 180,000.00}[/latex]
Simplifying,
[latex]= \$45,600.00[/latex]
Therefore, the value of Sandra's ownership in the company is $45,600.00.
6.1 Exercises
For problems 1 to 18, calculate the missing values (indicated with a question mark) in the tables below.
-
Question Percents Decimals Fractions (or mixed numbers) in lowest terms a. 75% ? ? b. ? 0.30 ? c. ? ? [latex]\displaystyle{\frac{1}{4}}[/latex] -
Question Percents Decimals Fractions (or mixed numbers) in lowest terms a. 50% ? ? b. ? 0.70 ? c. ? ? [latex]\displaystyle{\frac{1}{5}}[/latex] -
Question Percents Decimals Fractions (or mixed numbers) in lowest terms a. 5% ? ? b. ? 0.2 ? c. ? ? [latex]\displaystyle{\frac{3}{5}}[/latex] -
Question Percents Decimals Fractions (or mixed numbers) in lowest terms a. 2% ? ? b. ? 0.8 ? c. ? ? [latex]\displaystyle{\frac{3}{8}}[/latex] -
Question Percents Decimals Fractions (or mixed numbers) in lowest terms a. 150% ? ? b. ? 0.175 ? c. ? ? [latex]\displaystyle{\frac{12}{25}}[/latex] -
Question Percents Decimals Fractions (or mixed numbers) in lowest terms a. 225% ? ? b. ? 0.225 ? c. ? ? [latex]\displaystyle{\frac{7}{20}}[/latex] -
Question Percents Decimals Fractions (or mixed numbers) in lowest terms a. 12.5% ? ? b. ? 0.05 ? c. ? ? [latex]\displaystyle{4\frac{1}{2}}[/latex] -
Question Percents Decimals Fractions (or mixed numbers) in lowest terms a. 7.5% ? ? b. ? 0.03 ? c. ? ? [latex]\displaystyle{3\frac{3}{4}}[/latex] -
Question Percents Decimals Fractions (or mixed numbers) in lowest terms a. 0.6% ? ? b. ? 0.005 ? c. ? ? [latex]\displaystyle{4\frac{3}{5}}[/latex] -
Question Percents Decimals Fractions (or mixed numbers) in lowest terms a. 0.8% ? ? b. ? 0.003 ? c. ? ? [latex]\displaystyle{1\frac{1}{5}}[/latex] -
Question Percents Decimals Fractions (or mixed numbers) in lowest terms a. 0.05% ? ? b. ? 0.0025 ? c. ? ? [latex]\displaystyle{1\frac{1}{8}}[/latex] -
Question Percents Decimals Fractions (or mixed numbers) in lowest terms a. 0.08% ? ? b. ? 0.075 ? c. ? ? [latex]\displaystyle{2\frac{3}{8}}[/latex] -
Question Percents Decimals Fractions (or mixed numbers) in lowest terms a. [latex]\displaystyle{\frac{3}{5}\%}[/latex] ? ? b. ? 1.08 ? c. ? ? [latex]\displaystyle{\frac{3}{55}}[/latex] -
Question Percents Decimals Fractions (or mixed numbers) in lowest terms a. [latex]\displaystyle{\frac{3}{8}\%}[/latex] ? ? b. ? 2.04 c. ? ? [latex]\displaystyle{\frac{22}{75}}[/latex] -
Question Percents Decimals Fractions (or mixed numbers) in lowest terms a. [latex]\displaystyle{1\frac{3}{4}\%}[/latex] ? ? b. ? 2.025 ? c. ? ? [latex]\displaystyle{\frac{1}{400}}[/latex] -
Question Percents Decimals Fractions (or mixed numbers) in lowest terms a. [latex]\displaystyle{2\frac{3}{4}\%}[/latex] ? ? b. ? 1.075 ? c. ? ? [latex]\displaystyle{\frac{1}{250}}[/latex] -
Question Percents Decimals Fractions (or mixed numbers) in lowest terms a. [latex]\displaystyle{6\frac{1}{2}\%}[/latex] ? ? b. ? 2.5 ? c. ? ? [latex]\displaystyle{\frac{4}{25}}[/latex] -
Question Percents Decimals Fractions (or mixed numbers) in lowest terms a. [latex]\displaystyle{10\frac{3}{5}\%}[/latex] ? ? b. ? 7.5 ? c. ? ? [latex]\displaystyle{\frac{13}{50}}[/latex]
For the following problems, express the answers rounded to two decimal places, wherever applicable.
For problems 19 to 48, calculate the value.
- a. 20% of 350
b. 12.5% of 800 - a. 45% of 180
b. 2.5% of 960 - a. 0.25% of 75
b. [latex]\displaystyle{\frac{1}{4}\%}[/latex] of 200 km - a. 0.755% of 120
b. [latex]\displaystyle{\frac{1}{8}\%}[/latex] of 450 km - a. 130% of 40
b. [latex]\displaystyle{5\frac{1}{3}\%}[/latex] of $1,000 - a. 285% of 110
b. [latex]\displaystyle{12\frac{3}{4}\%}[/latex] of $1,260 - What is 2.5% of 80?
- What is 40% of 160?
- [latex]\displaystyle{8\frac{1}{4}\%}[/latex] of $200 is how much?
- [latex]\displaystyle{25\frac{3}{4}\%}[/latex] of $2,680 is how much?
- How much is [latex]\displaystyle{\frac{1}{4}\%}[/latex] of $108?
- How much is [latex]\displaystyle{\frac{3}{4}\%}[/latex] of 350 kg?
- What number is 125% of 6?
- What number is 250% of 12?
- 12 is what percent of 30?
- 18 is what percent of 40?
- What percent of 4 is 16?
- What percent of 9 is 45?
- What percent of 220 is 100?
- What percent of 22.10 is 110.50?
- 280 metres is what percent of a kilometre?
- 180 grams is what percent of 3 kilograms?
- 400 is 50% of what number?
- 225 is 25% of what number?
- 15% of what amount is $27.90?
- 30% of what amount is 708?
- 120% of what amount is 156?
- 215% of what amount is 258?
- $16.50 is 0.75% of what amount?
- $16.40 is 0.5% of what amount?
- How much tax was charged on a table that costs $250, if the tax rate is 13%?
- The monthly gross salary of an employee is $6,250. 26% of the salary was deducted for taxes. How much money was deducted for taxes?
- 5% of the commission on sales was $1,250. How much was the sales amount?
- 3% interest on a loan was $210. How much was the loan?
- In a survey of 450 people, 117 responded 'yes'. What percent of the people surveyed responded 'no'?
- 144 out of 600 students took Business Mathematics. What percent of students did not take the course?
- A company that makes games sets sales targets at $280,000 per year for each of its salespeople. If Amanda, an excellent salesperson, achieved 250% of her target this year, calculate her sales for the year.
- If the population of Canada was estimated to be 36,910,000 in May 2018, and the population of Ontario was estimated to be [latex]\displaystyle{38\frac{1}{4}\%}[/latex] of Canada's population, calculate the estimated population of Ontario.
- When there was a boom in the real estate market, Lucy sold her property for $410,440, which was 130% of the amount she originally paid. Calculate the amount she originally paid for the property.
- Ronald, an investment banker sold his shares for $18,568.50 when there was a boom in the stock market. Calculate the amount he paid for the shares if his selling price was 180.65% of the amount he paid for the shares originally.
- Evan, a business development representative of a leading pharmaceutical firm, took his client out for a dinner that cost $180.75 before taxes. If the tax was $23.50, calculate the tax rate.
- A leading information technology company donated $87,790 out of its 2017 fiscal revenue of $17,558,643 towards socially-responsible causes. What percent of its revenue did it contribute towards these causes?
- Neel Plastics Manufacturing Corporation targets to obtain $120,000 of funding from their investors to purchase new machinery. If they were only able to obtain 25.5% of their total target, calculate the amount of money that is yet to be received.
- Pamela and Martha run a business that made a profit of $12,750. As Pamela invested a higher amount in the business, she received 57.5% of the profits and Martha received the remaining. Calculate Martha's share of the profit, in dollars.
Unless otherwise indicated, this chapter is an adaptation of the eTextbook Foundations of Mathematics (3rd ed.) by Thambyrajah Kugathasan, published by Vretta-Lyryx Inc., with permission. Adaptations include supplementing existing material and reordering chapters.