5.1 Ratios
A ratio is a comparison or relationship between two or more quantities with the same units. Therefore, ratios are not expressed with units.
For example, if Andy (A) invested $5,000 and Barry (B) invested $4,000 in a business, the comparison of A's investment to B's investment in the same order is known as the ratio of their investments.
Expressing Ratios
Expressing a Ratio of Two Quantities
When comparing two quantities, there are different ways to express the ratio. In the example above, the ratio of A's investment to B's may be expressed in any of the following forms:
5,000 to 4,000 (separate the quantities using the word 'to')
5,000 : 4,000 (using a colon and read as '5,000 is to 4,000')
[latex]\displaystyle{\frac{5,000}{4,000}}[/latex] (as a fraction and read as '5,000 over 4,000')
In the above example, the decimal equivalent of the fraction [latex]\displaystyle{\frac{5,000}{4,000}}[/latex] is 1.25; therefore, we can state
that “A's invesment is 1.25 times B's investment”.
Note: When representing a ratio as a fraction, if the denominator is 1, the denominator (1) must still be written. For example, if the ratio of two quantities is [latex]\displaystyle{\frac{3}{1}}[/latex], then it is incorrect to say that the ratio is 3. It should be stated as [latex]\displaystyle{\frac{3}{1}}[/latex] or 3 : 1.
Expressing a Ratio of More than Two Quantities
When comparing more than two quantities, the ratio is expressed using colons.
For example, if A's investment is $5,000, B's investment is $4,000, and C's investment is $1,000 in a business, then the ratio of their investments, respectively, is expressed as:
5,000 : 4,000 : 1,000
Terms of a Ratio
The quantities in a ratio are known as the terms of the ratio.
For example, the terms of the ratio 5 : 7 : 19 are 5, 7, and 19.
Equivalent Ratios
When all the terms of the ratio are multiplied by the same number or divided by the same number, the result will be an equivalent ratio.
For example, when the terms of the ratio 12 : 15 are multiplied by 2, we obtain an equivalent ratio of 24 : 30.
12 : 15
12 × 2 : 15 × 2
24 : 30
When the terms of the ratio 12 : 15 are divided by the common factor 3, we obtain the equivalent ratio of 4 : 5.
12 : 15
12 ÷ 3 : 15 ÷ 3
4 : 5
Therefore, the ratios 12 : 15, 24 : 30, and 4 : 5 are equivalent ratios.
[latex]24:30 = 12:15 = 4:5[/latex]
[latex]\dfrac{24}{30} = \dfrac{12}{15} = \dfrac{4}{5}[/latex]
Reducing a Ratio to its Simplest or Lowest Terms
Comparisons are easier when ratios are reduced to their lowest terms. When all the terms of a ratio are integers, the ratio can be reduced to its lowest terms by dividing all the terms by their common factors.
For example, if A earns $3,000, B earns $4,500, and C earns $6,000, then the equivalent ratio of their earnings reduced to its lowest terms is calculated as follows:
A : B : C
3,000 : 4,500 : 6,000 Dividing each term by the common factor 100,
30 : 45 : 60 Dividing each term by the common factor 15,
2 : 3 : 4 The ratio is now in its lowest terms.
By reducing the ratio to lowest terms, we can say that the earnings of A, B, and C are in the ratio of 2 : 3 : 4.
When two ratios are equivalent, they result in the same answer when reduced to lowest terms.
Example 5.1-a: Determining Equivalent Ratios
Determine whether the given pairs of ratios are equivalent by reducing them to lowest terms.
- 18 : 12 and 12 : 8
- 20 : 24 and 15 : 20
Solution
- 18 : 1218 ÷ 6 : 12 ÷ 63 : 212 : 812 ÷ 4 : 8 ÷ 43 : 2
Therefore, the ratios 18 : 12 and 12 : 8 are equivalent. - 20 : 2420 ÷ 4 : 24 ÷ 45 : 615 : 2015 ÷ 5 : 20 ÷ 53 : 4
Therefore, the ratios 20 : 24 and 15 : 20 are not equivalent.
Reducing Ratios When One or More of the Terms of the Ratio Are Fractions
To reduce a ratio with fractions, first convert all the terms to integers by multiplying all the terms by the least common denominator, and then reduce to lowest terms.
For example,
[latex]\displaystyle{\frac{2}{3}}[/latex] : [latex]\displaystyle{\frac{4}{5}}[/latex] : 2 Multiplying each term by the least common denominator 15,
10 : 12 : 30
Dividing each term by the common factor 2,
5 : 6 : 15
Reducing Ratios When One or More of the Terms of the Ratio Are Decimal Numbers
To reduce a ratio with decimal numbers, first convert all the terms to integers by moving the decimal point of all the terms to the right by the same number of places, and then reduce to lowest terms.
For example,
2.25 : 3.5 : 5
Moving the decimal point of each term two places to the right,
225 : 350 : 500
Dividing each term by the common factor 25,
9 : 14 : 20
Reducing Ratios When the Terms of the Ratio Are a Combination of Fractions and Decimal Numbers
To reduce a ratio with both fractions and decimal numbers, first convert all the fractional terms to integers, and then convert all the decimal terms to integers. Finally, reduce to lowest terms.
For example,
5.8 : [latex]\displaystyle{\frac{9}{2}}[/latex] : 4 Multiplying each term by 2,
11.6 : 9 : 8
Moving the decimal point of each term one place to the right,
116 : 90 : 80
Dividing each term by the common factor 2,
58 : 45 : 40
Reducing Ratios to an Equivalent Ratio Where the Smallest Term is 1
To make the comparison of quantities easier, we can also reduce a ratio to its equivalent ratio where the smallest term is equal to 1, by dividing all the terms by the smallest term.
For example, if the investment amounts of three partners A, B, and C are $35,000, $78,750, and $59,500, respectively, then the equivalent ratio of their investments, where the smallest term is 1, is calculated as follows:
A : B : C
35,000 : 78,750 : 59,500
Dividing each term by the smallest term, 35,000,
1 : 2.25 : 1.7
The ratio is now reduced to its equivalent ratio with the smallest term equal to 1.
By reducing the ratio so that the smallest term is equal to 1, we can state: (i) B's investment is 2.25 times A's investment, and (ii) C's investment is 1.7 times A's investment.
Example 5.1-b: Reducing Ratios to Lowest Terms
Express the following ratios as equivalent ratios in their lowest terms (as whole numbers) and then reduce them to ratios where the smallest term is 1.
- [latex]\displaystyle{2\frac{7}{9} : 3\frac{1}{3} :5}[/latex]
- 2.5 : 1.75 : 0.625
- [latex]\displaystyle{1.25 : \frac{5}{6} : 2}[/latex]
Solution
- [latex]\displaystyle{2\frac{7}{9} : 3\frac{1}{3} :5}[/latex]
Converting the terms with mixed numbers to improper fractions, [latex]\displaystyle{\frac{25}{9} : \frac{10}{3} :5}[/latex]
Multiplying each term by the least common denominator 9, 25 : 30 : 45
Dividing each term by the common factor 5, 5 : 6 : 9
Dividing each term by the smallest term 5, 1 : 1.2 : 1.8
Therefore, [latex]\displaystyle{2\frac{7}{9} : 3\frac{1}{3} :5}[/latex] reduced to its lowest terms is 5 : 6 : 9 and the equivalent ratio where the smallest term is 1 is 1 : 1.2 : 1.8. - 2.5 : 1.75 : 0.6252.5 : 1.75 : 0.625
Moving the decimal point of each term three places to the right, 2,500 : 1,750 : 625
Dividing each term by the common factor 125, 20 : 14 : 5
Dividing each term by the smallest term 5, 4 : 2.8 : 1
Therefore, 2.5 : 1.75 : 0.625 reduced to its lowest terms is 20 : 14 : 5 and the equivalent ratio where the smallest term is 1 is 4 : 2.8 : 1. - [latex]\displaystyle{1.25 : \frac{5}{6} : 2}[/latex]
Multiplying each term by 6,7.5 : 5 : 12
Moving the decimal point of each term one place to the right, 75 : 50 : 120
Dividing each term by the common factor 5,15 : 10 : 24
Dividing each term by the smallest term 10, 1.5 : 1 : 2.4
Therefore, [latex]\displaystyle{1.25 : \frac{5}{6} : 2}[/latex] reduced to its lowest terms is 15 : 10 : 24 and the equivalent ratio where the smallest term is 1 is 1.5 : 1 : 2.4.
Order of a Ratio
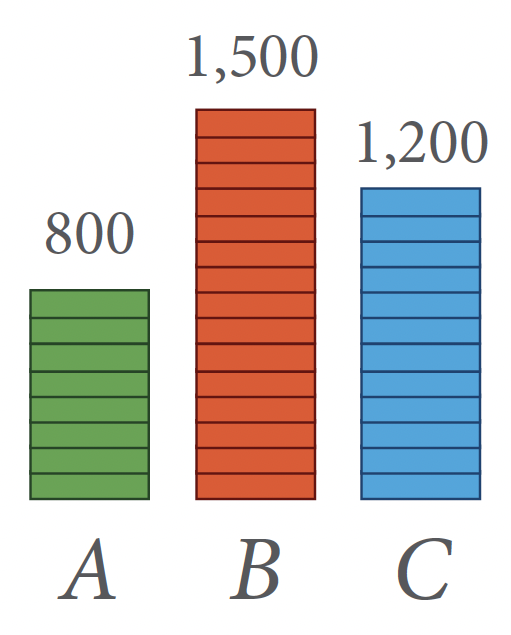
The order of presenting terms in a ratio is important. For example, if A saves $800, B saves $1,500, and C saves $1,200, then the ratio of the savings of A to B to C is:
A : B : C
800 : 1,500 : 1,200 Dividing each term by the common factor 100,
In the previous example, the ratio of the savings of C to B to A is:
C : B : A
1,200 : 1,500 : 800 Dividing each term by the common factor 100,
Notice that C : B : A is not the same as A : B : C.
Ratios compare the numbers in order. The ratio 12 : 15 : 8 expresses a different comparison than the ratio 8 : 15 : 12.
Comparing Quantities
When using ratios to compare quantities of items that have the same kind of measure, the units have to be the same.
For example, the ratio of 45 minutes to 2 hours is not 45 : 2. We are comparing 'time' in both these cases; therefore, the units used have to be the same.
45 minutes : 2 hours
Converting 2 hours to minutes using 1 hour = 60 minutes,
45 minutes : 120 minutes
Dividing by the common factor 15,
3 : 8
Similarly, we determine the ratio of 2.5 kilometres to 3,000 metres as follows:
2.5 km : 3,000 m
Converting km to m using 1 km = 1,000 m,
2,500 m : 3,000 m
Dividing by the common factor 100,
25 : 30
Dividing by the common factor 5,
5 : 6
Example 5.1-c: Comparing Quantities that have the Same Kind of Measure but Different Units
Express each of the following ratios in its simplest form:
- 1.2 L to 800 mL
- 16 weeks to 2 years
Solution
- 1.2 L to 800 mL
Converting 1.2 L to mL using 1 L = 1,000 mL,1,200 mL : 800 mL
Dividing both terms by the common factor 400, 3 : 2
Therefore, the ratio of 1.2 L to 800 mL is 3 : 2. - 16 weeks to 2 years
Converting 2 years to weeks using 1 year = 52 weeks, 16 weeks : 104 weeks
Dividing both terms by the common factor 8,2 : 13
Therefore, the ratio of 16 weeks to 2 years is 2 : 13.
When using ratios to compare quantities of items that have different kinds of measure, the units of measurement of each quantity must be included in the ratio.
For example, when baking a cake, Maggie uses 4 kilograms of flour, 2 litres of water, and 6 eggs.
Therefore, the ratio of flour to water to eggs is,
flour (kg) : water (L) : eggs (number)
4 : 2 : 6
Dividing each term by the common factor 2,
2 : 1 : 3
i.e., 2 kg flour : 1 L water : 3 eggs
Rate, Unit Rate, and Unit Price
Rate
A rate is a special ratio that is used to compare two quantities or amounts that have different kinds of measure. The units of measurement of both quantities are included when expressing a rate.
For example, if a car travels 100 km using 9 L of gas, then the rate of kilometres per litres is 100 km : 9 L. The first term of the ratio is measured in kilometres and the second term is measured in litres. The word 'per' indicates that it is a rate and is usually denoted by a slash “/”. Therefore, 100 km : 9 L is usually written as 100 km per 9 L or 100 km/9 L.
Rates are used in our day-to-day activities such as travelling, working, shopping, etc.
For example,
- travelling 90 kilometres in 1.5 hours: 90 km/1.5 hours
- working 75 hours in 2 weeks: 75 hours/2 weeks
- paying $4.80 for 4 litres of milk: $4.80/4 L
Example 5.1-d: Expressing Rate as a Ratio of Different Units of Measurement
A laser printer printed 88 pages in 6 minutes. Express the rate in lowest terms.
Solution
The unit of the first term is in number of pages and the unit of the second term is in minutes.
88 pages : 6 minutes
Dividing each term by the common factor 2,
44 pages : 3 minutes
This is expressed as a rate as 44 pages/3 minutes.
Therefore, the printing rate is 44 pages/3 minutes.
Unit Rate
Unit rate represents the number of units of the first quantity (or measurement) that corresponds to one unit of the second quantity (or measurement). That is, unit rate is a rate which has a denominator of 1.
Rate can be converted to unit rate simply by dividing the first term by the second term.
For example, a rate of 90 kilometres in 1.5 hours, converted to unit rate:
90 km/1.5 hours
[latex]\displaystyle{= \frac{90 km}{1.5 hours}}[/latex]
= 60 km/hour
Similarly, a rate of 75 hours in 2 weeks, converted to unit rate:
75 hours/2 weeks
[latex]\displaystyle{= \frac{75 hours}{2 weeks}}[/latex]
= 37.5 hours/week
Example 5.1-e: Calculating Unit Rate
A car travelled 300 kilometres in 5 hours. Calculate its average speed in km/h.
Solution
The rate of speed is 300 kilometres in 5 hours.
[latex]\displaystyle{= \frac{300 km}{5 h}}[/latex]
Dividing the first term by the second term to obtain the unit rate,
= 60 km/h
Therefore, the average rate of speed is 60 kilometres per hour, or 60 km/h.
Example 5.1-f: Calculating Hourly Rate of Pay
Peter worked 9 hours and earned $247.50. Calculate his hourly rate of pay.
Solution
The rate of pay is $247.50 for 9 hours.
[latex]\displaystyle{= \frac{\$247.50}{9 h}}[/latex]
Dividing the first term by the second term to obtain the unit rate,
= $27.50/h
Therefore, his hourly rate of pay is $27.50 per hour, or $27.50/h.
Example 5.1-g: Using Unit Rates to Solve a World Problem
A car travels 90 km in 1.5 hours. At this rate, how many kilometres will it travel in 5 hours?
Solution
This question can be solved by first determining the unit rate.
The rate of speed is 90 kilometres in 1.5 hours.
Therefore, the number of km travelled per hour [latex]\displaystyle{= \frac{90 km}{1.5 h}}[/latex]
= 60 km/h
That is, the distance travelled in 1 hour = 60 km.
Therefore, the distance travelled in 5 hours = 60 × 5 = 300 km.
Example 5.1-h: Comparing Unit Rates
Car A requires 8.9 litres of gas to travel 100 km. Car B requires 45 litres of gas to travel 475 km. Which car has the better fuel economy?
Solution
Car A : 100 km requires 8.9 litres of gas.
Therefore, the number of km travelled per litre [latex]\displaystyle{= \frac{100 km}{8.9 L}}[/latex]
= 11.235955... = 11.24 km/L of gas
Car B : 475 km requires 45 litres of gas.
Therefore, the number of km travelled per litre [latex]\displaystyle{= \frac{475 km}{45 L}}[/latex]
= 10.555555... = 10.56 km/L of gas
Therefore, Car A has the better fuel economy.
Unit Price
Unit price is the unit rate that expresses the cost of an item (in dollars, cents, etc.) per one unit of that item. The price is always the numerator and the unit quantity is the denominator. That is, price is expressed per quantity of 1.
Examples of unit price are:
- Price of gas is $1.36 per litre ($1.36/L)
- Price of grapes is $2 per kilogram ($2/kg)
- Price of juice is $0.75 per can
If the total price for a given quantity of an item is known, to determine its unit price, divide the total price of the item by its quantity.
Unit price is used in comparing and making decisions in purchasing items when various options are available. We save money when we compare the unit prices of the same item in different sized containers or different packages to determine the cheaper price per unit for our purchases.
Example 5.1-i: Calculating the Unit Price of an Item
If 4 litres of milk cost $4.80, then what is the unit price of milk?
Solution
To determine the unit price of milk, divide the total price by the given quantity.
That is, divide $4.80 by 4 litres.
Unit price [latex]\displaystyle{= \frac{\$4.80}{4 L}}[/latex] = $1.20/L
Therefore, the unit price of milk is $1.20 per litre ($1.20/L).
Example 5.1-j: Comparing Unit Prices
5 kg of almonds cost $43.50 and 4 kg of almonds cost $34.20. Which is cheaper to buy based on its unit price?
Solution
5 kg of almonds cost $43.50
Therefore, unit price [latex]\displaystyle{= \frac{\$43.50}{5 kg}}[/latex] = $8.70/kg
4 kg of almonds cost $34.20
Therefore, unit price [latex]\displaystyle{= \frac{\$34.20}{4 kg}}[/latex] = $8.55/kg
Therefore, based on unit price, buying 4 kg of almonds for $34.20 is cheaper than buying 5 kg of almonds for $43.50.
Note: Unit rate and unit price problems can also be solved using the method of proportions as demonstrated in the next section.
Sharing Quantities Using Ratios
Sharing quantities refers to the allocation or distribution of a quantity into two or more portions (or units) based on a given ratio.
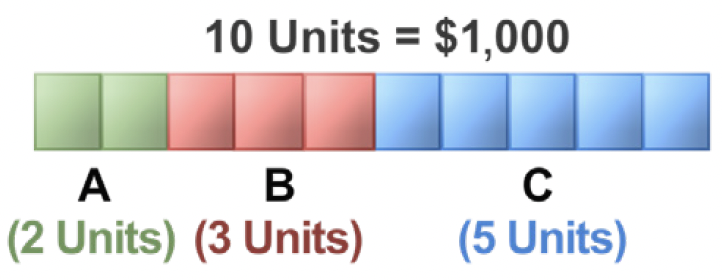
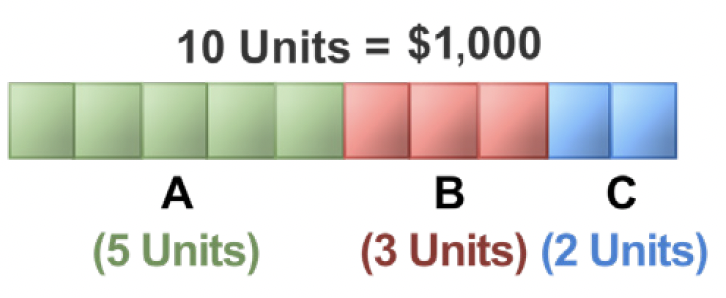
For example, to allocate last year's $1,000 profit among persons A, B, and C in the ratio of 2 : 3 : 5, first add the terms of the ratio (i.e., 2, 3, and 5), which results in a total of 10 units. These 10 units represent the total profit of $1,000, where A's share constitutes 2 units, B's 3 units, and C's 5 units, as shown in the diagram below.
Each person's share can then be calculated, as follows:
A's share [latex]\displaystyle{\frac{2}{10} \times 1,000.00 = \$200.00}[/latex]
B's share [latex]\displaystyle{\frac{3}{10} \times 1,000.00 = \$300.00}[/latex]
C's share [latex]\displaystyle{\frac{5}{10} \times 1,000.00 = \$500.00}[/latex]
- The total of A, B, and C's shares is equal to the profit amount of $1,000. That is, the shares of A + B + C = 200 + 300 + 500 = 1,000.
- If we reduce the ratio of the amounts shared by A, B, and C to its lowest terms, the result would be the original ratio. That is, 200 : 300 : 500 reduced to lowest terms is 2 : 3 : 5.
If this year, the ratio of A's share : B's share : C's share is changed to 5 : 3 : 2 (instead of last year's 2 : 3 : 5), and the profit of $1,000 remained the same, then their individual shares will change.
Their shares are recalculated as follows:
A's share [latex]\displaystyle{\frac{5}{10} \times 1,000.00 = \$500.00}[/latex]
B's share [latex]\displaystyle{\frac{3}{10} \times 1,000.00 = \$300.00}[/latex]
C's share [latex]\displaystyle{\frac{2}{10} \times 1,000.00 = \$200.00}[/latex]
- The total of A, B, and C's shares this year is still equal to the profit amount of $1,000. That is, the shares of A + B + C = 500 + 300 + 200 = 1,000.
- If we reduce the ratio of the amounts shared by A, B, and C to its lowest terms, the result would be the original ratio. That is, 500 : 300 : 200 reduced to lowest terms is 5 : 3 : 2.
Example 5.1-k: Sharing Quantities Using Ratios
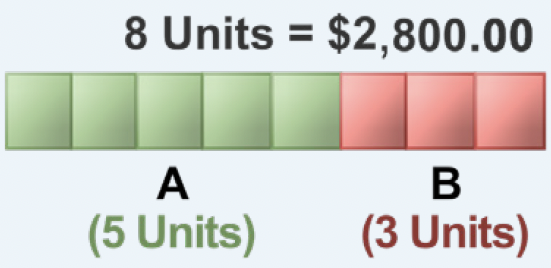
A, B, and C start a business and invest $3,500, $2,100, and $2,800, respectively. After a few months, C decides to sell his share of the business to A and B. How much would A and B have to pay for C's shares if A and B want to maintain their initial investment ratio?
Solution
The investments of A, B, and C are in the ratio of 3,500 : 2,100 : 2,800, which can be reduced to 5 : 3 : 4.
If A and B want to maintain their initial investment ratio of 5 : 3, then C's share (of $2,800) has to be paid for by A and B in the same ratio, 5 : 3.
By adding the terms of A and B, we know that C's share is to be divided into a total of 8 units, as illustrated:
A would have to pay C : [latex]\displaystyle{\frac{5}{8} \times 2,800.00 = \$1,750.00}[/latex]
B would have to pay C : [latex]\displaystyle{\frac{3}{8} \times 2,800.00 = \$1,050.00}[/latex]
Therefore, A would have to pay C $1,750 and B would have to pay C $1,050 in order to maintain their initial investment ratio.
Example 5.1-l: Sharing Quantities Using Fractional Ratios
The sum of all three angles of a triangle is 180 degrees. If the three angles of a triangle are in the ratio of [latex]\displaystyle{\frac{1}{6} : \frac{1}{3} : \frac{1}{4}}[/latex], calculate each angle of the triangle.
Solution
First, convert all the terms in the ratio to integers.
[latex]\displaystyle{\frac{1}{6} : \frac{1}{3} : \frac{1}{4}}[/latex]
Multiplying each term by the least common denominator 12,
2 : 4 : 3
This ratio is in lowest terms.
By adding all the terms, we know that the 180 degrees is to be divided into a total of 2 + 4 + 3 = 9 units.
1st angle: [latex]\displaystyle{\frac{2}{9} \times 180^\circ = 40^\circ}[/latex]
2nd angle: [latex]\displaystyle{\frac{4}{9} \times 180^\circ = 80^\circ}[/latex]
3rd angle: [latex]\displaystyle{\frac{3}{9} \times 180^\circ = 60^\circ}[/latex]
Therefore, the three angles of the triangle are 40°, 80°, and 60°, which sum to 40° + 80° + 60° = 180°.
Example 5.1-m: Application Using Equivalent Ratios
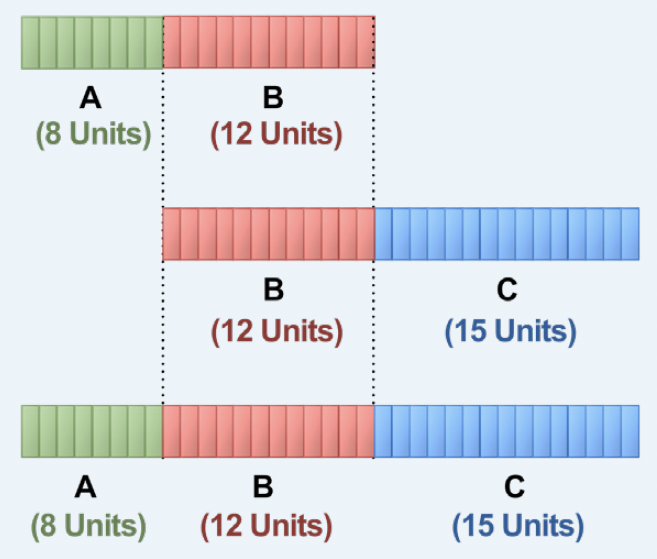
A fashion boutique is split into three departments: Clothing, Beauty products, and Accessories. Each department takes up a different area in the boutique. The ratio of the areas of Accessories to Beauty is 2 : 3, and that of Beauty to Clothing is 4 : 5. What is the ratio of the department areas of Accessories : Beauty : Clothing?
Solution
A : B = 2 : 3 and B : C = 4 : 5
Determine the equivalent ratios for A : B and B : C such that the number of units in B is the same in both ratios.
A : B = 2 : 3
Multiplying each term by 4,
= 8 : 12
B : C = 4 : 5
Multiplying each term by 3,
= 12 : 15
Therefore, the ratio of the department areas of Accessories : Beauty : Clothing in the boutique is 8 : 12 : 15.
5.1 Exercises
Answers to the odd-numbered questions are available at the end of the book.
For problems 1 and 2, determine whether the given pairs of ratios are equivalent.
- a. 4 : 6 and 6 : 10
b. 8 : 10 and 28 : 35
c. 6 : 8 and 27 : 32
d. 16 : 22 and 64 : 88
- a. 16 : 20 and 24 : 30
b. 10 : 12 and 35 : 42
c. 12 : 14 and 30 : 42
d. 12 : 26 and 30 : 65
Determine if the following ratios are equivalent or not equivalent to the ratio 6 : 9 : 12.
- a. 4 : 6 : 8
b. 2 : 3 : 4
c. 1 : 3 : 2
d. 8 : 12 : 16
Determine if the following ratios are equivalent or not equivalent to the ratio 6 : 9 : 12.
- a. 20 : 30 : 15
b. 8 : 12 : 6
c. 28 : 42 : 21
d. 24 : 36 : 18
For problems 5 to 8, express the ratios as (i) equivalent ratios in their lowest terms (as whole numbers), and (ii) equivalent ratios where the smallest term is 1.
- a. 18 : 48 : 30
b. 175 : 50 : 125
c. 0.45 : 1 : 2
- a. 27 : 45 : 72
b. 180 : 60 : 150
c. 2.4 : 0.75
- a. [latex]\displaystyle{\frac{2}{3} : \frac{1}{5}}[/latex]
b. [latex]\displaystyle{12 : \frac{5}{3} : 3}[/latex]
c. [latex]\displaystyle{1.7 : 8.5 : \frac{34}{3}}[/latex]
- a. [latex]\displaystyle{\frac{3}{2} : \frac{2}{5}}[/latex]
b. [latex]\displaystyle{65 : 91 : \frac{13}{2}}[/latex]
c. [latex]\displaystyle{12 : 1.5 : \frac{3}{2}}[/latex]
For problems 9 and 10, express the ratios in lowest terms.
- a. 9 months to 2 years
b. 750 g to 3 kg
c. 30 minutes to 1 hour and 15 minutes
- a. 3 weeks to 126 days
b. 120 g to 2 kg
c. 55 minutes to 2 hours and 45 minutes
- Emily was planning to make an authentic Indian dish for her guests. She planned to use 36 eggs, 6 litres of water, 3 tablespoons of chilli powder, and 12 tomatoes.
- What is the ratio of the ingredients in her recipe, expressed in lowest terms?
- If she decides to reduce the quantity of chilli powder to [latex]\displaystyle{1\frac{1}{2}}[/latex] tablespoons, calculate the new ratio of the ingredients in her recipe, expressed in lowest terms.
- In Murphy's battery manufacturing company, 600 kg of lead, 45 kg of carbon, 30 litres of battery acid, and 120 kg of rubber are used per day to make batteries.
- What is the ratio of the raw materials used per day to make batteries, expressed in lowest terms?
- If they alter the quantity of carbon used in the batteries and utilize 30 kg of carbon per day, calculate the new ratio of raw materials used per day, expressed in lowest terms.
For problems 13 to 20, determine the unit rate.
- 525 kilometres in 7 hours = ? km/h
- 680 kilometres in 8 hours = ? km/h
- 154 kilometres to 14 litres = ? km/L
- 228 kilometres to 19 litres = ? km/L
- 450 words typed in 6 minutes = ? words/min
- 496 words typed in 8 minutes = ? words/min
- 261 pages in 9 minutes = ? pages/min
- 192 pages in 8 minutes = ? pages/min
For problems 21 to 26, identify the option with the lower cost, based on unit price.
- 2 kg of flour for $3.30, or 5 kg of flour for $8.40.
- 3 kg of sugar for $3.90, or 5 kg of sugar for $6.25.
- 12 pencils for $4.44, or 8 pencils for $2.88.
- 6 litres of paint for $45.60, or 5 litres of paint for $37.25.
- 1.2 litres of juice for $2.16, or 0.8 litres of juice for $1.40.
- 2.2 kg of jam for $11.00, or 1.5 kg of jam for $7.20.
- In a race, participants are required to swim 3,850 metres and bike 7 kilometres. Calculate the ratio of the distance covered by swimming to the distance covered by biking, in its lowest terms.
- Adam, a hardware engineer, wants to install a microchip that is 38.2 mm in length into his laptop. The length of the installation space provided in his laptop is 4.8 cm. Calculate the ratio of the length of the microchip to the installation space, in its lowest terms.
- An aircraft travels a distance of 3,105 km in 5 hours and 45 minutes. Calculate the ratio of the distance traveled to the time taken, reduced to a rate of kilometres per hour.
- Speed is defined as the ratio of the distance travelled to the time taken. If Mary, who lives in Toronto, took 6 hours and 15 minutes to reach her parent's home in Montreal, which is 575 km away, calculate the average speed at which she was travelling in kilometres per hour.
- If A earns $196 for working 8 hours and B earns $98 for working 5 hours, whose hourly rate is higher?
- If Amanda travelled 325 km in 4 hours and 15 minutes and Ashton travelled 290 km in 3 hours and 30 minutes, whose average speed was greater?
- Kate earned $210 for 7.5 hours of work and Susan earned $249.75 for 9 hours of work.
a. Calculate their hourly rates.
b. Whose hourly rate was higher and by how much? - Jack's monthly pay is $4,200. Steve's weekly pay is $975.
a. Calculate their annual salaries. (1 year = 12 months = 52 weeks)
b. Whose annual salary is more and by how much? - A TV cable bill of $90 is shared between two housemates, Mike and Sarah, in the ratio of [latex]\displaystyle{2 : 2\frac{1}{2}}[/latex]. How much did each person pay?
- Alexander and Alyssa invested a total of $10,000 in a web-design business. If the ratio of their investments is 3 : 5, what were their investments?
- Amy and two of her friends received the first prize for a marketing case competition. They received an amount of $7,500; however, they decided to share the prize in the ratio of the amount of time each of them spent on the marketing case. If Amy spent 5 hours, Gary spent 8 hours, and Andrew spent 2 hours, what would be each person's share of the prize?
- Three friends, Andy, Berry, and Cassandra, jointly insured a commercial property in the ratio of 10 : 9 : 6, respectively. How will an annual premium of $8,000 be distributed among the three of them?
- The lengths of the three sides of a triangle are in the ratio of [latex]\displaystyle{\frac{3}{4} : \frac{2}{5} : \frac{1}{2}}[/latex]. If the perimeter of the triangle (i.e., the sum of the three sides lengths) is 66 cm, calculate the length of each side.
- The lengths of the three sides of a triangle are in the ratio of [latex]\displaystyle{\frac{2}{3} : \frac{5}{6} : \frac{4}{5}}[/latex]. If the perimeter of the triangle (i.e., the sum of the three sides lengths) is 128 cm, calculate the length of each side.
- Three friends, Alex, Brooks, and Charlie, have decided to invest $4,000, $6,000, and $2,000, respectively, to start a software development business. If Charlie decided to leave the business, how much would Alex and Brooks have to pay for Charlie's share if they want to maintain their initial investment ratio?
- Chuck decided to build a yacht with his two friends Rob and Bob; they invested $9,000, $11,000, and $6,500, respectively. After the yacht was built, Bob decided to sell his share of the investment to Chuck and Rob. How much would each of them have to pay if they want to maintain the same ratio of their investments in the yacht?
- A box contains red, green, and blue marbles. [latex]\displaystyle{\frac{1}{3}}[/latex] of the marbles are red, [latex]\displaystyle{\frac{2}{5}}[/latex] of the marbles are green, and the remaining marbles are blue.
- What fraction of the marbles in the box are blue?
- Calculate the ratio of red to green to blue (R : G : B) marbles in the box, expressed in its lowest terms (as whole numbers).
- If there are 75 marbles in the box, how many of each colour are there?
- A box contains black, white, and yellow marbles. [latex]\displaystyle{\frac{1}{4}}[/latex] of the marbles are black, [latex]\displaystyle{\frac{1}{3}}[/latex] of the marbles are white, and the remaining marbles are yellow.
- What fraction of the marbles in the box are yellow?
- Calculate the ratio of black to white to yellow (B : W : Y) marbles in the box, expressed in its lowest terms (as whole numbers).
- If there are 72 marbles in the box, how many of each colour are there?
- Abey and Baxter invested equal amounts of money in a business. A year later, Abey withdrew $7,500, making the ratio of their investments 5 : 9. How much money did each of them invest in the beginning?
- Jessica and Russel invested equal amounts to start a business. Two months later, Jessica invested an additional $3,000 in the business, making the ratio of their investments 11 : 5. How much money did each of them invest in the beginning?
- If A : B = 4 : 3 and B : C = 6 : 5, determine A : B : C.
- If X : Y = 5 : 2 and Y : Z = 7 : 6, determine X : Y : Z.
Unless otherwise indicated, this chapter is an adaptation of the eTextbook Foundations of Mathematics (3rd ed.) by Thambyrajah Kugathasan, published by Vretta-Lyryx Inc., with permission. Adaptations include supplementing existing material and reordering chapters.