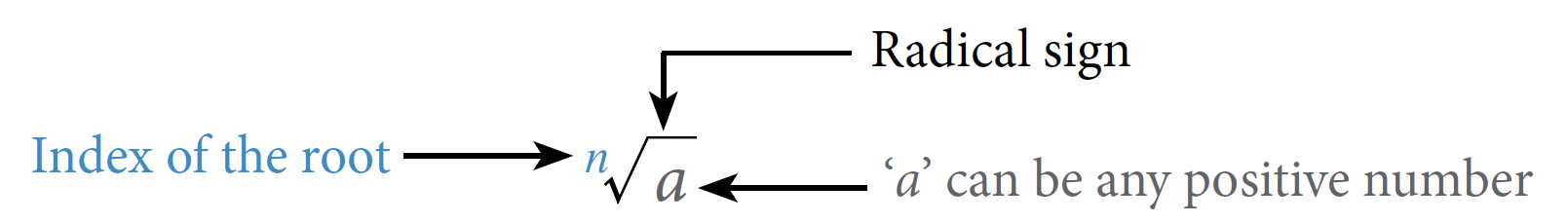3.2 Roots, Fractional Exponents, and Negative Exponents
Roots
Roots are the inverse operation of exponents.
In the previous chapters, we learned that taking the square root of a number is the inverse of raising a number to the power of 2.
For example,
- The square of 2 is [latex]2^2 = 4[/latex]. Therefore, the square root of 4 is [latex]\sqrt{4} = 2[/latex].
- The square of 3 is [latex]3^2 = 9[/latex]. Therefore, the square root of 9 is [latex]\sqrt{9} = 3[/latex].
We can also use roots to express the inverse of raising a number to a power greater than 2.
We know that,
[latex]9 = 3 \times 3 = 3^2[/latex]
Therefore, the square root (2nd root) of 9 is 3.
Similarly,
[latex]125 = 5 \times 5 \times 5 = 5^3[/latex]
Therefore, the cube root (3rd root) of 125 is 5.
[latex]16 = 2 \times 2 \times 2 \times2 = 2^4[/latex]
Therefore, the 4th root of 16 is 2.
The following notation is used to represent roots, also known as radicals
The index is written as a small number to the left of the radical sign. It indicates which root is to be taken.
For example,
- [latex]\sqrt[3]{125}[/latex] indicates the cube root (3rd root) of 125.
- [latex]\sqrt[4]{16}[/latex] indicates the 4th root of 16.
Note: Recall that for square roots, the index 2 does not need to be written as it is understood to be
there; i.e., [latex]\sqrt[2]{9} = \sqrt{9}[/latex].
Perfect Roots
Roots of a whole number may not be a whole number. A whole number is a perfect root if its root is also a whole number.
For example,
- 4 is a perfect square root of 16 because [latex]4^2 = 16[/latex]; i.e., [latex]\sqrt{16} = 4[/latex]
- 3 is a perfect cube root of 27 because [latex]3^3 = 27[/latex]; i.e., [latex]\sqrt[3]{27} = 3[/latex]
Table 3.2-a: Examples of Perfect Roots
| Roots | Square Roots | Cube Roots | Fourth Roots |
|---|---|---|---|
| [latex]1[/latex] | [latex]\sqrt{1}[/latex] | [latex]\sqrt[3]{1}[/latex] | [latex]\sqrt[4]{1}[/latex] |
| [latex]2[/latex] | [latex]\sqrt{4}[/latex] | [latex]\sqrt[3]{8}[/latex] | [latex]\sqrt[4]{16}[/latex] |
| [latex]3[/latex] | [latex]\sqrt{9}[/latex] | [latex]\sqrt[3]{27}[/latex] | [latex]\sqrt[4]{81}[/latex] |
| [latex]4[/latex] | [latex]\sqrt{16}[/latex] | [latex]\sqrt[3]{64}[/latex] | [latex]\sqrt[4]{256}[/latex] |
| [latex]5[/latex] | [latex]\sqrt{25}[/latex] | [latex]\sqrt[3]{125}[/latex] | [latex]\sqrt[4]{625}[/latex] |
| [latex]6[/latex] | [latex]\sqrt{36}[/latex] | [latex]\sqrt[3]{216}[/latex] | [latex]\sqrt[4]{1,296}[/latex] |
| [latex]7[/latex] | [latex]\sqrt{49}[/latex] | [latex]\sqrt[3]{343}[/latex] | [latex]\sqrt[4]{2,401}[/latex] |
| [latex]8[/latex] | [latex]\sqrt{64}[/latex] | [latex]\sqrt[3]{512}[/latex] | [latex]\sqrt[4]{4,096}[/latex] |
| [latex]9[/latex] | [latex]\sqrt{81}[/latex] | [latex]\sqrt[3]{729}[/latex] | [latex]\sqrt[4]{6,561}[/latex] |
| [latex]10[/latex] | [latex]\sqrt{100}[/latex] | [latex]\sqrt[3]{1,000}[/latex] | [latex]\sqrt[4]{10,000}[/latex] |
Simplifying Roots Using Perfect Roots
Just like we can simplify a power of a product, we can simplify a root of a product as follows:
[latex]\sqrt[n]{ab} = \sqrt[n]{a} \times \sqrt[n]{b}[/latex]
For example, [latex]\sqrt{10} = \sqrt{2 \times 5} = \sqrt{2} \times \sqrt{5}[/latex].
We can use this rule and our knowledge of perfect roots to simplify square and cube roots.
For example,
- To simplify [latex]\sqrt{12}[/latex], we can write 12 as the product [latex]4 \times 3[/latex], where one of the factors, 4, is a perfect square. Therefore,[latex]\sqrt{12} = \sqrt{4 \times 3} = \sqrt{4} \times \sqrt{3} = 2\sqrt{3}[/latex]
- To simplify [latex]\sqrt[3]{54}[/latex], we can write 54 as the product [latex]27 \times 2[/latex], where one of the factors, 27, is a perfect cube. Therefore,[latex]\sqrt[3]{54} = \sqrt[3]{27 \times 2} = \sqrt[3]{27} \times \sqrt[3]{2} = 3\sqrt[3]{2}[/latex]
Example 3.2-a: Simplifying Using Perfect Roots
Simplify using perfect roots of a number:
- [latex]\sqrt{72}[/latex]
- [latex]\sqrt[3]{40}[/latex]
Solution
- [latex]\sqrt{72} = \sqrt{36 \times 2} = \sqrt{36} \times \sqrt{2} = 6\sqrt{2}[/latex]
- [latex]\sqrt[3]{40} = \sqrt[3]{8 \times 5} = \sqrt[3]{8} \times \sqrt[3]{5} = 2\sqrt[3]{5}[/latex]
Fractional Exponents
A radical can also be represented using fractional exponents. Fractional exponents are often easier to write and perform operations with than radicals.
For example,
- The square (2nd) root of a number can be written as the number raised to the power of [latex]\displaystyle{\frac{1}{2}}[/latex].e.g., [latex]\displaystyle{\sqrt{5} = 5^{\frac{1}{2}}}[/latex]
- The cube (3rd) root of a number can be written as the number raised to the power of [latex]\displaystyle{\frac{1}{3}}[/latex].e.g., [latex]\displaystyle{\sqrt[3]{8} = 8^{\frac{1}{3}}}[/latex]
- The fourth (4th) root of a number can be written as the number raised to the power of [latex]\displaystyle{\frac{1}{4}}[/latex].e.g., [latex]\displaystyle{\sqrt[4]{5^3} = (5^3)^{\frac{1}{4}} = 5^{3 \times \frac{1}{4}} = 5^{\frac{3}{4}}}[/latex]
An appropriate radical will “undo” an exponent.
For example,
- [latex]\displaystyle{\sqrt{5^2} = (5^2)^{\frac{1}{2}} = 5^{2 \times \frac{1}{2}} = 5}[/latex]
- [latex]\displaystyle{\sqrt[3]{7^3} = (7^3)^{\frac{1}{3}} = 7^{3 \times \frac{1}{3}} = 7}[/latex]
Example 3.2-b: Expressions in Radical Form
Express the following in radical form:
- [latex]\displaystyle{2^{\frac{5}{6}}}[/latex]
- [latex]\displaystyle{3^{\frac{2}{5}}}[/latex]
- [latex]\displaystyle{\left(\frac{2}{3}\right)^{\frac{3}{4}}}[/latex]
Solution
- [latex]\displaystyle{2^{\frac{5}{6}} = \sqrt[6]{2^5}}[/latex]
- [latex]\displaystyle{3^{\frac{2}{5}} = \sqrt[5]{3^2}}[/latex]
- [latex]\displaystyle{\left(\frac{2}{3}\right)^{\frac{3}{4}} = \sqrt[4]{\left(\frac{2}{3}\right)}}[/latex]
Evaluating Expressions with Fractional Exponents Using a Calculator
When entering a fractional exponent in a calculator, brackets must be used.
For example, to evaluate [latex]\displaystyle{25^{\frac{2}{5}}}[/latex] using a calculator, enter it as follows:
Note: Without the brackets, the operation will mean [latex](25)^2 \div 5[/latex], which is incorrect.
Example 3.2-c: Evaluating Expressions with Fractional Exponents Using a Calculator
Evaluate the following using a calculator:
- [latex]\displaystyle{15^{\frac{3}{2}}}[/latex]
- [latex]\displaystyle{\left(\frac{3}{5}\right)^{\frac{1}{4}}}[/latex]
- [latex]\displaystyle{(2.5)^{\frac{3}{7}}}[/latex]
Solution
Arithmetic Operations with Fractional Exponents
All the rules of exponents, Product Rule, Quotient Rule, Power of a Product Rule, Power of a Quotient Rule, Power of a Power Rule, etc., learned in Section 3.1 and as outlined in Tables 3.1-a and 3.1-b are applicable to fractional exponents.
Example 3.2-d: Evaluating Expressions with Fractional Exponents using the Product Rule
Simplify the following using the Product Rule to express as a single power, and then evaluate to two decimal places, where applicable.
- [latex]\displaystyle{2^{\frac{1}{2}} \times 2^{\frac{1}{3}}}[/latex]
- [latex]\displaystyle{3^{\frac{3}{4}} \times 3^{\frac{9}{4}} \times 3^0}[/latex]
- [latex]\displaystyle{\left(\frac{3}{5}\right)^{\frac{7}{3}} \times \left(\frac{3}{5}\right)^{\frac{2}{3}}}[/latex]
Solution
- [latex]\displaystyle{2^{\frac{1}{2}} \times 2^{\frac{1}{3}} = 2^{\left(\frac{1}{2} + \frac{1}{3}\right)} = 2^{\left(\frac{3 + 2}{6}\right)} = 2^{\frac{5}{6}} = 1.781797... = 1.78}[/latex]
- [latex]\displaystyle{3^{\frac{3}{4}} \times 3^{\frac{9}{4}} \times 3^0 = 3^{\left(\frac{3}{4} + \frac{9}{4} + 0\right)} = 3^{\frac{12}{4}} = 3^3 = 27}[/latex]
- [latex]\displaystyle{\left(\frac{3}{5}\right)^{\frac{7}{3}} \times \left(\frac{3}{5}\right)^{\frac{2}{3}} = \left(\frac{3}{5}\right)^{\left(\frac{7}{3} + \frac{2}{3}\right)} = \left(\frac{3}{5}\right)^{\frac{9}{3}} = \left(\frac{3}{5}\right)^3 = 0.216 = 0.22}[/latex]
Example 3.2-e: Evaluating Expressions with Fractional Exponents using the Quotient Rule
Simplify the following using the Quotient Rule to express as a single power, and then evaluate to two decimal places, where applicable.
- [latex]\displaystyle{2^{\frac{4}{3}} \div 2^{\frac{2}{3}}}[/latex]
- [latex]\displaystyle{(1.2)^{\frac{5}{2}} \div (1.2)^{\frac{1}{2}}}[/latex]
- [latex]\displaystyle{\left(\frac{1}{3}\right)^{\frac{6}{4}} \div \left(\frac{1}{3}\right)^{\frac{3}{4}}}[/latex]
Solution
- [latex]\displaystyle{2^{\frac{4}{3}} \div 2^{\frac{2}{3}} = 2^{\left(\frac{4}{3} - \frac{2}{3}\right)} = 2^{\frac{2}{3}} = 1.587401... = 1.59}[/latex]
- [latex]\displaystyle{(1.2)^{\frac{5}{2}} \div (1.2)^{\frac{1}{2}} = (1.2)^{\left(\frac{5}{2} - \frac{1}{2}\right)} = (1.2)^{\frac{4}{2}} = (1.2)^2 = 1.44}[/latex]
- [latex]\displaystyle{\left(\frac{1}{3}\right)^{\frac{6}{4}} \div \left(\frac{1}{3}\right)^{\frac{3}{4}} = \left(\frac{1}{3}\right)^{\left(\frac{6}{4} - \frac{3}{4}\right)} = \left(\frac{1}{3}\right)^{\frac{3}{4}} = 0.438691... = 0.44}[/latex]
Example 3.2-f: Evaluating Expressions with Fractional Exponents using the Power of a Product Rule
Simplify the following using the Power of a Product Rule, and then evaluate to two decimal places, where applicable.
- [latex]\displaystyle{(4^2 \times 3^2)^{\frac{1}{2}}}[/latex]
- [latex]\displaystyle{\left(7^2 \times \frac{1}{3^2}\right)^{\frac{1}{2}}}[/latex]
- [latex]\displaystyle{(2^6 \times 3^2)^{\frac{3}{2}}}[/latex]
Solution
- [latex]\displaystyle{(4^2 \times 3^2)^{\frac{1}{2}} = (4^2)^{\frac{1}{2}} \times (3^2)^{\frac{1}{2}} = 4 \times 3 = 12}[/latex]
- [latex]\displaystyle{\left(7^2 \times \frac{1}{3^2}\right)^{\frac{1}{2}} = (7^2)^{\frac{1}{2}} \times \left(\frac{1}{3^2}\right)^{\frac{1}{2}} = \frac{7}{3} = 2.333333... = 2.33}[/latex]
- [latex]\displaystyle{(2^6 \times 3^2)^{\frac{3}{2}} = (2^6)^{\frac{3}{2}} \times (3^2)^{\frac{3}{2}} = 2^{\left(6 \times \frac{3}{2}\right)} \times 3^{\left(2 \times \frac{3}{2}\right)} = 2^9 \times 3^3 = 512 \times 27 = 13,824}[/latex]
Example 3.2-g: Evaluating Expressions with Fractional Exponents using the Power of a Quotient Rule
Simplify the following using the Power of a Quotient Rule, and then evaluate to two decimal places, where applicable.
- [latex]\displaystyle{\left(\frac{4^2}{3^2}\right)^{\frac{1}{2}}}[/latex]
- [latex]\displaystyle{\left(\frac{5^3}{2^6}\right)^{\frac{1}{3}}}[/latex]
Solution
- [latex]\displaystyle{\left(\frac{4^2}{3^2}\right)^{\frac{1}{2}} = \frac{(4^2)^{\frac{1}{2}}}{(3^2)^{\frac{1}{2}}} = \frac{4}{3} = 1.333333... = 1.33}[/latex]
- [latex]\displaystyle{\left(\frac{5^3}{2^6}\right)^{\frac{1}{3}} = \frac{(5^3)^{\frac{1}{3}}}{(2^6)^{\frac{1}{3}}} = \frac{5}{2^{\frac{6}{3}}} = \frac{5}{2^2} = \frac{5}{4} = 1.25}[/latex]
Example 3.2-h: Evaluating Expressions with Fractional Exponents using the Power of a Power Rule
Simplify the following using the Power of a Power Rule to express as a single power, and then evaluate to two decimal places, where applicable.
- [latex]\displaystyle{\left(6^{\frac{1}{2}}\right)^3}[/latex]
- [latex]\displaystyle{\left(18^{\frac{1}{3}}\right)^{\frac{1}{4}}}[/latex]
- [latex]\displaystyle{\left[\left(\frac{2}{3}\right)^3\right]^2}[/latex]
Solution
- [latex]\displaystyle{\left(6^{\frac{1}{2}}\right)^3 = 6^{\left(\frac{1}{2} \times 3\right)} = 6^{\frac{3}{2}} = 14.696938... = 14.70}[/latex]
- [latex]\displaystyle{\left(18^{\frac{1}{3}}\right)^{\frac{1}{4}} = 18^{\left(\frac{1}{3} \times \frac{1}{4}\right)} = 18^{\frac{1}{12}} = 1.272348... = 1.27}[/latex]
- [latex]\displaystyle{\left[\left(\frac{2}{3}\right)^3\right]^2 = \left(\frac{2}{3}\right)^{3 \times 2} = \left(\frac{2}{3}\right)^6 = \frac{2^6}{3^6} = \frac{64}{729} = 0.087791... = 0.09}[/latex]
Example 3.2-i: Evaluating Expressions with Fractional Exponents and Different Bases
Evaluate the following to two decimal places, where applicable.
- [latex]\displaystyle{16^{\frac{1}{2}} + 8^{\frac{1}{2}}}[/latex]
- [latex]\displaystyle{25^{\frac{1}{2}} - 27^{\frac{1}{3}}}[/latex]
- [latex]\displaystyle{\left(\frac{7}{8}\right)^{\frac{1}{4}} - \left(\frac{2}{3}\right)^{\frac{1}{3}}}[/latex]
- [latex]\displaystyle{5^{\frac{1}{2}} \times 3^{\frac{1}{2}}}[/latex]
- [latex]\displaystyle{2^{\frac{3}{4}} \div 3^{\frac{1}{2}}}[/latex]
- [latex]\displaystyle{5^{2\frac{3}{4}}}[/latex]
Solution
- [latex]\displaystyle{16^{\frac{1}{2}} + 8^{\frac{1}{2}} = 4 + 2.828427... = 6.828427... = 6.83}[/latex]
- [latex]\displaystyle{25^{\frac{1}{2}} - 27^{\frac{1}{3}} = 5 - 3 = 2}[/latex]
- [latex]\displaystyle{\left(\frac{7}{8}\right)^{\frac{1}{4}} - \left(\frac{2}{3}\right)^{\frac{1}{3}} = 0.967168... - 0.873580... = 0.093587... = 0.09}[/latex]
- [latex]\displaystyle{5^{\frac{1}{2}} \times 3^{\frac{1}{2}} = 2.236067... \times 1.732050... = 3.872983... = 3.87}[/latex]
- [latex]\displaystyle{2^{\frac{3}{4}} \div 3^{\frac{1}{2}} = 1.681792... \div 1.732050... = 0.970983... = 0.97}[/latex]
- [latex]\displaystyle{5^{2\frac{3}{4}} = 5^{\frac{11}{4}} = 83.592538... = 83.59}[/latex]
Negative Exponents
In exponential notation, the base of the number may be raised to a negative exponent. We can represent this as [latex]\boldsymbol{a^{-n}}[/latex]. A power with a negative exponent is the reciprocal of the power with the positive exponent.
Positive Exponent:
[latex]\boldsymbol{a^n} = a \times a \times a \times … \times a[/latex]
(multiplication of [latex]'n'[/latex] factors of [latex]'a'[/latex])
Negative Exponent:
[latex]\displaystyle{\boldsymbol{a^{-n} = \frac{1}{a^n}} = \frac{1}{a \times a \times a \times … \times a}}[/latex]
(division of [latex]'n'[/latex] factors of [latex]'a'[/latex])

[latex]\displaystyle{a^{-n} = \frac{1}{a^n}}[/latex], and [latex]\displaystyle{\frac{1}{a^{-n}} = a^n}[/latex]
Therefore, [latex]a^n[/latex] and [latex]a^{-n}[/latex] are reciprocals.
Any positive base with a negative exponent will always result in a positive answer.
Table 3.2-b: Examples of Negative and Positive Exponential Notation
| Negative Exponential Notation |
Positive Exponential Notation |
Repeated Division |
Standard Notation |
|---|---|---|---|
| [latex]5^{-1}[/latex] | [latex]\displaystyle{\frac{1}{5^1}}[/latex] | [latex]\displaystyle{\frac{1}{5}}[/latex] | [latex]\displaystyle{\frac{1}{5}}[/latex] |
| [latex]5^{-2}[/latex] | [latex]\displaystyle{\frac{1}{5^2}}[/latex] | [latex]\displaystyle{\frac{1}{5 \times 5}}[/latex] | [latex]\displaystyle{\frac{1}{25}}[/latex] |
| [latex]5^{-3}[/latex] | [latex]\displaystyle{\frac{1}{5^3}}[/latex] | [latex]\displaystyle{\frac{1}{5 \times 5 \times 5}}[/latex] | [latex]\displaystyle{\frac{1}{125}}[/latex] |
The properties (rules) of exponents in Section 3.1 of this chapter (summarized in Table 3.1-a) also apply to all negative exponents. We can use these properties to simplify powers with negative exponents and then convert negative exponents to positive exponents.
Example 3.2-j: Multiplying and Dividing Powers with Negative Exponents
Simplify the following and express the answer in exponential form with positive exponents:
- [latex]2^{-2} \times 2^{-3}[/latex]
- [latex]\displaystyle{\frac{3^{-4}}{3^{-2}}}[/latex]
- [latex](3 \times 5)^{-2}[/latex]
- [latex](3^{-2})^3[/latex]
Solution
- [latex]\displaystyle{2^{-2} \times 2^{-3} = 2^{-2 + (-3)} = 2^{-2 - 3} = 2^{-5} = \frac{1}{2^5}}[/latex]
- [latex]\displaystyle{\frac{3^{-4}}{3^{-2}} = 3^{-4 - (-2)} = 3^{-4 + 2} = 3^{-2} = \frac{1}{3^2}}[/latex]
- [latex]\displaystyle{(3 \times 5)^{-2} = 3^{-2} \times 5^{-2} = \frac{1}{3^2} \times \frac{1}{5^2}}[/latex]
- [latex]\displaystyle{(3^{-2})^3 = 3^{-2(3)} = 3^{-6} = \frac{1}{3^6}}[/latex]
Fractions with Negative Exponents
When a fraction has a negative exponent, change the fraction to its reciprocal and drop the negative sign from the exponent. After this change, the exponent indicates the number of times the numerator and denominator should be multiplied.
[latex]\displaystyle{\boldsymbol{\left(\frac{a}{b}\right)^{-n} = \left(\frac{b}{a}\right)^n}}[/latex]
For example,
[latex]\displaystyle{\left(\frac{2}{5}\right)^{-3} = \left(\frac{5}{2}\right)^3 = \left(\frac{2}{5}\right)\left(\frac{2}{5}\right)\left(\frac{2}{5}\right) = \frac{5 \times 5 \times 5}{2 \times 2 \times 2} = \frac{125}{8}}[/latex]
Note: The reciprocal of [latex]\displaystyle{\frac{2}{5}}[/latex] is [latex]\displaystyle{\frac{5}{2}}[/latex].
Example 3.2-k: Evaluating Fractions with Negative Exponents
Evaluate the following to two decimal places, where applicable.
- [latex]\displaystyle{\left(\frac{5}{4}\right)^{-2} \times \left(\frac{2}{3}\right)^{-3}}[/latex]
- [latex]\displaystyle{\left(\frac{3}{5}\right)^{-3} \div \left(\frac{2}{5}\right)^{-2}}[/latex]
Solution
- [latex]\displaystyle{\left(\frac{5}{4}\right)^{-2} \times \left(\frac{2}{3}\right)^{-3} = \left(\frac{4}{5}\right)^2 \times \left(\frac{3}{2}\right)^3 = \frac{4^2}{5^2} \times \frac{3^3}{2^3}}[/latex][latex]\displaystyle{= \frac{16}{25} \times \frac{27}{8} = \frac{2}{25} \times \frac{27}{1} = \frac{54}{25} = 2\frac{4}{25} = 2.16}[/latex]
- [latex]\displaystyle{\left(\frac{3}{5}\right)^{-3} \div \left(\frac{2}{5}\right)^{-2} = \left(\frac{5}{3}\right)^3 \div \left(\frac{5}{2}\right)^2 = \frac{5^3}{3^3} \div \frac{5^2}{2^2}}[/latex][latex]\displaystyle{= \frac{125}{27} \div \frac{25}{4} = \frac{125}{27} \times \frac{4}{25} = \frac{5}{27} \times \frac{4}{1} = \frac{20}{27} = 0.740740... = 0.74}[/latex]
3.2 Exercises
Answers to the odd-numbered problems are available at the end of the textbook.
Express Problems 1 to 4 in their radical form and evaluate.
- a. [latex]\displaystyle{64^{\frac{1}{2}}}[/latex] b. [latex]\displaystyle{\left(\frac{25}{16}\right)^{\frac{1}{2}}}[/latex]
- a. [latex]\displaystyle{81^{\frac{1}{2}}}[/latex] b. [latex]\displaystyle{\left(\frac{8}{25}\right)^{\frac{1}{2}}}[/latex]
- a. [latex]\displaystyle{8^{\frac{1}{3}}}[/latex] b. [latex]\displaystyle{\left(\frac{27}{64}\right)^{\frac{1}{3}}}[/latex]
- a. [latex]\displaystyle{64^{\frac{1}{3}}}[/latex] b. [latex]\displaystyle{\left(\frac{125}{8}\right)^{\frac{1}{3}}}[/latex]
Express problems 5 to 10 in their fractional exponent form and then evaluate, round to two decimal places, wherever applicable.
- a. [latex]\sqrt{144}[/latex] b. [latex]\sqrt[3]{64}[/latex]
- a. [latex]\sqrt{81}[/latex] b. [latex]\sqrt[3]{125}[/latex]
- a. [latex]\sqrt{2^6}[/latex] b. [latex]\sqrt{40}[/latex]
- a. [latex]\sqrt{3^4}[/latex] b. [latex]\sqrt{50}[/latex]
- a. [latex]\sqrt{8} \times \sqrt{12}[/latex] b. [latex]\sqrt{7} \times \sqrt{14}[/latex]
- a. [latex]\sqrt{12} \times \sqrt{10}[/latex] b. [latex]\sqrt{9} \times \sqrt{27}[/latex]
Express problems 11 and 12 in their fractional exponent form and then evaluate. Express your answer as a simplified fraction.
- a. [latex]\displaystyle{\sqrt{\frac{25}{49}}}[/latex] b. [latex]\displaystyle{\sqrt{\frac{64}{9}}}[/latex]
- a. [latex]\displaystyle{\sqrt{\frac{36}{64}}}[/latex] b. [latex]\displaystyle{\sqrt{\frac{169}{16}}}[/latex]
Express problems 13 and 14 in their fractional exponent form with a single base, and then evaluate, round to two decimal places, wherever applicable.
- a. [latex]\sqrt[4]{2^2 \times 2}[/latex] b. [latex]\sqrt[4]{5^2 \times 25^2}[/latex]
- a. [latex]\sqrt{3^4 \times 3^2}[/latex] b. [latex]\sqrt[6]{9^3 \times 27^4}[/latex]
Simplify problems 15 to 24 by expressing the powers using a single exponent and then evaluate, round to two decimal places, wherever applicable.
- a. [latex]\displaystyle{5^{\frac{1}{2}} \times 5^{\frac{3}{4}}}[/latex] b. [latex]\displaystyle{3^{\frac{7}{8}} \times 3^{\frac{5}{9}}}[/latex]
- a. [latex]\displaystyle{3^{\frac{1}{2}} \times 3^{\frac{1}{4}}}[/latex] b. [latex]\displaystyle{11^{\frac{3}{4}} \times 11^{\frac{2}{3}}}[/latex]
- a. [latex]\displaystyle{8^{\frac{4}{5}} \times 8^{\frac{2}{5}} \times 8^{\frac{1}{5}}}[/latex] b. [latex]\displaystyle{5^{\frac{1}{3}} \times 5^{\frac{1}{2}} \times 5^0}[/latex]
- a. [latex]\displaystyle{5^{\frac{4}{7}} \times 5^{\frac{4}{7}} \times 5^{\frac{6}{7}}}[/latex] b. [latex]\displaystyle{9^{\frac{5}{8}} \times 9^{\frac{2}{3}} \times 9^0}[/latex]
- a. [latex]\displaystyle{8^{\frac{1}{3}} \times 8^{\frac{2}{3}} \times 8^1}[/latex] b. [latex]\displaystyle{\frac{3^{\frac{8}{3}}}{3^2}}[/latex]
- a. [latex]\displaystyle{2^{\frac{2}{3}} \times 2^{\frac{1}{2}} \times 2^1}[/latex] b. [latex]\displaystyle{\frac{6^{\frac{7}{2}}}{6^2}}[/latex]
- a. [latex]\displaystyle{\frac{4^{\frac{5}{7}}}{4^{\frac{2}{7}}}}[/latex] b. [latex]\displaystyle{(3^2)^{\frac{1}{3}}}[/latex]
- a. [latex]\displaystyle{\frac{2^{\frac{4}{5}}}{2^{\frac{3}{5}}}}[/latex] b. [latex](10^3)^0[/latex]
- a. [latex]\displaystyle{\left(12^{\frac{1}{2}}\right)^4}[/latex] b. [latex]\displaystyle{\left(7^{\frac{1}{4}}\right)^8}[/latex]
- a. [latex]\displaystyle{\left(5^{\frac{2}{3}}\right)^6}[/latex] b. [latex]\displaystyle{\left(4^{\frac{2}{3}}\right)^6}[/latex]
Evaluate problems 25 to 32, round to two decimal places, wherever applicable.
- a. [latex]\displaystyle{5^{\frac{1}{2}} + 7^{\frac{1}{2}}}[/latex] b. [latex]\displaystyle{16^{\frac{1}{2}} - 9^{\frac{1}{2}}}[/latex]
- a. [latex]\displaystyle{125^{\frac{1}{3}} + 64^{\frac{1}{3}}}[/latex] b. [latex]\displaystyle{50^{\frac{1}{2}} - 40^{\frac{1}{2}}}[/latex]
- a. [latex]\displaystyle{5 \times 3^{\frac{1}{2}} + 2^{\frac{1}{2}}}[/latex] b. [latex]\displaystyle{(2^5)^{\frac{1}{2}} - (5^2)^{\frac{1}{2}}}[/latex]
- a. [latex]\displaystyle{12 \times 10^{\frac{1}{2}} + 5^{\frac{1}{2}}}[/latex] b. [latex]\displaystyle{(3^4)^{\frac{1}{3}} - (4^3)^{\frac{1}{4}}}[/latex]
- a. [latex]\displaystyle{8^{\frac{1}{2}} \times 9^{\frac{1}{2}}}[/latex] b. [latex]\displaystyle{45^{\frac{1}{2}} \times 60^{\frac{1}{2}}}[/latex]
- a. [latex]\displaystyle{6^{\frac{1}{2}} \times 3^{\frac{1}{2}}}[/latex] b. [latex]\displaystyle{24^{\frac{1}{2}} \times 75^{\frac{1}{2}}}[/latex]
- a. [latex]\displaystyle{\frac{5 + 4^{\frac{1}{2}}}{36^{\frac{1}{2}}}}[/latex] b. [latex]\displaystyle{\frac{10^{\frac{1}{2}} - 5^{\frac{1}{2}}}{25^{\frac{1}{2}}}}[/latex]
- a. [latex]\displaystyle{\frac{6^{\frac{1}{2}} + 6^{\frac{1}{2}}}{9^{\frac{1}{2}}}}[/latex] b. [latex]\displaystyle{\frac{7 - 7^{\frac{1}{2}}}{4^{\frac{1}{2}}}}[/latex]
Simplify problems 33 to 42 by expressing the powers using a single exponent and as a radical (where applicable), and then evaluate. Round to two decimal places, wherever applicable.
- a. [latex]\displaystyle{6^{-\frac{5}{4}} \times 6^{\frac{3}{4}}}[/latex] b. [latex]\displaystyle{7^{\frac{4}{3}} \times 7^{-\frac{2}{3}}}[/latex]
- a. [latex]\displaystyle{5^{\frac{4}{9}} \times 5^{-\frac{2}{9}}}[/latex] b. [latex]\displaystyle{3^{-\frac{6}{7}} \times 3^{\frac{2}{7}}}[/latex]
- a. [latex]\displaystyle{\frac{10^{-\frac{3}{5}} \times 10^{\frac{4}{5}}}{10^{\frac{2}{5}}}}[/latex] b. [latex]\displaystyle{\frac{2^{\frac{5}{7}} \times 2^{-\frac{6}{7}}}{2^{-\frac{8}{7}}}}[/latex]
- a. [latex]\displaystyle{\frac{5^{\frac{2}{7}} \times 5^{\frac{4}{7}}}{5^{-\frac{6}{7}}}}[/latex] b. [latex]\displaystyle{\frac{3^{\frac{2}{3}} - 3^{-\frac{4}{3}}}{3^{\frac{5}{3}}}}[/latex]
- a. [latex]\displaystyle{\frac{6^{-\frac{5}{9}} \times 6^0}{6^{\frac{7}{9}}}}[/latex] b. [latex]\displaystyle{\frac{7^{\frac{7}{8}} \times 7^{\frac{8}{3}}}{7^2}}[/latex]
- a. [latex]\displaystyle{\frac{9^{\frac{2}{5}} \times 9^0}{9^{\frac{3}{5}}}}[/latex] b. [latex]\displaystyle{\frac{5^{\frac{5}{6}} \times 5^{\frac{2}{3}}}{5^2}}[/latex]
- a. [latex]\displaystyle{(5^{-2})^{\frac{4}{3}}}[/latex] b. [latex]\displaystyle{\left(6^{-\frac{1}{2}}\right)^{-6}}[/latex]
- a. [latex]\displaystyle{(4^{-2})^{\frac{5}{2}}}[/latex] b. [latex]\displaystyle{\left(2^{-\frac{4}{5}}\right)^{-5}}[/latex]
- a. [latex]\displaystyle{\left(8^{-\frac{2}{3}}\right)^{-6}}[/latex] b. [latex]\displaystyle{\left(7^{-\frac{1}{3}}\right)^9}[/latex]
- a. [latex]\displaystyle{\left(6^{-\frac{2}{3}}\right)^{-3}}[/latex] b. [latex]\displaystyle{\left(3^{-\frac{4}{9}}\right)^0}[/latex]
Evaluate problems 43 to 48, round to two decimal places, wherever applicable.
- a. [latex]\displaystyle{\frac{3^{-1}}{2^{-1}}}[/latex] b. [latex]3^{-1} + 2^{-1}[/latex]
- a. [latex]\displaystyle{\frac{2^{-2}}{3^{-1}}}[/latex] b. [latex]2^{-2} + 3^{-1}[/latex]
- a. [latex]3^{-1} \times 3^2 \times 3^{-2}[/latex] b. [latex][2^{-3}]^{-1}[/latex]
- a. [latex]5^{-2} \times 5^2 \times 5^3[/latex] b. [latex][5^{-2}]^{-2}[/latex]
- a. [latex]\displaystyle{\frac{2^{\frac{2}{5}} + 3^0 \times 2^{-1}}{\left(\frac{1}{2}\right)^{-1}}}[/latex] b. [latex]\displaystyle{2^{-2} + \frac{1}{2^{-1}}}[/latex]
- a. [latex]\displaystyle{\frac{3^{-1} + 2 \times 3^{-1}}{\left(\frac{1}{3}\right)^{-1}}}[/latex] b. [latex]\displaystyle{3^{-2} + \frac{1}{3^{-1}}}[/latex]
Unless otherwise indicated, this chapter is an adaptation of the eTextbook Foundations of Mathematics (3rd ed.) by Thambyrajah Kugathasan, published by Vretta-Lyryx Inc., with permission. Adaptations include supplementing existing material and reordering chapters.