3.1 Exponents and Properties (Rules) of Exponents
In Chapters 1 and 2, we learned about powers of whole numbers, fractions, and decimal numbers.
Recall that when a number is raised to a whole number exponent, we can think of it as repeated multiplication. Powers are a simpler way to indicate repeated multiplication, similar to how multiplication is a simpler way to indicate repeated addition. Powers are expressed using exponential notation.
For example, the whole number 2 multiplied by itself 5 times is written in exponential notation as:
base [latex]\longrightarrow2^{5\longleftarrow}[/latex] exponent
2 is the base, 5 is the exponent, and the whole representation [latex]2^5[/latex] is known as the power.
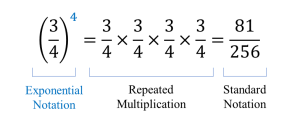
Similarly, the fraction [latex]\displaystyle{\frac{3}{4}}[/latex] multiplied by itself 4 times is written in exponential notation as:
base [latex]\longrightarrow\displaystyle{\left(\frac{3}{4}\right)}^{4\nwarrow}[/latex] exponent
[latex]\displaystyle{\frac{3}{4}}[/latex] is the base, 4 is the exponent, and the whole representation [latex]\displaystyle{\left(\frac{3}{4}\right)}^4[/latex] is the power.
Similarly, the decimal number 1.2 multiplied by itself 3 times is written in exponential notation as:
base [latex]\longrightarrow(1.2)^{3\longleftarrow}[/latex] exponent
1.2 is the base, 3 is the exponent, and the whole representation [latex](1.2)^3[/latex] is the power.
Properties (Rules) of Exponents
The following properties of exponents, known as the rules or laws of exponents, are used to simplify expressions that involve exponents.
Product of Powers (Product Rule)
To multiply powers with the same base, add their exponents.
For example,
[latex]7^5 \times 7^3 = (7 \times 7 \times 7 \times 7 \times 7) \times (7 \times 7 \times 7)[/latex]
[latex]= (7 \times 7 \times 7 \times 7 \times 7 \times 7 \times 7 \times 7)[/latex]
[latex]= 7^8[/latex], which is the same as [latex]= 7^{(5 + 3)}[/latex]
You will note that the resulting exponent, 8, can be obtained by adding the exponents 5 and 3 since the powers have the same base.
In general, for powers with base ‘a’ and exponents ‘m’ and ‘n’,
[latex]\boldsymbol{a^m \times a^n = a^{(m + n)}}[/latex]
Note: [latex]a^m + a^n \neq a^{(m + n)}[/latex]
Example 3.1-a: Simplifying Exponential Expressions Using the Product Rule
Express the following as a single power:
- [latex]2^3 \times 2^4 \times 2^2[/latex]
- [latex]\displaystyle{\left(\frac{3}{5}\right)^6 \times \left(\frac{3}{5}\right)^2}[/latex]
- [latex](0.2)^3 \times (0.2)^2[/latex]
Solution
- [latex]2^3 \times 2^4 \times 2^2 = 2^{(3 + 4 + 2)} = 2^9[/latex]
- [latex]\displaystyle{\left(\frac{3}{5}\right)^6 \times \left(\frac{3}{5}\right)^2 = \left(\frac{3}{5}\right)^{(6 + 2)} = \left(\frac{3}{5}\right)^8}[/latex]
- [latex](0.2)^3 \times (0.2)^2 = (0.2)^{3 + 2} = (0.2)^5[/latex]
Quotient of Powers (Quotient Rule)
To divide two powers with the same base, subtract their exponents.
For example,
[latex]4^7 \div 4^2 = \displaystyle{\frac{4 \times 4 \times 4 \times 4 \times 4 \times 4 \times 4}{4 \times 4}}[/latex]
[latex]= \displaystyle{\frac{4 \times 4}{4 \times 4} \times 4 \times 4 \times 4 \times 4 \times 4}[/latex]
[latex]= 1 \times 4 \times 4 \times 4 \times 4 \times 4[/latex]
[latex]= 4^5[/latex], which is the same as [latex]= 4^{(7 - 2)}[/latex]
You will note that the resulting exponent, 5, can be obtained by subtracting the denominator’s exponent from the numerator’s exponent (7 − 2 = 5) since the powers have the same base.
In general, for powers with a non-zero base ‘a’ and exponents ‘m’ and ‘n’,
[latex]\boldsymbol{\displaystyle{\frac{a^m}{a^n} = a^{(m - n)}}}[/latex], where [latex]\boldsymbol{a \neq 0}[/latex]
Note: [latex]a^m - a^n \neq a^{(m - n)}[/latex]
Example 3.1-b: Simplifying Exponential Expressions Using the Quotient Rule
Express the following as a single power:
- [latex]3^9 \div 3^5[/latex]
- [latex]\displaystyle{\left(\frac{2}{3}\right)^6 \div \left(\frac{2}{3}\right)^4}[/latex]
- [latex](1.15)^5 \div (1.15)^2[/latex]
Solution
- [latex]3^9 \div 3^5 = 3^{(9 - 5)} = 3^4[/latex]
- [latex]\displaystyle{\left(\frac{2}{3}\right)^6 \div \left(\frac{2}{3}\right)^4 = \left(\frac{2}{3}\right)^{6 - 4} =\left(\frac{2}{3}\right)^2}[/latex]
- [latex](1.15)^5 \div (1.15)^2 = (1.15)^{(5 - 2)} = (1.15)^3[/latex]
Power of a Product (Power of a Product Rule)
Each product’s factor is raised to the indicated power to determine a product’s power.
For example,
[latex](3 \times 5)^4 = (3 \times 5)(3 \times 5)(3 \times 5)(3 \times 5)[/latex]
[latex]= 3 \times 3 \times 3 \times 3 \times 5 \times 5 \times 5 \times 5[/latex]
[latex]= 3^4 \times 5^4[/latex]
You will note from the result that each factor of the product is raised to the power of 4.
In general, for any product of factors ‘a’ and ‘b’ that is raised to the power ‘n’,
[latex]\boldsymbol{(a \times b)^n = a^n \times b^n}[/latex]
Example 3.1-c: Expanding Exponential Expressions Using the Power of a Product Rule
Express the following in expanded form using the Power of a Product Rule:
- [latex](8 \times 6)^3[/latex]
- [latex]\displaystyle{\left(\frac{3}{5} \times \frac{2}{7}\right)^3}[/latex]
- [latex](1.12 \times 0.6)^3[/latex]
Solution
- [latex](8 \times 6)^3 = 8^3 \times 6^3[/latex]
- [latex]\displaystyle{\left(\frac{3}{5} \times \frac{2}{7}\right)^3 = \left(\frac{3}{5}\right)^3 \times \left(\frac{2}{7}\right)^3}[/latex]
- [latex](1.12 \times 0.6)^3 = (1.12)^3 \times (0.6)^3[/latex]
Power of a Quotient (Power of a Quotient Rule)
The Power of a Quotient Rule is similar to the Power of a Product Rule. To determine the power of a quotient, raise the numerator to the indicated power and divide by the denominator raised to the indicated power.
For example,
[latex]\displaystyle{\left(\frac{5}{8}\right)^3 = \left(\frac{5}{8}\right) \times \left(\frac{5}{8}\right) \times \left(\frac{5}{8}\right)}[/latex]
[latex]\displaystyle{\frac{5 \times 5 \times 5}{8 \times 8 \times 8} = \frac{5^3}{8^3}}[/latex]
You will note from the result that the numerator and the denominator of the expression is raised to the power of 3.
In general, for any quotient with numerator ‘a’ and non-zero denominator ‘b’ that is raised to the power ‘n’,
[latex]\boldsymbol{\displaystyle{\left(\frac{a}{b}\right)^n = \frac{a^n}{b^n}}}[/latex], where [latex]\boldsymbol{b \neq 0}[/latex]
Example 3.1-d: Expanding Exponential Expressions Using the Power of a Quotient Rule
Express the following in expanded form using the Power of a Quotient Rule:
- [latex]\displaystyle{(\frac{7}{4})^3}[/latex]
- [latex]\left[\frac{\left(\displaystyle{\frac{2}{3}}\right)}{\left(\displaystyle{\frac{3}{5}}\right)}\right]^4[/latex]
- [latex]\displaystyle{\left(\frac{1.05}{0.05}\right)^3}[/latex]
Solution
- [latex]\displaystyle{(\frac{7}{4})^3 = \frac{7^3}{4^3}}[/latex]
- [latex]\left[\frac{\left(\displaystyle{\frac{2}{3}}\right)}{\left(\displaystyle{\frac{3}{5}}\right)}\right]^4 = \displaystyle{\left(\frac{2}{3} \div \frac{3}{5}\right)^4 = \left(\frac{2}{3}\right)^4 \div \left(\frac{3}{5}\right)^4 = \frac{2^4}{3^4} \div \frac{3^4}{5^4}}[/latex]
- [latex]\displaystyle{\left(\frac{1.05}{0.05}\right)^3 = \frac{(1.05)^3}{(0.05)^3}}[/latex]
Power of a Power (Power of a Power Rule)
To determine the power of a power of a number, multiply the two exponents of the powers together to obtain the new exponent of the power.
For example,
[latex](9^3)^2 = (9^3) \times (9^3)[/latex]
[latex]= (9 \times 9 \times 9) \times (9 \times 9 \times 9)[/latex]
[latex]= 9 \times 9 \times 9 \times 9 \times 9 \times 9[/latex]
[latex]= 96[/latex], which is the same as [latex]9^{(3 \times 2)}[/latex]
You will note that the resulting exponent, 6, can be obtained by multiplying the exponents 3 and 2.
In general, to raise the power of a number ‘a’ to a power ‘m’, and then raise it to a power ‘n’, [latex]\boldsymbol{(a^m)^n = a^{(m \times n)}}[/latex]
Example 3.1-e: Simplifying Exponential Expressions Using the Power of a Power Rule
Express the following as a single power:
- [latex](5^4)^3[/latex]
- [latex]\displaystyle{\left[\left(\frac{3}{8}\right)^3\right]^2}[/latex]
- [latex][(1.04)^4]^2[/latex]
Solution
- [latex](5^4)^3 = 5^{(4\times 3)} = 5^{12}[/latex]
- [latex]\displaystyle{\left[\left(\frac{3}{8}\right)^3\right]^2 = \left(\frac{3}{8}\right)^{(3 \times 2)} = \left(\frac{3}{8}\right)^6}[/latex]
- [latex][(1.04)^4]^2 = (1.04)^{(4 \times 2)} = (1.04)^8[/latex]
Example 3.1-f: Solving Expressions Using the Power of a Power Rule, Product Rule, and Quotient Rule
Solve the following:
- [latex](2^2)^3 \times 2^7 \div 2^9[/latex]
- [latex]7^5 \div (7^3)^2 \times 7^2[/latex]
Solution
- [latex](2^2)^3 \times 2^7 \div 2^9 = 2^6 \times 2^7 \div 2^9 = 2^{(6 + 7 - 9)} = 2^4 = 16[/latex]
- [latex]7^5 \div (7^3)^2 \times 7^2 = 7^5 \div 7^6 \times 7^2 = 7^{(5 - 6 + 2)} = 7^1 = 7[/latex]
Table 3.1-a summarizes the properties (rules) of exponents.
Table 3.1-a: Properties (Rules) of Exponents
| Property (Rule) | Rule in Exponential Form |
Example |
|---|---|---|
| Product Rule | [latex]a^m \times a^n = a^{(m + n)}[/latex] | [latex]3^5 \times 3^4 = 3^{(5 + 4)}[/latex] |
| Quotient Rule | [latex]\displaystyle{\frac{a^m}{a^n} = a^{(m - n)}}[/latex] | [latex]\displaystyle{\frac{3^7}{3^4} = 3^{(7 - 4)}}[/latex] |
| Power of a Product Rule | [latex](a \times b)^n = a^n \times b^n[/latex] | [latex](3 \times 5)^2 = 3^2 \times 5^2[/latex] |
| Power of a Quotient Rule | [latex]\displaystyle{\left(\frac{a}{b}\right)^n = \frac{a^n}{b^n}}[/latex] | [latex]\displaystyle{\left(\frac{3}{5}\right)^3 = \frac{3^3}{5^3}}[/latex] |
| Power of a Power Rule | [latex](a^m)^n = a^{(m \times n)}[/latex] | [latex](3^2)^3 = 3^{(2 \times 3)}[/latex] |
Properties of Exponents and Bases of One and Zero
Table 3.1-b summarizes the properties of powers with exponents and bases of one and zero.
Exponents and Bases of One (1) and Zero (0)
| Property (Rule) | Description | Rule in Exponential Form |
Example |
|---|---|---|---|
| Base ‘a’ Exponent 1 | Any base ‘a’ raised to the exponent ‘1’ equals the base itself. | [latex]a^1 = a[/latex] | [latex]8^1 = 8[/latex] |
| Base ‘a’ Exponent 0 | Any non-zero base ‘a’ raised to the exponent ‘0’ equals 1. | [latex]a^0 = 1[/latex] | [latex]8^0 = 1[/latex] |
| Base ‘1’ Exponent ‘n’ | A base of ‘1’ raised to any exponent ‘n’ equals 1. | [latex]1^n = 1[/latex] | [latex]1^5 = 1[/latex] |
| Base ‘0’ Exponent ‘n’ | A base of ‘0’ raised to any positive exponent ‘n’ equals 0. | [latex]0^n = 0[/latex] | [latex]0^5 = 0[/latex] |
| Base ‘0’ Exponent ‘0’ | A base of ‘0’ raised to the exponent ‘0’ is indeterminate. | [latex]0^0 = indeterminate[/latex] | |
Addition and Subtraction of Powers
There is no special rule for powers with the same or different bases for adding and subtracting powers. Evaluate each operation separately and then perform the addition or subtraction.
For example,
- Addition of exponential expressions with the same base: [latex]2^3 + 2^4[/latex]
- Evaluating [latex]2^3[/latex] and [latex]2^4[/latex] separately and then adding, [latex]8 + 16 = 24[/latex]
- Addition of exponential expressions with different bases: [latex]2^2 + 3^3[/latex]
- Evaluating [latex]2^2[/latex] and [latex]3^3[/latex] separately and then adding, [latex]4 + 27 = 31[/latex]
- Subtraction of exponential expressions with the same base: [latex]5^3 - 5^2[/latex]
- Evaluating [latex]5^3[/latex] and [latex]5^2[/latex] separately and then subtracting, [latex]125 - 25 = 100[/latex]
- Subtraction of exponential expressions with different bases: [latex]4^3 - 2^3[/latex]
- Evaluating [latex]4^3[/latex] and [latex]2^3[/latex] separately and then subtracting, [latex]64 - 8 = 56[/latex]
Example 3.1-g: Adding and Subtracting Powers
Evaluate the following:
- [latex]3^3 + 3^2[/latex]
- [latex]5^2 + 3^2[/latex]
- [latex]5^4 - 5^2[/latex]
- [latex]6^2 - 4^2[/latex]
Solution
- [latex]3^3 + 3^2 = 27 + 9 = 36[/latex]
- Note: [latex]\boldsymbol{a^m + a^n \neq a^{(m + n)}}[/latex][latex]3^3 + 3^2 \neq 3^5[/latex]
- [latex]5^2 + 3^2 = 25 + 9 = 34[/latex]
- Note: [latex]\boldsymbol{a^m + b^m \neq (a + b)^m}[/latex][latex]5^2 + 3^2 \neq 8^2[/latex]
- [latex]5^4 - 5^2 = 625 - 25 = 600[/latex]
- Note: [latex]\boldsymbol{a^m - a^n \neq a^{(m - n)}}[/latex][latex]5^4 - 5^2 \neq 5^2[/latex]
- [latex]6^2 - 4^2 = 36 - 16 = 20[/latex]
- Note: [latex]\boldsymbol{a^m - b^m \neq (a - b)^m}[/latex][latex]6^2 - 4^2 \neq 2^2[/latex]
Multiplication and Division of Powers with Different Bases
There is also no special rule for the product or quotient of powers having different bases. Evaluate each operation separately and then perform the multiplication or division.
For example,
- Product of exponential expressions with different bases: [latex]2^4 \times 3^2[/latex]
- Evaluating [latex]2^4[/latex] and [latex]3^2[/latex] separately and then multiplying,[latex]= 16 \times 9 = 144[/latex]
- Quotient of exponential expressions with different bases: [latex]\displaystyle{\frac{3^3}{2^4}}[/latex]
- Evaluating [latex]3^3[/latex] and [latex]2^4[/latex] separately and then dividing,[latex]= \displaystyle{\frac{27}{16} = 1.6875}[/latex]
Example 3.1-h: Multiplying and Dividing Powers that Have Different Bases
Evaluate the following:
- [latex]5^3 \times 4^2[/latex]
- [latex]5^3 \div 3^2[/latex]
- [latex]9^2 \times 5^1[/latex]
- [latex]4^2 \times 5^0[/latex]
Solution
- [latex]5^3 \times 4^2 = 125 \times 16 = 2,000[/latex]
- [latex]\displaystyle{5^3 \div 3^2 = 125 ÷ 9 = \frac{125}{9} = 13\frac{8}{9}}[/latex]
- [latex]9^2 \times 5^1 = 81 \times 5 = 405[/latex]
- [latex]4^2 \times 5^0 = 16 \times 1 = 16[/latex]
Multiplication and Division of Powers with Different Bases
The exponent key on different calculators can be identified by symbols such as  ,
,  ,
,  , etc.
, etc.
In the following examples ‘ ’ will be used to represent the exponent key.
’ will be used to represent the exponent key.
Example 3.1-i: Evaluating Exponential Expressions using a Calculator
Evaluate the following using a calculator:
- [latex]5^6[/latex]
- [latex]\displaystyle{\left(\frac{3}{2}\right)^3}[/latex]
- [latex](1.02)^4[/latex]
Solution
3.1 Exercises
Answers to the odd-numbered problems are available at the end of the textbook.
For problems 1 and 2, identify the values in the empty cells for Repeated Multiplication, Base, Exponent, and Power (Exponential Notation).
-
Question Repeated Multiplication Base Exponent Power
(Exponential Notation)a. [latex]7 \times 7 \times 7 \times 7[/latex] Empty cell Empty cell Empty cell b. Empty cell Empty cell Empty cell [latex]9^5[/latex] c. Empty cell [latex]3[/latex] [latex]4[/latex] Empty cell d. [latex]\displaystyle{\frac{2}{5} \times \frac{2}{5} \times \frac{2}{5} \times \frac{2}{5} \times \frac{2}{5} \times \frac{2}{5}}[/latex] Empty cell Empty cell Empty cell e. Empty cell Empty cell Empty cell [latex]\displaystyle{\left(\frac{5}{7}\right)^5}[/latex] f. Empty cell [latex]\displaystyle{\left(\frac{4}{7}\right)}[/latex] [latex]3[/latex] Empty cell g. [latex](1.15) \times (1.15) \times (1.15) \times (1.15)[/latex] Empty cell Empty cell Empty cell h. Empty cell Empty cell Empty cell [latex](1.6)^3[/latex] i. Empty cell [latex](1.25)[/latex] [latex]5[/latex] Empty cell -
Question Repeated Multiplication Base Exponent Power
(Exponential Notation)a. [latex]2 \times 2 \times 2 \times 2 \times 2 \times 2 \times 2 \times 2[/latex] Empty cell Empty cell Empty cell b. Empty cell Empty cell Empty cell [latex]6^7[/latex] c. Empty cell [latex]5[/latex] [latex]3[/latex] Empty cell d. [latex]\displaystyle{\frac{2}{7} \times \frac{2}{7} \times \frac{2}{7} \times \frac{2}{7} \times \frac{2}{7}}[/latex] Empty cell Empty cell Empty cell e. Empty cell Empty cell Empty cell [latex]\displaystyle{\left(\frac{3}{8}\right)^4}[/latex] f. Empty cell [latex]\displaystyle{\left(\frac{2}{9}\right)}[/latex] [latex]4[/latex] Empty cell g. [latex](2.5) \times (2.5) \times (2.5) \times (2.5) \times (2.5)[/latex] Empty cell Empty cell Empty cell h. Empty cell Empty cell Empty cell [latex](1.1)^5[/latex] i. Empty cell [latex](0.75)[/latex] [latex]4[/latex] Empty cell
Express problems 3 to 22 as a single power and then evaluate using a calculator. Round the answer to two decimal places, wherever applicable.
- [latex]4^3 \times 4^6[/latex]
- [latex]5^5 \times 5^6[/latex]
- [latex]\displaystyle{\left(\frac{1}{2}\right)^4\left(\frac{1}{2}\right)^3}[/latex]
- [latex]\displaystyle{\left(\frac{2}{3}\right)^2\left(\frac{2}{3}\right)^3}[/latex]
- [latex]\displaystyle{\left(\frac{5}{2}\right)^2\left(\frac{5}{2}\right)^3}[/latex]
- [latex]\displaystyle{\left(\frac{5}{3}\right)^3\left(\frac{5}{3}\right)^2}[/latex]
- [latex](3.25)^4(3.25)^2[/latex]
- [latex](0.75)^3(0.75)^4[/latex]
- [latex]6^8 \div 6^3[/latex]
- [latex]3^7 \div 3^5[/latex]
- [latex]\displaystyle{\left(\frac{2}{5}\right)^3 \div \left(\frac{2}{5}\right)^1}[/latex]
- [latex]\displaystyle{\left(\frac{3}{2}\right)^4 \div \left(\frac{3}{2}\right)^3}[/latex]
- [latex](1.4)^5 \div (1.4)^2[/latex]
- [latex](3.25)^6 \div (3.25)^5[/latex]
- [latex][(6)^2]^3[/latex]
- [latex][(5)^3]^2[/latex]
- [latex]\displaystyle{\left[\left(\frac{2}{3}\right)^4\right]^3}[/latex]
- [latex]\displaystyle{\left[\left(\frac{3}{4}\right)^4\right]^2}[/latex]
- [latex][(2.5)^2]^3[/latex]
- [latex][(1.03)^3]^2[/latex]
Express problems 23 to 34 as a power of the indicated base value.
- [latex]4^5[/latex] as a power of 2
- [latex]9^6[/latex] as a power of 3
- [latex]9(27)^2[/latex] as a power of 3
- [latex]8(16)^2[/latex] as a power of 2
- [latex]\displaystyle{\frac{3^9 \times 3^2}{3^5}}[/latex] as a power of 3
- [latex]\displaystyle{\frac{2^9 \times 2^1}{2^5}}[/latex] as a power of 2
- [latex]\displaystyle{\frac{(2^5)^4}{4^6}}[/latex] as a power of 2
- [latex]\displaystyle{\frac{(2^5)^4}{16^3}}[/latex] as a power of 2
- [latex]\displaystyle{\frac{10^6}{10^0}}[/latex] as a power of 10
- [latex]\displaystyle{\frac{3^7}{27}}[/latex] as a power of 3
- [latex]\displaystyle{\frac{8^5}{8^3}}[/latex] as a power of 2
- [latex]\displaystyle{\frac{5^6}{125}}[/latex] as a power of 5
Evaluate problems 35 to 70.
- [latex]5^2 + 5^3[/latex]
- [latex]4^3 + 4^2[/latex]
- [latex]5^4 - 2^4[/latex]
- [latex]6^3 - 4^3[/latex]
- [latex]4^4 - 4^2[/latex]
- [latex]6^3 - 6^1[/latex]
- [latex]7^2 + 3^2[/latex]
- [latex]6^2 - 4^2[/latex]
- [latex]3^5 + 5^3[/latex]
- [latex]4^3 + 3^4[/latex]
- [latex]2^5 - 5^2[/latex]
- [latex]2^6 - 6^2[/latex]
- [latex]5^4 - 4^2[/latex]
- [latex]10^3 - 7^2[/latex]
- [latex]4^0 + 4^4[/latex]
- [latex]3^0 + 3^4[/latex]
- [latex](5 \times 4)^3[/latex]
- [latex](10 \times 2)^4[/latex]
- [latex](1.25 \times 4)^4[/latex]
- [latex](5 \times 0.8)^3[/latex]
- [latex]\displaystyle{\left(\frac{2}{3} + 6\right)^5}[/latex]
- [latex]\displaystyle{\left(\frac{3}{5} + 1\right)^3}[/latex]
- [latex]3^4 + 3^2 + 3^0[/latex]
- [latex]4^2 + 4^4 + 4^0[/latex]
- [latex]2^4 + 3^4 - 1^4[/latex]
- [latex]3^3 + 2^3 - 1^3[/latex]
- [latex]\displaystyle{\left(\frac{1}{2}\right)^3 + \left(\frac{1}{2}\right)^2 + \left(\frac{1}{2}\right)^0}[/latex]
- [latex]\displaystyle{\left(\frac{1}{5}\right)^2 + \left(\frac{1}{5}\right)^0 + \left(\frac{1}{5}\right)^4}[/latex]
- [latex](2.1)^2 + (2.1)^0[/latex]
- [latex](3.2)^2 + (3.2)^1[/latex]
- [latex]4^3 \times 3^4[/latex]
- [latex]7^2 \times 2^2[/latex]
- [latex]6^4 ÷ 5^4[/latex]
- [latex]8^2 ÷ 7^2[/latex]
- [latex](2 \times 3^2)^4[/latex]
- [latex](5 \times 2^2)^3[/latex]
Unless otherwise indicated, this chapter is an adaptation of the eTextbook Foundations of Mathematics (3rd ed.) by Thambyrajah Kugathasan, published by Vretta-Lyryx Inc., with permission. Adaptations include supplementing existing material and reordering chapters.






