2.1 Decimal Numbers
Decimal numbers, also known as decimals, represent a part or a portion of a whole.
Decimal numbers are used in situations requiring more precision than whole numbers. We use decimal numbers frequently in our daily lives; a good example of this is money. For example, a nickel is worth 5¢, equal to $0.05, and the bus fare for a city may be $3.25; 0.05 and 3.25 are examples of decimal numbers.
A decimal number contains a whole number portion and a decimal portion. The decimal point (.) is used to separate these two portions: the whole number portion is comprised of the digits to the left of the decimal point, and the decimal portion is comprised of the digits to the right of the decimal point. The decimal portion represents a value less than 1.
For example,
The decimal portion of a decimal can be represented as a fraction with a denominator that is a power of 10 (i.e., 10, 100, 1,000, etc.). These fractions are referred to as decimal fractions.
For example,
- The decimal number 0.3 is [latex]\displaystyle{\frac{3}{10}}[/latex] as a decimal fraction.
- The decimal number 0.07 is [latex]\displaystyle{\frac{7}{100}}[/latex] as a decimal fraction.
- The decimal portion of the decimal number 345.678 is [latex]\displaystyle{\frac{678}{1,000}}[/latex] as a decimal fraction.
When decimal numbers are expressed as a decimal fraction with a denominator that is a power of 10, we do not reduce to their lowest terms.
For example, [latex]\displaystyle{\frac{678}{1,000}}[/latex] if reduced to [latex]\displaystyle{\frac{339}{500}}[/latex]is no longer expressed with a denominator that is a power of 10, and therefore is not a decimal fraction.
Similarly,
- [latex]1.2 = 1\frac{2}{10}[/latex]
- [latex]23.45 = 23\frac{45}{100}[/latex]
- [latex]75.378 = 75\frac{378}{1,000}[/latex]
Every whole number can be written as a decimal number by placing a decimal point to the right of the unit's digits.
For example, the whole number 5 written as a decimal number is 5. or 5.0 or 5.00, etc.
The number of decimal places in a decimal number is the number of digits written to the right of the decimal point.
For example,
- 5. No decimal places
- 5.0 One decimal place
- 5.00 Two decimal places
- 1.250 Three decimal places
- 2.0050 Four decimal places
Types of Decimal Numbers
There are three different types of decimal numbers.
- Non-repeating, terminating decimals numbers:
For example, 0.2, 0.3767, 0.86452 - Repeating, non-terminating decimal numbers:
For example, 0.222222.... (0.2), 0.255555.... (0.25), 0.867867.... (0.867) - Non-repeating, non-terminating decimal numbers:
For example, 0.453740...., π (3.141592...), e (2.718281...)
Place Value of Decimal Numbers
The position of each digit in a decimal number determines the place value of the digit. Exhibit 2.1 illustrates the place value of the five-digit decimal number: 0.35796.
The place value of each digit as you move right from the decimal point is found by decreasing powers of 10. The first place value to the right of the decimal point is the tenths place; the second place value is the hundredths place, and so on, as shown in Table 2.1-b.
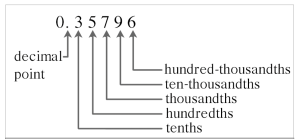
Place Value Chart of Decimal Numbers
| Exponent and Fractional Equivalent | Decimal Form | Place Value |
|---|---|---|
| [latex]10^{-1} = \displaystyle{\frac{1}{10}}[/latex] | 0.1 | Tenths |
| [latex]10^{-2} = \displaystyle{\frac{1}{100}}[/latex] | 0.01 | Hundredths |
| [latex]10^{-3} = \displaystyle{\frac{1}{1,000}}[/latex] | 0.001 | Thousandths |
| [latex]10^{-4} = \displaystyle{\frac{1}{10,000}}[/latex] | 0.0001 | Ten-thousandths |
| [latex]10^{-5} = \displaystyle{\frac{1}{100,000}}[/latex] | 0.00001 | Hundred-thousandths |
The five-digit number in Exhibit 2.1 is written as 0.35796 in its standard form.
| Digit | Place Value |
|---|---|
| 0. | The whole number in front of the decimal point. |
| 3 | Tenths |
| 5 | Hundredths |
| 7 | Thousandths |
| 9 | Ten-thousandths |
| 6 | Hundred-thousandths |
The decimal number 0.35796 can also be written in expanded form as follows:
[latex]0.3 + 0.05 + 0.007 + 0.0009 + 0.00006[/latex]
Or,
3 tenths + 5 hundredths + 7 thousandths + 9 ten-thousandths + 6 hundred-thousandths
Or,
[latex]\displaystyle{\frac{3}{10} + \frac{5}{100} + \frac{7}{1,000} + \frac{9}{10,000} + \frac{6}{100,000}}[/latex]
(0.35796 as a decimal fraction is [latex]\displaystyle{\frac{35,796}{100,000}}[/latex])
Reading and Writing Decimal Numbers
Follow these steps to read and write decimal numbers in word form:
- Read or write the number to the left of the decimal point as a whole number.
- Read or write the decimal point as “and".
- Read or write the number to the right of the decimal point as a whole number, followed by the name of the place value occupied by the right-most digit.
For example, 745.023 is written in word form as:
As noted below, there are other ways of reading and writing decimal numbers.
- Use “point” to indicate the decimal point and read or write each digit individually. For example, 745.023 can be read or written as seven hundred forty-five point zero, two, three.
- Ignore the decimal point of the decimal number and read or write the number as a whole number followed by the name of the place value occupied by the right-most digit of the decimal portion. For example, 745.023 can also be read or written as seven hundred forty-five thousand, twenty-three thousandths.
(i.e., [latex]\displaystyle{\frac{745,023}{1,000}}[/latex]).
Note: The above two representations are not used in this chapter's examples and exercise questions.
Use of Hyphens to Express Decimal Numbers in Word Form
- A hyphen ( - ) is used to express the two-digit numbers 21 to 29, 31 to 39, 41 to 49, … 91 to 99 in each group in their word form.
- A hyphen ( - ) is also used while expressing the place value portion of a decimal number, such as ten-thousandths, hundred-thousandths, ten-millionths, hundred-millionths, and so on.
The following examples illustrate the use of hyphens to express numbers in their word form:
- 0.893 Eight hundred ninety-three thousandths
- 0.0506 Five hundred six ten-thousandths
- 0.00145 One hundred forty-five hundred-thousandths
Example 2.1-a: Writing Decimal Numbers in Standard Form
Write the following decimal numbers in standard form:
- Two hundred and thirty-five hundredths
- Three and seven tenths
- Eighty-four thousandths
Solution
-
200 (whole number portion)
and [latex]\displaystyle{\frac{35}{100} = 0.35}[/latex] (decimal portion)
Therefore, the number is written in standard form as 200.35. -
3 (whole number portion)
and [latex]\displaystyle{\frac{7}{10} = 0.7}[/latex] (decimal portion)
Therefore, the number is written in standard form as 3.7. -
0 (whole number portion)
and [latex]\displaystyle{\frac{84}{1,000} = 0.084}[/latex] (decimal portion)
Therefore, the number is written in standard form as 0.084.
Example 2.1-b: Writing Decimal Numbers in Word Form
Write the following decimal numbers in word form:
- 23.125
- 7.43
- 20.3
- 0.2345
Solution
-
23.125
The last digit, 5, is in the thousandths place.
[latex]\displaystyle{= 23\frac{125}{1,000}}[/latex]
Twenty-three and one hundred twenty-five thousandths
-
7.43
The last digit, 3, is in the hundredths place.
[latex]\displaystyle{= 7\frac{43}{100}}[/latex]
Seven and forty-three hundredths
-
20.3
The last digit, 3, is in the tenths place.
[latex]\displaystyle{= 20\frac{3}{10}}[/latex]
Twenty and three tenths
-
0.2345
The last digit, 5, is in the ten-thousandths place.
[latex]\displaystyle{= \frac{2,345}{10,000}}[/latex]
Two thousand, three hundred forty-five ten-thousandths
Rounding Decimal Numbers
Rounding Decimal Numbers to the Nearest Whole Number, Tenth, Hundredth, etc.
Rounding decimal numbers refers to changing the value of the decimal number to the nearest whole number, tenth, hundredth, thousandth, etc. It is also called rounding to a specific number of decimal places, indicating the number of decimal places left when the rounding is complete.
- Rounding to the nearest whole number is the same as rounding without decimals.
- Rounding to the nearest tenth is the same as rounding to one decimal place.
- Rounding to the nearest hundredth is the same as rounding to two decimal places.
- Rounding to the nearest cent refers to rounding the amount to the nearest hundredth, the same as rounding to two decimal places.
Follow these steps to round decimal numbers:
- Identify the digit to be rounded (this is the place value for which the rounding is required).
- If the digit to the immediate right of the identified rounding digit is less than 5 (0, 1, 2, 3, 4), do not change the value of the rounding digit.
If the digit to the immediate right of the identified rounding digit is 5 or greater than 5 (5, 6, 7, 8, 9), increase the value of the rounding digit by one (i.e., round up by one number). - Drop all digits to the right of the rounding digit.
Example 2.1-c: Rounding Decimal Numbers
Round the following decimal numbers to the indicated place value:
- 268.143 to the nearest tenth
- 489.679 to the nearest hundredth
- $39.9985 to the nearest cent
Solution
-
Rounding 268.143 to the nearest tenth:
1 is the rounding digit in the tenths place: 268.143.
The digit to the immediate right of the rounding digit is less than 5; therefore, do not change the value of the rounding digit. Drop all of the digits to the right of the rounding digit. This will result in 268.1.
Therefore, 268.143 rounded to the nearest tenth is 268.1.
-
Rounding 489.679 to the nearest hundredth:
7 is the rounding digit in the hundredths place: 489.679.
The digit to the immediate right of the rounding digit is greater than 5; therefore, increase the value of the rounding digit by one, from 7 to 8, and drop all of the digits to the right of the rounding digit. This will result in 489.68.
Therefore, 489.679 rounded to the nearest hundredth is 489.68.
-
Rounding $39.9985 to the nearest cent:
9 is the rounding digit in the hundredths place: $39.9985.
The digit to the immediate right of the rounding digit is greater than 5; therefore, increase the value of the rounding digit by one, from 9 to 10, by replacing the rounding digit 9 with 0 and carrying the one to the tenths place, then to the ones, and then to the tens, to increase the digit 3 to 4. Finally, drop all digits that are to the right of the rounding digit. This will result in $40.00.
Therefore, $39.9985 rounded to the nearest cent is $40.00.
2.1 Exercises
Answers to odd-numbered problems are available at the end of the textbook.
- a. [latex]\displaystyle{\frac{6}{10}}[/latex]
b. [latex]\displaystyle{\frac{7}{1,000}}[/latex] - a. [latex]\displaystyle{\frac{9}{10,000}}[/latex]
b. [latex]\displaystyle{\frac{41}{1,000}}[/latex] - a. [latex]\displaystyle{\frac{12}{100}}[/latex]
b. [latex]\displaystyle{\frac{29}{1,000}}[/latex] - a. [latex]\displaystyle{\frac{75}{100}}[/latex]
b. [latex]\displaystyle{\frac{3}{10}}[/latex] - a. [latex]7\frac{5}{10}[/latex]
b. [latex]9\frac{503}{1,000}[/latex] - a. [latex]9\frac{3}{10}[/latex]
b. [latex]6\frac{207}{1,000}[/latex] - a. [latex]\displaystyle{\frac{367}{100}}[/latex]
b. [latex]\displaystyle{\frac{2,567}{1,000}}[/latex] - a. [latex]\displaystyle{\frac{475}{10}}[/latex]
b. [latex]\displaystyle{\frac{2,972}{1,000}}[/latex]
- Eighty-seven and two tenths
- Thirty-five and seven tenths
- Three and four hundredths
- Nine and seven hundredths
- Four hundred one ten-thousandths
- Fifty-two and three hundred five thousandths
- Eighty-nine and six hundred twenty-five ten-thousandths
- Two hundred eight thousandths
- One thousand, seven hundred eighty-seven and twenty-five thousandths
- Seven thousand, two hundred sixty and fifteen thousandths
- Four hundred twelve and sixty-five hundredths
- Nine hundred eighty-seven and twenty hundredths
- One million, six hundred thousand and two hundredths
- Six million, two hundred seventeen thousand and five hundredths
- Twenty-three and five-tenths
- Twenty-nine hundredths
- a. 42.55
b. 734.125 - a. 7.998
b. 12.77 - a. 0.25
b. 9.5 - a. 0.987
b. 311.2 - a. 7.07
b. 15.002 - a. 11.09
b. 9.006 - a. 0.062
b. 0.054 - a. 0.031
b. 0.073
- 0.034, 0.403, 0.043, 0.304
Arrange the following decimal numbers from least to greatest.
- 1.014, 1.011, 1.104, 1.041
- 415.1654
- 7.8725
- 264.1545
- 25.5742
- 24.1575
- 112.1255
- 10.3756
- 0.9753
- 14.3585
- 19.6916
- 181.1267
- $10.954
- $16.775
- $24.995
- $9.987
Unless otherwise indicated, this chapter is an adaptation of the eTextbook Foundations of Mathematics (3rd ed.) by Thambyrajah Kugathasan, published by Vretta-Lyryx Inc., with permission. Adaptations include supplementing existing material and reordering chapters.



