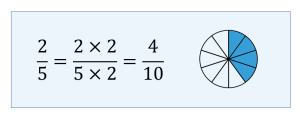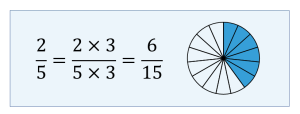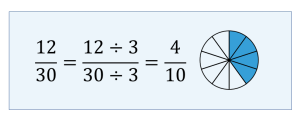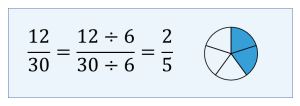2.3 Fractions

If we divide one whole unit into several equal portions, then one or more of these equal portions can be represented by a fraction.

A fraction is composed of the following three parts:

  1. Numerator: the number of equal parts of a whole unit.
  2. Fraction bar: the division sign, meaning ‘divided by’.
  3. Denominator: the total number of equal parts into which the whole unit is divided.

For example, [latex]\displaystyle{\frac{3}{8}}[/latex] is a fraction.

Fraction 3/8 illustrated by a circle divided into 8 equal parts with 3 shaded.

The numerator ‘3’ indicates that the fraction represents 3 equal parts of a whole unit, and the denominator ‘8’ indicates that the whole unit is divided into 8 equal parts, as shown above. The fraction bar indicates that the numerator ‘3’ is divided by the denominator ‘8’.

[latex]\displaystyle{\frac{3}{8}}[/latex] is read as “three divided by eight”, “three-eighths”, or “three over eight”. All of these indicate that 3 is the numerator, 8 is the denominator, and the fraction represents 3 of 8 pieces of the whole. The numerator and denominator are referred to as the terms of the fraction.

Note: The denominator of a fraction cannot be zero since a number cannot be divided into zero equal parts.

Any number that can be represented as a fraction is known as a rational number.

For example,

  • [latex]\displaystyle{\frac{2}{3}}[/latex], [latex]\displaystyle{\frac{5}{2}}[/latex], and [latex]\displaystyle{\frac{7}{1}}[/latex] are rational numbers.
  • The whole number 7 can be written as the fraction [latex]\displaystyle{\frac{7}{1}}[/latex]; therefore, 7 is also a rational number.

Fractions can be represented on a number line. They are plotted in-between whole numbers.

For example, [latex]\displaystyle{\frac{1}{2}}[/latex] is represented on a number line as:

When one unit is divided into two equal portions, each portion represents one-half of that unit. One of such equal portions is written as [latex]\displaystyle{\frac{1}{2}}[/latex].

Fraction 1/2 placed on a number line between 0 and 1 with an arrow pointing right.

Example 2.3-a: Representing Fractions on a Number Line

Represent the following fractions on a number line:

  1. [latex]\displaystyle{\frac{2}{3}}[/latex]
  2. [latex]\displaystyle{\frac{3}{5}}[/latex]

Solution

  1. When one unit is divided into three equal portions, each portion represents one-third of that unit. Two of such equal portions is two-thirds and is written as [latex]\displaystyle{\frac{2}{3}}[/latex].

     

    Example 2.1-a Solution a. Two-thirds plotted on a number line as described in the text above.

  2. When one unit is divided into five equal portions, each portion represents one-fifth of that unit. Three of such equal portions is three-fifths and is written as [latex]\displaystyle{\frac{3}{5}}[/latex].

     

    Example 2.1-a Solution b. Three-fifths plotted on a number line as described in the text above.

Types of Fractions

Proper Fractions

A proper fraction is a fraction in which the numerator is less than the denominator.

For example,

  • [latex]\displaystyle{\frac{3}{8}}[/latex] is a proper fraction because the numerator, 3, is less than the denominator, 8.
    three-eighths illustrated by a circle divided into 8 equal parts. Three of those parts are shaded.

Improper Fractions

An improper fraction is a fraction in which the numerator is greater than or equal to the denominator; i.e., the value of the entire fraction is more than 1.

For example,

  • [latex]\displaystyle{\frac{7}{4}}[/latex] is an improper fraction because the numerator 7 is greater than the denominator 4
    (i.e., 7 > 4, or [latex]\displaystyle{\frac{7}{4}}[/latex] > 1).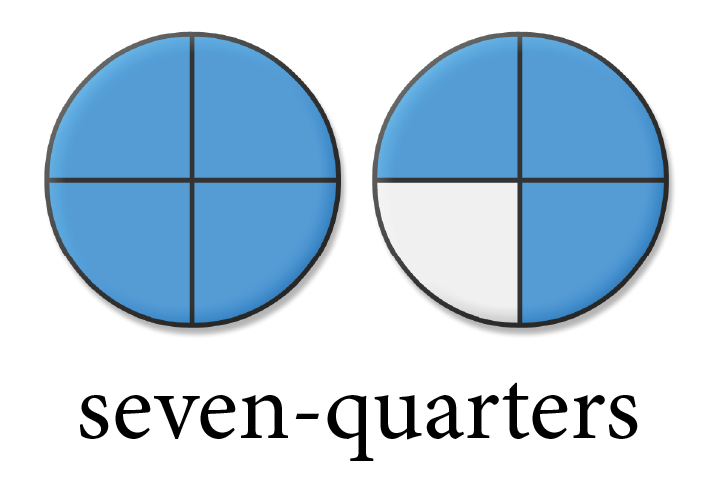
    Seven-quarters illustrated by two circles each divided into 4 equal parts (8 parts in total). 7 of those parts are shaded.

Mixed Numbers (or Mixed Fractions)

A mixed number consists of both a whole number and a proper fraction, written side-by-side, which implies that the whole number and the proper fraction are added.

For example,

  • [latex]3{\frac{5}{8}}[/latex] is a mixed number, where 3 is the whole number, and [latex]\displaystyle{\frac{5}{8}}[/latex] is the proper fraction.
    [latex]3{\frac{5}{8}}[/latex] implies 3 + [latex]\displaystyle{\frac{5}{8}}[/latex]
    Three and five-eighths illustrated with 4 circles each divided into 8 equal parts. Three circles are completely shaded and 5 parts of the 4th circle are shaded to show 3 and Five-eighths.

Relationship Between Mixed Numbers and Improper Fractions

Converting a Mixed Number to an Improper Fraction

Follow these steps to convert a mixed number to an improper fraction:

Step 1: Multiply the whole number by the fraction’s denominator and add this value to the fraction’s numerator.

Step 2: The resulting answer will be the numerator of the improper fraction.

Step 3: The denominator of the improper fraction is the same as the denominator of the original fraction in the mixed number.

Example: Convert [latex]3{\frac{5}{8}}[/latex] to an improper fraction.

Step 1: 3(8) = 24

Step 2: 24 + 5 = 29. The numerator will be 29.

Step 3: The denominator will be 8.
Therefore, [latex]3{\frac{5}{8}}[/latex] = [latex]\displaystyle{\frac{29}{8}}[/latex]

Note: You can perform the above steps in a single line of arithmetic as follows:

[latex]3{\frac{5}{8}}[/latex] = [latex]\displaystyle{\frac{3(8) + 5}{8}}[/latex] = [latex]\displaystyle{\frac{24 + 5}{8}}[/latex] = [latex]\displaystyle{\frac{29}{8}}[/latex]

Four circles are divided into 8 equal pieces. Three of the four circles are completely shaded, and five pieces of the last circle are shaded for 29 pieces.

3 × 8 = 24 plus 5 pieces for a total of 29 pieces. Three and five-eighths illustrated with 4 circles each divided into 8 equal parts. Three circles are completely shaded and 5 parts of the 4th circle are shaded to show 3 and Five-eighths.

Converting an Improper Fraction to a Mixed Number

Follow these steps to convert an improper fraction to a mixed number:

Step 1: Divide the numerator by the denominator.

Step 2: The quotient becomes the whole number, and the remainder becomes the numerator of the fraction portion of the mixed number.

Step 3: The denominator of the fraction portion of the mixed number is the same as the denominator of the original improper fraction.

Example: Convert [latex]\displaystyle{\frac{29}{8}}[/latex] to an improper fraction.

Step 1: Divide 29 by 8.

Step 2: The quotient (3) becomes the whole number, and the remainder (5) becomes the numerator of the fraction portion of the mixed number.

Step 3: The denominator of the fraction portion of the mixed number (8) is the same as the denominator of the original improper fraction (8).

[latex]\begin{array}{r} 3 &&\hbox{Quotient}\\ 8\enclose{longdiv}{29}\\ -24  \\ \hline 5 &&\hbox{Remainder}\\ \end{array}[/latex]

Therefore, [latex]\displaystyle{\frac{29}{8}}[/latex] = [latex]3{\frac{5}{8}}[/latex]

Equivalent Fractions

When a fraction’s numerator and denominator are either multiplied by the same number or divided by the same number, the result is a new fraction known as an equivalent fraction. Equivalent fractions have the same value.

That is, the same part (or portion) of a whole unit can be represented by different fractions.

For example,

Starting with the fraction 1/2 showing a circle divided into 2 parts with 1 part shaded. Multiplying by 2 creates the next equivalent fraction 2/4. A circle divided into 4 parts with 2 parts shaded. Multiplying by 2 again creates the next equivalent fraction 3/6. A circle divided into 6 parts with 3 parts shaded. Multiplying by 2 again creates the next equivalent fraction 4/8. A circle divided into 8 parts with 4 parts shaded. Multiplying by 2 again creates the last equivalent fraction 5/10. A circle divided into 10 parts with 5 parts shaded.

[latex]\displaystyle{\frac{1}{2}}[/latex], [latex]\displaystyle{\frac{2}{4}}[/latex], [latex]\displaystyle{\frac{3}{6}}[/latex], [latex]\displaystyle{\frac{4}{8}}[/latex], [latex]\displaystyle{\frac{5}{10}}[/latex], … are equivalent fractions.

 

Example 2.3-b: Finding Equivalent Fractions by Raising to Higher Terms

Find two equivalent fractions of [latex]\displaystyle{\frac{2}{5}}[/latex] by raising to higher terms.

Solution

To find an equivalent fraction of [latex]\displaystyle{\frac{2}{5}}[/latex], multiply both the numerator and denominator by 2. The resulting equivalent fraction is [latex]\displaystyle{\frac{4}{10}}[/latex].

An equivalent fraction of 2/5 is found by multiplying the top and bottom by 2. The resulting fraction is 4/10. The pie chart shows 4 of the 10 slices shaded.

To find an equivalent fraction of [latex]\displaystyle{\frac{2}{5}}[/latex], multiply both the numerator and denominator by 3. The resulting equivalent fraction is [latex]\displaystyle{\frac{6}{15}}[/latex].

An equivalent fraction of 2/5 is found by multiplying the top and bottom by 3. The resulting fraction is 6/15. The pie chart shows 6 of the 15 slices shaded.

Therefore, [latex]\displaystyle{\frac{4}{10}}[/latex] and [latex]\displaystyle{\frac{6}{15}}[/latex] are equivalent fractions of [latex]\displaystyle{\frac{2}{5}}[/latex].

Example 2.3-c: Finding Equivalent Fractions by Reducing to Lower Terms

Find two equivalent fractions of [latex]\displaystyle{\frac{12}{30}}[/latex] by reducing to lower terms.

Solution

To find an equivalent fraction of [latex]\displaystyle{\frac{12}{30}}[/latex], divide both the numerator and denominator by 3. The resulting equivalent fraction is [latex]\displaystyle{\frac{4}{10}}[/latex].

An equivalent fraction of 4/10 is found by dividing the top and bottom by 3. The resulting fraction is 4/10. The pie chart shows 4 of the 10 slices shaded.
To find another equivalent fraction, divide the numerator and denominator by 2. The resulting equivalent fraction is [latex]\displaystyle{\frac{2}{5}}[/latex].
An equivalent fraction of 2/5 is found bydividing the top and bottom by 2. The resulting fraction is 2/5. The pie chart shows 2 of the 5 slices shaded.
Or, the lowest terms can be found by dividing both the numerator and denominator of the original fraction, [latex]\displaystyle{\frac{12}{30}}[/latex], by 6.
An equivalent fraction of 2/5 is found by dividing the top and bottom by 6. The resulting fraction is 2/5. The pie chart shows 2 of the 5 slices shaded.

Therefore, [latex]\displaystyle{\frac{4}{10}}[/latex] and [latex]\displaystyle{\frac{2}{5}}[/latex] are equivalent fractions of [latex]\displaystyle{\frac{12}{30}}[/latex].

Note: The fraction [latex]\displaystyle{\frac{2}{5}}[/latex] cannot be further reduced, as 2 and 5 do not have any common factors.
Therefore, [latex]\displaystyle{\frac{2}{5}}[/latex] is a fraction in its lowest (or simplest) terms. We will learn more about this further in the section.

Identifying Equivalent Fractions Using Cross Products

If the cross products of two fractions are equal, then the two fractions are equivalent fractions, and vice versa (i.e., if the fractions are equivalent, then their cross products are equal).

That is, if [latex]\displaystyle{\frac{a}{b}}[/latex] = [latex]\displaystyle{\frac{c}{d}}[/latex], then a × d = b × c

a × d and b × c  are known as cross products

For example, [latex]\displaystyle{\frac{3}{5}}[/latex] and [latex]\displaystyle{\frac{12}{20}}[/latex] are equivalent fractions because their cross products, 3 × 20 and 5 × 12, are equal:

3 × 20 = 60

5 × 12 = 60

Example 2.3-d: Classifying Fractions as Equivalent or Not Equivalent

Classify the pair of fractions as ‘equivalent’ or ‘not equivalent’ by using their cross products.

  1. [latex]\displaystyle{\frac{2}{5}}[/latex] and [latex]\displaystyle{\frac{12}{20}}[/latex]
  2. [latex]\displaystyle{\frac{5}{4}}[/latex] and [latex]\displaystyle{\frac{20}{12}}[/latex]
  3. [latex]\displaystyle{\frac{3}{8}}[/latex] and [latex]\displaystyle{\frac{9}{24}}[/latex]

Solution

  1. [latex]\displaystyle{\frac{2}{5}}[/latex] and [latex]\displaystyle{\frac{12}{20}}[/latex]

    The cross products are 2 × 30 and 5 × 12.

    2 × 30 = 60

    5 × 12 = 60

    Therefore, the two fractions are equivalent.

    The cross-products are equal.

  2. [latex]\displaystyle{\frac{5}{4}}[/latex] and [latex]\displaystyle{\frac{20}{12}}[/latex]

    The cross products are 5 × 12 and 4 × 20.

    5 × 12 = 60

    4 × 20 = 80

    Therefore, the two fractions are not equivalent.

    The cross products are not equal.

  3. [latex]\displaystyle{\frac{3}{8}}[/latex] and [latex]\displaystyle{\frac{9}{24}}[/latex]

    The cross products are 3 × 24 and 8 × 9.

    3 × 24 = 72

    8 × 9 = 72

    Therefore, the two fractions are equivalent.

    The cross-products are equal.

Fractions in Lowest (or Simplest) Terms

Dividing a fraction’s numerator and denominator by the same number, which results in an equivalent fraction, is known as reducing or simplifying the fraction.

For example, we saw in Example 2.1-c that [latex]\displaystyle{\frac{4}{10}}[/latex] and [latex]\displaystyle{\frac{2}{5}}[/latex] are reduced fractions of [latex]\displaystyle{\frac{12}{30}}[/latex].

A fraction in which the numerator and denominator have no factors in common (other than 1) is said to be a fraction in its lowest (or simplest) terms.

Any fraction can be fully reduced to its lowest terms by one of the following two methods:

Method 1: Dividing the numerator and denominator by the greatest common factor (GCF).

Method 2: Writing the numerator and denominator as products of prime factors and reducing by the common prime factors.

Example 2.3-e: Reducing Fractions to their Lowest Terms

Reduce the following fractions to their lowest terms.

  1. [latex]\displaystyle{\frac{40}{45}}[/latex]
  2. [latex]\displaystyle{\frac{54}{24}}[/latex]

Solution

a. [latex]\displaystyle{\frac{40}{45}}[/latex]

Method 1: Factors of 40 are: 1, 2, 4, 5, 8, 10, 20, and 40. Factors of 45 are: 1, 3, 5, 9, 15, and 45. The GCF is 5. Dividing the numerator and denominator by the GCF, 5,

[latex]\displaystyle{\frac{40}{45} = \frac{40 ÷ 5}{45 ÷ 5} = \frac{8}{9}}[/latex]

Method 2: Prime factors of 40 are: 2 × 2 × 2 × 5. Prime factors of 45 are: 3 × 3 × 5. The common prime factor is one 5. Therefore, [latex]\displaystyle{\frac{40}{45}}[/latex] is equal to [latex]\displaystyle{\frac{8}{9}}[/latex] reduced to its lowest terms.

b. [latex]\displaystyle{\frac{54}{24}}[/latex]

Method 1: Factors of 54 are: 1, 2, 3, 6, 9, 18, 27, and 54. Factors of 24 are: 1, 2, 3, 4, 6, 8, 12, and 24. The GCF is 6. Dividing the numerator and denominator by the GCF, 6,

[latex]\displaystyle{\frac{54}{24} = \frac{54 ÷ 6}{24 ÷ 6} = \frac{9}{4}}[/latex]

Method 2: Prime factors of 54 are: 2 × 3 × 3 × 3. Prime factors of 24 are: 2 × 2 × 2 × 3. The common prime factors are one 2 and one 3.Therefore, [latex]\displaystyle{\frac{54}{24}}[/latex] is equal to [latex]\displaystyle{\frac{9}{4}}[/latex] reduced to its lowest terms.

Reciprocals of Fractions

Two numbers whose product equals 1 are known as reciprocals of each other. Every non-zero real number has a reciprocal.

For example,

  • [latex]\displaystyle{\frac{2}{3}}[/latex] and [latex]\displaystyle{\frac{3}{2}}[/latex] are reciprocals of each other because [latex]\displaystyle{\frac{2}{3} × \frac{3}{2} = 1}[/latex]

When the numerator and denominator of a fraction are interchanged, the resulting fraction is the reciprocal of the original fraction.

For example,

  • 5 and [latex]\displaystyle{\frac{1}{5}}[/latex] are reciprocals (5 can also be written as [latex]\displaystyle{\frac{5}{1}}[/latex]).
  • Similarly, the reciprocal of[latex]\displaystyle{\frac{-2}{5}}[/latex] is [latex]\displaystyle{\frac{5}{-2} = -\frac{5}{2}}[/latex]

The reciprocal of a positive number is always positive and the reciprocal of a negative number is always negative.

Note:

  • The reciprocal of a number is not the negative of that number. (The reciprocal of [latex]3 ≠ -3[/latex]. The reciprocal of [latex]\displaystyle{3 = \frac{1}{3}}[/latex].)
  • The reciprocal of a fraction is not an equivalent fraction of that fraction.(The reciprocal of [latex]\displaystyle{\frac{2}{5} ≠ \frac{4}{10}}[/latex]. The reciprocal of [latex]\displaystyle{\frac{2}{5} = \frac{5}{2}}[/latex].)

Table 2.3-a: Examples of Numbers with their Negatives and Reciprocals

Examples of Numbers with Their Negatives and Reciprocals
Number 5 −3 [latex]\displaystyle{\frac{2}{3}}[/latex] [latex]\displaystyle{-\frac{3}{8}}[/latex]
Negative of
the Number		 −5 3 [latex]\displaystyle{-\frac{2}{3}}[/latex] [latex]\displaystyle{\frac{3}{8}}[/latex]
Reciprocal of
the Number		 [latex]\displaystyle{\frac{1}{5}}[/latex] [latex]\displaystyle{-\frac{1}{3}}[/latex] [latex]\displaystyle{\frac{3}{2}}[/latex] [latex]\displaystyle{-\frac{8}{3}}[/latex]

2.3 Exercises

Answers to the odd-numbered problems are available at the end of the textbook.

For problems 1 to 6, classify the fractions as proper fractions, improper fractions, or mixed numbers.
  1. a. [latex]\displaystyle{\frac{16}{35}}[/latex]
    b. [latex]3\frac{2}{9}[/latex]
  2. a. [latex]15\frac{12}{13}[/latex]
    b. [latex]\displaystyle{\frac{29}{30}}[/latex]
  3. a. [latex]\displaystyle{\frac{19}{16}}[/latex]
    b. [latex]9\frac{7}{8}[/latex]
  4. a. [latex]\displaystyle{\frac{21}{22}}[/latex]
    b. [latex]\displaystyle{\frac{52}{25}}[/latex]
  5. a. [latex]4\frac{2}{5}[/latex]
    b. [latex]\displaystyle{\frac{7}{3}}[/latex]
  6. a. [latex]6\frac{1}{2}[/latex]
    b. [latex]\displaystyle{\frac{20}{75}}[/latex]
For problems 7 to 10, convert the mixed numbers to improper fractions.
  1. a. [latex]2\frac{2}{7}[/latex]
    b. [latex]3\frac{1}{8}[/latex]
  2. a. [latex]3\frac{2}{5}[/latex]
    b. [latex]7\frac{5}{8}[/latex]
  3. a. [latex]5\frac{4}{5}[/latex]
    b. [latex]6\frac{3}{4}[/latex]
  4. a. [latex]4\frac{3}{7}[/latex]
    b.[latex]9\frac{5}{6}[/latex]
For problems 11 to 14, convert the improper fractions to mixed numbers.
  1. a. [latex]\displaystyle{\frac{19}{7}}[/latex]
    b. [latex]\displaystyle{\frac{45}{8}}[/latex]
  2. a. [latex]\displaystyle{\frac{23}{7}}[/latex]
    b. [latex]\displaystyle{\frac{34}{3}}[/latex]
  3. a. [latex]\displaystyle{\frac{23}{3}}[/latex]
    b. [latex]\displaystyle{\frac{31}{6}}[/latex]
  4. a. [latex]\displaystyle{\frac{26}{4}}[/latex]
    b. [latex]\displaystyle{\frac{29}{5}}[/latex]
For problems 15 to 22, classify the pair of fractions as ‘equivalent’ or ‘not equivalent’ by first converting the mixed numbers to improper fractions.
  1. [latex]\displaystyle{\frac{44}{5}}[/latex] and [latex]4\frac{4}{5}[/latex]
  2. [latex]\displaystyle{\frac{47}{8}}[/latex] and [latex]5\frac{7}{8}[/latex]
  3. [latex]11\frac{5}{7}[/latex] and [latex]7\frac{5}{7}[/latex]
  4. [latex]\displaystyle{\frac{41}{4}}[/latex] and [latex]10\frac{3}{4}[/latex]
  5. [latex]\displaystyle{\frac{54}{7}}[/latex] and [latex]7\frac{5}{7}[/latex]
  6. [latex]\displaystyle{\frac{17}{8}}[/latex] and [latex]2\frac{3}{8}[/latex]
  7. [latex]\displaystyle{\frac{37}{9}}[/latex] and [latex]4\frac{1}{9}[/latex]
  8. [latex]\displaystyle{\frac{45}{11}}[/latex] and [latex]4\frac{3}{11}[/latex]
For problems 23 to 30, classify the pair of fractions as ‘equivalent’ or ‘not equivalent’ by first converting the improper fractions to mixed numbers.
  1. [latex]\displaystyle{\frac{15}{4}}[/latex] and [latex]3\frac{1}{4}[/latex]
  2. [latex]\displaystyle{\frac{43}{6}}[/latex] and [latex]7\frac{5}{6}[/latex]
  3. [latex]\displaystyle{\frac{18}{5}}[/latex] and [latex]3\frac{3}{5}[/latex]
  4. [latex]\displaystyle{\frac{45}{7}}[/latex] and [latex]6\frac{3}{7}[/latex]
  5. [latex]3\frac{8}{9}[/latex] and [latex]\displaystyle{\frac{35}{9}}[/latex]
  6. [latex]\displaystyle{\frac{34}{8}}[/latex] and [latex]4\frac{1}{8}[/latex]
  7. [latex]\displaystyle{\frac{41}{12}}[/latex] and [latex]3\frac{5}{12}[/latex]
  8. [latex]7\frac{3}{9}[/latex] and [latex]\displaystyle{\frac{67}{9}}[/latex]
For problems 31 to 36, (i) reduce the fractions to their lowest terms and (ii) write their reciprocals.
  1. a. [latex]\displaystyle{\frac{30}{20}}[/latex]
    b. [latex]\displaystyle{\frac{48}{84}}[/latex]
  2. a. [latex]\displaystyle{\frac{44}{12}}[/latex]
    b. [latex]\displaystyle{\frac{42}{70}}[/latex]
  3. a. [latex]\displaystyle{\frac{56}{48}}[/latex]
    b. [latex]\displaystyle{\frac{84}{21}}[/latex]
  4. a. [latex]\displaystyle{\frac{75}{105}}[/latex]
    b. [latex]\displaystyle{\frac{144}{48}}[/latex]
  5. a. [latex]\displaystyle{\frac{36}{63}}[/latex]
    b. [latex]\displaystyle{\frac{60}{96}}[/latex]
  6. a. [latex]\displaystyle{\frac{131}{84}}[/latex]
    b. [latex]\displaystyle{\frac{54}{126}}[/latex]
For problems 37 to 44, classify the pair of fractions as ‘equivalent’ or ‘not equivalent’.
  1. [latex]\displaystyle{\frac{6}{12}}[/latex] and [latex]\displaystyle{\frac{15}{30}}[/latex]
  2. [latex]\displaystyle{\frac{6}{10}}[/latex] and [latex]\displaystyle{\frac{9}{15}}[/latex]
  3. [latex]\displaystyle{\frac{8}{10}}[/latex] and [latex]\displaystyle{\frac{15}{12}}[/latex]
  4. [latex]\displaystyle{\frac{12}{18}}[/latex] and [latex]\displaystyle{\frac{18}{27}}[/latex]
  5. [latex]\displaystyle{\frac{15}{12}}[/latex] and [latex]\displaystyle{\frac{36}{45}}[/latex]
  6. [latex]\displaystyle{\frac{35}{15}}[/latex] and [latex]\displaystyle{\frac{28}{12}}[/latex]
  7. [latex]\displaystyle{\frac{20}{25}}[/latex] and [latex]\displaystyle{\frac{24}{30}}[/latex]
  8. [latex]\displaystyle{\frac{16}{24}}[/latex] and [latex]\displaystyle{\frac{25}{30}}[/latex]
For problems 45 to 50, determine the missing values.
  1. a.[latex]\displaystyle{\frac{4}{9} = \frac{?}{27}}[/latex]
    b. [latex]\displaystyle{\frac{4}{9} = \frac{20}{?}}[/latex]
  2. a.[latex]\displaystyle{\frac{42}{36} = \frac{14}{?}}[/latex]
    b. [latex]\displaystyle{\frac{42}{36} = \frac{?}{30}}[/latex]
  3. a.[latex]\displaystyle{\frac{9}{12} = \frac{18}{?}}[/latex]
    b. [latex]\displaystyle{\frac{9}{12} = \frac{?}{4}}[/latex]
  4. a.[latex]\displaystyle{\frac{45}{75} = \frac{?}{25}}[/latex]
    b. [latex]\displaystyle{\frac{45}{75} = \frac{18}{?}}[/latex]
  5. a.[latex]\displaystyle{\frac{3}{2} = \frac{12}{?}}[/latex]
    b. [latex]\displaystyle{\frac{3}{2} = \frac{?}{12}}[/latex]
  6. a.[latex]\displaystyle{\frac{25}{15} = \frac{?}{3}}[/latex]
    b. [latex]\displaystyle{\frac{25}{15} = \frac{35}{?}}[/latex]
For problems 51 to 58, express the answer as a fraction reduced to its lowest terms.
  1. What fraction of 1 year is 4 months?
  2. What fraction of 1 hour is 25 minutes?
  3. Karen cut a pizza into 16 equal slices and served 12 slices to her friends. What fraction of the pizza was served?
  4. Out of 35 students in a math class, 15 received an ‘A’ in their final exam. What fraction of the students in the class received an ‘A’ grade?
  5. In a survey of 272 people, 68 people responded ‘yes’ and the remaining responded ‘no’. What fraction of the people responded ‘no’?
  6. In a finance math course with 490 students, 70 students failed the final exam. What fraction of the students passed the final exam in this course?
  7. Out of the 480 units in a condominium tower, 182 are rented. What fraction of the units are not rented?
  8. In a community of 6,000 people, 1,800 were 60 years or older. What fraction of the people were below the age of 60 years?

Unless otherwise indicated, this chapter is an adaptation of the eTextbook Foundations of Mathematics (3rd ed.) by Thambyrajah Kugathasan, published by Vretta-Lyryx Inc., with permission. Adaptations include supplementing existing material and reordering chapters.

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Fundamentals of Business Math Copyright © 2023 by Lisa Koster and Tracey Chase is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.

Share This Book