1.5 Order of Operations

In this chapter, we have learned how to perform addition, subtraction, multiplication, division, powers, and square roots with whole numbers. In this section, we will learn the correct order (or sequence) for performing the combined arithmetic operations of whole numbers.

When there are no groupings (operations within brackets or a radical sign), the six arithmetic operations are performed in the following sequence:

  1. Exponents (Powers) and Roots
  2. Division and Multiplication, in order from left to right
  3. Addition and Subtraction, in order from left to right

Example 1.5-a: Evaluating Expressions with Mixed Arithmetic Operations

Evaluate the following arithmetic expressions:

  1. [latex]\displaystyle{16 ÷ 2^2 + 44 − 3^3}[/latex]
  2. [latex]\displaystyle{12 ÷ 3 × 2 + 5^2}[/latex]

Solution

a. [latex]\displaystyle{16 ÷ 2^2 + 44 − 3^3}[/latex]

Evaluating the exponents,

= 16 ÷ 4 + 44 − 27

Dividing,

= 4 + 44 − 27 = 48 − 27

Adding and subtracting from left to right,

= 21

b. [latex]\displaystyle{12 ÷ 3 × 2 + 5^2}[/latex]

Evaluating the exponent,

= 12 ÷ 3 × 2 + 25 = 4 × 2 + 25

Dividing and multiplying from left to right,

= 8 + 25

Adding,

= 33

When there are groupings, the arithmetic operations within the groupings are to be evaluated first. Common symbols used for groupings are brackets ( ), [ ], { }, and the radical sign
√   .

When there are groupings with more than one bracket, start by evaluating the innermost bracket, and move outwards to evaluate all expressions within the brackets by following the order of operations explained earlier.

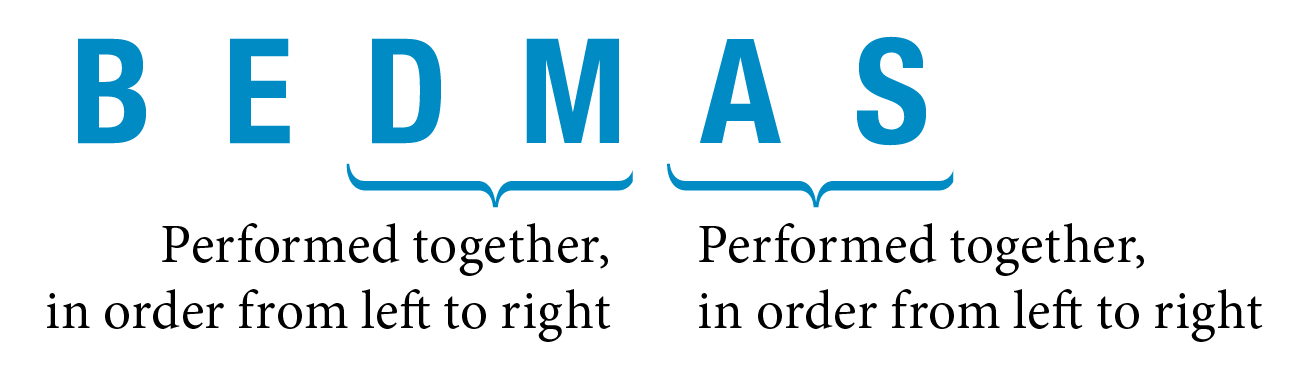
In summary, arithmetic expressions that contain multiple operations, with brackets, exponents, divisons, multiplications, additions, and subtractions, are performed in the following sequence:

  1. Brackets
  2. Exponents (Powers) and Roots
  3. Division and Multiplication, in order from left to right
  4. Addition and Subtraction, in order from left to right

The above order of operations, Brackets, Exponents, Division and Multiplication, and Addition and Subtraction, can be remembered by the following acronym:

BEDMAS acronym in blue font with DM and AS underlined. Underlined letters are performed together i order from left to right.

Example 1.5-b: Evaluating Expressions with Square Roots

Evaluate the following expressions:

  1. [latex]\displaystyle{\sqrt{49} + \sqrt{25}}[/latex]
  2. [latex]\displaystyle{\sqrt{64} - \sqrt{16}}[/latex]
  3. [latex]\displaystyle{\sqrt{4} × \sqrt{9}}[/latex]

Solution

a. [latex]\displaystyle{\sqrt{49} + \sqrt{25}}[/latex]

Evaluating the square roots,

= 7 + 5

Adding,

= 12

b. [latex]\displaystyle{\sqrt{64} - \sqrt{16}}[/latex]

Evaluating the square roots,

= 8 – 4

Subtracting,

= 4

c. [latex]\displaystyle{\sqrt{4} × \sqrt{9}}[/latex]

Evaluating the square roots,

= 2 × 3

Multiplying,

= 6

Example 1.5-c: Evaluating Expressions with Square Roots

Evaluate the following expressions:

  1. [latex]\displaystyle{5 × \sqrt{121}}[/latex]
  2. [latex]\displaystyle{\sqrt{100} ÷ 5}[/latex]
  3. [latex]\displaystyle{35 + \sqrt{49} - \sqrt{9}}[/latex]

Solution

a. [latex]\displaystyle{5 × \sqrt{121}}[/latex]

Evaluating the square root,

= 5 × 11

Multiplying,

= 55

b. [latex]\displaystyle{\sqrt{100} ÷ 5}[/latex]

Evaluating the square root,

= 10 ÷ 5

Dividing,

= 2

c. [latex]\displaystyle{35 + \sqrt{49} - \sqrt{9}}[/latex]

Evaluating the square roots,

= 35 + 7 – 3

Adding and subtracting from left to right,

= 39

Example 1.5-d: Evaluating Expressions with Groupings

Evaluate the following expressions:

  1. [latex]\displaystyle{4 × 50 ÷ (8 − 3)^2 - 1}[/latex]
  2. (100 − 3 × 24) + 8(6 − 3) ÷ 6
  3. [latex]\displaystyle{\sqrt{3^2 + 4^2} × (7 - 4) + 2}[/latex]
  4. [latex]\displaystyle{35 ÷ 7 + \sqrt{4^2 + 9}}[/latex]
  5. [latex]\displaystyle{4^2 - \sqrt{13^2 - 5^2} + 3^2\sqrt{25}}[/latex]

Solution

a. [latex]\displaystyle{4 × 50 ÷ (8 − 3)^2 - 1}[/latex]

Evaluating the operation within the bracket,

= [latex]\displaystyle{4 × 50 ÷ 5^2 - 1}[/latex]

Evaluating the exponent,

= 4 × 50 ÷ 25 − 1 = 200 ÷ 25 − 1

Dividing and multiplying from left to right,

= 8 − 1

Subtracting,

= 7

b. (100 − 3 × 24) + 8(6 − 3) ÷ 6

Evaluating the operations within the brackets in the order of operations,

= (100 – 72) + 8(3) ÷ 6

= 28 + 8(3) ÷ 6 = 28 + 24 ÷ 6

Dividing and multiplying from left to right,

= 28 + 4

Adding,

= 32

c. [latex]\displaystyle{\sqrt{3^2 + 4^2} × (7 - 4) + 2}[/latex]

Evaluating the operations within the groupings (radical sign and bracket) in the order of operations,

= [latex]\displaystyle{\sqrt{9 + 16} × 3 + 2}[/latex]

= [latex]\displaystyle{\sqrt{25} × 3 + 2}[/latex]

Evaluating the square root,

= 5 × 3 + 2

Multiplying,

= 15 + 2

Adding,

= 17

d. [latex]\displaystyle{35 ÷ 7 + \sqrt{4^2 + 9}}[/latex]

Evaluating the operations within the radical sign in the order of operations,

= [latex]\displaystyle{35 ÷ 7 + \sqrt{16 + 9}}[/latex]

= [latex]\displaystyle{35 ÷ 7 + \sqrt{25}}[/latex]

Evaluating the square root,

= 35 ÷ 7 + 5

Dividing,

= 5 + 5

Adding,

= 10

e. [latex]\displaystyle{4^2 - \sqrt{13^2 - 5^2} + 3^2\sqrt{25}}[/latex]

Evaluating the operations within the radical sign in the order of operations,

= [latex]\displaystyle{4^2 - \sqrt{169 - 25} + 3^2\sqrt{25}}[/latex]

= [latex]\displaystyle{4^2 - \sqrt{144} + 3^2\sqrt{25}}[/latex]

Evaluating the exponents and square roots,

= 16 – 12 + 9 × 5

Multiplying,

= 16 – 12 + 45 = 4 + 45

Adding and subtracting from left to right,

= 49

Example 1.5-e: Evaluating Expressions with More than One Bracket

Evaluate the following arithmetic expressions:

  1. [latex]\displaystyle{4 × 50 ÷ [(8 − 3)^2 - 5]}[/latex]
  2. [latex]\displaystyle{100 - 3 [24 ÷ 2(6 - 3)] ÷ 2}[/latex]
  3. [latex]\displaystyle{[10^2 × 4 + 50] ÷ [(8 - 3)^2 - 4^2]}[/latex]

Solution

Solutions to Example 1.5-e
Question Formulae Description
a. [latex]\displaystyle{4 × 50 ÷ [(8 − 3)^2 - 5]}[/latex] Evaluating the operation within the inner bracket,
= [latex]\displaystyle{4 × 50 ÷ [5^2 - 5]}[/latex] Evaluating the operations within the outer bracket in the order of operations,
= 4 × 50 ÷ [25 − 5]
= 4 × 50 ÷ 20 = 200 ÷ 20 Dividing and multiplying from left to right,
= 10
b. 100 − 3 [24 ÷ 2(6 − 3)] ÷ 2 Evaluating the operation within the inner bracket,
= 100 − 3[24 ÷ 2 × 3] ÷ 2 Dividing and multiplying from left to right within the outer bracket,
= 100 − 3[12 × 3] ÷ 2
= 100 − 3 × 36 ÷ 2 = 100 − 108 ÷ 2 Dividing and multiplying from left to right,
= 100 − 54 Subtracting,
= 46
c. [latex]\displaystyle{[10^2 × 4 + 50] ÷ [(8 - 3)^2 - 4^2]}[/latex]
= [latex]\displaystyle{[10^2 × 4 + 50] ÷ [5^2 - 4^2]}[/latex] Evaluating the exponents within the brackets,
= [100 × 4 + 50] ÷ [25 − 16] Dividing and multiplying from left to right within the outer bracket,
= [400 + 50] ÷ 9
= 450 ÷ 9 Dividing,
= 50

1.5 Exercises

Answers to the odd-numbered problems are available at the end of the textbook.

 

For Problems 1 to 12, evaluate the expressions with mixed arithmetic operations.
  1. a. 5 × 4 + 25 ÷ 25
    b. 64 ÷ 8 × 2
  2. a. 7 × 5 + 20 ÷ 4
    b. 36 ÷ 4 × 9
  3. a. 100 ÷ 25 × 4
    b. 18 ÷ 2 × 3 + 5
  4. a. 80 ÷ 10 × 8
    b. 50 × 2 × 5 + 10
  5. a. 32 ÷ 4 ÷ 2 × 4
    b. 96 ÷ 12 × 2 + 4
  6. a. 20 ÷ 4 × 5 + 2
    b. 56 ÷ 4 ÷ 2 × 5
  7. a. 42 × 24
    b. 32 × 23
  8. a. 52 × 23
    b. 42 × 33
  9. a. 23 + 33
    b. 52 − 42
  10. a. 52 + 62
    b. 82 − 62
  11. a. 62 × 2 − 2
    b. 100 − 52 × 3
  12. a. 52 × 3 − 15
    b. 144 − 33 × 4
For Problems 13 to 22, evaluate the expressions with square roots.
  1. a.[latex]\displaystyle{\sqrt{100} + \sqrt{25}}[/latex]
    b. [latex]\displaystyle{\sqrt{81} - \sqrt{16}}[/latex]
  2. a. [latex]\displaystyle{\sqrt{121} + \sqrt{36}}[/latex]
    b. [latex]\displaystyle{\sqrt{144} - \sqrt{9}}[/latex]
  3. a. [latex]\displaystyle{\sqrt{9} × \sqrt{16}}[/latex]
    b. [latex]\displaystyle{\sqrt{36} × \sqrt{49}}[/latex]
  4. a. [latex]\displaystyle{\sqrt{25} × \sqrt{64}}[/latex]
    b. [latex]\displaystyle{\sqrt{81} × \sqrt{121}}[/latex]
  5. a. [latex]\displaystyle{\sqrt{40} - \sqrt{24}}[/latex]
    b. [latex]\displaystyle{\sqrt{75} - \sqrt{11}}[/latex]
  6. a. [latex]\displaystyle{\sqrt{125} - \sqrt{76}}[/latex]
    b. [latex]\displaystyle{\sqrt{48} - \sqrt{23}}[/latex]
  7. a. [latex]\displaystyle{\sqrt{3^2} + \sqrt{4^2}}[/latex]
    b. [latex]\displaystyle{\sqrt{13^2} - \sqrt{5^2}}[/latex]
  8. a. [latex]\displaystyle{\sqrt{5^2} - \sqrt{4^2}}[/latex]
    b. [latex]\displaystyle{\sqrt{12^2} + \sqrt{5^2}}[/latex]
  9. a. [latex]\displaystyle{\sqrt{100 ÷ 25}}[/latex]
    b. [latex]\displaystyle{\sqrt{196 ÷ 4}}[/latex]
  10. a. [latex]\displaystyle{\sqrt{256 ÷ 4}}[/latex]
    b. [latex]\displaystyle{\sqrt{225 ÷ 25}}[/latex]
For Problems 23 to 46, evaluate the expressions with groupings.
  1. a. [latex]\displaystyle{(7 - 4)^2}[/latex]
    b. [latex]\displaystyle{(3 + 2)^3}[/latex]
  2. a. [latex]\displaystyle{(8 - 5)^3}[/latex]
    b. [latex]\displaystyle{(4 + 1)^2}[/latex]
  3. a. [latex]\displaystyle{5^2\sqrt{16} + 10 - 2}[/latex]
    b. [latex]\displaystyle{19 - 2^2\sqrt{9} + 3}[/latex]
  4. a. [latex]\displaystyle{40 - 3^2\sqrt{16} + 1}[/latex]
    b. [latex]\displaystyle{6^2\sqrt{25} + 16 - \sqrt{100}}[/latex]
  5. a. [latex]\displaystyle{(4 + 3)^2 - 5^2 + 2^3}[/latex]
    b. [latex]\displaystyle{6^2 + 2^3 - (12 - 8)^2}[/latex]
  6. a. [latex]\displaystyle{(9 - 6)^2 - 2^2 + 3^3}[/latex]
    b. [latex]\displaystyle{3^2 + 2^4 - (15 - 9)^2}[/latex]
  7. [latex]\displaystyle{12^2 - 5 × 27 ÷ (5 - 2)^2 - 3}[/latex]
  8. [latex]\displaystyle{16 ÷ 8 × 10^2 + (12 - 7)^2 × 2}[/latex]
  9. [latex]\displaystyle{3^2[(9 - 6)^2 ÷ 9 + 7 - 4]}[/latex]
  10. [latex]\displaystyle{3^2[(12^2 + 8)^2 ÷ 4 + 6 - 2]}[/latex]
  11. [latex]\displaystyle{7 + (3\sqrt{49} - 1)^2}[/latex]
  12. [latex]\displaystyle{15 + (5\sqrt{10^2} - 8)^2}[/latex]
  13. [latex]\displaystyle{16 ÷ \sqrt{64} + \sqrt{10^2 - 6^2}}[/latex]
  14. [latex]\displaystyle{\sqrt{12^2 + 5^2} - 27 ÷ \sqrt{81}}[/latex]
  15. [latex]\displaystyle{[(20 ÷ 5) × 8] ÷ (2^2 + 4)}[/latex]
  16. [latex]\displaystyle{[(6^2 ÷ 4) × 5] ÷ (2^2 + 5)}[/latex]
  17. [latex]\displaystyle{(64 ÷ 8 ÷ 4)^2 + (3^2 + 6^0)}[/latex]
  18. [latex]\displaystyle{(81 ÷ 9 ÷ 3)^2 + (9^0 + 2^2)}[/latex]
  19. [latex]\displaystyle{[(11 - 2)^2 + 3] + (16 ÷ 2)^2}[/latex]
  20. [latex]\displaystyle{(20 ÷ 2)^2 + [(13 - 6) + 4^2]}[/latex]
  21. [latex]\displaystyle{(45 - \sqrt{9^2 + 12^2}) ÷ (4^2 - \sqrt{36})}[/latex]
  22. [latex]\displaystyle{(27 + \sqrt{15^2 - 12^2}) ÷ (5^2 - \sqrt{49})}[/latex]
  23. [latex]\displaystyle{\sqrt{144} - 3^2 + (64 ÷ 4^2)^2 ÷ (18 ÷ 3^2)}[/latex]
  24. [latex]\displaystyle{\sqrt{81} + 2^2 – (36 ÷ 3^2)^2 ÷ (16 ÷ 2^2)}[/latex]

Unless otherwise indicated, this chapter is an adaptation of the eTextbook Foundations of Mathematics (3rd ed.) by Thambyrajah Kugathasan, published by Vretta-Lyryx Inc., with permission. Adaptations include supplementing existing material and reordering chapters.

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Fundamentals of Business Math Copyright © 2023 by Lisa Koster and Tracey Chase is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.

Share This Book