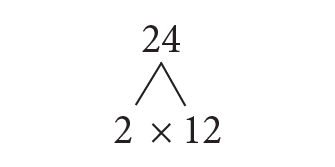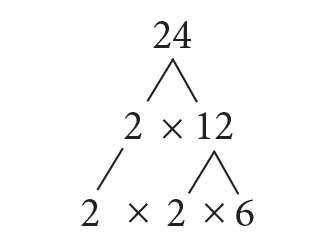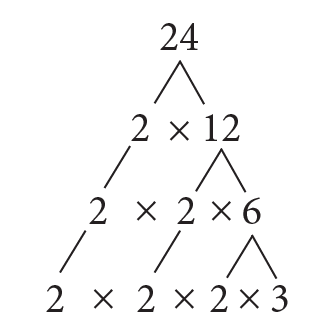1.4 Factors and Multiples
Factors of a number are whole numbers that can divide the number evenly (i.e., with no remainder).
1 is a factor of every number and every number is a factor of itself.
For example, to find factors of 12, divide the number 12 by 1, 2, 3, 4,…; the numbers that divide 12 evenly are its factors.
12 ÷ 1 = 12
12 ÷ 2 = 6
12 ÷ 3 = 4
12 ÷ 4 = 3
12 ÷ 6 = 2
12 ÷ 12 = 1
Therefore, 1, 2, 3, 4, 6, and 12 are factors of 12.
Note: 5, 7, 8, 9, 10, and 11 do not divide 12 evenly. Therefore, they are not factors of 12.
A number is divisible by another number if it divides evenly with no remainder.
We can also express the factors of a number by showing how the product of two factors results in the number.
12 = 1 × 12 or 12 × 1
12 = 2 × 6 or 6 × 2
12 = 3 × 4 or 4 × 3
Multiples of a number are the products of the number and the natural numbers (1, 2, 3, 4,…).
For example, multiples of 10:
12 = 1 × 12 or 12 × 1
12 = 2 × 6 or 6 × 2
12 = 3 × 4 or 4 × 3
Multiples of a number are the products of the number and the natural numbers (1, 2, 3, 4,…).
For example, multiples of 10:
10 × 1 = 10 10 × 2 = 20 10 × 3 = 30 10 × 4 = 40 10 × 5 = 50
Therefore, multiples of 10 are 10, 20, 30, 40, 50, etc.
Note: Multiples of a number can be divided by the number with no remainder.
Prime Numbers and Composite Numbers
A prime number is a whole number with only two factors: 1 and the number itself; i.e., prime numbers can be divided evenly only by 1 and the number itself.
For example, 7 is a prime number because it only has two factors: 1 and 7.
A composite number is a whole number with at least one factor other than 1 and the number itself; i.e., all numbers that are not prime numbers are composite numbers.
For example, 8 is a composite number because it has more than two factors: 1, 2, 4, and 8.
Note: 0 and 1 are neither prime numbers nor composite numbers.
Example 1.4-a: Identifying Prime Numbers
Identify all the prime numbers less than 25.
Solution
All the prime numbers less than 25 are:
2, 3, 5, 7, 11, 13, 17, 19, and 23.
Example 1.4-b: Identifying Composite Numbers
Identify all the composite numbers less than 25.
Solution
All the composite numbers less than 25 are:
4, 6, 8, 9, 10, 12, 14, 15, 16, 18, 20, 21, 22, and 24.
Example 1.4-c: Finding Factors of Prime Numbers
Find all the factors of 13.
Solution
1 and 13 are the only factors of 13.
Example 1.4-d: Finding All Factors of Composite Numbers
Find all the factors of:
- 16
- 20
Solution
- The factors of 16 are 1, 2, 4, 8, and 16.
- The factors of 20 are 1, 2, 4, 5, 10, and 20.
Example 1.4-e: Finding the Prime Factors of Composite Numbers
Find all the prime factors of 24.
Solution
All the factors of 24 are 1, 2, 3, 4, 6, 8, 12, and 24.
Of the above factors, only 2 and 3 are prime numbers.
Therefore, the prime factors of 24 are 2 and 3.
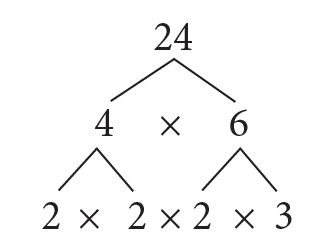
Factor Tree
A factor tree helps to find all of the prime factors of a number. It also shows the number of times each prime factor appears when writing that number as a product of its prime factors.
The following steps illustrate creating a factor tree for the number 24:
Step 2: 24 is divisible by the first prime number 2; i.e. 24 = 2 × 12.
Write these factors at the end of the two lines. Now 24 is at the top, and 2 × 12 is the 2nd layer below it, as shown.
Step 3: Now, 12 is divisible by the prime number 2, i.e. 12 = 2 × 6.
Write these factors below 12; i.e., the 3rd layer is 2 × 2 × 6, as shown.
Step 4: Next, 6 is divisible by the prime number 2; i.e. 6 = 2 × 3.
Write these factors below 6; i.e., the 4th layer is 2 × 2 × 2 × 3, as shown.
Step 5: The factors at the 4th layer are all prime numbers and cannot be factored any further.
Therefore, writing 24 as a product of its prime factors: 24 = 2 × 2 × 2 × 3.
Note: Doing every step starting with a prime number is unnecessary. You may start with two factors that multiply to get the number. For example, 24 = 4 × 6. Then continue factoring until you are left with only prime numbers on the bottom layer, as shown. The answer will be the same.
Least or Lowest Common Multiple (LCM)
The Least Common Multiple (LCM) of two or more whole numbers is the smallest multiple that is common to those numbers. LCM is the smallest integer, a common multiple of two or more numbers. The LCM can be determined using one of the following methods:
Method 1:
First, select the largest number and check to see if it is divisible by all the other numbers. If it divides, then the largest number is the LCM. For example, in finding the LCM of 2, 3, and 12, the largest number 12 is divisible by the other numbers 2 and 3. Therefore, the LCM of 2, 3, and 12 is 12.
If none of the numbers have a common factor, then the LCM of the numbers is the product of all the numbers. For example, none of these numbers have a common factor in finding the LCM of 2, 5, and 7. Therefore, the LCM of 2, 5, and 7 is 2 × 5 × 7 = 70.
If the largest number is not divisible by the other numbers and there is a common factor between some of the numbers, then find a multiple of the largest number that is divisible by all the other numbers. For example, in finding the LCM of 3, 5, and 10, the largest number 10 is not divisible by 3, and 5 and 10 have a common factor of 5. Multiples of 10 are 10, 20, 30, 40, etc. 30 are divisible by 3 and 5. Therefore, the LCM of 3, 5, and 10 is 30.
Method 2:
Step 1: Find the prime factors of each number using a factor tree and list the different prime numbers.
Step 2: Count the times each prime number appears in each factor tree.
Step 3: Find the largest of these counts for each prime number.
Step 4: List each prime number as many times as you counted it in Step 3. The LCM is the product of all the prime numbers listed.
Tip:
- A number is divisible by 2 if the last digit of the number ends in a 0, 2, 4, 6, or 8.
- A number is divisible by 3 if the sum of all the digits of a number is divisible by 3.
- A number is divisible by 5 if the last digit is 0 or 5.
Example 1.4-f: Finding the Least Common Multiple
Find the LCM of 9 and 15.
Solution
Method 1:
The largest number, 15, is not divisible by 9.
Multiples of 15 are: 15, 30, 45…
45 is divisible by 9.
Therefore, 45 is the LCM of 9 and 15.
Method 2:
Step 1 – Draw a factor tree for 9 and 15
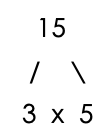
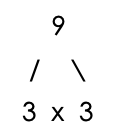
Step 2 – Count the number of times each prime number appears in the factor trees.
Number of 3’s = 2
Number of 5’s = 1
Number of 3’s = 1
Step 3 – find the largest count for each prime number.
- Largest count for the prime number 3 = 2
- Largest count for the prime number 5 = 1
Step 4 – List each prime number as many times as you counted it in Step 3.
LCM = 3x3x5 = 45
Example 1.4-g: Finding the Least Common Multiple
Find the LCM of 3, 5, and 8.
Solution
Method 1:
The largest number, 8, is not divisible by 3 and 5.
Since 3, 5, and 8 have no common factors, the LCM is the product of the three numbers:
3 × 5 × 8 = 120.
Therefore, 120 is the LCM of 3, 5, and 8.
Method 2:
Step 1 – Draw a factor tree for 3, 5 and 8
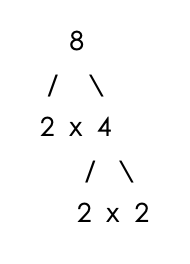
Step 2 – Count the number of times each prime number appears in the factor trees.
Number of 3’s = 1
Number of 2’s = 3
Step 3 – find the largest count for each prime number.
- Largest count for the prime number 3 = 1
- Largest count for the prime number 5 = 1
- Largest count for the prime number 2 = 3
Step 4 – List each prime number as many times as you counted it in Step 3.
LCM = 2x2x2x3x5 = 120
Find the LCM of 3, 6, and 18.
Solution
Method 1:
The largest number, 18, is divisible by both 6 and 3.
Therefore, 18 is the LCM of 3, 6, and 18.
Method 2:
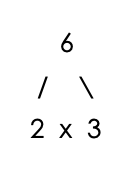
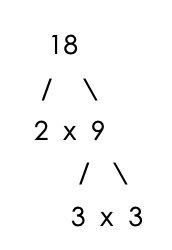
Step 2 – Count the number of times each prime number appears in the factor trees.
Number of 3’s = 1
Number of 2’s = 1
Number of 3’s = 1
Number of 2’s = 1
Number of 3’s = 2
Step 3 – find the largest count for each prime number.
- Largest count for the prime number 2 = 1
- Largest count for the prime number 3 = 2
Step 4 – List each prime number as many times as you counted it in Step 3.
LCM = 2x3x3 = 18
Example 1.4-i: Finding the Least Common Multiple
Find the LCM of 24, 36, and 48.
Solution
Method 1:
The largest number, 48, is divisible by 24 but not 36.
Multiples of 48 are 48, 96, 144,…
144 is divisible by both 24 and 36.
Therefore, 144 is the LCM of 24, 36, and 48.
Method 2:
Step 1 – Draw a factor tree for 24, 36 and 48
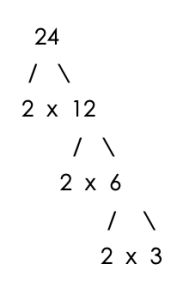
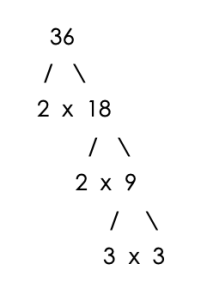
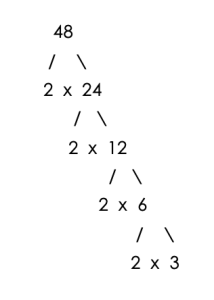
Step 2 – Count the number of times each prime number appears in the factor trees.
Number of 2’s = 3
Number of 3’s = 1
Number of 2’s = 2
Number of 3’s = 2
Number of 2’s = 4
Number of 3’s = 1
Step 3 – find the largest count for each prime number.
- Largest count for the prime number 2 = 4
- Largest count for the prime number 3 = 2
Step 4 – List each prime number as many times as you counted it in Step 3.
LCM = 2x2x2x2x3x3 = 144
Example 1.4-j: Finding the Least Common Multiple to Solve a Word Problem
Two flashing lights are turned on at the same time. One light flashes every 16 seconds, and the other flashes every 20 seconds. How often will they flash together?
Solution
In this example, we are required to find the least common interval for both lights to flash together. Both lights will continue to flash together at this interval (multiple).
Method 1:
The largest number, 20, is not divisible by 16.
Multiples of 20 are 20, 40, 60, 80,…
80 is divisble by 16.
Therefore, 80 is the LCM of 16 and 20.
Method 2:
Step 1 – Draw a factor tree for 16 and 20
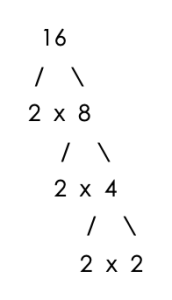
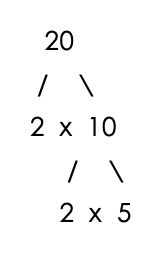
Step 2 – Count the number of times each prime number appears in the factor trees.
Number of 2’s = 4
Number of 2’s = 2
Number of 5’s = 1
Step 3 – find the largest count for each prime number.
- Largest count for the prime number 2 = 4
- Largest count for the prime number 5 = 1
Step 4 – List each prime number as many times as you counted it in Step 3.
LCM = 2x2x2x2x5 = 80
Therefore, the two flashing lights will flash together every 80 seconds.
Greatest Common Factor (GCF)
The factors that are common to two or more numbers are called common factors of those numbers.
The Greatest Common Factor (GCF) of two or more numbers is the largest common number that divides the numbers with no remainder. In other words, the GCF is the largest of all the common factors.
The GCF can be determined using one of the following methods:
Method 1:
First list all the factors of all the numbers. Then select all the common factors of the numbers. The highest value of the common factors is the GCF.
For example, in finding the GCF of 12 and 18:
- The factors of 12 are 1, 2, 3, 4, 6, and 12.
- The factors of 18 are 1, 2, 3, 6, 9, and 18.
The common factors are 2, 3, and 6.
Therefore, the GCF is 6.
Note: 1 is a factor common to all numbers, so we do not bother to include it in the list of common factors. If there are no common factors other than 1, then 1 is the greatest common factor.
For example, 1 is the only common factor of 3, 5, 7, and 9, and therefore the GCF = 1.
Method 2:
First, express each number as a product of prime factors. Then identify the set of prime factors common to all the numbers (including repetitions). The product of these prime factors is the GCF.
For example, in finding the GCF of 12 and 18:
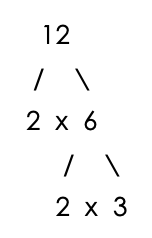
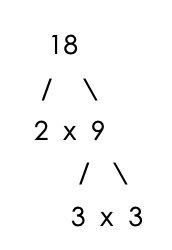
The Prime factors are:
- 12 = 2x2x3
- 18 = 2x3x3
The set of prime factors common to 12 and 18 is one 2 and one 3.
Therefore, the GCF is 2 × 3 = 6.
Example 1.4-k: Finding the Greatest Common Factor
Find the GCF of 36 and 60.
Solution
Method 1:
Factors of 36 are 1, 2, 3, 4, 6, 9, 12, 18, and 36.
Factors of 60 are 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, and 60.
The common factors are 2, 3, 4, 6, and 12.
Therefore, the GCF is 12.
Method 2:
First, express each number as a product of prime factors. Then identify the set of prime factors common to all the numbers (including repetitions). The product of these prime factors is the GCF.
For example, in finding the GCF of 36 and 60:
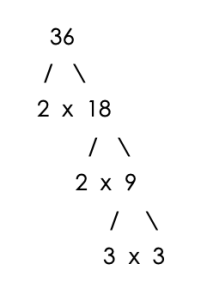
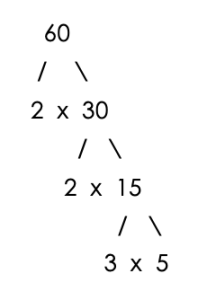
The Prime factors are:
- 36 = 2×2x3x3
- 60 = 2x2x3x5
The set of prime factors common to 36 and 60 is two 2’s and one 3.
Therefore, the GCF is 2 × 2 × 3 = 12.
Example 1.4-l: Finding the Greatest Common Factor
Find the GCF of 72, 126, and 216.
Solution
Method 1:
Factors of 72 are 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, and 72.
Factors of 126 are 1, 2, 3, 6, 7, 9, 14, 18, 21, 42, 63, and 126.
Factors of 216 are 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 27, 36, 54, 72, 108, and 216.
The common factors are 2, 3, 6, 9, and 18.
Therefore, the GCF is 18.
Method 2:
First, express each number as a product of prime factors. Then, identify the set of prime factors common to all the numbers (including repetitions). The product of these prime factors is the GCF.
For example, in finding the GCF of 72, 126 and 216
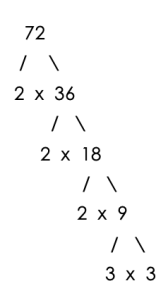
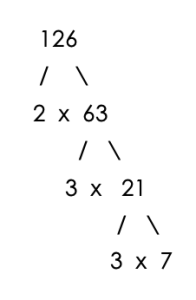
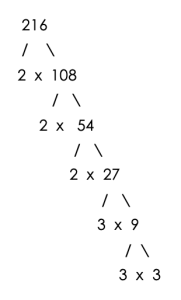
- 72=2x2x2x3×3
- 126=2x2x2x3×3
- 216=2x2x2x3x3x3
The set of prime factors which is common to 72, 126 and 216 is one 2 and two 3’s.
Therefore, the GCF is 2 × 3 x 3 = 18
Example 1.4-m: Finding the Greatest Common Factor to Solve a Word Problem
Three pieces of timber with lengths 48 cm, 72 cm, and 96 cm are to be cut into smaller pieces of equal length without remainders.
- What is the greatest possible length of each piece?
- How many pieces of such equal lengths are possible?
Solution
Method 1:
Factors of 48 are: 1, 2, 3, 4, 6, 8, 12, 16, 24, and 48.
Factors of 72 are: 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, and 72.
Factors of 96 are: 1, 2, 3, 4, 6, 8, 12, 16, 24, 32, 48, and 96.
The common factors are: 2, 3, 4, 6, 8, 12, and 24.
Therefore, the GCF is 24.
Method 2:
First, express each number as a product of prime factors. Then, identify the set of prime factors common to all the numbers (including repetitions). The product of these prime factors is the GCF.
For example, in finding the GCF of 48, 72, 96
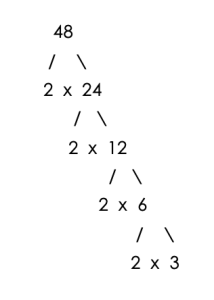
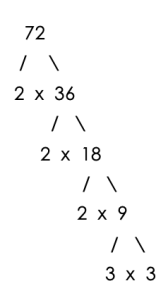
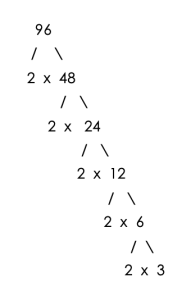
- 48=2x2x2x3
- 72=2x2x2x3x3
- 90=2x2x2x2x2x3
The set of prime factors which is common to 48, 72 and 96 is three 2’s and one 3.
Therefore, the GCF = 2 × 2 × 2 × 3 = 24.
- Therefore, the greatest possible length of each piece is 24 cm.
- The total number of equal pieces is the number of multiples of 24 cm in each piece:
48 = 24 × 2
72 = 24 × 3
96 = 24 × 4
Therefore, the total number of equal pieces of 24 cm possible is 2 + 3 + 4 = 9.
1.4 Exercises
Answers to the odd-numbered problems are available at the end of the textbook.
- List all the prime numbers less than 20.
- List all the prime numbers between 20 and 40.
- List all the composite numbers greater than 10 and less than 30.
- List all the composite numbers greater than 30 and less than 50.
- Identify the prime numbers in the given sets of numbers:
a. 13, 19, 36, 47, 49
b. 11, 14, 29, 35, 43 - Identify the prime numbers in the given sets of numbers:
a. 31, 39, 41, 59, 63
b. 23, 37, 45, 51, 53
- a. 15
b. 34 - a. 18
b. 35 - a. 64
b. 54 - a. 56
b. 60 - a. 21
b. 25 - a. 30
b. 42 - a. 36
b. 65 - a. 40
b. 49
- a. 6
b. 8 - a. 5
b. 12 - a. 9
b. 10 - a. 7
b. 15
- a. 10, 15
b. 15, 18 - a. 12, 16
b. 21, 36 - a. 18, 24
b. 35, 45 - a. 10, 25
b. 45, 60 - a. 16, 64
b. 8, 60 - a. 12, 90
b. 25, 30
- a. 2, 3, 8
b. 4, 9, 10 - a. 8, 5, 12
b. 5, 15, 20 - a. 10, 15, 25
b. 6, 27, 36 - a. 4, 8, 40
b. 3, 16, 2 - a. 14, 21, 28
b. 3, 18, 27 - a. 4, 6, 21
b. 12, 28, 42 - a. 24, 36, 12
b. 6, 15, 18 - a. 5, 12, 15
b. 12, 40, 48
- a. 15, 25
b. 18, 32 - a. 14, 35
b. 8, 36 - a. 18, 48
b. 32, 60 - a. 16, 30
b. 36, 42 - a. 25, 80
b. 40, 120 - a. 35, 75
b. 24, 64
- a. 8, 12, 15
b. 6, 15, 20 - a. 6, 8, 10
b. 10, 15, 25 - a. 12, 18, 24
b. 12, 30, 42 - a. 24, 36, 40
b. 12, 36, 48 - a. 40, 50, 80
b. 30, 75, 90 - a. 50, 75, 125
b. 60, 90, 120
- Two 96 cm and 160 cm wires are to be cut into pieces of equal length without wastage. Find the greatest possible length of each piece.
- Two ribbons 112 cm and 154 cm lengths are to be cut into pieces of equal length, without wastage. Find the greatest possible length of each piece.
- Tahrell has music lessons every 6th day and swimming lessons every 8th day. If he had music and swimming lessons on February 4th, on which date would he have both lessons again?
- Enea has skating lessons every 8th day and ballet lessons every 10th day. If she had skating and ballet lessons on March 3rd, on which date would she have both lessons again?
- Three wires measuring 18 m, 45 m, and 36 m will be cut into pieces of equal length without wastage. What is the maximum possible length of each piece?
- A store has 54 green marbles, 72 yellow marbles, and 90 red marbles. The owner packages all the marbles into bags, each containing the same number. As well, each bag has to contain marbles of the same colour. Find the maximum possible number of marbles in each bag.
- Three red, blue, and green lights flash at intervals of 15, 18, and 40 seconds, respectively. If they begin flashing at the same time, how long will it take (in minutes) until all three flashes at the same time again?
- Three bells ring simultaneously. If they ring at intervals of 24, 36, and 40 seconds, respectively, how long will it take
(in minutes) until they ring together again?
Unless otherwise indicated, this chapter is an adaptation of the eTextbook Foundations of Mathematics (3rd ed.) by Thambyrajah Kugathasan, published by Vretta-Lyryx Inc., with permission. Adaptations include supplementing existing material and reordering chapters.