1.2 Arithmetic Operations with Whole Numbers

Addition of Whole Numbers

The addition of whole numbers refers to combining two or more whole numbers to find the total.

The numbers that are added are referred to as the addends, and the result or answer is called the total or sum. The symbol ‘+’ denotes addition.

For example, 9 + 5 refers to adding 9 and 5. This is read as ‘nine plus five’.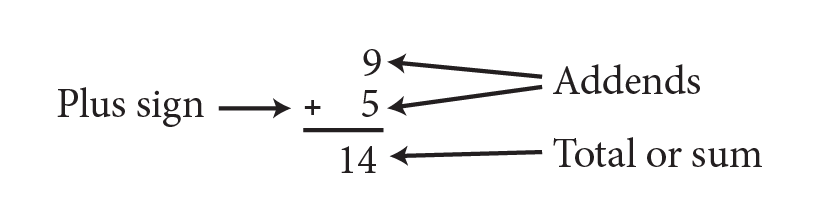Diagram of simple addition indicating the addends (9 and 5) the plus sign and the total or sum (14).Addition can be performed in any order, and the sum will be the same.

A + B = B + A

For example, 9 + 5 = 14 and 5 + 9 = 14

This is known as the cumulative property of addition.

Follow these steps to add whole numbers:

  1. Write the numbers one under the other by aligning the place values (ones, tens, hundreds,
    etc.) of the numbers and draw a horizontal line underneath.
  2. Starting from the ones place value, add all the numbers in the column.
    • If the total is less than 10, write the total under the horizontal line in the same column.
    • If the total is 10 or more, write the ‘ones’ digit under the horizontal line in the same column, and write the ‘tens’ digit above the column to the left. This is called ‘carrying’.
  3. Add the numbers in the tens column, followed by the hundreds column, etc., by following
    the same procedure for each column.

Example 1.2-a: Adding Whole Numbers

Perform the following additions:

  1. 3,514 + 245
  2. 8,578 + 3,982 + 564 + 92

Solution

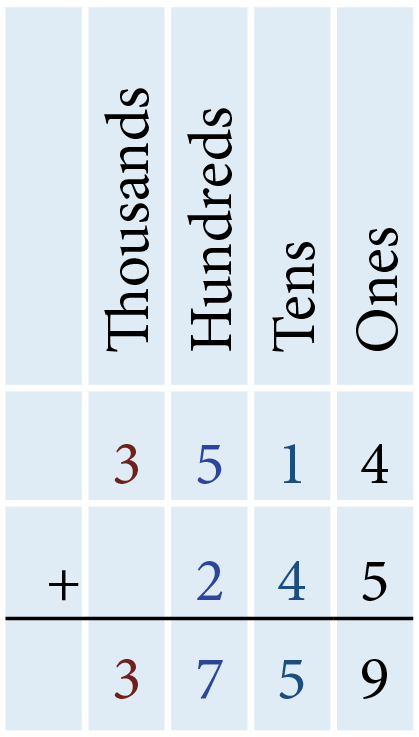
    1. 3,514 + 245
      The sum of the digits in the ones column is 9 since 4 + 5 = 9. There are 9 ones, so we write 9 in the ones column below the horizontal line. The sum of the digits in the tens column is 5 since 10 + 40 = 50. There are 5 tens, so we write 5 in the tens column below the horizontal line. The sum of the digits in the hundreds column is 7 since 500 + 200 = 700. There are 7 hundreds, so we write 7 in the hundreds column below the horizontal line. As only 3 is in the thousands column, the sum of the digits in the thousands column is 3. Write 3 in the thousands column below the horizontal line. Therefore, adding 3,514 and 245 results in 3,759.
      Adding Whole Numbers Solution a. described above.
    2. 8,578 + 3,982 + 564 + 92
      The sum of the digits in the ones column is 16 since 8 + 2 + 4 + 2 = 16, which is 1 ten and 6 ones. Write 6 in the ones column below the horizontal line and carry the 1 above the tens column. The sum of the digits in the tens column is 31 since 70 + 80 + 60 + 90 + 10 (carried from the ones column) = 310, which is 3 hundreds and 1 ten. Write 1 in the tens column below the horizontal line and carry the 3 above the hundreds column. The sum of the digits in the hundreds column is 22 since 500 + 900 + 500 + 300 (carried from the tens column) = 2,200, which is 2 thousands and 2 hundreds. Write 2 in the hundreds column below the horizontal line and carry the 2 above the thousands column. The sum of the digits in the thousands column is 13 since 8,000 + 3,000 + 2,000 (carried from the hundreds column) = 13,000, which is 1 ten thousand and 3 thousands. Write 3 in the thousands column below the horizontal line and 1 in the ten thousands column. Therefore, adding 8,578, 3,982, 564, and 92 results in 13,216.
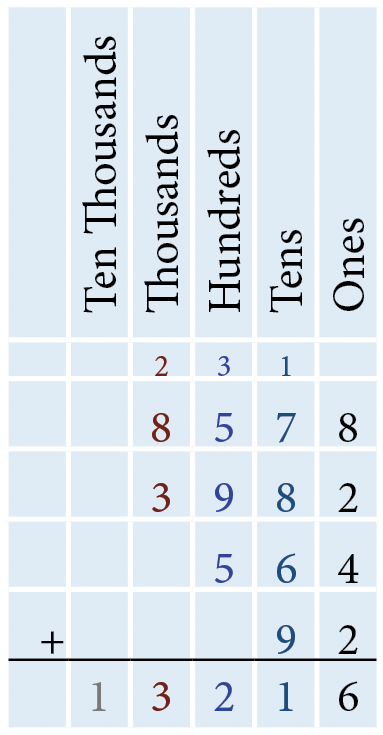
      Adding Whole Numbers Solution b. described above.

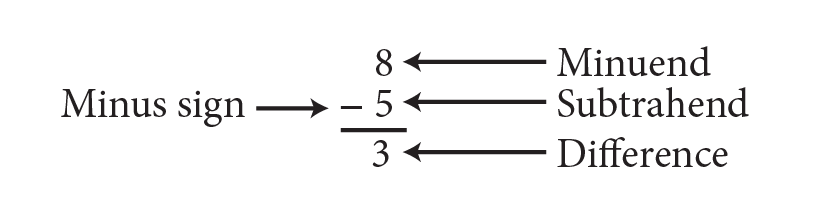
Subtraction of Whole Numbers

Subtraction of whole numbers refers to finding the difference between numbers. This is the reverse process of addition.

The number from which another number is subtracted is referred to as the minuend, and the number being subtracted is referred to as the subtrahend. The result or answer is called the difference. The symbol ‘–’ denotes subtraction.

For example, 8 – 5 refers to subtracting 5 from 8. This is read as ‘eight minus five’.

Diagram depicting a simple subtraction calculation of 8-5. 8 is the minuend, 5 is the subrahend, and three is the difference.

Subtraction must be written in the written order.

A – B does not equal B – A

For example 8 – 5 = 3 but 5 – 8 = – 3

Follow these steps to subtract a whole number from another whole number:

  1. Write the numbers one under the other by aligning the place values (ones, tens, hundreds, etc.) of the numbers and draw a horizontal line underneath. Ensure that the number being subtracted from (the minuend) is in the top row and that the number being subtracted (the subtrahend) is below.
  2. Starting from the ones place value, subtract the bottom number from the top number.
    • If the top digit is greater than (or equal to) the bottom digit, write the difference under
      the horizontal line in the same column.
    • If the top digit is less than the bottom digit, borrow ‘one’ from the digit to the left in the top number, and add ‘ten’ to the digit in the current place value of the top number. Then, find the difference and write it under the horizontal line. This is called ‘borrowing’.
  3. Subtract the numbers in the tens column, followed by the hundreds column, etc., by following the same procedure for each column.

Note: To check your answer, add the difference to the number subtracted (subtrahend); the result should be the number from which it was subtracted (minuend). e.g., 8 – 5 = 3; therefore 3 + 5 = 8

Example 1.2-b: Subtracting Whole Numbers

Perform the following subtractions:

  1. Subtract 1,314 from 3,628
  2. Subtract 789 from 8,357

Solution

  1. Subtract 1,314 from 3,628
    The difference of the digits in the ones column is 4 since 8 – 4 = 4. There are 4 ones, so we write 4 in the ones column below the horizontal line. The difference of the digits in the tens column is 1 since 20 − 10 = 10. There is 1 ten, so we write 1 in the tens column below the horizontal line. The difference of the digits in the hundreds column is 3 since 600 − 300 = 300. There are 3 hundreds, so we write 3 in the hundreds column below the horizontal line. The difference of the digits in the thousands column is 2 since 3,000 − 1,000 = 2,000. There are 2 thousands, so we write 2 in the thousands column below the horizontal line. Therefore, subtracting 1,314 from 3,628 results in 2,314.
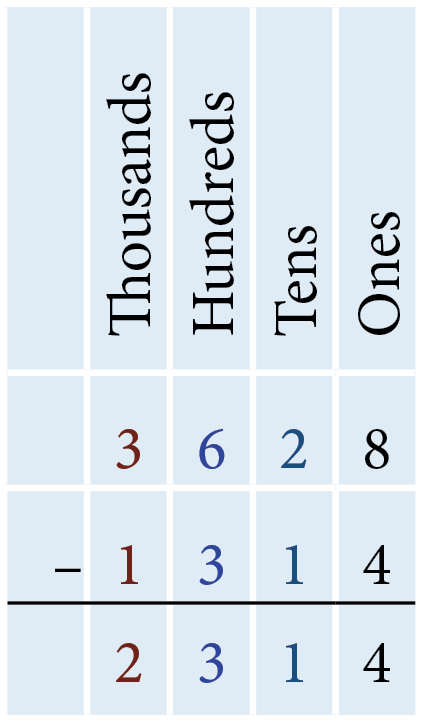
    Subtracting Whole Numbers Solution a. described above.
  2. Subtract 789 from 8,357
    In the ones column, the ones digit on the top (7) is smaller than the ones digit on the bottom (9). Borrow one ten from the tens digit on the top row and add it to the 7 ones to get 17 ones. 17 − 9 = 8, so we write 8 in the ones column below the horizontal line. In the tens column, the tens digit on the top (4, after borrowing 1 for the ones column) is smaller than the tens digit on the bottom (8). Borrow one hundred from the hundreds digit on the top row and add it to the 4 tens to get 14 tens. 14 − 8 = 6, so we write 6 in the tens column below the horizontal line.In the hundreds column, the hundreds digit on the top (2, after borrowing 1 for the tens column) is smaller than the hundreds digit on the bottom (7). Borrow one thousand from the thousands digit on the top row and add it to the 2 hundreds to get 12 hundreds. 12 − 7 = 5, so we write 5 in the hundreds column below the horizontal line. As only 7 (after borrowing 1 for the hundreds column) is in the thousands column, we write 7 in the thousands column below the horizontal line. Therefore, subtracting 789 from 8,357 results in 7,568.
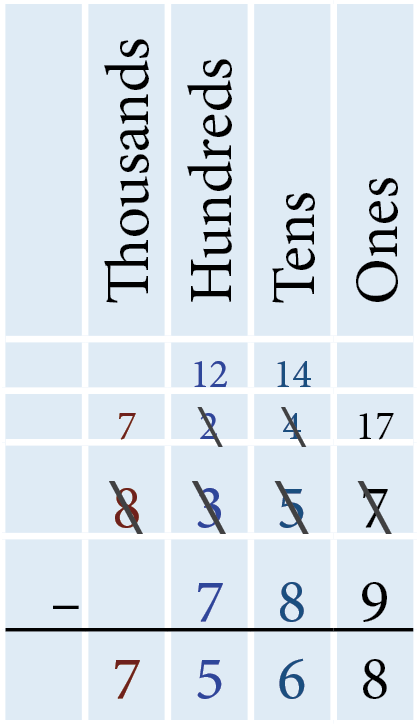
    Subtracting Whole Numbers Solution b. described above.

Note: If a larger whole number is subtracted from a smaller whole number, the result will be a negative number. To do this, reverse the question to deduct the smaller number from the larger number following the above steps, and set the answer to be negative.

Multiplication of Whole Numbers

Multiplication is the process of finding the product of two numbers. Multiplication of whole numbers can be thought of as repeated additions. The symbol ‘×’ denotes multiplication.

Multiplication can be performed in any order, and the product will be the same.

A x B = B x A

For example, 5 x 4 = 20 and 4 x 5 = 20

This is known as the commutative property of multiplication.

For example, 5 × 4 refers to repeatedly adding 5, four times. This is read as ‘five times four’, and can also be written as 5 ∙ 4 or 5(4).

5 × 4 can be represented pictorially as:

Multiplication of Whole Numbers 5 × 4. The picture shows 4 rows with 5 dots in each row.

Here, the size of the set is 5, and it is repeated 4 times:
5 + 5 + 5 + 5 = 20

This can also be viewed as 4 × 5:

Multiplication of Whole Numbers 4 × 5. The picture shows 5 columns with 4 dots in each column.

Here, the size of the set is 4, and it is repeated 5 times:
4 + 4 + 4 + 4 + 4 = 20

The numbers being multiplied are referred to as factors, and the result is the product.

Multiplication of Whole Numbers 4 × 5 (labelled as factors) and 20 as the product.

In this example, 5 and 4 are factors of 20 (the product).

Follow these steps to multiply one whole number by another whole number:

  1. Write the numbers one under the other by aligning the place values and drawing a horizontal line underneath, as done for addition and subtraction.
  2. From the ones digit of the bottom factor, multiply the digit by each digit of the top factor, starting with the right-most digit.
    • If the product is less than 10, write the product under the horizontal line.
    • If the product is 10 or more, write the ‘ones’ digit of the product under the horizontal line, carry the ‘tens’ digit, and add it to the subsequent product.
  3. Multiply the next digit of the bottom factor by each digit of the top factor by following the same procedure, and write the product below the first product, but one place value to the left. Continue for each digit of the bottom factor.
  4. Sum all the products to obtain the answer.

The above steps for multiplying numbers are provided in detail in Example 1.2-c below.

Example 1.2-c: Multiplying Whole Numbers

Perform the following multiplications:

  1. Multiply 38 by 6
  2. Multiply 36 by 24
  3. Multiply 263 by 425

Solution

  1. Multiply 38 by 6
    Multiplying 8 ones by 6 results in 48 ones. This is 4 tens and 8 ones. Write 8 in the ones column below the horizontal line and 4 above the tens column. Multiplying 3 tens by 6 results in 18 tens. Add the 4 tens from the previous step to 18 to obtain 22. Write 2 in the tens column and 2 in the hundreds column below the horizontal line. Therefore, multiplying 38 by 6 results in 228.
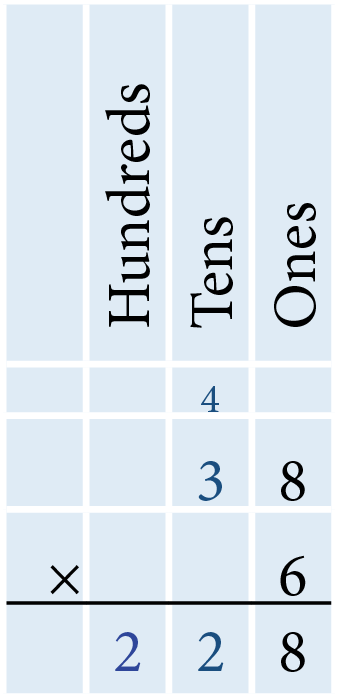
    Multiplying Whole Numbers Solution a. as described above.
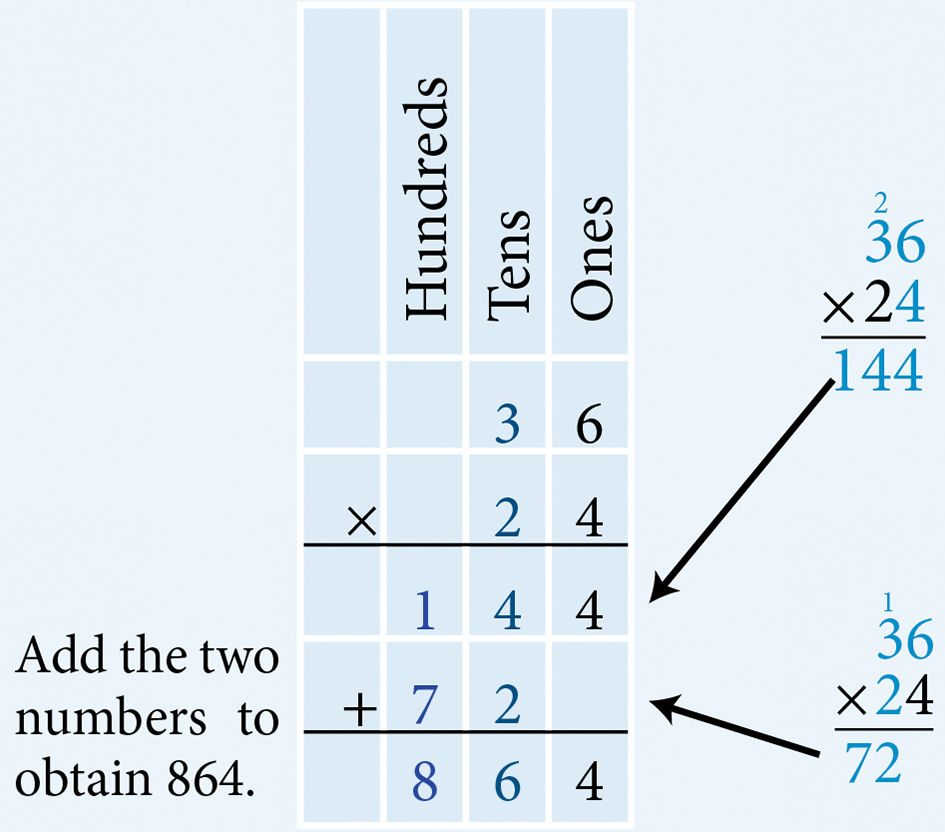
  2. Multiply 36 by 24.
    Multiply 36 by 4 ones, as shown, to obtain 144. Multiply 36 by 2 tens. To do this, write a ‘0’ under the horizontal line in the ones column (or leave it blank, as shown) and multiply 36 by 2 to obtain 72. Therefore, multiplying 36 by 24 results in 864.
    Multiplying 6 ones by 4 results in 24 ones. This is 2 tens and 4 ones. Write 4 in the ones column below the horizontal line and 2 above the tens column. Multiplying 3 tens by 4 results in 12 tens. Add the 2 tens from the previous step to 12 to obtain 14. Write 4 in the tens column and 1 in the hundreds column below the horizontal line. Write a ‘0’ under the horizontal line in the ones column (or leave it blank). Multiplying 6 ones by 2 tens results in 12. Write the 2 in the tens column below the horizontal line and 1 above the tens column. Multiplying 3 tens by 2 tens results in 6. Add the 1 ten from the previous step to 6 to obtain 7. Write 7 in the hundredths column below the 1 in the hundredths column. Add 144 and 720 together to get 864. Therefore, multiplying 36 by 24 results in 864.
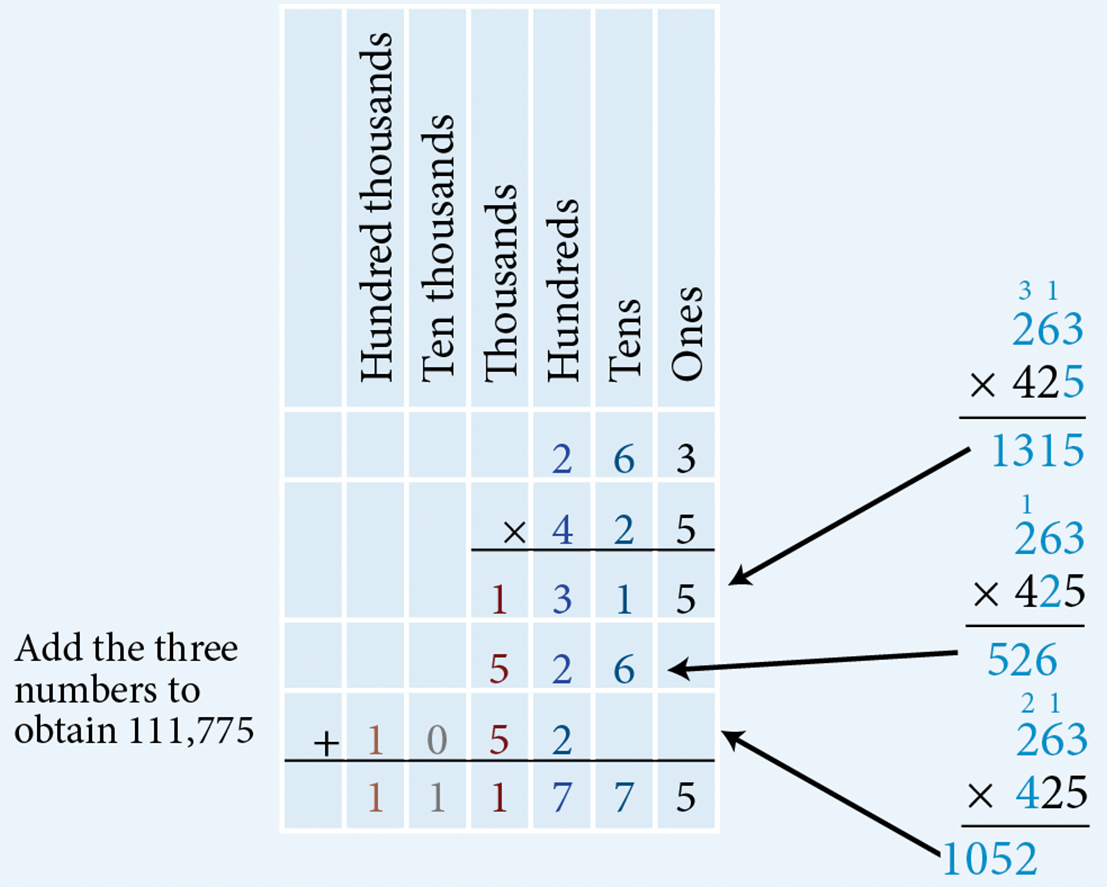
  3. Multiply 263 by 425
    Multiply 263 by 5 ones. Multiply 263 by 2 tens. Multiply 263 by 4 hundreds. Therefore, multiplying 263 by 425 results in 111,775.
    Multiplying 3 ones by 5 results in 15 ones. This is 1 ten and 5 ones. Write 5 in the ones column below the horizontal line and 1 above the tens column. Multiplying 6 by 5 results in 30. Add the 1 from the previous step to 30 to obtain 31. Write 1 in the tens column and 3 in the hundreds column above the horizontal line. Multiplying 2 by 5 ones results in 10. Add the 3 from the previous step to 10 to obtain 13. Write 1 in the thousands column and 5 in the hundreds column. Write a ‘0’ under the horizontal line in the ones column (or leave it blank). Multiplying 3 by 2 results in 6. Write 6 in the tens column under the horizontal line. Multiplying 6 by 2 results in 12. Write 2 in the hundreds column and 1 above the hundreds column. Multiplying 2 by 2 results in 4. Add 1 from the previous step to 4 to get 5. Write 5 in the thousands column. Write a ‘0’ under the horizontal line in the ones and tens column (or leave it blank). Multiplying 3 by 4 results in 12. Write 2 in the hundreds column under the horizontal line and 1 above the tens column. Multiplying 6 by 4 results in 24. Add 1 from the previous steps to 24 to get 25. Write 5 in the thousands column under the horizontal line and 2 above the hundreds column. Multiplying 2 by 4 results in 8. Add 2 from the previous step to get 10. Write 1 in the hundred thousands column and 0 in the ten thousands position. Add 1315, 5260 and 105,200 together to get 8111,775. Therefore, multiplying 263 by 425 is 111,775.

Division of Whole Numbers

The division is the process of determining how many times one number is contained in another. This is the inverse process of multiplication. When a larger number is divided by a smaller one, this division can be considered repeated subtractions. The symbol ‘÷’ denotes division.

The division must be performed in a written order.

A ÷ B does not equal B ÷ A

For example, 20 ÷ 5 = 4 but 5 ÷ 4 = [latex]\displaystyle{\frac{1}{4}}[/latex]

For example, 20 ÷ 5 refers to repeatedly subtracting 5 from 20. This is read as ‘twenty divided by five’, and can also be written as [latex]\displaystyle{\frac{20}{5}}[/latex]

 

Division of Whole Numbers 20 by 5

In a set of 20 items, we can create four groups of 5:

Division of Whole Numbers. A group of 20 is shown in 4 groups on 5.

Therefore, 20 ÷ 5 = 4.

The number being divided is referred to as the dividend, and the number by which the dividend is divided is referred to as the divisor. The result or answer is called the quotient. If the divisor cannot divide the dividend evenly, the number left over is referred to as the remainder.

For example, consider 25 ÷ 7:

Division of Whole Numbers 25 (dividend) by 7 (divisor). 3 is the quotient and 4 the remainder. 7 divides evenly into 25 3 times. 3 multiplied by 7 equals 21. The remainder is 25 - 21 = 4.

The following relationship exists between the four components of a division problem:

Dividend = Divisor × Quotient + Remainder

25 = 7 × 3 + 4

The steps to be followed in dividing whole numbers are provided in detail in Example 1.2-d below.

Example 1.2-d: Dividing Whole Numbers

Perform the following divisions and state the quotient and remainder:

  1. Divide 76 by 3
  2. Divide 637 by 25
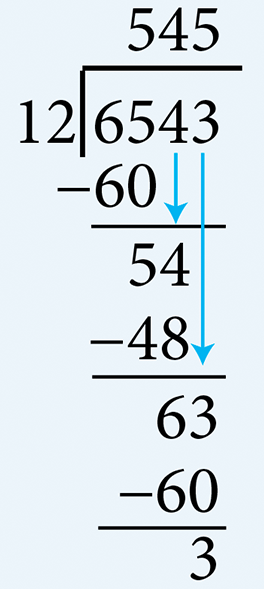
  3. Divide 6,543 by 12

Solution

  1. Divide 76 by 37 can be divided by 3. Therefore, determine the number of multiples of 3 there are in 7. There are two 3’s in 7. Write 2 in the quotient area above 7. Multiply 2 by 3 (= 6) and subtract this from 7. Write the remainder 1. Bring down the 6 from the dividend and determine the number of multiples of 3 in 16. There are five 3’s in 16. Write 5 in the quotient area above 6. Multiply 5 by 3 (= 15) and subtract this from 16 to get the final remainder of 1. Therefore, the quotient is 25 and the remainder is 1.
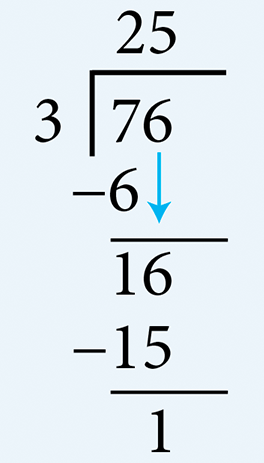
    Dividing Whole Numbers Solution a. described above.
  2. Divide 637 by 256 cannot be divided by 25. Therefore, determine the number of multiples of 25 there are in 63. There are two 25’s in 63. Write 2 in the quotient area above 3. Multiply 2 by 25 (= 50) and subtract this from 63. Write the remainder 13. Bring down the 7 from the dividend and determine the number of multiples of 25 there are in 137. There are five 25’s in 137. Write 5 in the quotient area above 7. Multiply 5 by 25 (= 125) and subtract this from 137 to get the final remainder of 12. Therefore, the quotient is 25 and the remainder is 12.
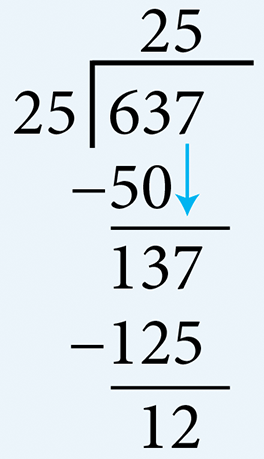
    Dividing Whole Numbers Solution b. described above.
  3. Divide 6,543 by 126 cannot be divided by 12. Therefore, determine the number of multiples of 12 there are in 65. There are five 12’s in 65. Write 5 in the quotient area above 5. Multiply 5 by 12 (= 60) and subtract this from 65. Write the remainder 5. Bring down the 4 from the dividend and determine the number of multiples of 12 there are in 54. There are four 12’s in 54. Write 4 in the quotient area above 4. Multiply 4 by 12 (= 48) and subtract this from 54. Write the remainder 6. Bring down the 3 from the dividend and determine the number of multiples of 12 there are in 63. There are five 12’s in 63. Write 5 in the quotient area above 3. Multiply 5 by 12 (= 60) and subtract this from 63 to get the final remainder of 3. Therefore, the quotient is 545 and the remainder is 3.
    Dividing Whole Numbers Solution c. described above.

Arithmetic Operations with Zero and One

Operation Description Examples
Addition When 0 is added to a number, or when a number is added to 0, there will be no change to that number. 25 + 0 = 25
0 + 25 = 25
Subtraction When 0 is subtracted from a number, there will be no change to that number. 16 – 0 = 16
When a number is subtracted from 0, the answer will be the negative value of that number. 0 – 16 = –16
Multiplication When 0 is multiplied by a number, or when a number is multiplied by 0, the answer will be 0. 0 × 35 = 0
35 × 0 = 0
Division When 0 is divided by a number, the answer will be 0. 0 ÷ 25 = 0
When a number is divided by 0, the answer is undefined. 25 ÷ 0 = Undefined
Operation Description Examples
Multiplication When 1 is multiplied by a number, or when a number is multiplied by 1, there will be no change to that number. 1 × 12 = 12
12 × 1 = 12
Division When 1 is divided by a number, the answer is the reciprocal of that number. 1 ÷ 35 = [latex]\displaystyle{\frac{1}{35}}[/latex]
When a number is divided by 1, there will be no change to that number. 1 ÷ 35 = [latex]\displaystyle{\frac{1}{35}}[/latex] = 35

Powers of Whole Numbers

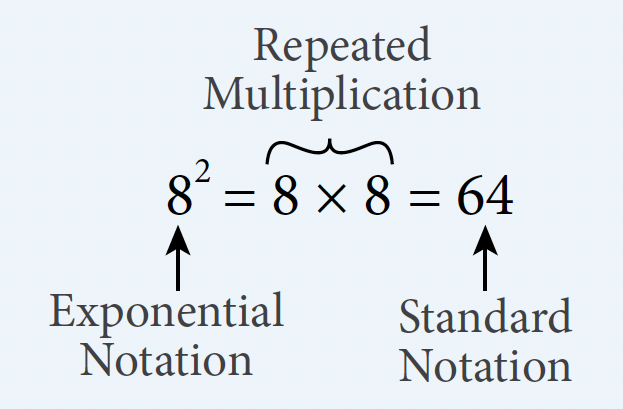
We learned previously that multiplication is a shorter way to write repeated additions of a number. Similarly, when a number is multiplied by itself repeatedly, we can represent this repeated multiplication using exponential notation.

When 2 is multiplied 5 times, in repeated multiplication, it is represented by:

2 × 2 × 2 × 2 × 2

However, it can be tedious to represent repeated multiplication using this notation. Instead, the exponential notation can be used.

When 2 is multiplied 5 times, in exponential notation, it is represented by:

Powers of Whole Numbers. 2 is the base and 5 is the exponent in this example.

In this example, 2 is known as the base, 5 is known as the exponent, and the whole representation 25 is known as the power. The exponent is written in superscript to the right of the base and represents the number of times the base is multiplied by itself. The representation is read as “2 raised to the power of 5” or “2 to the 5th power”.

Example 1.2-e: Converting Exponential Notation to Repeated Multiplication and Evaluating

Expand 82 to show the repeated multiplication and evaluate.

Solution

[latex]\displaystyle{8^2 = 8 × 8 = 64}[/latex]

Converting Exponential Notation to Repeated Multiplication and Evaluating Solution. 8 to the power of 2 is repeated multiplication of 8 x 8 which equals 64.

Example 1.2-f: Converting Repeated Multiplication to Exponential Notation

Express the repeated multiplication 9 × 9 × 9 × 9 × 9 × 9 in exponential notation.

Solution

The number 9 is being multiplied repeatedly 6 times.

In exponential notation, the base is 9 and the exponent is 6.

Therefore, 9 × 9 × 9 × 9 × 9 × 9 = [latex]\displaystyle{9^6}[/latex].

Example 1.2-g: Evaluating Expressions by Writing in Standard Form

Express the following in standard form and then evaluate:

  1. [latex]\displaystyle{5 × 3^4}[/latex]
  2. [latex]\displaystyle{2^3 × 3^2}[/latex]
  3. [latex]\displaystyle{5^4 × 2^2}[/latex]
  4. [latex]\displaystyle{5^2 × 4^2}[/latex]

Solution

  1. [latex]\displaystyle{5 × 3^4 = 5 × [ 3 × 3 × 3 × 3 ] = 5 × 81 = 405}[/latex]
  2. [latex]\displaystyle{2^3 × 3^2 = [ 2 × 2 × 2 ] × [ 3 × 3 ] = 8 × 9 = 72}[/latex]
  3. [latex]\displaystyle{5^4 × 2^2 = [ 5 × 5 × 5 × 5 ] + [ 2 × 2 ] = 625 + 4 = 629}[/latex]
  4. [latex]\displaystyle{5^2 × 4^2 = [ 5 × 5 ] – [ 4 × 4 ] = 25 – 16 = 9}[/latex]

Example 1.2-h: Evaluating Powers using a Different Power of the Same Base

Use the equation [latex]\displaystyle{6^5 = 7,776}[/latex] to evaluate the following expressions:

  1. [latex]\displaystyle{6^6}[/latex]
  2. [latex]\displaystyle{6^4}[/latex]

Solution

  1. [latex]\displaystyle{6^5 = 6 × 6 × 6 × 6 × 6 = 7,776}[/latex]
    [latex]\displaystyle{6^6 = 6 × 6 × 6 × 6 × 6 × 6}[/latex]
    [latex]\displaystyle{= 6^5 × 6}[/latex]
    [latex]\displaystyle{= 7,776 × 6}[/latex]
    [latex]\displaystyle{= 46,656}[/latex]
  2. [latex]\displaystyle{6^5 = 6 × 6 × 6 × 6 × 6 = 7,776}[/latex]
    [latex]\displaystyle{6^5 = 6^4 × 6}[/latex]
    [latex]\displaystyle{7,776 = 6^4 × 6}[/latex]
    [latex]\displaystyle{\frac{7,776}{6} = 6^4}[/latex]
    [latex]\displaystyle{6^4 = 1,296}[/latex]
Powers of 2 Powers of 3 Powers of 4 Powers of 5
[latex]\displaystyle{1^2 = 1}[/latex] [latex]\displaystyle{11^2 = 121}[/latex] [latex]\displaystyle{1^3 = 1}[/latex] [latex]\displaystyle{1^4 = 1}[/latex] [latex]\displaystyle{1^5 = 1}[/latex]
[latex]\displaystyle{2^2 = 4}[/latex] [latex]\displaystyle{12^2 = 144}[/latex] [latex]\displaystyle{2^3 = 8}[/latex] [latex]\displaystyle{2^4 = 16}[/latex] [latex]\displaystyle{2^5 = 32}[/latex]
[latex]\displaystyle{3^2 = 9}[/latex] [latex]\displaystyle{13^2 = 169}[/latex] [latex]\displaystyle{3^3 = 27}[/latex] [latex]\displaystyle{3^4 = 81}[/latex] [latex]\displaystyle{3^5 = 243}[/latex]
[latex]\displaystyle{4^2 = 16}[/latex] [latex]\displaystyle{14^2 = 196}[/latex] [latex]\displaystyle{4^3 = 64}[/latex] [latex]\displaystyle{4^4 = 256}[/latex] [latex]\displaystyle{4^5 = 1,024}[/latex]
[latex]\displaystyle{5^2 = 25}[/latex] [latex]\displaystyle{15^2 = 225}[/latex] [latex]\displaystyle{5^3 = 125}[/latex] [latex]\displaystyle{5^4 = 625}[/latex] [latex]\displaystyle{5^5 = 3,125}[/latex]
[latex]\displaystyle{6^2 = 36}[/latex] [latex]\displaystyle{16^2 = 256}[/latex] [latex]\displaystyle{6^3 = 216}[/latex] [latex]\displaystyle{6^4 = 1,296}[/latex] [latex]\displaystyle{6^5 = 7,776}[/latex]
[latex]\displaystyle{7^2 = 49}[/latex] [latex]\displaystyle{17^2 = 289}[/latex] [latex]\displaystyle{7^3 = 343}[/latex] [latex]\displaystyle{7^4 = 2,401}[/latex] [latex]\displaystyle{7^5 = 16,807}[/latex]
[latex]\displaystyle{8^2 = 64}[/latex] [latex]\displaystyle{18^2 = 324}[/latex] [latex]\displaystyle{8^3 = 512}[/latex] [latex]\displaystyle{8^4 = 4,096}[/latex] [latex]\displaystyle{8^5 = 32,768}[/latex]
[latex]\displaystyle{9^2 = 81}[/latex] [latex]\displaystyle{19^2 = 361}[/latex] [latex]\displaystyle{9^3 = 729}[/latex] [latex]\displaystyle{9^4 = 6,561}[/latex] [latex]\displaystyle{9^5 = 59,049}[/latex]
[latex]\displaystyle{10^2 = 100}[/latex] [latex]\displaystyle{20^2 = 400}[/latex] [latex]\displaystyle{10^3 = 1,000}[/latex] [latex]\displaystyle{10^4 = 10,000}[/latex] [latex]\displaystyle{10^5 = 100,000}[/latex]

Perfect Squares and Square Roots

Any whole number base with an exponent of 2 is a perfect square. For example, 9 is the perfect square produced by 3 raised to an exponent 2. The first twenty perfect squares are shown in Table 1.2-c under Powers of 2.

Finding the square root of a perfect square is the inverse of raising a whole number to the power of 2. The square root of a number is one of two identical factors that, when multiplied together, results in that number.

For example,

  • 2 is the square root of 4 because [latex]\displaystyle{2^2 = 4}[/latex] or [latex]\displaystyle{2 × 2 = 4}[/latex]
  • 5 is the square root of 25 because [latex]\displaystyle{5^2 = 25}[/latex] or [latex]\displaystyle{5 × 5 = 25}[/latex]

A whole number multiplied by itself results in a perfect square. The whole number multiplied by itself to get that perfect square is called the square root of that perfect square.

For example,

  • 16 is a perfect square because it is the product of two identical factors of 4; i.e., 16 = 4 × 4.
  • Therefore, 4 is the square root of 16.

The radical sign [latex]\displaystyle{\sqrt{ }}[/latex] indicates the root of a number (or expression). The square root of 16, using the radical sign, is represented by [latex]\displaystyle{\sqrt[2]{16}}[/latex], where 2 is the index. The index indicates which root is to be taken, and is written as a small superscript number to the left of the radical symbol. For square roots, the index 2 does not need to be written as it is understood to be there; i.e. [latex]\displaystyle{\sqrt[2]{16}}[/latex] is written as [latex]\displaystyle{\sqrt{16}}[/latex].

Note: In future chapters, we will discuss roots with indexes other than 2.

Example 1.2-i: Determining the Square Root of Perfect Squares

Determine the square root of the following:

  1. [latex]\displaystyle{\sqrt{36}}[/latex]
  2. [latex]\displaystyle{\sqrt{81}}[/latex]
  3. [latex]\displaystyle{\sqrt{144}}[/latex]

Solution

  1. [latex]\displaystyle{\sqrt{36} = \sqrt{6 × 6} = 6}[/latex](Using 36 = 6 × 6)
  2. [latex]\displaystyle{\sqrt{81} = \sqrt{9 × 9} = 9}[/latex](Using 81 = 9 × 9)
  3. [latex]\displaystyle{\sqrt{36} = \sqrt{12 × 12} = 12}[/latex](Using 144 = 12 × 12)

1.2 Exercises

Answers to the odd-numbered problems are available at the end of the textbook.

 

For addition Problems 1 to 8, (i) estimate the answer by rounding each number to the nearest ten and (ii) calculate the exact answer.
  1. a. 48 + 29
    b. 38 + 95
  2. a. 16 + 79
    b. 69 + 47
  3. a. 875 + 48
    b. 574 + 79
  4. a. 459 + 27
    b. 356 + 65
  5. a. 286 + 109 + 15
    b. 839 + 645 + 27
  6. a. 989 + 215 + 25
    b. 798 + 237 +12
  7. a. 195 + 459 + 8
    b. 996 + 816 + 6
  8. a. 896 + 642 + 9
    b. 995 + 724 + 8
For the addition Problems 9 to 14, estimate the answer by (i) rounding each number to the nearest hundred, and (ii) calculate the exact answer.
  1. a. 745 + 668
    b. 427 + 225
  2. a. 357 + 245
    b. 451 + 645
  3. a. 1,883 + 5,466
    b. 2,157 + 3,459
  4. a. 6,950 + 2,367
    b. 3,765 + 1,992
  5. a. 2,635 + 372 + 1,524
    b. 653 + 2,188 + 891
  6. a. 1,650 + 1,647 + 875 + 167
    b. 3,869 + 1,967 + 550 + 745
For the subtraction Problems 15 to 22, (i) estimate the answer by rounding each number to the nearest ten, and (ii) calculate the exact answer.
  1. a. 62 − 25
    b. 33 – 18
  2. a. 43 − 27
    b. 71 − 59
  3. a. 208 − 79
    b. 315 − 47
  4. a. 327 − 28
    b. 500 − 73
  5. a. 767 − 159
    b. 804 − 308
  6. a. 904 − 629
    b. 584 − 167
  7. a. 8,302 − 7,244
    b. 2,927 − 888
  8. a. 9,185 − 6,728
    b. 5,765 − 777
For subtraction Problems 23 to 28, (i) estimate the answer by rounding each number to the nearest hundred, and (ii) calculate the exact answer.
  1. a. 946 – 452
    b. 855 – 251
  2. a. 868 – 74
    b. 495 – 357
  3. a. 2,950 – 2,275
    b. 3,961 – 1,833
  4. a. 2,955 – 1,350
    b. 1,967 – 352
  5. a. 3,513 – 2,846
    b. 3,981 – 1,657
  6. a. 7,676 – 3,969
    b. 5,789 – 5,626
For the multiplication Problems 29 to 34, (i) estimate the answer by rounding each number to the nearest ten, and (ii) calculate the exact answer.
  1. a. 58 × 75
    b. 63 × 59
  2. a. 35 × 97
    b. 95 × 71
  3. a. 764 × 53
    b. 799 × 68
  4. a. 482 × 95
    b. 755 × 55
  5. a. 1,995 × 37
    b. 2,150 × 59
  6. a. 2,996 × 32
    b. 2,995 × 38
For the division Problems 35 to 44, (i) estimate the answer by rounding each number to the nearest ten, and (ii) perform the exact division and state the quotient and the remainder.
  1. a. 78 ÷ 5
    b. 36 ÷ 8
  2. a. 69 ÷ 7
    b. 85 ÷ 9
  3. a. 86 ÷ 27
    b. 78 ÷ 19
  4. a. 59 ÷ 12
    b. 95 ÷ 18
  5. a. 654 ÷ 14
    b. 396 ÷ 24
  6. a. 777 ÷ 16
    b. 255 ÷ 19
  7. a. 2,562 ÷ 18
    b. 1,225 ÷ 28
  8. a. 2,097 ÷ 55
    b. 1,795 ÷ 64
  9. a. 3,004 ÷ 204
    b. 6,501 ÷ 498
  10. a. 3,895 ÷ 264
    b. 5,195 ÷ 255
For Problems 45 to 48, express the repeated multiplication in exponential notation.
  1. a. 6 × 6 × 6 × 6
    b. 12 × 12
  2. a. 5 × 5 × 5
    b. 7 × 7 × 7 × 7 × 7
  3. a. 3 × 3 × 3 × 3 × 3 × 3
    b. 9 × 9 × 9 × 9
  4. a. 8 × 8 × 8 × 8 × 8
    b. 4 × 4 × 4 × 4 × 4
For Problems 49 to 52, write the base and exponent for the powers.
  1. a. [latex]\displaystyle{2^9}[/latex]
    b. [latex]\displaystyle{5^7}[/latex]
  2. a. [latex]\displaystyle{6^2}[/latex]
    b. [latex]\displaystyle{10^9}[/latex]
  3. a. [latex]\displaystyle{1^{20}}[/latex]
    b. [latex]\displaystyle{8^3}[/latex]
  4. a. [latex]\displaystyle{7^{5}}[/latex]
    b. [latex]\displaystyle{12^1}[/latex]
For Problems 53 and 54, express the powers in standard notation and then evaluate.
  1. a. [latex]\displaystyle{10^6}[/latex]
    b. [latex]\displaystyle{3^5}[/latex]
  2. a. [latex]\displaystyle{2^8}[/latex]
    b. [latex]\displaystyle{5^4}[/latex]
  1. If [latex]\displaystyle{3^{10} = 59,049}[/latex], evaluate a) [latex]\displaystyle{3^9}[/latex] and b) [latex]\displaystyle{3^{11}}[/latex]
  2. If [latex]\displaystyle{5^8 = 390,625}[/latex], evaluate a) [latex]\displaystyle{5^7}[/latex] and b) [latex]\displaystyle{5^9}[/latex]
For Problems 57 to 62, determine the square root.
  1. a. [latex]\displaystyle{\sqrt{64}}[/latex]
    b. [latex]\displaystyle{\sqrt{121}}[/latex]
  2. a. [latex]\displaystyle{\sqrt{25}}[/latex]
    b. [latex]\displaystyle{\sqrt{225}}[/latex]
  3. a. [latex]\displaystyle{\sqrt{1}}[/latex]
    b. [latex]\displaystyle{\sqrt{324}}[/latex]
  4. a. [latex]\displaystyle{\sqrt{100}}[/latex]
    b. [latex]\displaystyle{\sqrt{400}}[/latex]
  5. a. [latex]\displaystyle{\sqrt{8^2}}[/latex]
    b. [latex]\displaystyle{\sqrt{20^2}}[/latex]
  6. a. [latex]\displaystyle{\sqrt{12^2}}[/latex]
    b. [latex]\displaystyle{\sqrt{45^2}}[/latex]
  1. a. What amount is $65 less than $784?
    b. What amount is $35 more than $98?
  2. a. What amount is $79 less than $487?
    b. What amount is $97 more than $52?
  3. a. What amount is $515 increased by $847?
    b. What amount is $745 decreased by $125?
  4. a. What amount is $745 increased by $1,274?
    b. What amount is $526 decreased by $346?
  5. a. If there are 24 pens in a box, how many pens are there in 15 boxes?
    b. A wire of length 420 centimetres is to be cut into 35-centimetre pieces. How many 35-centimetre pieces can be cut?
  6. a. If you save $125 every month, how much will you save in one year?
    b. If 8 people can be seated at a dinner table, how many tables are required to seat 280 people?
  7. a. If you save $15 a week, how many weeks will it take you to save $675?
    b. If there are 16 chairs in a row, how many chairs are there in 22 rows?
  8. a. If you work 25 hours per week, how many weeks will it take you to complete a job that requires 450 hours?
    b. If you earn $18 per hour, how much will you earn in a week in which you have worked 32 hours?
  9. Mythili went to a bookstore and bought a dictionary. She gave the cashier a $100 note and received $47 as change. How much did the dictionary cost?
  10. There were 744 students in a primary school. In May, after some students left to join another school, 576 students remained. How many students left for the other school?
  11. Andy has $1,238 and Bill has $346 less than Andy. How much money do both of them have together?
  12. A television costs $649 more than a Blu-ray player. If the Blu-ray player costs $235, how much will it cost to buy the TV and the Blu-ray player?
  13. Peter earns $18 per hour. If he worked 25 hours last week, calculate his earning for that week.
  14. Sam’s overtime rate is $37 per hour. If he worked 29 hours overtime last week, calculate his overtime pay for that week.
  15. Earl wants to save $3,150. If he saves $75 per week, how many weeks will it take for him to achieve his goal?
  16. How long will it take to travel 1,190 km at 85 km per hour?
  17. A large group of students visited an exhibition on Friday. The first 275 students were given one free balloon each. 487 students were disappointed that they did not receive any balloons. How many students visited the exhibition?
  18. There were 2,415 boys and 1,875 girls that attended a fair. The first 2,650 visitors to the fair received gifts. How many visitors did not receive gifts?
  19. There were 450 passengers on a train. Half of them were men, 125 were children, and the rest were women. How many more men than women were there on the train?
  20. Out of the 3,678 visitors at an art exhibition, 1,469 were men, 1,234 were women, and the rest were children. How many more adults than children went to the exhibition?
  21. Aran had some money saved up. On his birthday, Aran’s grandparents gave him $125. After spending $98 on toys and $75 on clothes, he had $115 remaining. What amount did Aran have in his savings before his birthday?
  22. Girija had some biscuits. She ate 19 and gave 27 to her brother and 5 to her parents. She had 12 biscuits left. How many biscuits did Girija have originally?
  23. There are 19 girls in a class of 43 students. 15 of the girls and 11 of the boys are wearing eyeglasses.
    a. How many boys are there in the class?
    b. How many students do not wear eyeglasses?
  24. There are 22 players on a soccer field. 10 players are wearing blue and 2 are wearing green. The rest of the players are wearing red. How many players are wearing red?

Unless otherwise indicated, this chapter is an adaptation of the eTextbook Foundations of Mathematics (3rd ed.) by Thambyrajah Kugathasan, published by Vretta-Lyryx Inc., with permission. Adaptations include supplementing existing material and reordering chapters.

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Fundamentals of Business Math Copyright © 2023 by Lisa Koster and Tracey Chase is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.

Share This Book