1.3 Arithmetic Operations with Signed Numbers
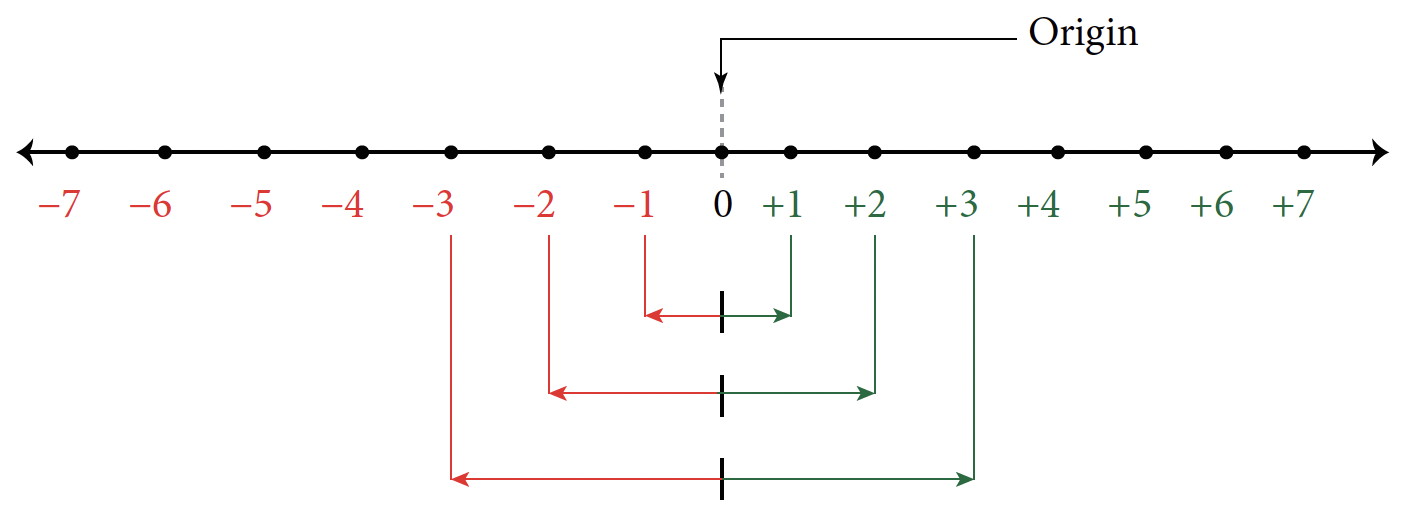
Positive real numbers can be represented by points on a number line from zero to the right of the zero. That is, whole numbers and positive rational and irrational numbers can be represented on a number line from zero to the right of zero.
Every positive number has a negative number known as its opposite, which lies to the left of zero on the number line. We use the negative sign '−' to represent negative numbers and the positive sign '+' to represent positive numbers. Zero, '0', is neither positive nor negative.
For example, plotting the positive numbers [latex]\displaystyle{\frac{3}{4}}[/latex], 4, and 6.5 and their opposites on the number line:
The arrowhead on either end shows that the number line continues indefinitely in both the positive and negative directions.
Positive and negative numbers are collectively called signed numbers. Since numbers are naturally positive, we usually omit the word ‘positive’ or the positive sign (+) when we read or write positive numbers. However, we must read or write the number as ‘negative’ or include the negative sign (−) when the number is negative. For example, ‘+7’ is read as ‘seven’ and written as ‘7’. However, ‘−7’ is read as ‘negative seven’ and written with the negative sign as ‘−7’.
Any positive number and its negative (opposite) will equal zero (origin) on the number line.
Numbers that lie to the left of a number on the number line are less than that number, and those that lie to the right on a number line are greater than that number.
For example,
- 3 is greater than −2, i.e., 3 > –2
- −3 is greater than −5, i.e., –3 > –5
- −5 is less than −4, i.e., –5 < –4
- −1 is less than 2, i.e., –1 < 2
Addition and Subtraction of Signed Numbers
- The answer is always positive (+) when adding two positive numbers. For example, Adding +5 and +3: (+5) + (+3) = 5 + 3 = 8. This is the same as +8.

- The answer is always negative when adding two negative numbers (−). For example,Adding −4 and −3: (−4) + (−3) = −4 − 3 = −7

- When adding numbers with different signs, subtract the smaller absolute value (positive value) from, the larger absolute value (positive value), and keep the sign of the number with the larger absolute value. For example,
- When subtracting negative numbers, change all the subtraction problems to addition problems by adding the opposite, and then follow the rules for adding signed numbers. For example,
- Subtracting 12 from 18:18 – 12 = 18 + (–12) = 6
- Subtracting –12 from 18:18 – (–12) = 18 + 12 = 30
- Subtracting 12 from –18:–18 – 12 = –18 + (–12) = –30
- Subtracting –12 from –18:–18 – (–12) = –18 + 12 = –6
Multiplication and Division of Signed Numbers
When multiplying two signed numbers:
- The product of two numbers with the same sign is positive. For example,
- (+5)(+4) = +20
- (–5)(–4) = +20
- The product of two numbers with different signs is negative. For example,
- (+5)(−4) = −20
- (−5)(+4) = −20
When dividing two signed numbers:
- The quotient of two numbers with the same sign is positive. For example,
- [latex]\displaystyle{\frac{+12}{+8} = \frac{3}{2}}[/latex]
- [latex]\displaystyle{\frac{-12}{-8} = \frac{3}{2}}[/latex]
- The quotient of two numbers with different signs is negative. For example,
- [latex]\displaystyle{\frac{-12}{+8} = -\frac{3}{2}}[/latex]
- [latex]\displaystyle{\frac{+12}{-8} = -\frac{3}{2}}[/latex]
When multiplying or dividing more than two signed numbers, group them into pairs to determine the sign using the rules for multiplication and division of signed numbers.
For example,
- [latex](-3)(-2)(+4)(-1)(-5) = (6)(-4)(-5)[/latex][latex]= (-24)(-5) = 120[/latex]
- [latex]\displaystyle{\frac{(-15)(+8)(-50)}{(-25)(14)} = \frac{-(15 \times 8)(-50)}{-(25 \times 14)} = \frac{+(15 \times 8 \times 50)}{-(25 \times 14)}}[/latex][latex]\displaystyle{= \frac{+(15 \times 4 \times 2)}{-(1 \times 7)} = -\frac{15 \times 4 \times 2}{7} = -\frac{120}{7}}[/latex]
Powers with Negative Bases
When a power has a negative base, there are four possible scenarios, as outlined in the following table:
Table 1.3-a: Powers with Negative Bases
| Sign and Parity of Exponent |
Example | Sign of Answer |
|---|---|---|
| Positive and Even |
[latex](-2)^6 = (-2)(-2)(-2)(-2)(-2)(-2) = 64[/latex] | + |
| Positive and Odd |
[latex](-2)^5 = (-2)(-2)(-2)(-2)(-2) = -32[/latex] | − |
| Negative and Even |
[latex]\displaystyle{(-2)^{-6} = \frac{1}{(-2)^6} = \frac{1}{(-2)(-2)(-2)(-2)(-2)(-2)} = \frac{1}{64} = 0.015625}[/latex] | + |
| Negative and Odd |
[latex]\displaystyle{(-2)^{-5} = \frac{1}{(-2)^5} = \frac{1}{(-2)(-2)(-2)(-2)(-2)} = \frac{1}{-32} = -0.03125}[/latex] | − |
From the above scenarios, you will note:
- A negative base with an even exponent produces a positive result (because pairs of negatives become positive).
- A negative base with an odd exponent produces a negative result (because after negatives are paired, one negative will be left over).
A negative base of a power expressed within a bracket, as in [latex](-a)^n[/latex], results in a different answer than a negative base expressed without a bracket, as in [latex]-a^n[/latex].
In [latex](-a)^n[/latex], the exponent applies to both the negative sign and [latex]a[/latex].
In [latex]-a^n[/latex], the exponent applies only to [latex]a[/latex] and the negative sign is applied to the answer.
For example,
- In [latex](-5)^4[/latex], [latex](-5)[/latex] is multiplied [latex]4[/latex] times; i.e., [latex](-5)^4 = (-5)(-5)(-5)(-5) = 625[/latex]
- In [latex](-5)^3[/latex], [latex](-5)[/latex] is multiplied [latex]3[/latex] times; i.e., [latex](-5)^3 = (-5)(-5)(-5) = -125[/latex]
- In [latex]-5^4[/latex], only [latex]5[/latex] is multiplied [latex]4[/latex] times and the answer is negative; i.e., [latex]-5^4 = -[5 \times 5 \times 5 \times 5] = -625[/latex]
- In [latex]-5^3[/latex], only [latex]5[/latex] is multiplied [latex]3[/latex] times and the answer is negative; i.e., [latex]-5^3 = -[5 \times 5 \times 5] = -125[/latex]
Example 1.3-a: Evaluating Expressions with Negative Bases using the Product Rule
Evaluate the following expressions:
- [latex](-5)^4 \times (-5)^{-1}[/latex]
- [latex](-2)^5 \times (-2)^2 \times (-2)^0 \times 2[/latex]
Solution
- [latex](-5)^4 \times (-5)^{-1} = (-5)^{(4 - 1)} = (-5)^3 = -125[/latex]
- [latex](-2)^5 \times (-2)^2 \times (-2)^0 \times 2 = (-2)^{(5 + 2 + 0)} \times 2[/latex][latex]= (-2)^7 \times 2 = -128 \times 2 = -256[/latex]
Example 1.3-b: Evaluating Expressions with Negative Bases using the Quotient Rule
Evaluate the following expressions:
- [latex](-3)^7 \div (-3)^2[/latex]
- [latex](-5)^3 \div (-5)^0[/latex]
Solution
- [latex](-3)^7 \div (-3)^2 = (-3)^{(7 - 2)} = (-3)^5 = -243[/latex]
- [latex](-5)^3 \div (-5)^0 = (-5)^{(3 - 0)} = (-5)^3 = -125[/latex]
Example 1.3-c: Evaluating Expressions with Negative Bases using the Power of a Product Rule
Evaluate the following expressions:
- [latex](-5 \times 2)^3[/latex]
- [latex](-3 \times 2)^{-2}[/latex]
Solution
- [latex](-5 \times 2)^3 = (-5)^3 \times 2^3 = -125 \times 8 = -1,000[/latex]or[latex](-5 \times 2)^3 = (-10)^3 = -1,000[/latex]
- [latex]\displaystyle{(-3 \times 2)^{-2} = (-3)^{-2} \times 2^{-2} = \frac{1}{(-3)^2} \times \frac{1}{2^2} = \frac{1}{9} \times \frac{1}{4} = \frac{1}{36}}[/latex]or[latex]\displaystyle{(-3 \times 2)^{-2} = (-6)^{-2} = \frac{1}{(-6)^2} = \frac{1}{36}}[/latex]
Example 1.3-d: Evaluating Expressions with Negative Bases using the Power of a Quotient Rule
Evaluate the following expressions:
- [latex](-2 \div 3)^{-2}[/latex]
- [latex](3 \div (-2))^{-3}[/latex]
Solution
- [latex]\displaystyle{(-2 \div 3)^{-2} = \left(\frac{-2}{3}\right)^{-2} = \left(\frac{3}{-2}\right)^2 = \frac{3^2}{(-2)^2} = \frac{9}{4}}[/latex]
- [latex]\displaystyle{(3 \div (-2))^{-3} = \left(\frac{3}{-2}\right)^{-3} = \left(\frac{-2}{3}\right)^3 = \frac{(-2)^3}{3^3} = \frac{-8}{27} = -\frac{8}{27}}[/latex]
Example 1.3-e: Evaluating Expressions with Negative Bases using the Power of a Power Rule
Evaluate the following expressions:
- [latex](-2^3)^3[/latex]
- [latex](-3^3)^2[/latex]
Solution
- [latex](-2^3)^3 = (-2)^{3 \times 3} = (-2)^9 = -512[/latex]
- [latex](-3^3)^2 = (-3)^{3 \times 2} = (-3)^6 = 729[/latex]
Principal Roots
Roots of Positive Numbers
- When the index of the root is even, any positive number will have two real number solutions, with one being the negative of the other. The positive solution is known as its principal root.
- For example, [latex]\sqrt{9}[/latex] has two roots: +3 and –3, because (3) × (3) = 9 and (−3) × (−3) = 9 This is usually written as ±3 and read as “plus or minus 3”, and the principal root is 3.
- [latex]\sqrt[4]{16}[/latex] has two roots: +2 and –2, because (2) × (2) × (2) × (2) = 16 and (–2) × (–2) × (–2) × (–2) = 16 i.e., the roots are ±2 and the principal root is 2.
- When the index of the root is odd, there is only one real number solution and it is positive. This positive solution is the principal root.
- For example, [latex]\sqrt[3]{27} = 3[/latex] because (3) × (3) × (3) = 27; i.e., the principal root is 3.
- Similary, [latex]\sqrt[5]{32} = 2[/latex] because (2) × (2) × (2) × (2) × (2) = 32; i.e., the principal root is 2.
Roots of Negative Numbers
- When the index of the root is even, there is no real number solution to any negative number.
- For example, [latex]\sqrt[4]{-81}[/latex] has no real roots.
- When the index of the root is odd, there is only one real number solution to any negative number and it is negative. This negative solution is the principal root.
- For example, [latex]\sqrt[5]{-32} = -2[/latex] because (−2) (−2) (−2) (−2) (−2) = −32; i.e., the principal root is –2.
Real Numbers
Real numbers include all positive numbers and negative numbers. A summary of the types of real numbers, which we have learned about in the last three chapters, is provided below:
Table 1.3-b: Types of Real Numbers
Note: Terminating decimals (decimals that end) and repeating decimals (decimals that do not end but show a repeating pattern) are also rational numbers because they can be expressed as a quotient of integers.
For example,
- [latex]0.375[/latex] can be expressed as [latex]\displaystyle{\frac{3}{8}}[/latex].
- [latex]0.185185...[/latex] is usually written as [latex]0.\overline{185}[/latex] and can be expressed as [latex]\displaystyle{\frac{5}{27}}[/latex].

1.3 Exercises
Answers to the odd-numbered problems are available at the end of the textbook.
For problems 1 to 6, place the correct sign ‘<’ or ‘>’ in the space between the following pairs of numbers indicated by the underscore.
- a. –5 _ 0 b. –2 _ +6
- a. 0 _ –3 b. –5 _ +3
- a. +8 _ –3 b. +1 _ –2
- a. –5 _+4 b. +3 _ –7
- a. –6 _ –8 b. –5 _ –2
- a. –7 _ –9 b. –8 _ –4
For problems, 7 to 10, arrange the numbers from least to greatest.
- a. 5, –6, 8, –8, –5, 2 b. –8, 4, –6, 3, –9, 7
- a. –2, –3, 5, 2, –1, 4 b. 15, –14, 17, 4, –5, –7
- a. 9, –5, –8, 3, 7, 10 b. 12, –13, 15, 2, –8, –3
- a. –3, 6, 1, –7, –1, 7 b. –12, 0, 12, –16, 15, –5]
Evaluate problems 11 to 30.
- a. [latex]–8 + (–5 – 7) [/latex]
b. [latex]2 – (–3) + 1[/latex] - a. [latex]–9 + (–3 – 8)[/latex]
b. [latex]5 – (–7) + 8[/latex] - a. [latex]–3 – (–7) + 8[/latex]
b. [latex](–4 + 9) – (–3 – 6)[/latex] - a. [latex]–7 – (–9) – 1 [/latex]
b. [latex](–5 + 3) + (–4 – 9)[/latex] - a. [latex]4 + (–3) – [5 + (–11)] [/latex]
b. [latex]–6 + (–4) – [–(15 – 8)][/latex] - a. [latex]5 + (–4) – [7 + (–9)] [/latex]
b. [latex]–8 + (–15) – [–(6 – 7)][/latex] - a. [latex]2(–3)(–5)[/latex]
b. [latex]–4(–3)(–2)[/latex] - a. [latex]6(–2)(–4)[/latex]
b. [latex]–5(–3)(–2)[/latex] - a. [latex]–64 ÷ (–8) [/latex]
b. [latex]45 ÷ (–5)[/latex] - a. [latex]–48 ÷ (–6)[/latex]
b. [latex]36 ÷ (–4)[/latex] - a. [latex]–5 + (–2)(–5) – (6 – 3)[/latex]
b. [latex]7(2 – 3) – 4(–7 + 1)[/latex] - a. [latex]–8(5 – 6) – 3(–6 + 2) [/latex]
b. [latex]–7 + (–3)(–4) – (–8 – 3)[/latex] - a. [latex](5 + 7)^2 - 5^2 - 7^2[/latex]
b. [latex]2^2 - 2^4 - 20 \times 3[/latex] - a. [latex](9 - 12)^2 - 9^2 - 12^2[/latex]
b. [latex]7 \times 8 - 3^2 - 2^3[/latex] - a. [latex](20 \times 4 - 8^2)^2 + 9[/latex]
b. [latex](3 \times 9 - 3^2) + 12[/latex] - a. [latex]-12 ÷ 4 - 3 \times 2^4[/latex]
b. [latex]-5 \times 3^3 \div 9 + 5^2[/latex] - [latex]-11^2 - 4 \times 54 \div (5 - 2)^3 - 3[/latex]
- [latex][(1 + 12)(1 - 5)]^2 \div (5 - 3 \times 2^2 - 4)[/latex]
- [latex]\displaystyle{-31 - [(15 \div 3) \times 32] \div \left(2^2 \times \frac{23}{46}\right)}[/latex]
- [latex]3(7^2 + 2 \times 15 \div 3) - (1 - 3 \times 4)^2[/latex]
Unless otherwise indicated, this chapter is an adaptation of the eTextbook Foundations of Mathematics (3rd ed.) by Thambyrajah Kugathasan, published by Vretta-Lyryx Inc., with permission. Adaptations include supplementing existing material and reordering chapters.