Answer Key – Chapter 8
Exercise 8.1
- a. Quadrant II
b. Quadrant IV
c. Quadrant I
- a. X-axis (left)
Quadrant III
Y-axis (up)
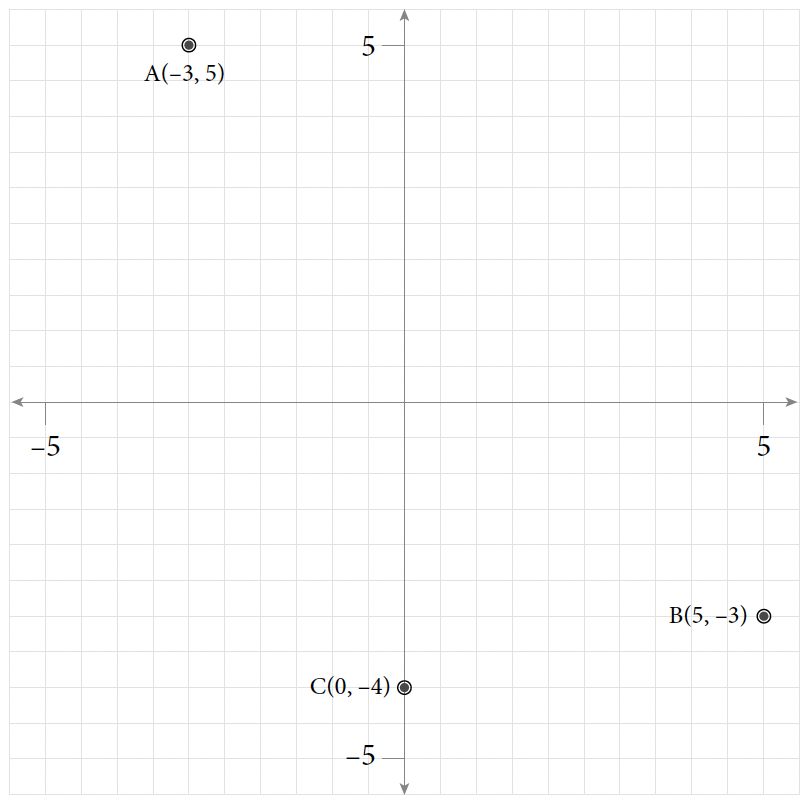
- D (–3, –1)
- S(–3, –1)
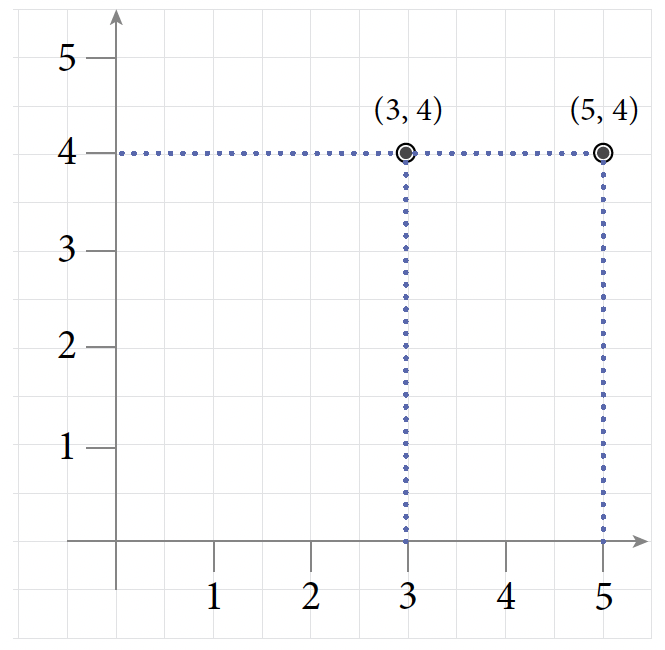
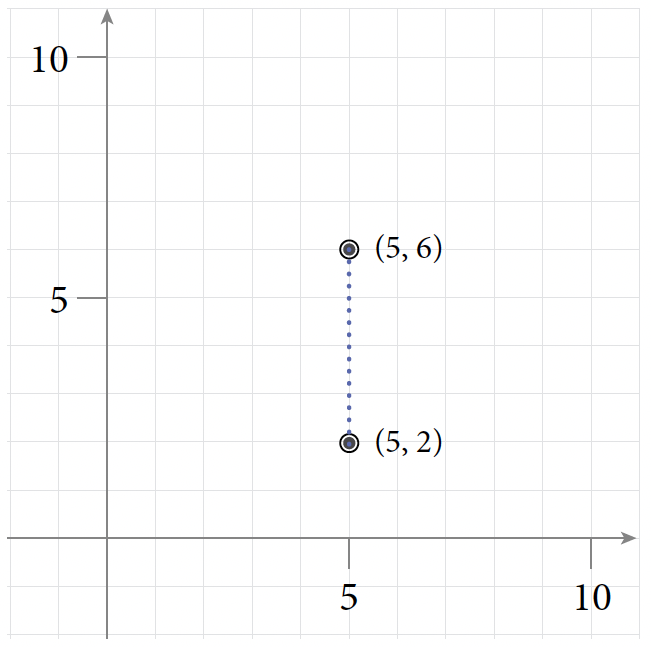
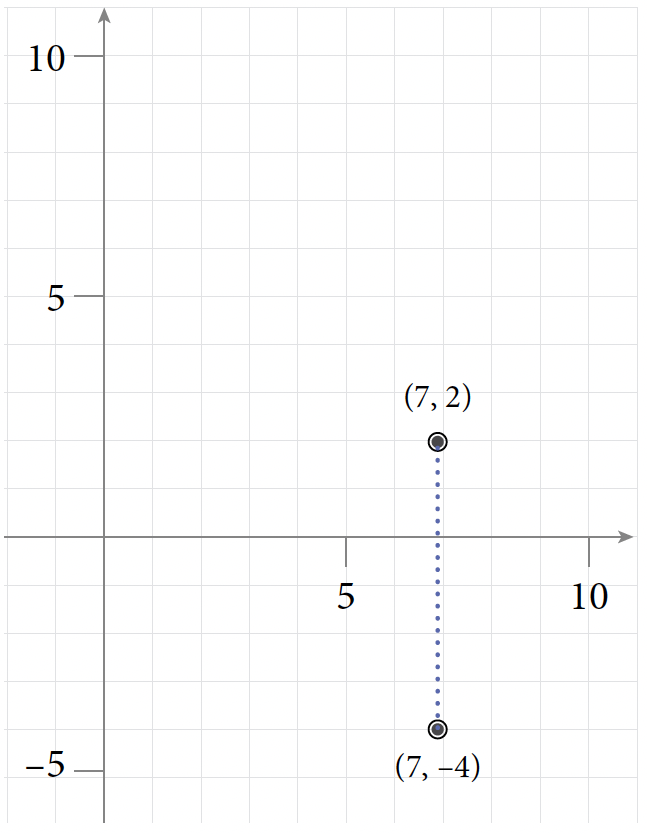
- (1, 12) and (1, –2)
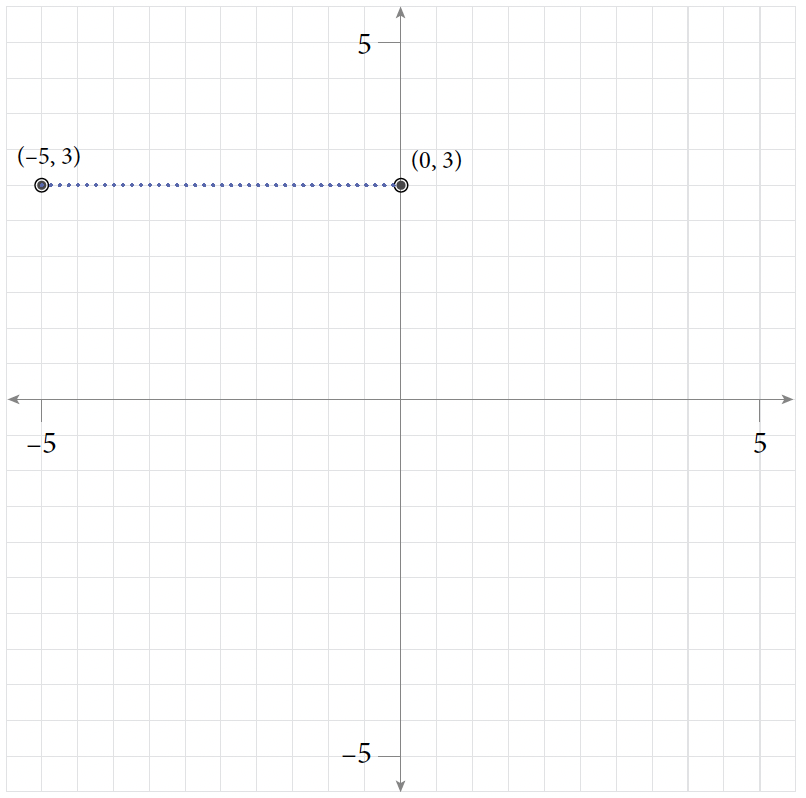
- (–7, 3) and (5, 3)
Exercise 8.2
- a. 4
b. 10
c. 6
d. 9
e. 15
f. 6
- a. –3
b. 3
c. 1
d. [latex]\displaystyle{\frac{3}{2}}[/latex]
e. 6
f. –6
- [latex]5x - 2y = -2[/latex]
- [latex]3x + 4y = -12[/latex]
- [latex]x - 2y = -3[/latex]
- [latex]\displaystyle{y = -\frac{3}{2}x - \frac{3}{4}}[/latex]
- [latex]\displaystyle{y = \frac{3}{2}x + 5}[/latex]
- [latex]\displaystyle{y = -\frac{3}{2}x + 3}[/latex]
-
Table of Values for Exercise 17 [latex]x[/latex] [latex]y[/latex] [latex](x, y)[/latex] [latex]0[/latex] [latex]3[/latex] [latex](0, 3)[/latex] [latex]1[/latex] [latex]4[/latex] [latex](1, 4)[/latex] [latex]2[/latex] [latex]5[/latex] [latex](2, 5)[/latex] [latex]3[/latex] [latex]6[/latex] [latex](3, 6)[/latex]
-
Table of Values for Exercise 19 [latex]x[/latex] [latex]y[/latex] [latex](x, y)[/latex] [latex]0[/latex] [latex]1[/latex] [latex](0, 1)[/latex] [latex]1[/latex] [latex]-4[/latex] [latex](1, -4)[/latex] [latex]2[/latex] [latex]-9[/latex] [latex](2, -9)[/latex] [latex]3[/latex] [latex]-14[/latex] [latex](3, -14)[/latex]
-
Table of Values for Exercise 21 [latex]x[/latex] [latex]y[/latex] [latex](x, y)[/latex] [latex]0[/latex] [latex]-1[/latex] [latex](0, -1)[/latex] [latex]1[/latex] [latex]-3[/latex] [latex](1, -3)[/latex] [latex]2[/latex] [latex]-5[/latex] [latex](2, -5)[/latex] [latex]3[/latex] [latex]-7[/latex] [latex](3, -7)[/latex]
-
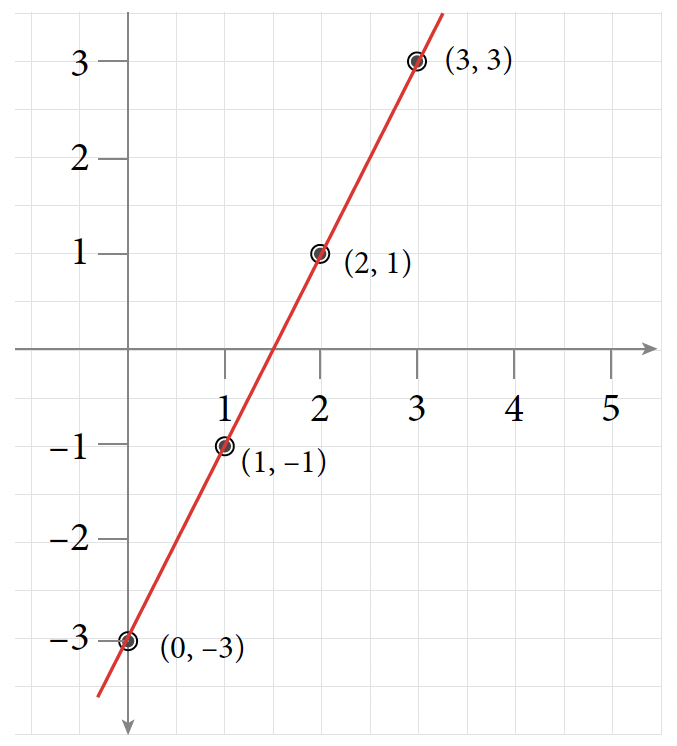
Table of Values for Exercise 23 [latex]x[/latex] [latex]y[/latex] [latex](x, y)[/latex] [latex]0[/latex] [latex]-3[/latex] [latex](0, -3)[/latex] [latex]1[/latex] [latex]-1[/latex] [latex](1, -1)[/latex] [latex]2[/latex] [latex]1[/latex] [latex](2, 1)[/latex] [latex]3[/latex] [latex]3[/latex] [latex](3, 3)[/latex]
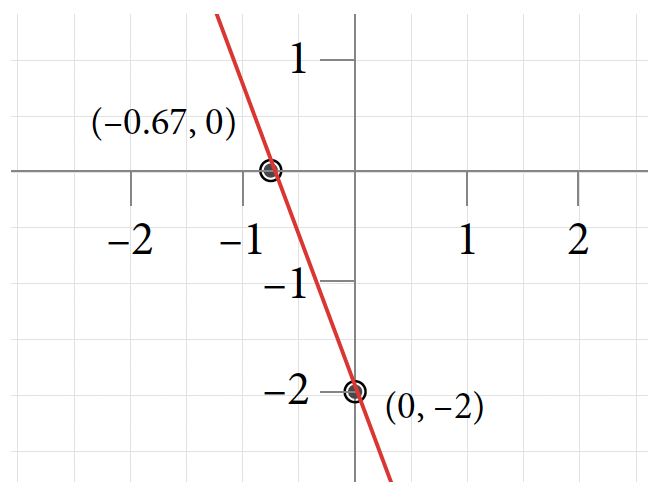
- x-intercept: [latex]\displaystyle{(-\frac{2}{3}, 0)}[/latex]; y-intercept: [latex]\displaystyle{(0, -2)}[/latex]
-
- Positive slope
- 0
- [latex]\displaystyle{-\frac{5}{8}}[/latex]
8.3 Exercise
-
- [latex]y = 2[/latex]
- [latex]y = x - 2[/latex]
- [latex]y = -2x + 10[/latex]
- [latex]\displaystyle{y = \frac{2}{3}x}[/latex]
- [latex]\displaystyle{y = -\frac{3}{2}x + 6}[/latex]
- 2
- 7
- [latex]5x + 3y = 15[/latex]
- [latex]2x + y = 1[/latex]
8.4 Exercise
-
- Perpendicular
- Parallel
- Perpendicular
- Neither
- [latex]\displaystyle{y = \frac{2}{3}x - \frac{13}{3}}[/latex]
- [latex]\displaystyle{y = \frac{1}{3}x - 20}[/latex]
- [latex]y = x + 7[/latex]
- [latex]\displaystyle{y = -\frac{1}{2}x + 1}[/latex]
Review Exercises 8
- a. Quadrant IV
b. Quadrant II
c. X-axis (right)
d. Quadrant IV
e. X-axis (right)
f. Y-axis (up)
-
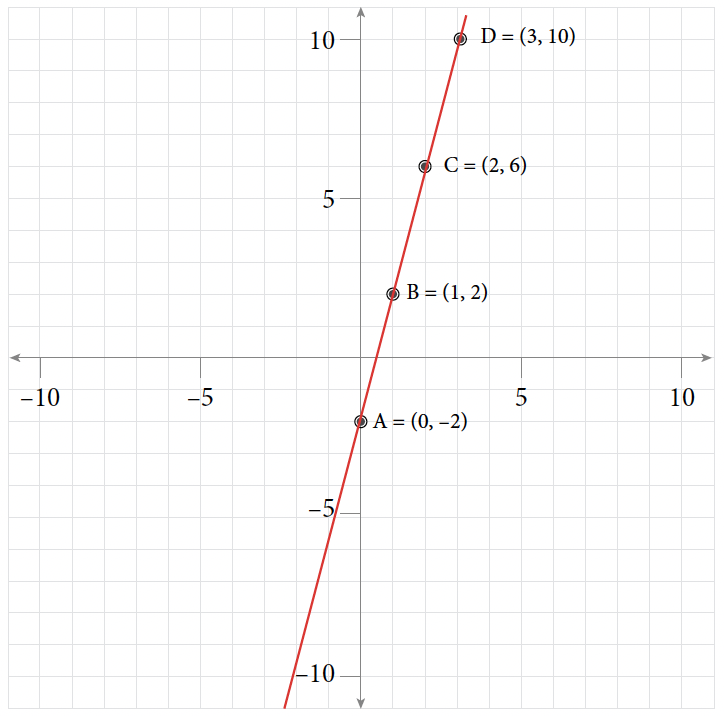
Table of Values for Exercise 5 [latex]x[/latex] [latex]y[/latex] [latex](x, y)[/latex] [latex]0[/latex] [latex]-2[/latex] [latex](0, -2)[/latex] [latex]1[/latex] [latex]2[/latex] [latex](1, 2)[/latex] [latex]2[/latex] [latex]6[/latex] [latex](2, 6)[/latex] [latex]3[/latex] [latex]10[/latex] [latex](3, 10)[/latex]
-
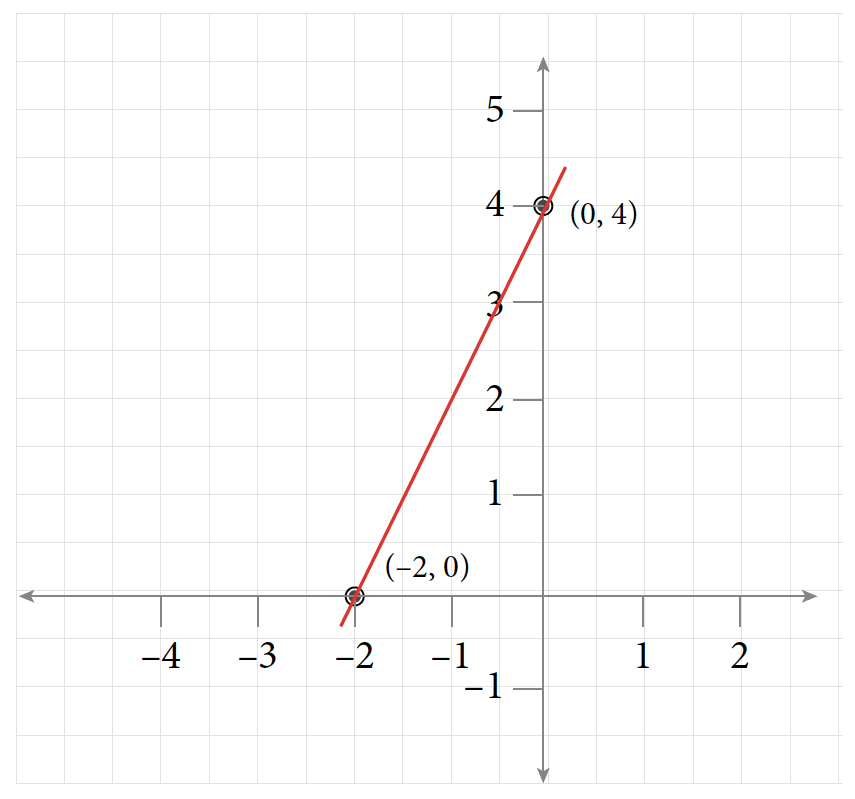
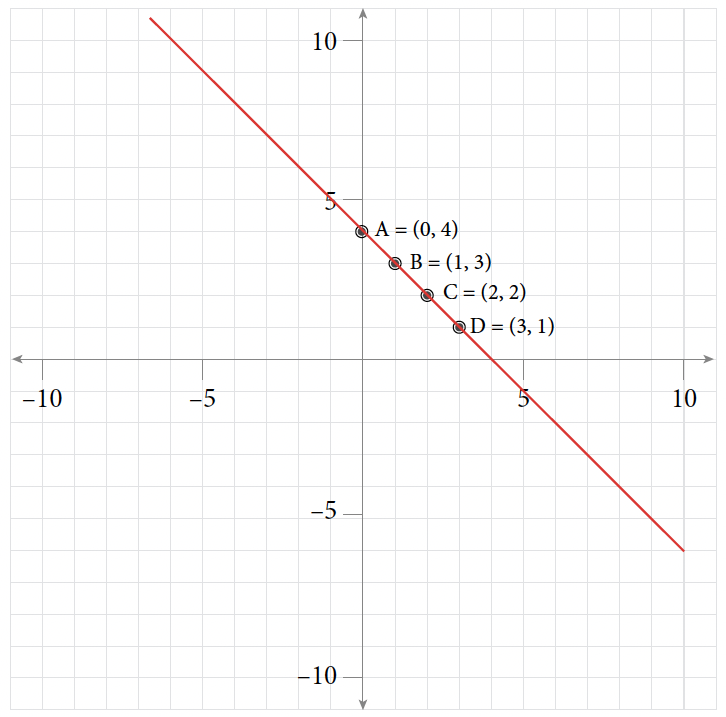
Table of Values for Exercise 7 [latex]x[/latex] [latex]y[/latex] [latex](x, y)[/latex] [latex]0[/latex] [latex]4[/latex] [latex](0, 4)[/latex] [latex]1[/latex] [latex]3[/latex] [latex](1, 3)[/latex] [latex]2[/latex] [latex]2[/latex] [latex](2, 2)[/latex] [latex]3[/latex] [latex]1[/latex] [latex](3, 1)[/latex]
-
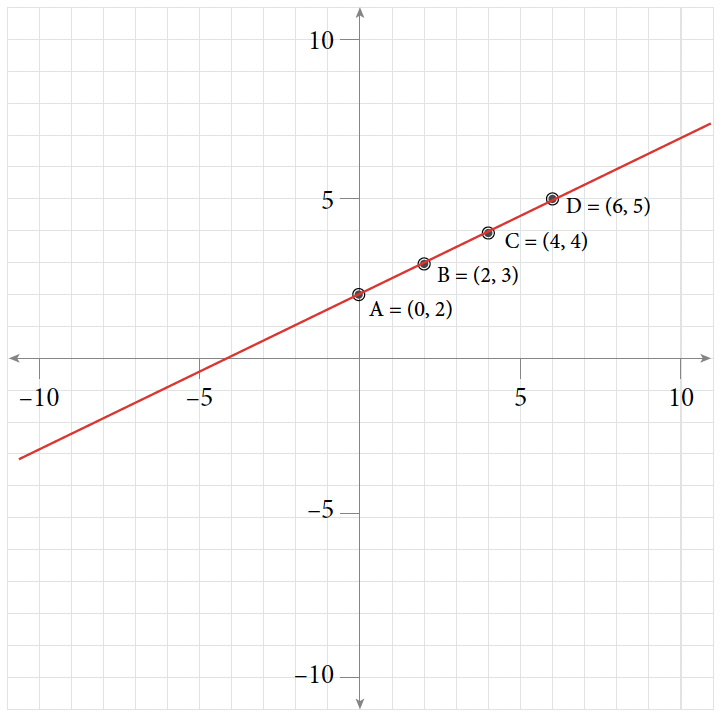
Table of Values for Exercise 9 [latex]x[/latex] [latex]y[/latex] [latex](x, y)[/latex] [latex]0[/latex] [latex]2[/latex] [latex](0, 2)[/latex] [latex]2[/latex] [latex]3[/latex] [latex](2, 3)[/latex] [latex]4[/latex] [latex]4[/latex] [latex](4, 4)[/latex] [latex]6[/latex] [latex]5[/latex] [latex](6, 5)[/latex]
-
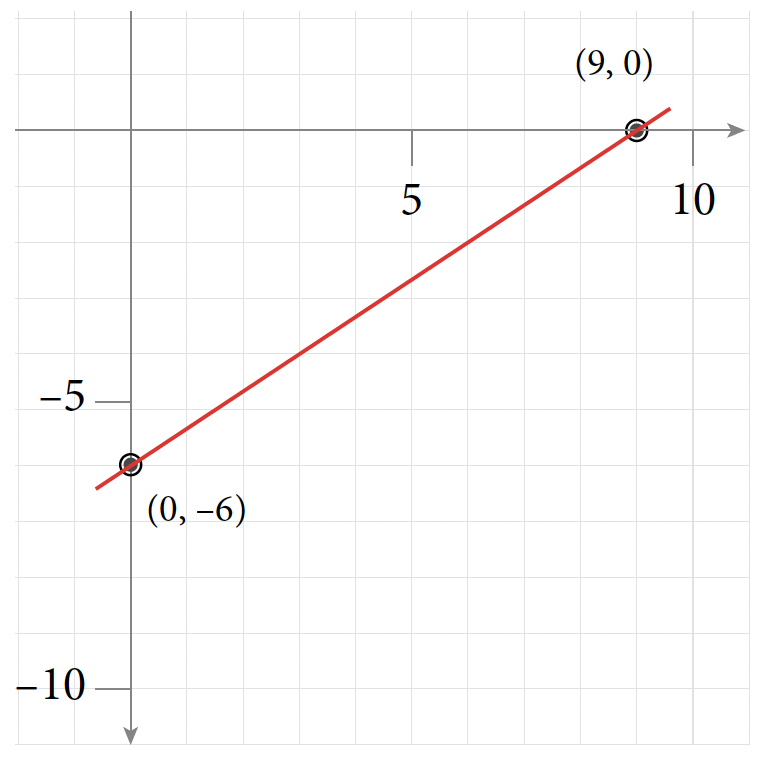
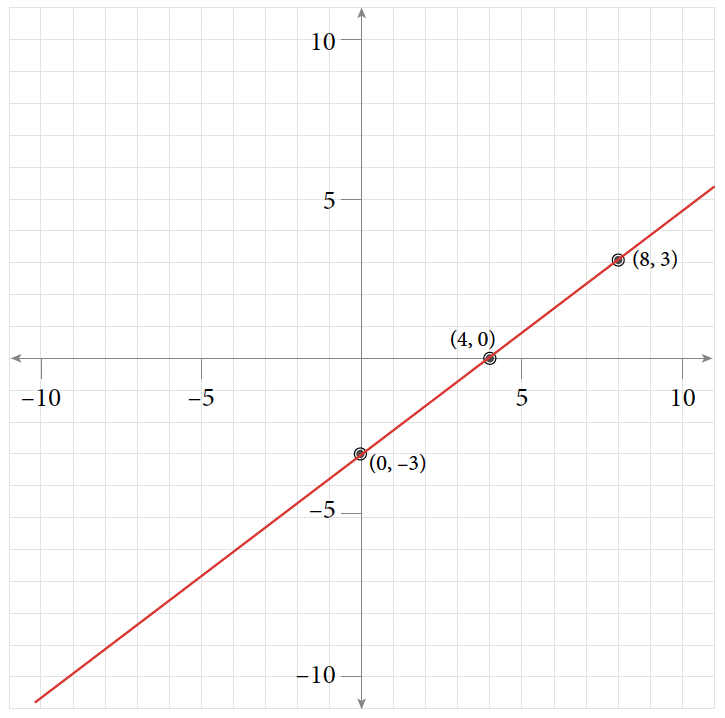
Table of Values for Exercise 11 [latex]x[/latex] [latex]y[/latex] [latex](x, y)[/latex] [latex]0[/latex] [latex]-3[/latex] [latex](0, -3)[/latex] [latex]4[/latex] [latex]0[/latex] [latex](4, 0)[/latex] [latex]8[/latex] [latex]3[/latex] [latex](8, 3)[/latex]
-
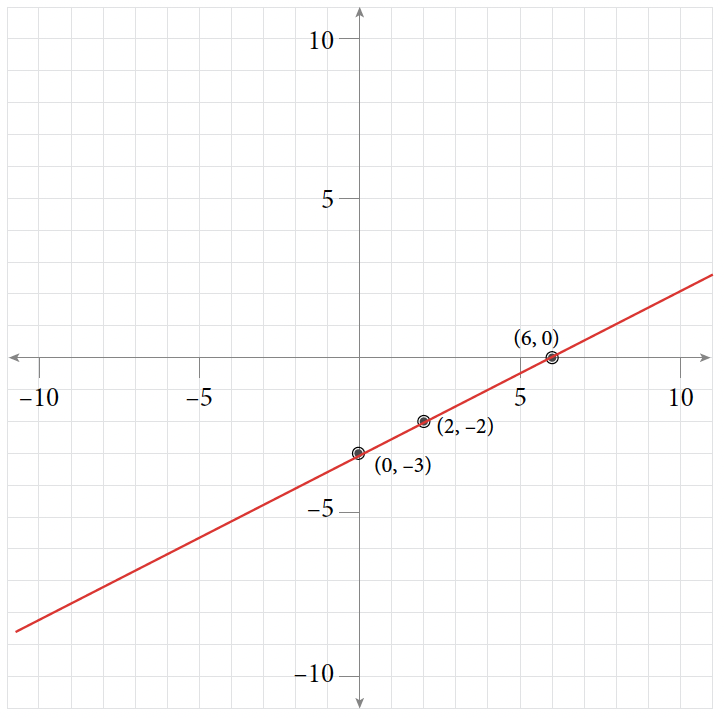
Table of Values for Exercise 13 [latex]x[/latex] [latex]y[/latex] [latex](x, y)[/latex] [latex]0[/latex] [latex]-3[/latex] [latex](0, -3)[/latex] [latex]6[/latex] [latex]0[/latex] [latex](6, 0)[/latex] [latex]2[/latex] [latex]-2[/latex] [latex](2, -2)[/latex]
-
Table of Values for Exercise 15 [latex]x[/latex] [latex]y[/latex] [latex](x, y)[/latex] [latex]0[/latex] [latex]0[/latex] [latex](0, 0)[/latex] [latex]1[/latex] [latex]4[/latex] [latex](1, 4)[/latex] 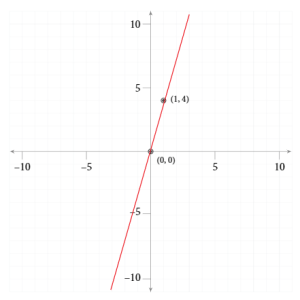
- [latex]\displaystyle{y = \frac{3}{4}x - \frac{1}{4}}[/latex]
- [latex]\displaystyle{y = -\frac{4}{3}x + \frac{8}{3}}[/latex]
- [latex]y = 3x - 5[/latex]
- [latex]\displaystyle{y = \frac{3}{4}x + \frac{9}{2}}[/latex]
- [latex]y = -2x + 1[/latex]
Self-Test Exercises 8
- [latex](-3, -1)[/latex]; Area = 40 square units
-
- [latex]2x - 3y = 6[/latex]
- [latex]\displaystyle{x = \frac{25}{8}}[/latex]
-
- [latex]\displaystyle{y = \frac{2}{3}x = 2}[/latex]
- [latex]\displaystyle{y = -\frac{3}{4}x + \frac{5}{4}}[/latex]
-
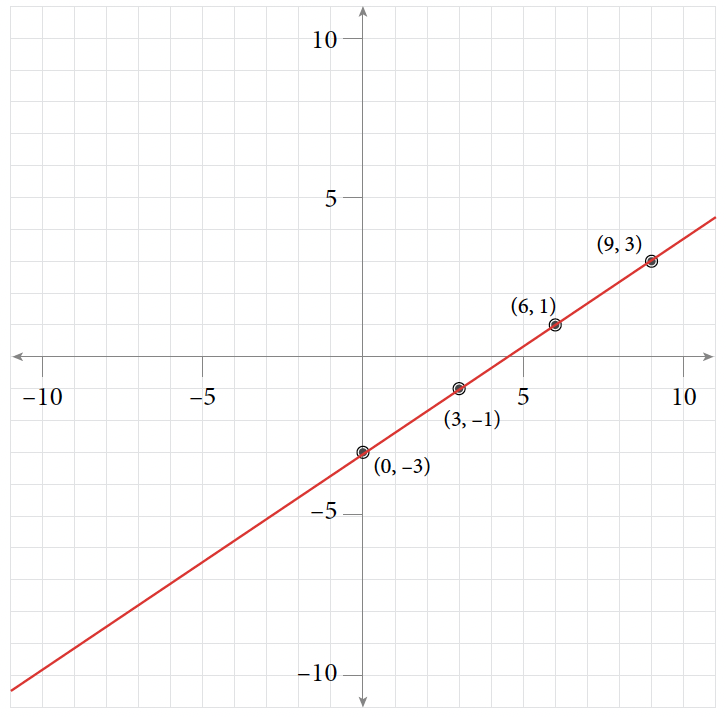
Table of Values for Self-Test Exercise 4 [latex]x[/latex] [latex]y[/latex] [latex](x, y)[/latex] [latex]0[/latex] [latex]-3[/latex] [latex](0, -3)[/latex] [latex]3[/latex] [latex]-1[/latex] [latex](3, -1)[/latex] [latex]6[/latex] [latex]1[/latex] [latex](6, 1)[/latex] [latex]9[/latex] [latex]3[/latex] [latex](9, 3)[/latex] -
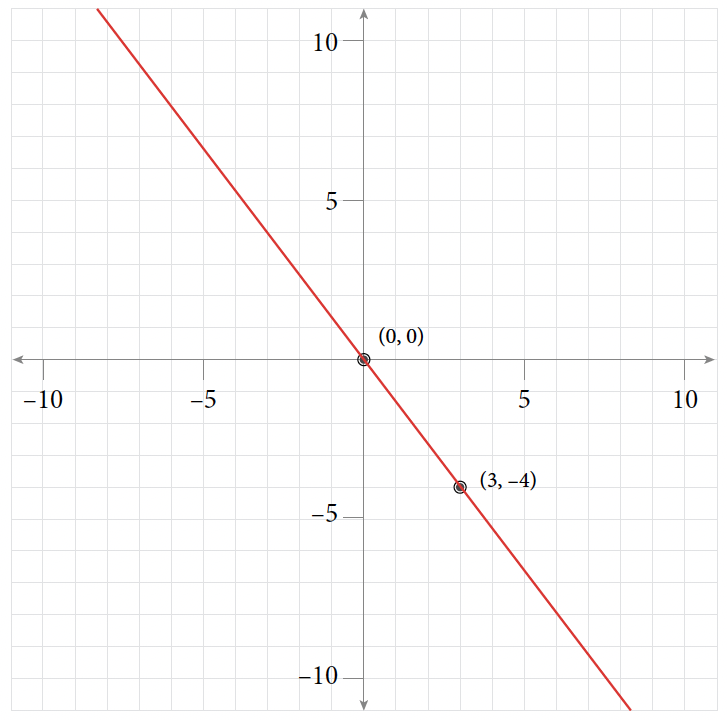
Table of Values for Self-Test Exercise 5 [latex]x[/latex] [latex]y[/latex] [latex](x, y)[/latex] [latex]0[/latex] [latex]0[/latex] [latex](0, 0)[/latex] [latex]3[/latex] [latex]-4[/latex] [latex](3, -4)[/latex] [latex]6[/latex] [latex]1[/latex] [latex](6, 1)[/latex]
- [latex]4x + 5y = 9[/latex]
- [latex]3x - 5y = 15[/latex]
- [latex]3x - 2y = -12[/latex]
- [latex]\frac{4}{3}x - y = 0[/latex]


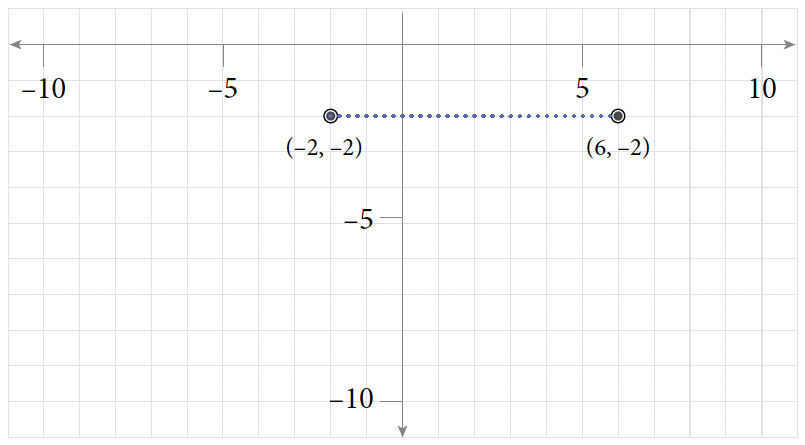






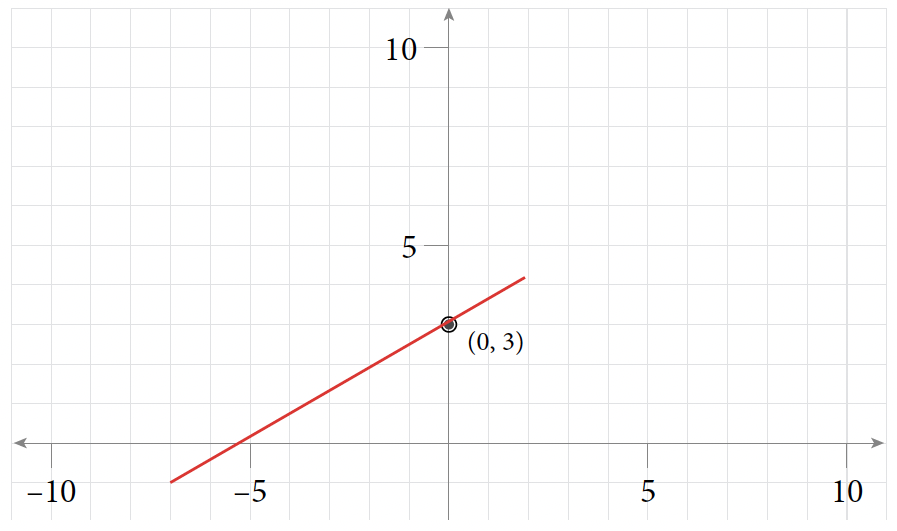

![Solution to Review Exercise 8-17. The y-intercept is (0,6). Using the slope, y-intercept method [latex]m = 4; b = 6[/latex], from the y-intercept move up 4 units and to the right 1 unit to get the next point.](https://ecampusontario.pressbooks.pub/app/uploads/sites/2884/2023/05/AK-RE-17.png)
![Solution to Review Exercise 8-19. The y-intercept is (0,6). Using the slope, y-intercept method [latex]\displaystyle{m = -\frac{3}{2}; b = 6}[/latex], from the y-intercept move up 3 units and to the right 2 units to get the next point.](https://ecampusontario.pressbooks.pub/app/uploads/sites/2884/2023/05/AK-RE-19.png)
![Solution to Review Exercise 8-21. The y-intercept is (0,-1). Using the slope, y-intercept method [latex]\displaystyle{m = -\frac{3}{4}; b = -1}[/latex], from the y-intercept move down 3 units and to the right 4 units to get the next point.](https://ecampusontario.pressbooks.pub/app/uploads/sites/2884/2023/05/AK-RE-21.png)