8. Case Study – Lightning Wholesale

Lightning Wholesale is a mid-to large-size company that works directly with manufacturers to bring sporting goods and equipment to mid to small-sized retailers.  The company is in Southern Ontario, Canada.  Lightning Wholesale acquires the goods, stores them in its warehouses, and distributes them to retailers, who then sell them to sporting enthusiasts across the province.  Suppliers are global, including those from the United States.

Lightning Wholesale is a dynamic office with global networking, communications, customer service, and complex workflows. Lighting Wholesale depends on its office professionals to support staff and management. Office Professional tasks include clerical support, bookkeeping, customer service, data analysis, and document processing.

Lightning Wholesale cares about its employees and retailers.  Where managers can assist their employees, they try to.  Where retailers need guidance, Lightning Wholesales tries to fill this gap as best they can. In working with its small retailers, many of which are owned and operated by sole proprietors, Lightning Wholesale assists the owners with their pricing to help develop promotional pricing plans and the amounts of the payments that can be advertised.  Lightning Wholesale freely offers help since it means more sales and increased profits for the company.

There are currently a few main tasks for Lightning Wholesale management:

• The payroll needs review for the past fiscal year.
• Costs and expenses need forecasting for the next fiscal year.
• Detailed analysis of office supply orders from quarter to quarter with recommendations for the next fiscal year.
• Forklifts need replacing in the warehouse.
• The next round of co-op students needs a computer.
• The employee appreciation event needs planning for next year.
• Travel expenses for the mobile team need to be summarized for the last fiscal year.

The equation [latex]y = \displaystyle{\frac{1}{4}}x +1.25[/latex] represents the relationship between the number of employees and office supply expenses.

• y represents the office supply expenses
• x represents the number of employees
• m is the slope of the line, representing the rate of change in expenses per employee
• b is the y-intercept, representing the fixed expenses with zero employees

Questions

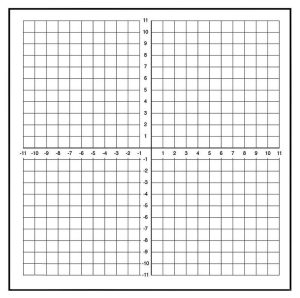
1. Graph the linear equation [latex]y = \displaystyle{\frac{1}{4}}x +1.25[/latex]. Copy the following graph on your paper, and label the x and y axis and the line representing the relationship between the number of employees and office supply expenses.

2. Is the slope positive or negative? What does the slope tell us about the relationship between the number of employees and the office supply expense?

3. What happens with the office supply expense if Lightning Wholesale hires more employees?

4. Lightning Wholesale would like to lower the office supply expense for next year. If it is decided that the amount of office expense per employee will be lowered, will the linear equation change – will the slope change?

5. After reviewing past and current expenses, the management team has decided to decrease the office supply expense per employee. The new linear equation represents the relationship between the number of employees and office supply expenses: [latex]y = \displaystyle{\frac{1}{2}}x +1.25[/latex]. Draw the new linear equation on your graph and compare the 2 lines.

• What happens to y when x increases?
• Why are the slopes different? What does this indicate?