5.2 Proportions
The Proportion Equation
When two ratios are equivalent, we say that they are proportional to each other. In the proportion equation, the ratio on the left side of the equation is equivalent to the ratio on the right side of the equation.
Consider an example where A : B is 50 : 100 and C : D is 30 : 60.
Reducing the ratios to lowest terms, we obtain the ratio of A : B as 1 : 2 and the ratio of C : D as 1 : 2.
Since these ratios are equivalent, they are proportional to each other, and their proportion equation is:
[latex]\boldsymbol{A : B = C : D}[/latex]
The proportion equation can also be formed by representing the ratios as fractions.
Equating the fraction obtained by dividing the first term by the second term on the left side, to the one obtained by dividing the first term by the second term on the right side, we obtain:
[latex]\boldsymbol{\displaystyle{\frac{A}{B} = \frac{C}{D}}}[/latex]
This proportion equation can be simplified by multiplying both sides of the equation by the product of both denominators, which is B × D.
[latex]\displaystyle{\frac{A}{B} = \frac{C}{D}}[/latex] Multiplying both sides by (B × D),
[latex]\displaystyle{\frac{A}{B}(B \times D) = \frac{C}{D}(B \times D)}[/latex] Simplifying,
[latex]AD = BC[/latex]
The same result can be obtained by equating the product of the numerator of the first ratio and the denominator of the second ratio with the product of the denominator of the first ratio and the numerator of the second ratio. This is referred to as cross-multiplication and is shown below:
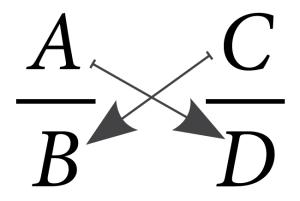
Cross-multiplying,
[latex]AD = BC[/latex]
Notice that the cross-multiplication of [latex]\displaystyle{\frac{A}{C} = \frac{B}{D}}[/latex] also gives the same result of [latex]AD = BC[/latex]. Therefore, [latex]A : B = C : D[/latex] is equivalent to both [latex]\displaystyle{\frac{A}{B} = \frac{C}{D}}[/latex] and [latex]\displaystyle{\frac{A}{C} = \frac{B}{D}}[/latex]. If any three terms of the proportion equation are known, the fourth term can be calculated.
Proportion Equation With Sets of Ratios Having More Than Two Terms
Consider the proportion equation [latex]A : B : C = D : E : F[/latex].
This proportion equation can also be expressed using fractions: [latex]\displaystyle{\frac{A}{B} = \frac{D}{E}}[/latex], [latex]\displaystyle{\frac{B}{C} = \frac{E}{F}}[/latex], and [latex]\displaystyle{\frac{A}{C} = \frac{D}{F}}[/latex]
Cross-multiplying leads to: [latex]AE = BD[/latex], [latex]BF = CE[/latex], and [latex]AF = CD[/latex]
The proportion [latex]A : B : C = D : E : F[/latex] can be illustrated by the table below,
| 1st Term | 2nd Term | 3rd Term |
|---|---|---|
| A | B | C |
| D | E | F |
and expressed as, [latex]A : D = B : E = C : F[/latex].
Expressing using fractions, [latex]\displaystyle{\frac{A}{D} = \frac{B}{E} = \frac{C}{F}}[/latex]
Cross-multiplying leads to the same result as shown above: [latex]AE = BD, BF = CE, and AF = CD[/latex].
Therefore, [latex]A : B : C = D : E : F[/latex] is equivalent to both
- [latex]\displaystyle{\frac{A}{B} = \frac{D}{E}, \frac{B}{C} = \frac{E}{F}, \frac{A}{C} = \frac{D}{F}}[/latex], and
- [latex]\displaystyle{\frac{A}{D} = \frac{B}{E} = \frac{C}{F}}[/latex]
Example 5.2-a: Solving for the Unknown Quantity in Proportions
Determine the missing term in the following proportions:
- [latex]4 : 5 = 8 : x[/latex]
- [latex]6 : x = 10 : 25[/latex]
- [latex]x : 1.9 = 2.6 : 9.88[/latex]
- [latex]\displaystyle{3 : 3\frac{3}{4} = x : 5\frac{1}{4}}[/latex]
Solution
- [latex]4 : 5 = 8 : x[/latex]
Using fractional notation, [latex]\displaystyle{\frac{4}{5} = \frac{8}{x}}[/latex] or [latex]\displaystyle{\frac{4}{8} = \frac{5}{x}}[/latex].
Cross-multiplying, [latex]4x = 40[/latex].
Simplifying, [latex]\displaystyle{x = \frac{40}{4}}[/latex].
Therefore, [latex]x = 10[/latex].Solution Breakdown for Example 5.2-a A 1st Term 2nd Term 4 5 8 x - [latex]6 : x = 10 : 25[/latex]
Using fractional notation, [latex]\displaystyle{\frac{6}{x} = \frac{10}{25}}[/latex] or [latex]\displaystyle{\frac{6}{10} = \frac{x}{25}}[/latex].
Cross-multiplying, [latex]150 = 10x[/latex].
Simplifying, [latex]\displaystyle{x = \frac{150}{10}}[/latex].
Therefore, [latex]x = 15[/latex].Solution Breakdown for Example 5.2-a B 1st Term 2nd Term 6 x 10 25 - [latex]x : 1.9 = 2.6 : 9.88[/latex]
Using fractional notation, [latex]\displaystyle{\frac{x}{1.9} = \frac{2.6}{9.88}}[/latex] or [latex]\displaystyle{\frac{x}{2.6} = \frac{1.9}{9.88}}[/latex].
Cross-multiplying, [latex]9.88x = 4.94[/latex].
Simplifying, [latex]\displaystyle{x = \frac{4.94}{9.88}}[/latex].
Therefore, [latex]x = 0.5[/latex].Solution Breakdown for Example 5.2-a C 1st Term 2nd Term x 1.9 2.6 9.88 - [latex]\displaystyle{3 : 3\frac{3}{4} = x : 5\frac{1}{4}}[/latex]
Rewriting as an improper fraction, [latex]\displaystyle{3 : \frac{15}{4} = x : \frac{21}{4}}[/latex].
Multiplying both sides by 4, [latex]12 : 15 = 4x : 21[/latex].
Using fractional notation, [latex]\displaystyle{\frac{12}{15} = \frac{4x}{21}}[/latex] or [latex]\displaystyle{\frac{12}{4x} = \frac{15}{21}}[/latex].
Cross-multiplying, [latex]252 = 60x[/latex].
Simplifying, [latex]\displaystyle{x = \frac{252}{60}}[/latex].
Therefore, [latex]\displaystyle{x = \frac{21}{5} = 4\frac{1}{5}}[/latex].Solution Breakdown for Example 5.2-a D 1st Term 2nd Term 12 15 4x 21
Example 5.2-b: Solving Word Problems Using Proportions
Express each of the following ratios in its simplest form:
- The distance (in km) that Ben can walk in [latex]\displaystyle{3\frac{1}{2}}[/latex] hours.
- How long (in hours and minutes) will it take him to walk 15 km?
Solution
- Calculating the distance (in km) he can walk in [latex]\displaystyle{3\frac{1}{2}}[/latex] hours. km : h = km : h[latex]\displaystyle{9 : 2 = x : 3\frac{1}{2}}[/latex].
Rewriting as an improper fraction, [latex]\displaystyle{9 : 2 = x : \frac{7}{2}}[/latex].
Multiplying both sides by 2, [latex]18 : 4 = 2x : 7[/latex].
Using fractional notation, [latex]\displaystyle{\frac{18}{4} = \frac{2x}{7}}[/latex] or [latex]\displaystyle{\frac{18}{2x} = \frac{4}{7}}[/latex].
Cross-multiplying, [latex]126 = 8x[/latex].
Simplifying, [latex]\displaystyle{x = \frac{126}{8}}[/latex][latex]x = 15.75 km[/latex].
Therefore, Ben can walk a distance of 15.75 km in [latex]\displaystyle{3\frac{1}{2}}[/latex] hours.Solution Breakdown for Example 5.2-b A 1st Term 2nd Term 18 4 2x 7 - Calculating the time (in hours and minutes) that it will take him to walk 15 km: km : h = km : h [latex]9 : 2 = 15 : x[/latex]
Using fractional notation, [latex]\displaystyle{\frac{9}{2} = \frac{15}{x}}[/latex] or [latex]\displaystyle{\frac{9}{15} = \frac{2}{x}}[/latex].
Cross-multiplying, [latex]9x = 30[/latex].
Simplifying, [latex]\displaystyle{x = \frac{30}{9} = 3\frac{1}{3}}[/latex][latex]\displaystyle{x = 3 h + \left(\frac{1}{3} \times 60\right) min}[/latex][latex]x = 3 h 20 min[/latex].
Therefore, Ben can walk 15 km in 3 hours and 20 minutes.Solution Breakdown for Example 5.2-b B 1st Term 2nd Term 9 2 15 x
Example 5.2-c: Sharing Using Proportions
Andrew (A), Brandon (B), and Chris (C) decide to form a partnership to start a snow removal business together. A invests $31,500, B invests $42,000, and C invests $73,500. They agree to share the profits in the same ratio as their investments.
- What is the ratio of their investments, expressed in lowest terms?
- In the first year of running the business, A's profit was $27,000. What were B's and C's profits?
Solution
- Ratio of their investments :A : B : C 31,500 : 42,000 : 73,500.
Dividing each term by the common factor of 100,315 : 420 : 735.
Dividing each term by the common factor of 5,63 : 84 : 147.
Dividing each term by the common factor of 7,9 : 12 : 21.
Dividing each term by the common factor of 3,3 : 4 : 7.
Therefore, the ratio of their investments is 3 : 4 : 7. - A's profit was $27,000. B's and C's profits are calculated using one of the two methods, as follows:
Method 1: Ratio of Investment = Ratio of Profit A : B : C = A : B : C
Substituting terms, [latex]3 : 4 : 7 = 27,000 : x : y[/latex].
Using fractional notation, [latex]\displaystyle{\frac{3}{4} = \frac{27,000}{x}}[/latex] and [latex]\displaystyle{\frac{3}{7} = \frac{27,000}{y}}[/latex].
Cross-multiplying, [latex]3x = 108,000[/latex] [latex]3y = 189,000[/latex].
Simplifying, [latex]x = \$36,000.00[/latex] [latex]y = \$63,000.00[/latex].
Method 2: Ratio of Investment = Ratio of Profit A : B : C = A : B : CSubstituting terms, [latex]3 : 4 : 7 = 27,000 : x : y[/latex].Using fractional notation, [latex]\displaystyle{\frac{3}{27,000} = \frac{4}{x} = \frac{7}{y}}[/latex].Hence, [latex]\displaystyle{\frac{3}{27,000} = \frac{4}{x}}[/latex] and [latex]\displaystyle{\frac{3}{27,000} = \frac{7}{y}}[/latex].Cross-multiplying, [latex]3x = 108,000[/latex] [latex]3y = 189,000[/latex].Simplifying, [latex]x = \$36,000.00[/latex] [latex]y = \$63,000.00[/latex].Therefore, B's profit is $36,000, and C's profit is $63,000.
| 1st Term | 2nd Term | 3rd Term |
|---|---|---|
| 3 | 4 | 7 |
| 27,000 | x | y |
5.2 Exercises
Answers to the odd-numbered questions are available at the end of the book.
For problems 1 and 2, determine whether the ratio pairs are in proportion.
- a. 6 : 9 and 14 : 21
b. 5 : 15 and 2 : 8
c. 18 : 24 and 12 : 16
d. 12 : 60 and 6 : 24
- a. 9 : 12 and 4 : 3
b. 10 : 30 and 8 : 24
c. 14 : 20 and 28 : 42
d. 15 : 12 and 24 : 30
For problems 3 to 6, solve the proportion equations for the unknown value.
- a. [latex]x : 4 = 27 : 36[/latex]
b. [latex]24 : x = 6 : 9[/latex]
c. [latex]5 : 9 = x : 3[/latex]
d. [latex]1 : 2 = 5 : x[/latex]
- [latex]x : 8 = 6 : 24[/latex]
- [latex]3 : x = 18 : 42[/latex]
- [latex]15 : 5 = x : 15[/latex]
- [latex]28 : 35 = 4 : x[/latex]
- a. [latex]\displaystyle{x : 18\frac{1}{4} = 8 : 11\frac{3}{4}}[/latex]
b. [latex]\displaystyle{7\frac{1}{5} : x = 5\frac{3}{4} : 3\frac{2}{5}}[/latex]
c. [latex]\displaystyle{1 : 4\frac{1}{2} = x : 2\frac{3}{4}}[/latex]
d. latex] \displaystyle{1\frac{1}{2} : 2\frac{1}{4} = 1\frac{3}{4} : x} [/latex]
- a. [latex]x : 3.65 = 5.5 : 18.25[/latex]
b. [latex]2.2 : x = 13.2 : 2.5[/latex]
c. [latex]4.25 : 1.87 = x : 2.2[/latex]
e. [latex]2.4 : 1.5 = 7.2 : x[/latex]
- A truck requires 96 litres of gas to cover 800 km. How many litres of gas will it require to cover 1,500 km? br
- Based on Alvin's past experience, it would take his team five months to complete two projects. How long would his team take to complete eight similar projects?
- Eric paid a property tax of $3,600 for his land that measures 330 square metres. Using the same tax rate, what would his neighbour's property tax be if the size of the house is 210 square metres and is taxed at the same rate?
- The city of Brampton charges $1,750 in taxes per year for a 2,000 square metre farm. How much would Maple Farms have to pay in taxes if they had a 12,275 square metre farm in the same area?
- On a map, 4 cm represents 5.0 km. If the distance between Town A and Town B on the map is 9.3 cm, how many kilometres apart are these towns?
- On a house plan, 1.25 cm represents 3 metres. If the actual length of a room is 5.4 metres, how will this length be represented in the plan in cm?
- Steve invested his savings in a GIC, mutual funds, and a fixed deposit in the ratio of 5 : 4 : 3, respectively. If he invested $10,900 in mutual funds, calculate his investments in the GIC and the fixed deposit.
- The ratio of the distance from An's house to Mark, Jeff, and Justin's houses is 3 : 5.25 : 2, respectively. If the distance from Ann's house to Mark's is 9.50 km, calculate the distance from Ann's house to Justin's and Ann's house to Jeff's.
- A, B, and C, started a business with investments in the ratio of 5 : 4 : 3, respectively. A invested $25,000, and all three of them agreed to share profits in the ratio of their investments.
- Calculate B and C's investments.
- If A's profit was $30,000 in the first year, calculate B and C's profits.
- A, B, and C formed a partnership and invested in the ratio of 7 : 9 : 5, respectively. They agreed to share the profit in the ratio of their investments. A invested $350,000.
- Calculate B and C's investments in the partnership.
- In the first year, if A made $38,500 in profit from the partnership, how much did B and C make?
Unless otherwise indicated, this chapter is an adaptation of the eTextbook Foundations of Mathematics (3rd ed.) by Thambyrajah Kugathasan, published by Vretta-Lyryx Inc., with permission. Adaptations include supplementing existing material and reordering chapters.

