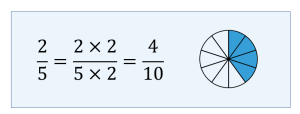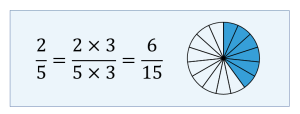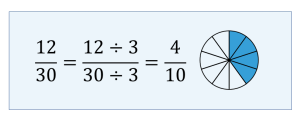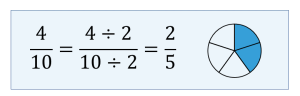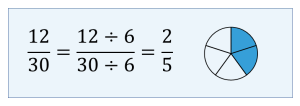2.3 Fractions
If we divide one whole unit into several equal portions, then one or more of these equal portions can be represented by a fraction.
A fraction is composed of the following three parts:
- Numerator: the number of equal parts of a whole unit.
- Fraction bar: the division sign, meaning ‘divided by’.
- Denominator: the total number of equal parts into which the whole unit is divided.
For example, [latex]\displaystyle{\frac{3}{8}}[/latex] is a fraction.
The numerator ‘3’ indicates that the fraction represents 3 equal parts of a whole unit, and the denominator ‘8’ indicates that the whole unit is divided into 8 equal parts, as shown above. The fraction bar indicates that the numerator ‘3’ is divided by the denominator ‘8’.
[latex]\displaystyle{\frac{3}{8}}[/latex] is read as “three divided by eight”, “three-eighths”, or “three over eight”. All of these indicate that 3 is the numerator, 8 is the denominator, and the fraction represents 3 of 8 pieces of the whole. The numerator and denominator are referred to as the terms of the fraction.
Note: The denominator of a fraction cannot be zero since a number cannot be divided into zero equal parts.
Any number that can be represented as a fraction is known as a rational number.
For example,
- [latex]\displaystyle{\frac{2}{3}}[/latex], [latex]\displaystyle{\frac{5}{2}}[/latex], and [latex]\displaystyle{\frac{7}{1}}[/latex] are rational numbers.
- The whole number 7 can be written as the fraction [latex]\displaystyle{\frac{7}{1}}[/latex]; therefore, 7 is also a rational number.
Fractions can be represented on a number line. They are plotted in-between whole numbers.
For example, [latex]\displaystyle{\frac{1}{2}}[/latex] is represented on a number line as:
When one unit is divided into two equal portions, each portion represents one-half of that unit. One of such equal portions is written as [latex]\displaystyle{\frac{1}{2}}[/latex].
Example 2.3-a: Representing Fractions on a Number Line
Represent the following fractions on a number line:
- [latex]\displaystyle{\frac{2}{3}}[/latex]
- [latex]\displaystyle{\frac{3}{5}}[/latex]
Solution
-
When one unit is divided into five equal portions, each portion represents one-fifth of that unit. Three of such equal portions is three-fifths and is written as [latex]\displaystyle{\frac{3}{5}}[/latex].

Types of Fractions
Proper Fractions
A proper fraction is a fraction in which the numerator is less than the denominator.
For example,
Improper Fractions
An improper fraction is a fraction in which the numerator is greater than or equal to the denominator; i.e., the value of the entire fraction is more than 1.
For example,
-
[latex]\displaystyle{\frac{7}{4}}[/latex] is an improper fraction because the numerator 7 is greater than the denominator 4
(i.e., 7 > 4, or [latex]\displaystyle{\frac{7}{4}}[/latex] > 1).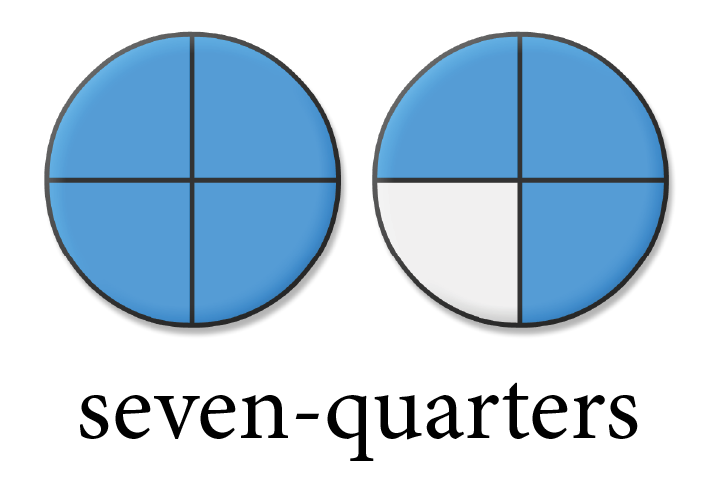
Mixed Numbers (or Mixed Fractions)
A mixed number consists of both a whole number and a proper fraction, written side-by-side, which implies that the whole number and the proper fraction are added.
For example,
Relationship Between Mixed Numbers and Improper Fractions
Converting a Mixed Number to an Improper Fraction
Follow these steps to convert a mixed number to an improper fraction:
Step 1: Multiply the whole number by the fraction's denominator and add this value to the fraction's numerator.
Step 2: The resulting answer will be the numerator of the improper fraction.
Step 3: The denominator of the improper fraction is the same as the denominator of the original fraction in the mixed number.
Example: Convert [latex]3{\frac{5}{8}}[/latex] to an improper fraction.
Step 1: 3(8) = 24
Step 2: 24 + 5 = 29. The numerator will be 29.
Step 3: The denominator will be 8.
Therefore, [latex]3{\frac{5}{8}}[/latex] = [latex]\displaystyle{\frac{29}{8}}[/latex]
Note: You can perform the above steps in a single line of arithmetic as follows:
[latex]3{\frac{5}{8}}[/latex] = [latex]\displaystyle{\frac{3(8) + 5}{8}}[/latex] = [latex]\displaystyle{\frac{24 + 5}{8}}[/latex] = [latex]\displaystyle{\frac{29}{8}}[/latex]
Four circles are divided into 8 equal pieces. Three of the four circles are completely shaded, and five pieces of the last circle are shaded for 29 pieces.
Converting an Improper Fraction to a Mixed Number
Follow these steps to convert an improper fraction to a mixed number:
Step 1: Divide the numerator by the denominator.
Step 2: The quotient becomes the whole number, and the remainder becomes the numerator of the fraction portion of the mixed number.
Step 3: The denominator of the fraction portion of the mixed number is the same as the denominator of the original improper fraction.
Example: Convert [latex]\displaystyle{\frac{29}{8}}[/latex] to an improper fraction.
Step 1: Divide 29 by 8.
Step 2: The quotient (3) becomes the whole number, and the remainder (5) becomes the numerator of the fraction portion of the mixed number.
Step 3: The denominator of the fraction portion of the mixed number (8) is the same as the denominator of the original improper fraction (8).
[latex]\begin{array}{r} 3 &&\hbox{Quotient}\\ 8\enclose{longdiv}{29}\\ -24 \\ \hline 5 &&\hbox{Remainder}\\ \end{array}[/latex]
Therefore, [latex]\displaystyle{\frac{29}{8}}[/latex] = [latex]3{\frac{5}{8}}[/latex]
Equivalent Fractions
When a fraction's numerator and denominator are either multiplied by the same number or divided by the same number, the result is a new fraction known as an equivalent fraction. Equivalent fractions have the same value.
That is, the same part (or portion) of a whole unit can be represented by different fractions.
For example,

[latex]\displaystyle{\frac{1}{2}}[/latex], [latex]\displaystyle{\frac{2}{4}}[/latex], [latex]\displaystyle{\frac{3}{6}}[/latex], [latex]\displaystyle{\frac{4}{8}}[/latex], [latex]\displaystyle{\frac{5}{10}}[/latex], ... are equivalent fractions.
Example 2.3-b: Finding Equivalent Fractions by Raising to Higher Terms
Find two equivalent fractions of [latex]\displaystyle{\frac{2}{5}}[/latex] by raising to higher terms.
Solution
To find an equivalent fraction of [latex]\displaystyle{\frac{2}{5}}[/latex], multiply both the numerator and denominator by 2. The resulting equivalent fraction is [latex]\displaystyle{\frac{4}{10}}[/latex].
To find an equivalent fraction of [latex]\displaystyle{\frac{2}{5}}[/latex], multiply both the numerator and denominator by 3. The resulting equivalent fraction is [latex]\displaystyle{\frac{6}{15}}[/latex].
Example 2.3-c: Finding Equivalent Fractions by Reducing to Lower Terms
Find two equivalent fractions of [latex]\displaystyle{\frac{12}{30}}[/latex] by reducing to lower terms.
Solution
To find an equivalent fraction of [latex]\displaystyle{\frac{12}{30}}[/latex], divide both the numerator and denominator by 3. The resulting equivalent fraction is [latex]\displaystyle{\frac{4}{10}}[/latex].
Therefore, [latex]\displaystyle{\frac{4}{10}}[/latex] and [latex]\displaystyle{\frac{2}{5}}[/latex] are equivalent fractions of [latex]\displaystyle{\frac{12}{30}}[/latex].
Note: The fraction [latex]\displaystyle{\frac{2}{5}}[/latex] cannot be further reduced, as 2 and 5 do not have any common factors.
Therefore, [latex]\displaystyle{\frac{2}{5}}[/latex] is a fraction in its lowest (or simplest) terms. We will learn more about this further in the section.
Identifying Equivalent Fractions Using Cross Products
If the cross products of two fractions are equal, then the two fractions are equivalent fractions, and vice versa (i.e., if the fractions are equivalent, then their cross products are equal).
That is, if [latex]\displaystyle{\frac{a}{b}}[/latex] = [latex]\displaystyle{\frac{c}{d}}[/latex], then a × d = b × c
a × d and b × c are known as cross products
For example, [latex]\displaystyle{\frac{3}{5}}[/latex] and [latex]\displaystyle{\frac{12}{20}}[/latex] are equivalent fractions because their cross products, 3 × 20 and 5 × 12, are equal:
3 × 20 = 60
5 × 12 = 60
Example 2.3-d: Classifying Fractions as Equivalent or Not Equivalent
Classify the pair of fractions as ‘equivalent’ or ‘not equivalent’ by using their cross products.
- [latex]\displaystyle{\frac{2}{5}}[/latex] and [latex]\displaystyle{\frac{12}{20}}[/latex]
- [latex]\displaystyle{\frac{5}{4}}[/latex] and [latex]\displaystyle{\frac{20}{12}}[/latex]
- [latex]\displaystyle{\frac{3}{8}}[/latex] and [latex]\displaystyle{\frac{9}{24}}[/latex]
Solution
-
[latex]\displaystyle{\frac{2}{5}}[/latex] and [latex]\displaystyle{\frac{12}{20}}[/latex]
The cross products are 2 × 30 and 5 × 12.
2 × 30 = 60
5 × 12 = 60
Therefore, the two fractions are equivalent.
The cross-products are equal.
-
[latex]\displaystyle{\frac{5}{4}}[/latex] and [latex]\displaystyle{\frac{20}{12}}[/latex]
The cross products are 5 × 12 and 4 × 20.
5 × 12 = 60
4 × 20 = 80
Therefore, the two fractions are not equivalent.
The cross products are not equal.
-
[latex]\displaystyle{\frac{3}{8}}[/latex] and [latex]\displaystyle{\frac{9}{24}}[/latex]
The cross products are 3 × 24 and 8 × 9.
3 × 24 = 72
8 × 9 = 72
Therefore, the two fractions are equivalent.
The cross-products are equal.
Fractions in Lowest (or Simplest) Terms
Dividing a fraction's numerator and denominator by the same number, which results in an equivalent fraction, is known as reducing or simplifying the fraction.
For example, we saw in Example 2.1-c that [latex]\displaystyle{\frac{4}{10}}[/latex] and [latex]\displaystyle{\frac{2}{5}}[/latex] are reduced fractions of [latex]\displaystyle{\frac{12}{30}}[/latex].
A fraction in which the numerator and denominator have no factors in common (other than 1) is said to be a fraction in its lowest (or simplest) terms.
Any fraction can be fully reduced to its lowest terms by one of the following two methods:
Method 1: Dividing the numerator and denominator by the greatest common factor (GCF).
Method 2: Writing the numerator and denominator as products of prime factors and reducing by the common prime factors.
Example 2.3-e: Reducing Fractions to their Lowest Terms
Reduce the following fractions to their lowest terms.
- [latex]\displaystyle{\frac{40}{45}}[/latex]
- [latex]\displaystyle{\frac{54}{24}}[/latex]
Solution
a. [latex]\displaystyle{\frac{40}{45}}[/latex]
Method 1: Factors of 40 are: 1, 2, 4, 5, 8, 10, 20, and 40. Factors of 45 are: 1, 3, 5, 9, 15, and 45. The GCF is 5. Dividing the numerator and denominator by the GCF, 5,
[latex]\displaystyle{\frac{40}{45} = \frac{40 ÷ 5}{45 ÷ 5} = \frac{8}{9}}[/latex]
Method 2: Prime factors of 40 are: 2 × 2 × 2 × 5. Prime factors of 45 are: 3 × 3 × 5. The common prime factor is one 5. Therefore, [latex]\displaystyle{\frac{40}{45}}[/latex] is equal to [latex]\displaystyle{\frac{8}{9}}[/latex] reduced to its lowest terms.
b. [latex]\displaystyle{\frac{54}{24}}[/latex]
Method 1: Factors of 54 are: 1, 2, 3, 6, 9, 18, 27, and 54. Factors of 24 are: 1, 2, 3, 4, 6, 8, 12, and 24. The GCF is 6. Dividing the numerator and denominator by the GCF, 6,
[latex]\displaystyle{\frac{54}{24} = \frac{54 ÷ 6}{24 ÷ 6} = \frac{9}{4}}[/latex]
Method 2: Prime factors of 54 are: 2 × 3 × 3 × 3. Prime factors of 24 are: 2 × 2 × 2 × 3. The common prime factors are one 2 and one 3.Therefore, [latex]\displaystyle{\frac{54}{24}}[/latex] is equal to [latex]\displaystyle{\frac{9}{4}}[/latex] reduced to its lowest terms.
Reciprocals of Fractions
Two numbers whose product equals 1 are known as reciprocals of each other. Every non-zero real number has a reciprocal.
For example,
- [latex]\displaystyle{\frac{2}{3}}[/latex] and [latex]\displaystyle{\frac{3}{2}}[/latex] are reciprocals of each other because [latex]\displaystyle{\frac{2}{3} × \frac{3}{2} = 1}[/latex]
When the numerator and denominator of a fraction are interchanged, the resulting fraction is the reciprocal of the original fraction.
For example,
- 5 and [latex]\displaystyle{\frac{1}{5}}[/latex] are reciprocals (5 can also be written as [latex]\displaystyle{\frac{5}{1}}[/latex]).
- Similarly, the reciprocal of[latex]\displaystyle{\frac{-2}{5}}[/latex] is [latex]\displaystyle{\frac{5}{-2} = -\frac{5}{2}}[/latex]
The reciprocal of a positive number is always positive and the reciprocal of a negative number is always negative.
Note:
- The reciprocal of a number is not the negative of that number. (The reciprocal of [latex]3 ≠ -3[/latex]. The reciprocal of [latex]\displaystyle{3 = \frac{1}{3}}[/latex].)
- The reciprocal of a fraction is not an equivalent fraction of that fraction.(The reciprocal of [latex]\displaystyle{\frac{2}{5} ≠ \frac{4}{10}}[/latex]. The reciprocal of [latex]\displaystyle{\frac{2}{5} = \frac{5}{2}}[/latex].)
Table 2.3-a: Examples of Numbers with their Negatives and Reciprocals
| Number | 5 | −3 | [latex]\displaystyle{\frac{2}{3}}[/latex] | [latex]\displaystyle{-\frac{3}{8}}[/latex] |
|---|---|---|---|---|
| Negative of the Number |
−5 | 3 | [latex]\displaystyle{-\frac{2}{3}}[/latex] | [latex]\displaystyle{\frac{3}{8}}[/latex] |
| Reciprocal of the Number |
[latex]\displaystyle{\frac{1}{5}}[/latex] | [latex]\displaystyle{-\frac{1}{3}}[/latex] | [latex]\displaystyle{\frac{3}{2}}[/latex] | [latex]\displaystyle{-\frac{8}{3}}[/latex] |
2.3 Exercises
Answers to the odd-numbered problems are available at the end of the textbook.
- a. [latex]\displaystyle{\frac{16}{35}}[/latex]
b. [latex]3\frac{2}{9}[/latex] - a. [latex]15\frac{12}{13}[/latex]
b. [latex]\displaystyle{\frac{29}{30}}[/latex] - a. [latex]\displaystyle{\frac{19}{16}}[/latex]
b. [latex]9\frac{7}{8}[/latex] - a. [latex]\displaystyle{\frac{21}{22}}[/latex]
b. [latex]\displaystyle{\frac{52}{25}}[/latex] - a. [latex]4\frac{2}{5}[/latex]
b. [latex]\displaystyle{\frac{7}{3}}[/latex] - a. [latex]6\frac{1}{2}[/latex]
b. [latex]\displaystyle{\frac{20}{75}}[/latex]
- a. [latex]2\frac{2}{7}[/latex]
b. [latex]3\frac{1}{8}[/latex] - a. [latex]3\frac{2}{5}[/latex]
b. [latex]7\frac{5}{8}[/latex] - a. [latex]5\frac{4}{5}[/latex]
b. [latex]6\frac{3}{4}[/latex] - a. [latex]4\frac{3}{7}[/latex]
b.[latex]9\frac{5}{6}[/latex]
- a. [latex]\displaystyle{\frac{19}{7}}[/latex]
b. [latex]\displaystyle{\frac{45}{8}}[/latex] - a. [latex]\displaystyle{\frac{23}{7}}[/latex]
b. [latex]\displaystyle{\frac{34}{3}}[/latex] - a. [latex]\displaystyle{\frac{23}{3}}[/latex]
b. [latex]\displaystyle{\frac{31}{6}}[/latex] - a. [latex]\displaystyle{\frac{26}{4}}[/latex]
b. [latex]\displaystyle{\frac{29}{5}}[/latex]
- [latex]\displaystyle{\frac{44}{5}}[/latex] and [latex]4\frac{4}{5}[/latex]
- [latex]\displaystyle{\frac{47}{8}}[/latex] and [latex]5\frac{7}{8}[/latex]
- [latex]11\frac{5}{7}[/latex] and [latex]7\frac{5}{7}[/latex]
- [latex]\displaystyle{\frac{41}{4}}[/latex] and [latex]10\frac{3}{4}[/latex]
- [latex]\displaystyle{\frac{54}{7}}[/latex] and [latex]7\frac{5}{7}[/latex]
- [latex]\displaystyle{\frac{17}{8}}[/latex] and [latex]2\frac{3}{8}[/latex]
- [latex]\displaystyle{\frac{37}{9}}[/latex] and [latex]4\frac{1}{9}[/latex]
- [latex]\displaystyle{\frac{45}{11}}[/latex] and [latex]4\frac{3}{11}[/latex]
- [latex]\displaystyle{\frac{15}{4}}[/latex] and [latex]3\frac{1}{4}[/latex]
- [latex]\displaystyle{\frac{43}{6}}[/latex] and [latex]7\frac{5}{6}[/latex]
- [latex]\displaystyle{\frac{18}{5}}[/latex] and [latex]3\frac{3}{5}[/latex]
- [latex]\displaystyle{\frac{45}{7}}[/latex] and [latex]6\frac{3}{7}[/latex]
- [latex]3\frac{8}{9}[/latex] and [latex]\displaystyle{\frac{35}{9}}[/latex]
- [latex]\displaystyle{\frac{34}{8}}[/latex] and [latex]4\frac{1}{8}[/latex]
- [latex]\displaystyle{\frac{41}{12}}[/latex] and [latex]3\frac{5}{12}[/latex]
- [latex]7\frac{3}{9}[/latex] and [latex]\displaystyle{\frac{67}{9}}[/latex]
- a. [latex]\displaystyle{\frac{30}{20}}[/latex]
b. [latex]\displaystyle{\frac{48}{84}}[/latex] - a. [latex]\displaystyle{\frac{44}{12}}[/latex]
b. [latex]\displaystyle{\frac{42}{70}}[/latex] - a. [latex]\displaystyle{\frac{56}{48}}[/latex]
b. [latex]\displaystyle{\frac{84}{21}}[/latex] - a. [latex]\displaystyle{\frac{75}{105}}[/latex]
b. [latex]\displaystyle{\frac{144}{48}}[/latex] - a. [latex]\displaystyle{\frac{36}{63}}[/latex]
b. [latex]\displaystyle{\frac{60}{96}}[/latex] - a. [latex]\displaystyle{\frac{131}{84}}[/latex]
b. [latex]\displaystyle{\frac{54}{126}}[/latex]
- [latex]\displaystyle{\frac{6}{12}}[/latex] and [latex]\displaystyle{\frac{15}{30}}[/latex]
- [latex]\displaystyle{\frac{6}{10}}[/latex] and [latex]\displaystyle{\frac{9}{15}}[/latex]
- [latex]\displaystyle{\frac{8}{10}}[/latex] and [latex]\displaystyle{\frac{15}{12}}[/latex]
- [latex]\displaystyle{\frac{12}{18}}[/latex] and [latex]\displaystyle{\frac{18}{27}}[/latex]
- [latex]\displaystyle{\frac{15}{12}}[/latex] and [latex]\displaystyle{\frac{36}{45}}[/latex]
- [latex]\displaystyle{\frac{35}{15}}[/latex] and [latex]\displaystyle{\frac{28}{12}}[/latex]
- [latex]\displaystyle{\frac{20}{25}}[/latex] and [latex]\displaystyle{\frac{24}{30}}[/latex]
- [latex]\displaystyle{\frac{16}{24}}[/latex] and [latex]\displaystyle{\frac{25}{30}}[/latex]
- a.[latex]\displaystyle{\frac{4}{9} = \frac{?}{27}}[/latex]
b. [latex]\displaystyle{\frac{4}{9} = \frac{20}{?}}[/latex] - a.[latex]\displaystyle{\frac{42}{36} = \frac{14}{?}}[/latex]
b. [latex]\displaystyle{\frac{42}{36} = \frac{?}{30}}[/latex] - a.[latex]\displaystyle{\frac{9}{12} = \frac{18}{?}}[/latex]
b. [latex]\displaystyle{\frac{9}{12} = \frac{?}{4}}[/latex] - a.[latex]\displaystyle{\frac{45}{75} = \frac{?}{25}}[/latex]
b. [latex]\displaystyle{\frac{45}{75} = \frac{18}{?}}[/latex] - a.[latex]\displaystyle{\frac{3}{2} = \frac{12}{?}}[/latex]
b. [latex]\displaystyle{\frac{3}{2} = \frac{?}{12}}[/latex] - a.[latex]\displaystyle{\frac{25}{15} = \frac{?}{3}}[/latex]
b. [latex]\displaystyle{\frac{25}{15} = \frac{35}{?}}[/latex]
- What fraction of 1 year is 4 months?
- What fraction of 1 hour is 25 minutes?
- Karen cut a pizza into 16 equal slices and served 12 slices to her friends. What fraction of the pizza was served?
- Out of 35 students in a math class, 15 received an ‘A’ in their final exam. What fraction of the students in the class received an ‘A’ grade?
- In a survey of 272 people, 68 people responded ‘yes’ and the remaining responded ‘no’. What fraction of the people responded ‘no’?
- In a finance math course with 490 students, 70 students failed the final exam. What fraction of the students passed the final exam in this course?
- Out of the 480 units in a condominium tower, 182 are rented. What fraction of the units are not rented?
- In a community of 6,000 people, 1,800 were 60 years or older. What fraction of the people were below the age of 60 years?
Unless otherwise indicated, this chapter is an adaptation of the eTextbook Foundations of Mathematics (3rd ed.) by Thambyrajah Kugathasan, published by Vretta-Lyryx Inc., with permission. Adaptations include supplementing existing material and reordering chapters.