2.3 Present Value of Annuities
Learning Objectives
- Calculate the present value of an ordinary annuity
- Calculate the present value of an annuity due
Formula & Symbol Hub
Symbols Used
- [latex]FV[/latex] = Future value or maturity value
- [latex]PV[/latex] = Present value of principal
- [latex]PMT[/latex] = Annuity payment amount
- [latex]I/Y[/latex] = Nominal interest rate
- [latex]P/Y[/latex] = Number of payments per year or payment frequency
- [latex]C/Y[/latex] = Number of compounds per year or compounding frequency
- [latex]n[/latex] or [latex]N[/latex] = Total number of annuity payments
Formulas Used
-
Formula 2.1 - Total Number of Payments (Annuity)
[latex]n=P/Y \times t[/latex]
-
Formula 2.2 - Future Value of Ordinary Annuity
[latex]FV=PMT \times \left[\frac{(1+i_2)^n-1}{i_2}\right][/latex]
-
Formula 2.3 - Future Value of Annuity Due
[latex]FV=PMT \times (1+i_2) \times \left[\frac{(1+i_2)^n-1}{i_2}\right][/latex]
-
Formula 2.4 - Present Value of Ordinary Annuity
[latex]PV=PMT \times \left[\frac{1-(1+i_2)^{-n}}{i_2}\right][/latex]
-
Formula 2.5 - Present Value of Annuity Due
[latex]PV=PMT \times (1+i_2) \times \left[\frac{1-(1+i_2)^{-n}}{i_2}\right][/latex]
Introduction
The present value of any annuity is equal to the sum of the present values of all the annuity payments when they are moved to the beginning of the first payment interval. For example, assume you will receive [latex]\$1,000[/latex] annual payments at the end of every payment interval for the next three years from an investment earning [latex]10\%[/latex] compounded annually. How much money needs to be in the annuity at the start to make this happen? To find out how much money you need in the investment to sustain these payments, you would apply the fundamental concept of the time value of money to move each payment amount to the start of the first payment interval (the focal date) and sum the values to arrive at the present value.
Although you could use this technique to solve all present value of an annuity situations, the computations become increasingly cumbersome as the number of payments increases. In the above example, what if the person instead received quarterly payments of [latex]\$250[/latex] for three years? That is [latex]12[/latex] payments over three years, resulting in [latex]12[/latex] separate present value calculations. Or if they received monthly payments, the [latex]36[/latex] payments over three years would result in [latex]36[/latex] separate present value calculations! Clearly, solving this would be tedious and time consuming—not to mention prone to error.
[latex]\boxed{2.4}[/latex] Present Value of Ordinary Annuities
[latex]{\color{red}{PV}}\;\text{is the Present Value of the Annuity:}[/latex] The present value is the sum of the present value of all of the annuity payments at the start of the first payment interval.
[latex]{\color{blue}{PMT}}\;\text{is the Annuity Payment:}[/latex] The amount of money that is invested or paid after each payment interval.
[latex]{\color{green}{i_2}}\;\text{is the Periodic Interest Rate:}[/latex] for the interest rate whose compounding frequency matches the payment frequency}. If the annuity is a simple annuity, the compounding frequency and the payment frequency are equal and the given interest rate can be used to calculate the periodic interest rate. If the annuity is a general annuity, the compounding frequency and the payment frequency are different and an interest conversion must be done first to find the equivalent interest rate with the compounding frequency equal to the payment frequency.
[latex]{\color{purple}{n}}\;\text{is the Total Number of Payments made during the Annuity:}[/latex] [latex]n=P/Y \times t[/latex] where [latex]P/Y[/latex] is the payment frequency and [latex]t[/latex] is the time in years.
The amount of interest ([latex]I[/latex]) earned by the annuity is
[latex]\displaystyle{I=n \times PMT-PV}[/latex]
Key Takeaways
In a simple annuity, the payment frequency and the compounding frequency are equal ([latex]P/Y=C/Y[/latex]). In this situation the periodic interest rate [latex]i_2=\frac{j}{m}[/latex] where [latex]j[/latex] is the nominal interest rate given in the question and [latex]m[/latex] is the compounding frequency (and the payment frequency).
In a general annuity, the payment frequency and the compounding frequency are not equal ([latex]P/Y \neq C/Y[/latex]). In this situation, the given interest rate must first be converted to the equivalent interest rate where the new compounding frequency equals the payment frequency. Using the equivalent interest rate, calculate the periodic interest rate [latex]i_2[/latex].
Example 2.3.1
Rodriguez is planning on having an annual gross income of [latex]\$50,000[/latex] at the end of every year when he retires at age [latex]65[/latex]. He is planning for the account to be emptied by age [latex]78[/latex], which is the average life expectancy for a Canadian man. If the account earns [latex]5.1\%[/latex] compounded annually, how much money needs to be in the account when he retires? How much interest will he receive from the fund?
Solution
The timeline for Rodriguez's account appears below.

Step 1:The given information is
The payments are at the end of the payment intervals, and both the compounding frequency and the payment frequency are the same (both annually). This is an ordinary simple annuity. Because this is a simple annuity, an interest rate conversion is not required.
[latex]\begin{eqnarray*} PMT & = & \$50,000 \\ P/Y & = & 1 \\ I/Y & = & 5.1\% \\ C/Y & = & 1 \\ t & = & 13 \mbox{ years} \end{eqnarray*}[/latex]
Step 2: Calculate the periodic interest rate.
[latex]\begin{eqnarray*} i_2 & = & \frac{I/Y}{C/Y} \\ & = & \frac{5.1\%}{1}\\ & = & 5.1\%\end{eqnarray*}[/latex]
Step 3: Calculate the number of payments.
[latex]\begin{eqnarray*} n & = & P/Y \times t \\ & = & 1 \times 13 \\ & = & 13 \end{eqnarray*}[/latex]
Step 4: Calculate the present value.
[latex]\begin{eqnarray*} PV & = & PMT \times \left[1-\frac{(1+i_2)^{-n}}{i_2}\right] \\ & = & 50,000 \times \left[ \frac{1-(1+0.051)^{-13}}{0.051}\right] \\ & = & \$466,863.69 \end{eqnarray*}[/latex]
Step 5: Calculate the interest earned.
[latex]\begin{eqnarray*} I & = & n \times PMT-PV \\ & = & 13 \times 50,000-466,863.69 \\ & = & \$183,136.31 \end{eqnarray*}[/latex]
Step 6: Write as a statement.
Rodriguez will need to have [latex]\$466,863.69[/latex] in his account when he turns [latex]65[/latex] if he wants to receive [latex]13[/latex] years of [latex]\$50,000[/latex] payments. He will receive [latex]\$183,136.31[/latex] in interest from the fund.
[latex]\boxed{2.5}[/latex] Present Value of Annuities Due
[latex]{\color{red}{PV}}\;\text{is the Present Value of the Annuity:}[/latex] The present value is the sum of the present value of all of the annuity payments at the start of the first payment interval.
[latex]{\color{blue}{PMT}}\;\text{is the Annuity Payment:}[/latex] The amount of money that is invested or paid after each payment interval.
[latex]{\color{green}{i_2}}\;\text{is the Periodic Interest Rate:}[/latex] for the interest rate whose compounding frequency matches the payment frequency. If the annuity is a simple annuity, the compounding frequency and the payment frequency are equal and the given interest rate can be used to calculate the periodic interest rate. If the annuity is a general annuity, the compounding frequency and the payment frequency are different and an interest conversion must be done first to find the equivalent interest rate with the compounding frequency equal to the payment frequency.
[latex]{\color{purple}{n}}\;\text{is the Total Number of Payments made during the Annuity:}[/latex] [latex]n=P/Y \times t[/latex] where [latex]P/Y[/latex] is the payment frequency and [latex]t[/latex] is the time in years.
The amount of interest ([latex]I[/latex]) earned by the annuity is
[latex]\displaystyle{I=n \times PMT-PV}[/latex]
Key Takeaways
The steps required to solve the present value of an annuity due are identical to those you use for an ordinary annuity except you use the formula for the present value of an annuity due. If the payment setting is NOT specified in the question, it is assumed that the payments come at the end of the interval.
Example 2.3.2
Tom has a savings account that earns [latex]6\%[/latex] compounded monthly. How much money does Tom need in his account today in order to receive beginning-of-month payments of [latex]\$250[/latex] for the next two years? How much interest does Tom receive?
Solution
Step 1: The given information is
The payments are at the beginning of the payment intervals, and both the compounding frequency and the payment frequency are the same (both monthly). This is a simple annuity due. Because this is a simple annuity, an interest rate conversion is not required.
[latex]\begin{eqnarray*} PMT & = & \$250 \\ P/Y & = & 1 2\\ I/Y & = & 6\% \\ C/Y & = & 12 \\ t & = & 2 \mbox{ years} \end{eqnarray*}[/latex]
Step 2: Calculate the periodic interest rate.
[latex]\begin{eqnarray*} i_2 & = & \frac{I/Y}{C/Y} \\ & = & \frac{6\%}{12}\\ & = & 0.5\%\end{eqnarray*}[/latex]
Step 3: Calculate the number of payments.
[latex]\begin{eqnarray*} n & = & P/Y \times t \\ & = & 12 \times 2 \\ & = & 24 \end{eqnarray*}[/latex]
Step 4: Calculate the present value.
[latex]\begin{eqnarray*} PV & = & PMT \times (1+i_2) \times \left[1-\frac{(1+i_2)^{-n}}{i_2}\right] \\ & = & 250 \times \left[ \frac{1-(1+0.005)^{-24}}{0.005}\right] \\ & = & \$5,668.92 \end{eqnarray*}[/latex]
Step 5: Calculate the interest earned.
[latex]\begin{eqnarray*} I & = & n \times PMT-PV \\ & = & 24 \times 250-5,668.92 \\ & = & \$331.08 \end{eqnarray*}[/latex]
Step 6: Write as a statement.
Tom needs [latex]\$5,668.92[/latex] in his account to receive the [latex]24[/latex] payments of [latex]\$250[/latex]. He will receive [latex]\$331.08[/latex] in interest.
Using a Financial Calculator
The above examples were fairly straightforward annuity questions. But even these simple examples, which did not require interest conversions, are cumbersome, and time-consuming, to solve using the formulas. A financial calculator can quickly solve annuity problems, with the added bonus of not requiring an interest conversion in situations where the payment frequency and compounding frequency are not equal.
Using the TI BAII Plus Calculator to Find the Present Value for Annuities
- Set the calculator to the correct payment setting (END or BGN).
- Enter values for the known variables ([latex]FV[/latex], [latex]PMT[/latex], [latex]N[/latex], [latex]I/Y[/latex], [latex]P/Y[/latex] and [latex]C/Y[/latex]), paying close attention to the cash flow sign convention for [latex]PMT[/latex] and [latex]FV[/latex].
- After all of the known quantities are loaded into the calculator, press [latex]CPT[/latex] and then [latex]PV[/latex] to solve for the present value.
Notes
- Ensure that the calculator is set to the required payment setting. The present value will be different for END and BGN.
- Because you can enter [latex]P/Y[/latex] and [latex]C/Y[/latex], there is no need to do an interest conversion for a general annuity. You simply have to tell the calculator the [latex]P/Y[/latex] and [latex]C/Y[/latex] given in the question, and the calculator will handle any interest conversion internally.
- If there is no money in the account or investment at the end of the term then [latex]FV=0[/latex].
- The values you enter for [latex]PV[/latex], [latex]FV[/latex], and [latex]PMT[/latex] must adhere to the cash flow sign convention.
Ordinary Annuity Calculations (PV, PMT, FV) by Joshua Emmanuel [4:31] (transcript available).
Annuity Due Calculations Using BAII Plus-Part 2 by Joshua Emmanuel [2:05] (transcript available).
Example 2.3.3
Rodriguez is planning on having an annual gross income of [latex]\$50,000[/latex] at the end of every year when he retires at age [latex]65[/latex]. He is planning for the account to be emptied by age [latex]78[/latex], which is the average life expectancy for a Canadian man. If the account earns [latex]5.1\%[/latex] compounded annually, how much money needs to be in the account when he retires?
Solution

The timeline for the Rodriguez's account appears below.
| PMT Setting | END |
| [latex]N[/latex] | [latex]1 \times 13=13[/latex] |
| [latex]PV[/latex] | ? |
| [latex]FV[/latex] | [latex]0[/latex] |
| [latex]PMT[/latex] | [latex]50,000[/latex] |
| [latex]I/Y[/latex] | [latex]5.1[/latex] |
| [latex]P/Y[/latex] | [latex]1[/latex] |
| [latex]C/Y[/latex] | [latex]1[/latex] |
[latex]PV=\$466,863.69[/latex]
Rodriguez will need to have [latex]\$466,863.69[/latex] in his account when he turns [latex]65[/latex] if he wants to receive [latex]13[/latex] years of [latex]\$50,000[/latex] payments.
Try It
1) When Sinbad retires, he expects his RRSP to pay him [latex]\$2,000[/latex] at the end of every month for [latex]25[/latex] years. If his retirement annuity earns [latex]3.8\%[/latex] compounded quarterly, how much money does he need to have in his RRSP when he retires? How much interest will he receive from the RRSP?
Solution
| PMT Setting | END |
| [latex]N[/latex] | [latex]300[/latex] |
| [latex]PV[/latex] | ? |
| [latex]FV[/latex] | [latex]0[/latex] |
| [latex]PMT[/latex] | [latex]2,000[/latex] |
| [latex]I/Y[/latex] | [latex]3.8[/latex] |
| [latex]P/Y[/latex] | [latex]12[/latex] |
| [latex]C/Y[/latex] | [latex]4[/latex] |
[latex]\begin{eqnarray*}PV&=&\$387,444.19\\\\ I & = & n \times PMT-PV \\ & = & 300 \times 2,000-387,444.19 \\ & = & \$212,555.81 \end{eqnarray*}[/latex]
When you purchase an expensive or large-ticket item such as a car or house, you often need to take out a loan to make the purchase. After all, most people do not have large sums of cash available to pay for these items outright. With these expensive items, you often make an up-front partial payment on the purchase price called a down payment, and then take out a loan for the outstanding purchase price.
For example, suppose you want to purchase a [latex]\$100,000[/latex] luxury sports car. You pay [latex]\$10,000[/latex] as a down payment and take out a loan for the balance. The [latex]\$10,000[/latex] down payment is cash you are paying up-front on the purchase price. You would then need to take out a loan for the remaining [latex]\$90,000[/latex] of the purchase price. The [latex]\$90,000[/latex] is a loan, so you would be charged interest for borrowing the money and then you would need to make regularly scheduled payments to pay back the loan. Because the [latex]\$10,000[/latex] down payment is paid up-front, there is no interest charged on this [latex]\$10,000[/latex]. By making the [latex]\$10,000[/latex] down payment, you are reducing the amount of money you need to borrow, and consequently reducing the amount of interest you need to pay.
In general
[latex]\displaystyle{\mbox{Purchase Price}=\mbox{Down Payment}+\mbox{Loan Amount}}[/latex]
Example 2.3.4
Charlie purchased a new car. To pay for the car, she made a [latex]\$5,000[/latex] down payment on the purchase price and took out a loan for the balance at an interest rate of [latex]2.9\%[/latex] compounded monthly. Charlie made [latex]\$550[/latex] monthly payments for six years to settle the loan.
- What is the purchase price of the car?
- How much interest did Charlie pay to purchase the car?
Solution
Step 1: Calculate the purchase price of the car.
| PMT Setting | END |
| [latex]N[/latex] | [latex]12 \times 6=72[/latex] |
| [latex]PV[/latex] | ? |
| [latex]FV[/latex] | [latex]0[/latex] |
| [latex]PMT[/latex] | [latex]-550[/latex] |
| [latex]I/Y[/latex] | [latex]2.9[/latex] |
| [latex]P/Y[/latex] | [latex]12[/latex] |
| [latex]C/Y[/latex] | [latex]12[/latex] |
[latex]\begin{eqnarray*}PV&=&\$36,306.08\\\\ \mbox{Purchase Price} & = & \mbox{Down Payment}+\mbox{Loan Amount} \\ & = & 5,000+36,306.08 \\ & = & \$41,306.08 \end{eqnarray*}[/latex]
Step 2: Calculate the interest.
Because the [latex]\$5,000[/latex] is paid upfront, there is no interest charged on the down payment. Interest is only charged on the loan amount.
[latex]\begin{eqnarray*} I & = & n \times PMT-PV \\ & = & 72 \times 550-36,306.08 \\ & = & \$3,293.92 \end{eqnarray*}[/latex]
Step 3: Write as a statement.
The purchase price of the car was [latex]\$41,306.08[/latex]. Charlie paid [latex]\$3,293.92[/latex] in interest to purchase the car.
Try It
2) You want to purchase a piece of vacant land on the river so that you can build your dream home when you retire. The bank agrees to lend you the money but you have to make a [latex]\$25,000[/latex] down payment and make payments of [latex]\$800[/latex] every month for ten years. The bank charges you interest at [latex]3.5\%[/latex] compounded semi-annually.
- What is the purchase price of the land?
- How much interest will you pay?
Solution
| PMT Setting | END |
| [latex]N[/latex] | [latex]120[/latex] |
| [latex]PV[/latex] | ? |
| [latex]FV[/latex] | [latex]0[/latex] |
| [latex]PMT[/latex] | [latex]-800[/latex] |
| [latex]I/Y[/latex] | [latex]3.5[/latex] |
| [latex]P/Y[/latex] | [latex]12[/latex] |
| [latex]C/Y[/latex] | [latex]2[/latex] |
[latex]\begin{eqnarray*}PV&=&\$80,998.2\\\\ \mbox{Purchase Price} & = & \mbox{Down Payment}+\mbox{Loan Amount} \\ & = & 25,000+80,998.20 \\ & = & \$105,998.20 \\\\ I & = & n \times PMT-PV \\ & = & 120 \times 800-80,998.20 \\ & = & \$15,001.80 \end{eqnarray*}[/latex]
Example 2.3.5
Rodriguez is planning on having an annual gross income of [latex]\$50,000[/latex] at the beginning of every year when he retires at age [latex]65[/latex]. He wants to leave a [latex]\$100,000[/latex] inheritance for his children, assuming he dies at age [latex]78[/latex]. If the account earns [latex]5.1\%[/latex] compounded semi-annually, how much money needs to be in the account when he retires?
Solution

The timeline for the Rodriguez's account appears below.
| PMT Setting | BGN |
| N | [latex]1 \times 13=13[/latex] |
| PV | ? |
| FV | [latex]100,000[/latex] |
| PMT | [latex]50,000[/latex] |
| I/Y | [latex]5.1[/latex] |
| P/Y | [latex]1[/latex] |
| C/Y | [latex]2[/latex] |
[latex]PV=\$541,027.07[/latex]
Rodriguez will need to have [latex]\$541,027.07[/latex] in his account when he turns [latex]65[/latex] if he wants to receive [latex]13[/latex] years of [latex]\$50,000[/latex] payments and leave a [latex]\$100,000[/latex] inheritance for his children.
Try It
3) Sandy's parents would like to have an annuity pay her [latex]\$500[/latex] at the beginning of every month from September 1, 2012 to April 1, 2017 to help with her university tuition and living expenses. On May 1, 2017, they would like to give her a graduation gift of [latex]\$5,000[/latex]. If the annuity can earn [latex]6.15\%[/latex] compounded quarterly, how much money must be in the account on September 1, 2012? (Use years and months in the calculations.)
Solution
| PMT Setting | BGN |
| [latex]N[/latex] | [latex]56[/latex] |
| [latex]PV[/latex] | ? |
| [latex]FV[/latex] | [latex]5,000[/latex] |
| [latex]PMT[/latex] | [latex]500[/latex] |
| [latex]I/Y[/latex] | [latex]6.15[/latex] |
| [latex]P/Y[/latex] | [latex]12[/latex] |
| [latex]C/Y[/latex] | [latex]4[/latex] |
[latex]PV=\$28,188.42[/latex]
Example 2.3.6
Rodriguez is planning on having an annual gross income of [latex]\$50,000[/latex] at the beginning of every year when he retires at age [latex]65[/latex] until age [latex]71[/latex]. Realizing he needs to make some type of adjustment to his annual gross income to account for the rising cost of living, starting at age [latex]71[/latex] he wants his annual payments to increase to [latex]\$60,000[/latex] until age [latex]78[/latex]. He wants to leave a [latex]\$100,000[/latex] inheritance for his children, assuming he dies at age [latex]78[/latex]. If the account earns [latex]5.1\%[/latex] compounded semi-annually, how much needs to be in the account when he retires?
Solution
The timeline for the Rodriguez's account appears below.
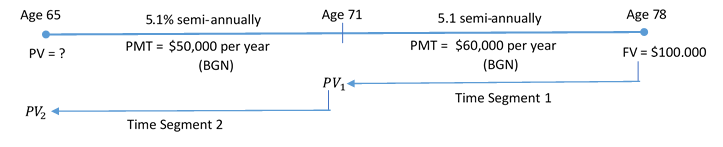
Step 1: Find the present value at the start of time segment [latex]1[/latex].
| PMT Setting | BGN |
| [latex]N[/latex] | [latex]1 \times 7=7[/latex] |
| [latex]PV[/latex] | ? |
| [latex]FV[/latex] | [latex]100,000[/latex] |
| [latex]PMT[/latex] | [latex]60,000[/latex] |
| [latex]I/Y[/latex] | [latex]5.1[/latex] |
| [latex]P/Y[/latex] | [latex]1[/latex] |
| [latex]C/Y[/latex] | [latex]2[/latex] |
[latex]PV_1=\$433,232.035...[/latex]
Step 2: Calculate the present value at the start of time segment [latex]2[/latex].
The present value from time segment [latex]1[/latex] becomes the future value for time segment [latex]2[/latex]: [latex]PV_1=\$433,232.035...=FV_2[/latex].
| PMT Setting | BGN |
| [latex]N[/latex] | [latex]1 \times 6=6[/latex] |
| [latex]PV[/latex] | ? |
| [latex]FV[/latex] | [latex]433,232.035...[/latex] |
| [latex]PMT[/latex] | [latex]50,000[/latex] |
| [latex]I/Y[/latex] | [latex]5.1[/latex] |
| [latex]P/Y[/latex] | [latex]1[/latex] |
| [latex]C/Y[/latex] | [latex]2[/latex] |
[latex]PV_2=\$585,742.42[/latex]
Step 3: Write as a statement.
Rodriguez needs to have [latex]\$585,742.42[/latex] invested in his retirement fund at age [latex]65[/latex].
Try It
4) You want to purchase an annuity that will provide you with payments over the next twelve years. The annuity will pay you [latex]\$1,000[/latex] at the end of every quarter for the first seven years and [latex]\$3,000[/latex] at the end of every six months for the next five years. At the end of the twelve years the annuity is exhausted. If the annuity earns interest at [latex]4.7\%[/latex] compounded monthly, what is the purchase price of the annuity? How much interest does the annuity pay?
Solution
| PMT Setting | END | END |
| [latex]N[/latex] | [latex]10[/latex] | [latex]28[/latex] |
| [latex]PV[/latex] | [latex]\color{blue}{-26,429.159...}[/latex] | [latex]\color{blue}{42,756.53}[/latex] |
| [latex]FV[/latex] | [latex]0[/latex] | [latex]26,429.159...[/latex] |
| [latex]PMT[/latex] | [latex]3,000[/latex] | [latex]1,000[/latex] |
| [latex]I/Y[/latex] | [latex]4.7[/latex] | [latex]4.7[/latex] |
| [latex]P/Y[/latex] | [latex]2[/latex] | [latex]4[/latex] |
| [latex]C/Y[/latex] | [latex]12[/latex] | [latex]12[/latex] |
[latex]\begin{eqnarray*}PV&=&\$42,756.53\\\\ I & = & 10 \times 3,000+28 \times 1,000-42,756.53 \\ & = & \$15,240.47 \end{eqnarray*}[/latex]
Section 2.3 Exercises
- You bought a new luxury sports car for [latex]\$5,000[/latex] down and payments of [latex]\$2,000[/latex] at the beginning of every quarter for [latex]10[/latex] years. If money earns [latex]7\%[/latex] compounded quarterly, what was the purchase price of the car? How much interest did you pay on the loan?
Solution
[latex]\$63,189.28, \$21,810.74[/latex]
- You have an investment that pays you [latex]\$3,000[/latex] every year for [latex]30[/latex] years. How much money must you invest today at [latex]5.6\%[/latex] compounded quarterly?
Solution
[latex]\$42,567.80[/latex]
- You took out a loan that requires you to pay [latex]\$1,500[/latex] every month for [latex]8[/latex] years. How much money did you borrow if the interest on the loan is [latex]8\%[/latex] compounded semi-annually? How much interest did you pay?
Solution
[latex]\$106,605.18, \$37,394.82[/latex]
- Your RIF pays you [latex]\$1,000[/latex] at the end of every quarter for ten years. For the first six years the RIF earns [latex]7\%[/latex] compounded semi-annually and for the last four years the RIF earns [latex]\$6\%[/latex] compounded annually. How much money is in your RIF today? How much interest does the RIF pay?
Solution
[latex]\$28,879.80, \$11,129.20[/latex]
- You want to purchase an annuity that will pay you [latex]\$1,000[/latex] every quarter for the first [latex]10[/latex] years and then [latex]\$750[/latex] every month for the next [latex]5[/latex] years. If the annuity earns [latex]11\%[/latex] compounded quarterly, what is the purchase price of the annuity? How much interest does the annuity pay?
Solution
[latex]\$35,758.83, \$49,241.17[/latex]
- You invest some money into an investment at [latex]10\%[/latex] effective that pays you [latex]\$4,000[/latex] a year for seven years. At the end of the seven years you take the balance in the investment and place it in a savings account at [latex]8\%[/latex] effective and you will withdraw [latex]\$5,000[/latex] a year from the account for three years at which point the account is empty. How much money do you need to invest?
Solution
[latex]\$26,085.97[/latex]
- When Sinbad retires, he expects his RRSP to pay him [latex]\$2,000[/latex] at the end of every month for [latex]25[/latex] years. If his retirement annuity earns [latex]3.8\%[/latex] compounded quarterly, how much money does he need to have in his RRSP when he retires?
Solution
[latex]\$387,444.19[/latex]
- The Workers’ Compensation Board has determined that an injury in the workplace was your company's responsibility. As a result, your company has been ordered to pay the employee [latex]\$3,000[/latex] at the end of every month for the next four years. Your human resource manager wants to set up an annuity to fund this obligation. If the proposed annuity can earn [latex]5.7\%[/latex] compounded monthly for the first two-and-a-half years and then [latex]6\%[/latex] compounded quarterly for the remaining one-and-a half years, how much money should your company set aside today to meet its responsibilities?
Solution
[latex]\$128,398.17[/latex]
- Lynne acquired a Sea Ray Sundancer boat and put [latex]\$4,000[/latex] down. For the past two years, her end-of-month payments have been [latex]\$1,049.01[/latex] including [latex]9.32\%[/latex] compounded monthly. If she still owes [latex]\$22,888.78[/latex] today, what was the purchase price of the boat?
Solution
[latex]\$45,898.34[/latex]
- Gerald has been granted power of attorney and is now responsible for setting up his aging parents in a seniors’ home. The rent will be [latex]\$2,490[/latex] at the beginning of every month for the first year, then increase by [latex]5\%[/latex] the following year and [latex]4\%[/latex] in the third year. Gerald wants to take money from his parents’ estate and set up an annuity to pay their monthly rent. If he can get an annuity that earns [latex]3.75\%[/latex] semi-annually, how much money from his parents’ estate needs to be invested today to meet the rental payments over the next three years?
Solution
[latex]\$88,880.80[/latex]
- Compare the amount of money that needs to be invested today to provide the required payments from the investment
fund annuities earning [latex]9\%[/latex] compounded semi-annually.
- Payments of [latex]\$1,000[/latex] quarterly for [latex]40[/latex] years.
- Payments of [latex]\$1,600[/latex] quarterly for [latex]25[/latex] years.
- Payments of [latex]\$4,000[/latex] quarterly for [latex]10[/latex] years.
Note that in all three of these annuities the same total payout occurs. Explain your results and comment on your findings.
Solution
a. [latex]\$43,610.57[/latex]; b. [latex]\$63,942.03[/latex]; c. [latex]\$105,221.32[/latex]
Attribution
"11.3: Present Value of Annuities" from Business Math: A Step-by-Step Handbook Abridged by Sanja Krajisnik; Carol Leppinen; and Jelena Loncar-Vines is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.
"11.3: Present Value of Annuities" from Business Math: A Step-by-Step Handbook (2021B) by J. Olivier and Lyryx Learning Inc. through a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License unless otherwise noted.

