1.2 Calculating the Future Value
Learning Objectives
- Calculate future value for compound interest
Formula & Symbol Hub
Symbols Used
- [latex]f[/latex] or [latex]EFF[/latex] = Effective interest rate
- [latex]FV[/latex] = Future value or maturity value
- [latex]i[/latex] = Periodic interest rate
- [latex]j[/latex] or [latex]I/Y[/latex] = Nominal interest rate per year
- [latex]m[/latex] or [latex]C/Y[/latex] = Number of compounds per year or compounding frequency
- [latex]n[/latex] or [latex]N[/latex] = Total number of compound periods for the term
- [latex]PV[/latex] = Present value of principal
Formulas Used
-
Formula 1.1 - Total Number of Compounds
[latex]n=m \times \mbox{time in years}[/latex]
-
Formula 1.2 - Periodic Interest Rate
[latex]i=\frac{j}{m}[/latex]
-
Formula 1.3 - Future Value
[latex]FV=PV \times (1+i)^n[/latex]
Introduction
Your company has an employee assistance plan through which employees can borrow funds at [latex]12\%[/latex] compounded semi-annually, much like a loan from a bank, then repay the money at their convenience. An employee who borrowed [latex]\$4,000[/latex] two years ago has been unable to repay the loan until today. As the human resources manager in charge of the assistance plan, you must tell him the exact amount he needs to pay to return his balance to zero. How do you do this?
In the above scenario, you need to tell the employee the future value of their loan. The future value ([latex]FV[/latex])is the accumulated value or maturity value of a loan or an investment at the end of the term of the loan or investment. The future value includes the principal of the loan or investment plus all of the interest the loan or investment has accumulated over the term. The principal of the loan or investment is called the present value ([latex]PV[/latex]). The present value is the amount of money borrowed for a loan or the amount of money invested for an investment at the start of the term.
Calculating the Future Value
Continuing with the scenario described above, suppose [latex]\$4000[/latex] was borrowed two years ago at [latex]12\%[/latex] compounded semi-annually. At the end of the two years, the borrower will owe two years of compound interest in addition to the original principal of [latex]\$4,000[/latex]. The amount of money borrowed for the loan is the present value, so [latex]PV=\$4,000[/latex]. The compounding frequency is semi-annually, or twice per year, which makes the periodic interest rate [latex]i=\frac{j}{m}=\frac{12\%}{2}=6\%[/latex]. This means that every six months, the borrower accumulates [latex]6\%[/latex] of current principal in interest charges. The total number of compoundings is [latex]n=m \times t =2 \times 2=4[/latex], which means that interest will be calculated and added four times over the term of the loan.
At the end of the first six months (one compounding period) of the loan, the current balance or future value of the loan is
[latex]\begin{eqnarray*} \mbox{Balance after first compounding period} & = & \mbox{Principal}+\mbox{Interest} \\ FV & = & PV+ i \times PV \\ & = & 4,000+0.06 \times 4,000 \\ & = & \$4,240 \end{eqnarray*}[/latex]
In the above calculation, note that the equation [latex]FV=PV+i \times PV[/latex] can be factored and rewritten as [latex]FV=PV(1+i)[/latex], which can be used to calculate the future value for each compounding period.
The above process will continue for each of the compounding periods: [latex]6\%[/latex] of the current balance will be added to the balance at the end of each compounding period. For the second compounding period, the present value is the future value from the previous compounding period and the future value is the balance on the loan at the end of the second compounding period.
[latex]\begin{eqnarray*} FV_{\mbox{ after two compounding periods}} & = & PV\times (1+ i ) \\ & = & 4,240\times (1+0.06) \\ & = & \$4,494.40 \end{eqnarray*}[/latex]
Recall that the [latex]PV=\$4,240[/latex] was the result of the future value calculation of the first compounding period. In fact, [latex]4,240=4000 \times (1+0.06)[/latex], which can be substituted into the previous calculation.
[latex]\begin{eqnarray*} FV_{\mbox{ after two compounding periods}} & = & PV\times (1+ i ) \times (1+i) \\ & = & 4,000\times (1+0.06) \times (1+0.06) \\ & = & \$4,494.40 \end{eqnarray*}[/latex]
The equation [latex]FV=PV \times (1+i) \times (1+i)[/latex] can be simplified to the following
[latex]\displaystyle{FV=PV \times (1+i) \times (1+i)=PV \times (1+i)^2}[/latex]
Continuing the calculations for each of the four compounding periods results in the following.
| Compounding Period | Present Value at the Beginning of the Compounding Period | Future Value at the End the Compounding Period |
| [latex]1[/latex] | [latex]\small{\$4,000}[/latex] | [latex]\small{4,000 \times (1+0.06)=\$4,240}[/latex] |
| [latex]2[/latex] | [latex]\small{\$4,240}[/latex] | [latex]\small{\begin{eqnarray*} 4,240 \times (1+0.06) & = & 4,000 \times (1+0.06) \times (1+0.06) \\ & = & 4,000 \times (1+0.06)^2 \\ & = & \$4,494.40 \end{eqnarray*}}[/latex] |
| [latex]3[/latex] | [latex]\small{\$4,494.40}[/latex] | [latex]\small{\begin{eqnarray*} 4,494.40 \times (1+0.06) & = & 4,000 \times (1+0.06) \times (1+0.06) \times (1+0.06) \\ & = & 4,000 \times (1+0.06)^3 \\ & = & \$4,764.06 \end{eqnarray*}}[/latex] |
| [latex]4[/latex] | [latex]\small{\$4,764.06}[/latex] | [latex]\small{\begin{eqnarray*} 4,764.06 \times (1+0.06) & = & 4,000 \times (1+0.06) \times (1+0.06) \times (1+0.06) \times (1+0.06) \\ & = & 4,000 \times (1+0.06)^4 \\ & = & \$5,059.91 \end{eqnarray*}}[/latex] |
Do you notice a pattern in these calculations? With the first compounding period, the formula has only one [latex](1+i)[/latex], with two compounding periods, the formula has two [latex](1+i)[/latex]'s in the form of [latex](1+i)^2[/latex], with three compounding periods, the formula has three [latex](1+i)[/latex]'s in the form [latex](1+i)^3[/latex], and so on. In general, the exponent of [latex](1+i)[/latex] equals the number of the compounding period.
[latex]\boxed{\text{1.3}}[/latex] The Future Value Formula for Compound Interest
[latex]{\color{red}{FV}}\;\text{is the Future Value:}[/latex]the future value includes the principal plus all of the interest accumulated over the term.
[latex]{\color{blue}{PV}}\;\text{is the Present Value or Principal:}[/latex] the present value is the starting amount upon which compound interest is calculated.
[latex]{\color{green}{i}}\;\text{is the Periodic Interest Rate:}[/latex] the periodic interest rate is the interest rate per compounding period: [latex]i=\frac{j}{m}[/latex] where [latex]j[/latex] is the nominal interest rate and [latex]m[/latex] is the compounding frequency.
[latex]{\color{purple}{n}}\;\text{is the Total Number of Compounding Periods Over the Term:}[/latex] [latex]n=m \times t[/latex] where [latex]m[/latex] is the compounding frequency and [latex]t[/latex] is the length of the term in years.
The amount of interest ([latex]I[/latex]) accumulated by a loan or investment is
[latex]\displaystyle{I=FV-PV}[/latex]
Example 1.2.1
If you invested [latex]\$5,000[/latex] for [latex]10[/latex] years at [latex]9\%[/latex] compounded quarterly, how much money would you have? What is the interest earned during the term?
Solution

The timeline for the investment is below.
Step 1: Write what you get from the question.
[latex]\begin{eqnarray*} PV & = & \$5,000 \\ j & = & 9\% \\ m & = & 4 \\ t & = & 10 \mbox{ years} \end{eqnarray*}[/latex]
Step 2: Calculate the periodic interest rate.
[latex]\begin{eqnarray*} i & = & \frac{j}{m} \\ & = & \frac{9\%}{4} \\ & = & 2.25\% \\ & = & 0.0225 \end{eqnarray*}[/latex]
Step 3: Calculate the total number of compoundings.
[latex]\begin{eqnarray*} n & = & m \times t \\ & = & 4 \times 10 \\ & = & 40 \end{eqnarray*}[/latex]
Step 4: Calculate the future value.
[latex]\begin{eqnarray*} FV & = & PV \times (1+i)^n \\ & = & 5,000 \times (1+0.0225)^{40} \\ & = & 5,000 \times (1.0225)^{40} \\ & = & \$12,175.94 \end{eqnarray*}[/latex]
Step 5: Calculate the interest earned.
[latex]\begin{eqnarray*} I & = & FV-PV \\ & = & 12,175.94-5,000 \\ & = & \$7,175.94 \end{eqnarray*}[/latex]
Step 6: Write as a statement.
After [latex]10[/latex] years, the principal grows to [latex]\$12,175.94[/latex], which includes your [latex]\$5,000[/latex] principal and [latex]\$7,175.94[/latex] of interest.
Using a Financial Calculator
A financial calculator, like the TI BAII Plus, has built-in functions to solve compound interest problems. These functions use the "time value of money" buttons on the calculator. Throughout the remainder of this book, we will focus on using the financial calculator to solve problems involving compound interest, instead of using the formulas as illustrated above.
Using the TI BAII Plus Calculator to Find the Future Value for Compound Interest
The time value of money buttons are located in the [latex]TVM[/latex] row (the third row from the top) of the calculator. The five buttons located on the third row of the calculator are five of the seven variables required for time value of money calculations. This row’s buttons are different in color from the rest of the buttons on the keypad. The other two variables are in a secondary menu above the [latex]I/Y[/latex] key and are accessed by pressing 2nd [latex]I/Y[/latex].

Altogether, there are seven variables required to complete time value of money calculations. Note that [latex]P/Y[/latex] and [latex]C/Y[/latex] are not main button keys in the [latex]TVM[/latex] row. The [latex]P/Y[/latex] and [latex]C/Y[/latex] variables are located in the secondary function accessed by pressing 2nd [latex]I/Y[/latex].
| Variable | Meaning |
| [latex]N[/latex] | Total number of compounding periods. This is the same value as [latex]n[/latex] in the future value formula. [latex]N=\mbox{time in years} \times \mbox{compounding frequency}[/latex] |
| [latex]I/Y[/latex] | Interest rate per year (i.e. the nominal interest rate). The interest rate is entered in percent form (without the [latex]\%[/latex] sign). For example, [latex]5\%[/latex] is entered as [latex]5[/latex]. |
| [latex]PV[/latex] | Present value or principal. |
| [latex]PMT[/latex] | Periodic annuity payment. For compound interest only calculations, [latex]PMT=0[/latex]. (Note: in later chapters you will learn about annuities where [latex]PMT[/latex] will not be [latex]0[/latex].) |
| [latex]FV[/latex] | Future value or maturity value. |
| [latex]P/Y[/latex] | Payments frequency for annuity payment. For compound interest only calculations, [latex]P/Y[/latex] is set to the same value as [latex]C/Y[/latex]. (Note: in later chapters you will learn about annuities where [latex]P/Y[/latex] will be set to the frequency of the payments.) |
| [latex]C/Y[/latex] | Compounding frequency. This is the value of [latex]m[/latex]. |
To enter values into the calculator:
- For the main button keys in the [latex]TVM[/latex] row (i.e. [latex]N[/latex], [latex]I/Y[/latex], [latex]PV[/latex], [latex]PMT[/latex], [latex]FV[/latex]), enter the number first and then press the corresponding button.
- For example, to enter [latex]N=34[/latex], enter [latex]34[/latex] on the calculator and then press [latex]N[/latex].
- For [latex]P/Y[/latex] and [latex]C/Y[/latex], press 2nd [latex]I/Y[/latex]. At the [latex]P/Y[/latex] screen, enter the value for [latex]P/Y[/latex] and then press ENTER. Press the down arrow to access the [latex]C/Y[/latex] screen. At the [latex]C/Y[/latex] screen, enter the value for [latex]C/Y[/latex] and then press ENTER. Press 2nd QUIT (the CPT button) to exit the menu.
- For example, to enter [latex]P/Y=4[/latex] and [latex]C/Y=4[/latex], press 2nd [latex]I/Y[/latex]. At the [latex]P/Y[/latex] screen, enter [latex]4[/latex] and press ENTER. Press the down arrow. At the [latex]C/Y[/latex] screen, enter [latex]4[/latex] and press ENTER. Press 2nd QUIT to exit.
After all of the known quantities are loaded into the calculator, press CPT and then [latex]FV[/latex] to solve for the future value.
Notes
- The calculator automatically sets [latex]C/Y[/latex] equal to whatever is entered for [latex]P/Y[/latex]. That is, if you enter [latex]4[/latex] for [latex]P/Y[/latex], the calculator will set [latex]C/Y=4[/latex]. This is what we need to complete compound interest only calculations. When we learn about annuities in later chapters, we will have instances where [latex]P/Y[/latex] and [latex]C/Y[/latex] will need to be different.
- Your calculator has permanent memory. Once you enter data into any of the time value buttons it is permanently stored until
- You override it by entering another piece of data and pressing the button; or
- You clear the memory of the time value buttons by pressing 2nd CLR [latex]TVM[/latex] before proceeding with another question; or
- The reset button on the back of the calculator is pressed.
Video: Compound Interest (Present and Future Values) by Joshua Emmanuel [6:56] (Transcript Available).
Cash Flow Convention Signs
An investment and a loan are very different. An investment earns interest and the principal increases over time. A loan is charged interest but is usually paid off through payments, resulting in the principal decreasing over time. Notice that nowhere on the calculator is there a button to enter this critical piece of information. How does the calculator distinguish between the two? You must apply a principle called the cash flow sign convention to the [latex]PV[/latex], [latex]PMT[/latex], and [latex]FV[/latex] buttons.
- If you have money leaving your possession and going somewhere else (such as being put into an investment or making a payment against a loan), you must enter the number as a NEGATIVE number.
- If you have money coming into your possession and you are receiving it (such as borrowing money from the bank or having an investment mature and pay out to you), you must enter the number as a POSITIVE number.
When doing financial calculations it is important to “be somebody” in the transaction. In any compound interest scenario, two parties are always involved—somebody is investing and somebody is borrowing. From this standpoint, think about whether the money leaves you or comes at you. This will help you place the correct sign in front of the [latex]PV[/latex], [latex]PMT[/latex], and [latex]FV[/latex] when using your calculator. Who you are will not change the numbers of the transaction, just the cash flow sign convention.
- If you borrow money from your friend and then pay it back, the initial loan is received by you and hence entered as a positive [latex]PV[/latex] for you. As you pay back the loan, money leaves you and therefore the [latex]FV[/latex] is negative for you.
- Taking the other side of the coin and being your friend, the loaning of money is a negative [latex]PV[/latex] for him. When you repay the loan, your friend receives it and therefore results in a positive [latex]FV[/latex] for him.
| Sign of FV | Sign of PV | |
| Investments | When you receive your matured investment at the end of the term this is considered as a cash-inflow for you and the future value should be entered as a positive amount. | When money is invested (paid-out), this amount is considered as a cash-outflow and this amount has to be entered as a negative number for [latex]PV[/latex]. |
| Loans | When the loan is repaid at the end of the term this is considered as a cash-outflow for you and the future value should be entered as a negative amount. | When money is received (loaned), this amount is considered as a cash-inflow and this amount has to be entered as a positive number for [latex]PV[/latex]. |
Things to Watch Out For
Notice that the [latex]PV[/latex] and [latex]FV[/latex] always have opposite signs.
When you compute solutions on the BAII Plus calculator, one of the most common error messages displayed is "Error 5." This error indicates that the cash flow sign convention has been used in a manner that is financially impossible. Some examples of these financial impossibilities include loans with no repayment or investments that never pay out. In these cases, the [latex]PV[/latex] and [latex]FV[/latex] have been incorrectly set to the same cash flow sign.
Example 1.2.2
If you invested [latex]\$5,000[/latex] for [latex]10[/latex] years at [latex]9\%[/latex] compounded quarterly, how much money would you have?
Solution

The timeline for the investment is below.
| [latex]N[/latex] | [latex]4 \times 10=40[/latex] |
| [latex]PV[/latex] | [latex]-5,000[/latex] |
| [latex]FV[/latex] | ? |
| [latex]PMT[/latex] | [latex]0[/latex] |
| [latex]I/Y[/latex] | [latex]9[/latex] |
| [latex]P/Y[/latex] | [latex]4[/latex] |
| [latex]C/Y[/latex] | [latex]4[/latex] |
[latex]FV=\$12,175.94[/latex]
Try It
1) Find the future value if [latex]\$53,000[/latex] is invested at [latex]6\%[/latex] compounded monthly for [latex]4[/latex] years and [latex]3[/latex] months. How much interest did the investment make?
Solution
| [latex]N[/latex] | [latex]12 \times \frac{51}{12}=51[/latex] |
| [latex]PV[/latex] | [latex]-53,000[/latex] |
| [latex]FV[/latex] | ? |
| [latex]PMT[/latex] | [latex]0[/latex] |
| [latex]I/Y[/latex] | [latex]6[/latex] |
| [latex]P/Y[/latex] | [latex]12[/latex] |
| [latex]C/Y[/latex] | [latex]12[/latex] |
[latex]\begin{eqnarray*}FV&=&\$68,351.02\\\\ I & = & FV-PV \\ & = & 68,351.02-53,000 \\ & = & \$15,351.02 \end{eqnarray*}[/latex]
Future Value Calculations with Variable Changes
What happens if a variable such as the nominal interest rate, compounding frequency, or even the principal changes somewhere in the middle of the transaction? When any variable changes, you must break the timeline into separate time fragments at the point of the change. To arrive at the solution, you need to work from left to right one time segment at a time using the future value formula.
-
- Read and understand the problem. Identify the present value. Draw a timeline broken into separate time segments at the point of any change. For each time segment, identify any principal changes, the nominal interest rate, the compounding frequency, and the length of the time segment in years.
- Starting with the present value in the first time segment (starting on the left), solve for the future value.
- Let the future value calculated in the previous step become the present value for the next step. If the principal changes, adjust the new present value accordingly.
- Calculate the future value of the next time segment.
- Repeat the previous steps until you obtain the final future value from the final time segment.
HOW TO
Transforming the future value from one time segment into the present value of the next time segment does not require re-entering the computed value. Instead, apply the following technique.
- Load the calculator with all known compound interest variables for the first time segment.
- Compute the future value at the end of the segment.
- With the answer still on your display, adjust the principal if needed, change the cash flow sign by pressing the [latex]\pm[/latex] key, and then store the unrounded number back into the present value button by pressing [latex]PV[/latex]. Change the [latex]N[/latex], [latex]I/Y[/latex], and [latex]C/Y[/latex] as required for the next segment.
- Return to step [latex]2[/latex] for each time segment until you have completed all time segments.
Example 1.2.3
Five years ago Coast Appliances was supposed to upgrade one of its facilities at a quoted cost of [latex]\$48,000[/latex]. The upgrade was not completed, so Coast Appliances delayed the purchase until now. The construction company that provided the quote indicates that prices rose [latex]6\%[/latex] compounded quarterly for the first [latex]1.5[/latex] years, [latex]7\%[/latex] compounded semi-annually for the following [latex]2.5[/latex] years, and [latex]7.5\%[/latex] compounded monthly for the final year. If Coast Appliances wants to perform the upgrade today, what amount of money does it need?
Solution
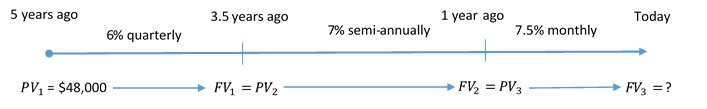
The timeline below shows the original quote from five years ago until today.
Step 1: Calculate the future value at the end of the first segment.
| [latex]N[/latex] | [latex]4 \times 1.5=6[/latex] |
| [latex]PV[/latex] | [latex]-48,000[/latex] |
| [latex]FV[/latex] | ? |
| [latex]PMT[/latex] | [latex]0[/latex] |
| [latex]I/Y[/latex] | [latex]6[/latex] |
| [latex]P/Y[/latex] | [latex]4[/latex] |
| [latex]C/Y[/latex] | [latex]4[/latex] |
[latex]\displaystyle{FV_1=\$52,485.27667....}[/latex]
Step 2: Calculate the future value at the end of the second segment. The future value from the first segment becomes the present value for the second segment: [latex]FV_1=\$52,485.27667....=PV_2[/latex].
| [latex]N[/latex] | [latex]2 \times 2.5=5[/latex] |
| [latex]PV[/latex] | [latex]-52,485.27667...[/latex] |
| [latex]FV[/latex] | ? |
| [latex]PMT[/latex] | [latex]0[/latex] |
| [latex]I/Y[/latex] | [latex]7[/latex] |
| [latex]P/Y[/latex] | [latex]2[/latex] |
| [latex]C/Y[/latex] | [latex]2[/latex] |
[latex]\displaystyle{FV_2=\$62,336.04435....}[/latex]
Step 3: Calculate the future value at the end of the third segment. The future value from the second segment becomes the present value for the third segment: [latex]FV_2=\$62,336.04435....=PV_3[/latex].
| [latex]N[/latex] | [latex]12 \times 1=12[/latex] |
| [latex]PV[/latex] | [latex]-62,336.04435...[/latex] |
| [latex]FV[/latex] | ? |
| [latex]PMT[/latex] | [latex]0[/latex] |
| [latex]I/Y[/latex] | [latex]7.5[/latex] |
| [latex]P/Y[/latex] | [latex]12[/latex] |
| [latex]C/Y[/latex] | [latex]12[/latex] |
[latex]\displaystyle{FV_3=\$67,175.35}[/latex]
Step 4: Write as a statement.
Coast Appliance requires [latex]\$67,175.35[/latex] to perform the upgrade today.
Example 1.2.4
Two years ago Lorelei placed [latex]\$2,000[/latex] into an investment earning [latex]6\%[/latex] compounded monthly. Today she makes a deposit to the investment in the amount of [latex]\$1,500[/latex]. What is the maturity value of her investment three years from now?
Solution
The timeline for the investment is below.

Step 1: Calculate the future value at the end of the first segment.
| [latex]N[/latex] | [latex]12 \times 2=24[/latex] |
| [latex]PV[/latex] | [latex]-2,000[/latex] |
| [latex]FV[/latex] | ? |
| [latex]PMT[/latex] | [latex]0[/latex] |
| [latex]I/Y[/latex] | [latex]6[/latex] |
| [latex]P/Y[/latex] | [latex]12[/latex] |
| [latex]C/Y[/latex] | [latex]12[/latex] |
[latex]\displaystyle{FV_1=\$2,254.31955....}[/latex]
Step 2: Add the [latex]\$1,500[/latex] deposit to [latex]FV_1[/latex] to get the present value for the second segment.
[latex]\displaystyle{PV_2=2,254.31955...+1,500=\$3,754.31955...}[/latex]
Step 3: Calculate the future value at the end of the second segment.
| [latex]N[/latex] | [latex]12 \times 3=36[/latex] |
| [latex]PV[/latex] | [latex]-3,754.31955...[/latex] |
| [latex]FV[/latex] | ? |
| [latex]PMT[/latex] | [latex]0[/latex] |
| [latex]I/Y[/latex] | [latex]6[/latex] |
| [latex]P/Y[/latex] | [latex]12[/latex] |
| [latex]C/Y[/latex] | [latex]12[/latex] |
[latex]\displaystyle{FV_2=\$4,492.72}[/latex]
Step 4: Write as a statement.
Three years from now Lorelei will have [latex]\$4,492.72[/latex]. This represents [latex]\$3,500[/latex] of principal and [latex]\$992.72[/latex] of compound interest.
Try It
2) Find the future value if [latex]\$24,500[/latex] is invested at [latex]4.1\%[/latex] compounded annually for [latex]4[/latex] years; then [latex]5.15\%[/latex] compounded quarterly for [latex]1[/latex] year, [latex]9[/latex] months; then [latex]5.35\%[/latex] compounded monthly for [latex]1[/latex] year, [latex]3[/latex] months.
Solution
| N | [latex]4[/latex] | [latex]7[/latex] | [latex]15[/latex] |
| [latex]PV[/latex] | [latex]-24,500[/latex] | [latex]-28,771.930...[/latex] | [latex]-31,467.335...[/latex] |
| [latex]FV[/latex] | [latex]\color{blue}{28,771.930...}[/latex] | [latex]\color{blue}{31,467.335...}[/latex] | [latex]\color{blue}{33,638.67}[/latex] |
| [latex]PMT[/latex] | [latex]0[/latex] | [latex]0[/latex] | [latex]0[/latex] |
| [latex]I/Y[/latex] | [latex]4.1[/latex] | [latex]5.15[/latex] | [latex]5.35[/latex] |
| [latex]P/Y[/latex] | [latex]1[/latex] | [latex]4[/latex] | [latex]12[/latex] |
| [latex]C/Y[/latex] | [latex]1[/latex] | [latex]4[/latex] | [latex]12[/latex] |
[latex]\displaystyle{FV=\$33,638.67}[/latex]
Try It
3) Nirdosh borrowed [latex]\$9,300 4.25[/latex] years ago at [latex]6.35\%[/latex] compounded semi-annually. The interest rate changed to [latex]6.5\%[/latex] compounded quarterly [latex]1.75[/latex] years ago. What amount of money today is required to pay off this loan?
Solution
| N | [latex]5[/latex] | [latex]7[/latex] |
| [latex]PV[/latex] | [latex]9,300[/latex] | [latex]10,873.1489...[/latex] |
| [latex]FV[/latex] | [latex]\color{blue}{-10,873.1489...}[/latex] | [latex]\color{blue}{12,171.92}[/latex] |
| [latex]PMT[/latex] | [latex]0[/latex] | [latex]0[/latex] |
| [latex]I/Y[/latex] | [latex]6.35[/latex] | [latex]6.5[/latex] |
| [latex]P/Y[/latex] | [latex]2[/latex] | [latex]4[/latex] |
| [latex]C/Y[/latex] | [latex]2[/latex] | [latex]4[/latex] |
[latex]\displaystyle{FV=\$12,171.92}[/latex]
Section 1.2 Exercises
- What is the future value of a [latex]\$7,500[/latex] investment at [latex]8\%[/latex] compounded quarterly for [latex]3[/latex] years?
Solution
[latex]\$9,511.81[/latex]
- Ruth borrowed [latex]\$53,000[/latex] at [latex]6\%[/latex] compounded quarterly [latex]4[/latex] years and [latex]3[/latex] months ago. How much does Ruth have to pay today to clear the loan? How much interest did Ruth pay?
Solution
[latex]FV=\$68,351.02[/latex], [latex]I=\$15,351.02[/latex]
- You invest [latex]\$19,000[/latex] in a savings account at [latex]5.75\%[/latex] compounded semi-annually. How much is in your account [latex]6.5[/latex] years from now?
Solution
[latex]\$27,465.13[/latex]
- You invest [latex]\$3,750[/latex] in an investment that earns [latex]4.75\%[/latex] compounded annually for the first three years and then [latex]5.5\%[/latex] compounded semi-annually for the next two years. How much money do you have at the end of the five years? How much interest did your investment earn?
Solution
[latex]FV=\$4,804.20[/latex], [latex]I=\$1,054.20[/latex]
- James took out a [latex]\$11,375[/latex] loan today. He will pay interest at [latex]7.5\%[/latex] compounded monthly for the first two years and nine months, and then [latex]8.25\%[/latex] compounded quarterly for the next three years and three months. How much money does James owe six years from now?
Solution
[latex]\$18,218.24[/latex]
- You are planning a [latex]16-[/latex]day African safari to Rwanda to catch a rare glimpse of the [latex]700[/latex] remaining mountain gorillas in the world. The estimated cost of this once-in-a-lifetime safari is [latex]\$15,000[/latex] including the tour, permits, lodging, and airfare. Upon your graduation from college, your parents have promised you a [latex]\$10,000[/latex] graduation gift. You intend to save this money for five years in a long-term investment earning [latex]8.3\%[/latex] compounded semi-annually. If the cost of the trip will be about the same, will you have enough money five years from now to pay for your trip?
Solution
[latex]\$15,017.33[/latex]; yes
- Your investment of [latex]\$9,000[/latex] that you started six years ago earned [latex]7.3\%[/latex] compounded quarterly for the first [latex]3\frac{1}{4}[/latex] years, followed by [latex]8.2\%[/latex] compounded monthly after that. How much interest has your investment earned so far?
Solution
[latex]\$5,254.44[/latex]
- What is the maturity value of your [latex]\$7,800[/latex] investment after three years if the interest rate was [latex]5\%[/latex] compounded semiannually for the first two years, [latex]6\%[/latex] compounded quarterly for the last year, and [latex]2\frac{1}{2}[/latex] years after the initial investment you made a deposit of [latex]\$1,200[/latex]? How much interest is earned?
Solution
[latex]FV=\$10,374.33[/latex], [latex]I=\$1,374.33[/latex]
- Cristy borrowed [latex]\$4,800[/latex] from a family friend [latex]2\frac{1}{2}[/latex] years ago at [latex]7\%[/latex] compounded annually for the first year and [latex]8\%[/latex] compounded semi-annually thereafter. She made a payment [latex]1\frac{1}{2}[/latex] years into the loan for [latex]\$2,500[/latex]. How much should Cristy pay today to clear her loan?
Solution
[latex]\$3,073.30[/latex]
- You invested [latex]\$5,000 10[/latex] years ago and made two further deposits of [latex]\$5,000[/latex] each after four years and eight years. Your investment earned [latex]9.2\%[/latex] compounded quarterly for the first two years, [latex]8.75\%[/latex] compounded monthly for the next six years, and [latex]9.8\%[/latex] compounded semi-annually for the remaining years. As of today, how much interest has your investment earned?
Solution
[latex]\$11,888.46[/latex]
- Suppose you placed [latex]\$10,000[/latex] into each of the following investments. Rank the maturity values after five years from highest to lowest.
- [latex]8\%[/latex] compounded annually for two years followed by [latex]6\%[/latex] compounded semi-annually.
- [latex]8\%[/latex] compounded semi-annually for two years followed by [latex]6\%[/latex] compounded annually.
- [latex]8\%[/latex] compounded monthly for two years followed by [latex]6\%[/latex] compounded quarterly.
- [latex]8\%[/latex] compounded semi-annually for two years followed by [latex]6\%[/latex] compounded monthly.
Solution
c is largest with [latex]FV=\$14,023.26[/latex], d is second largest with [latex]FV=\$13,999.47[/latex], b is third largest with [latex]FV=\$13,933.20[/latex], a is smallest with [latex]FV=\$13,927.43[/latex]
- You made the following three investments:
- [latex]\$8,000[/latex] into a five-year fixed rate investment earning [latex]5.65\%[/latex] compounded quarterly.
- [latex]\$6,500[/latex] into a five-year variable rate investment earning [latex]4.83\%[/latex] compounded semi-annually for the first [latex]2\frac{1}{2}[/latex] years and [latex]6.5\%[/latex] compounded monthly for the remainder.
- [latex]\$4,000[/latex] into a five-year variable rate investment earning [latex]4.75\%[/latex] compounded monthly for the first two years and [latex]5.9\%[/latex] compounded quarterly thereafter, with a [latex]\$4,000[/latex] deposit made [latex]21[/latex] months into the investment.
What is the total maturity value of all three investments after the five years, and how much interest is earned?
Solution
[latex]\$29,270.56, \$6,770.56[/latex]
Attribution
“9.2: Determining the Future (Maturity) Value” from Business Math: A Step-by-Step Handbook Abridged by Sanja Krajisnik; Carol Leppinen; and Jelena Loncar-Vinesis licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.
"9.2: Determining the Future Value" from Business Math: A Step-by-Step Handbook (2021B) by J. Olivier and Lyryx Learning Inc. through a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License unless otherwise noted.

