Ordinary Annuity – Changing the Rate

Example

Grace is looking to make some changes to her personal financing. She would like to be able to help her children finance their education. She anticipates that she can save $600 every six months for the next 16 years, at which point her oldest child will be ready for post-secondary education. She estimates that the rate of return will be 3.5% compounded semiannually for the first 5 \frac{1}{2} years. She expects that the interest rate will then increase to 5% compounded for the next 10 \frac{1}{2} years. What is the future value of this simple ordinary annuity?

Begin with a timeline:

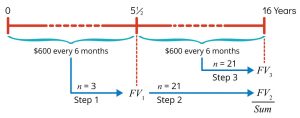
The timeline stretches from 0 to 16 years. The timeline is broken into two parts, at the point where the interest rate changes: 0 to 5.5 years and 5.5 to 16 years, as the interest rate changes at 5.5 years. The number of payments in the first part is n = 11 . We find the corresponding future value, FV1.

In this case, we can use Excel to solve the problem. We have two steps.

Step 1

Calculate the Future Value FV1 of the first 5 \frac{1}{2} years (11 payments).

Step 2

Since the FV from step 1 will continue to earn interest, we use the FV1  as the PV for for the remaining 10 \frac{1}{2} years (21 payments).  Using this PV and new rate, we can calculate the final FV.

See the full solution here: FV of ordinary annuity – changing the rate – Template

License

Icon for the Creative Commons Attribution-NonCommercial 4.0 International License

Using Excel in Business Math Copyright © by Lisa Koster is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License, except where otherwise noted.

Share This Book