39 Non-Equivalent Groups Designs
Learning Objectives
- Describe the different types of nonequivalent groups quasi-experimental designs.
- Identify some of the threats to internal validity associated with each of these designs.
Recall that when participants in a between-subjects experiment are randomly assigned to conditions, the resulting groups are likely to be quite similar. In fact, researchers consider them to be equivalent. When participants are not randomly assigned to conditions, however, the resulting groups are likely to be dissimilar in some ways. For this reason, researchers consider them to be nonequivalent. A nonequivalent groups design, then, is a between-subjects design in which participants have not been randomly assigned to conditions. There are several types of nonequivalent groups designs we will consider.
Posttest Only Nonequivalent Groups Design
The first nonequivalent groups design we will consider is the posttest only nonequivalent groups design. In this design, participants in one group are exposed to a treatment, a nonequivalent group is not exposed to the treatment, and then the two groups are compared. Imagine, for example, a researcher who wants to evaluate a new method of teaching fractions to third graders. One way would be to conduct a study with a treatment group consisting of one class of third-grade students and a control group consisting of another class of third-grade students. This design would be a nonequivalent groups design because the students are not randomly assigned to classes by the researcher, which means there could be important differences between them. For example, the parents of higher achieving or more motivated students might have been more likely to request that their children be assigned to Ms. Williams’s class. Or the principal might have assigned the “troublemakers” to Mr. Jones’s class because he is a stronger disciplinarian. Of course, the teachers’ styles, and even the classroom environments might be very different and might cause different levels of achievement or motivation among the students. If at the end of the study there was a difference in the two classes’ knowledge of fractions, it might have been caused by the difference between the teaching methods—but it might have been caused by any of these confounding variables.
Of course, researchers using a posttest only nonequivalent groups design can take steps to ensure that their groups are as similar as possible. In the present example, the researcher could try to select two classes at the same school, where the students in the two classes have similar scores on a standardized math test and the teachers are the same sex, are close in age, and have similar teaching styles. Taking such steps would increase the internal validity of the study because it would eliminate some of the most important confounding variables. But without true random assignment of the students to conditions, there remains the possibility of other important confounding variables that the researcher was not able to control.
Pretest-Posttest Nonequivalent Groups Design
Another way to improve upon the posttest only nonequivalent groups design is to add a pretest. In the pretest-posttest nonequivalent groups design there is a treatment group that is given a pretest, receives a treatment, and then is given a posttest. But at the same time there is a nonequivalent control group that is given a pretest, does not receive the treatment, and then is given a posttest. The question, then, is not simply whether participants who receive the treatment improve, but whether they improve more than participants who do not receive the treatment.
Imagine, for example, that students in one school are given a pretest on their attitudes toward drugs, then are exposed to an anti-drug program, and finally, are given a posttest. Students in a similar school are given the pretest, not exposed to an anti-drug program, and finally, are given a posttest. Again, if students in the treatment condition become more negative toward drugs, this change in attitude could be an effect of the treatment, but it could also be a matter of history or maturation. If it really is an effect of the treatment, then students in the treatment condition should become more negative than students in the control condition. But if it is a matter of history (e.g., news of a celebrity drug overdose) or maturation (e.g., improved reasoning), then students in the two conditions would be likely to show similar amounts of change. This type of design does not completely eliminate the possibility of confounding variables, however. Something could occur at one of the schools but not the other (e.g., a student drug overdose), so students at the first school would be affected by it while students at the other school would not.
Returning to the example of evaluating a new measure of teaching third graders, this study could be improved by adding a pretest of students’ knowledge of fractions. The changes in scores from pretest to posttest would then be evaluated and compared across conditions to determine whether one group demonstrated a bigger improvement in knowledge of fractions than another. Of course, the teachers’ styles, and even the classroom environments might still be very different and might cause different levels of achievement or motivation among the students that are independent of the teaching intervention. Once again, differential history also represents a potential threat to internal validity. If asbestos is found in one of the schools causing it to be shut down for a month then this interruption in teaching could produce a difference across groups on posttest scores.
If participants in this kind of design are randomly assigned to conditions, it becomes a true between-groups experiment rather than a quasi-experiment. In fact, it is the kind of experiment that Eysenck called for—and that has now been conducted many times—to demonstrate the effectiveness of psychotherapy.
Interrupted Time-Series Design with Nonequivalent Groups
One way to improve upon the interrupted time-series design is to add a control group. The interrupted time-series design with nonequivalent groups involves taking a set of measurements at intervals over a period of time both before and after an intervention of interest in two or more nonequivalent groups. Once again consider the manufacturing company that measures its workers’ productivity each week for a year before and after reducing work shifts from 10 hours to 8 hours. This design could be improved by locating another manufacturing company who does not plan to change their shift length and using them as a nonequivalent control group. If productivity increased rather quickly after the shortening of the work shifts in the treatment group but productivity remained consistent in the control group, then this provides better evidence for the effectiveness of the treatment.
Similarly, in the example of examining the effects of taking attendance on student absences in a research methods course, the design could be improved by using students in another section of the research methods course as a control group. If a consistently higher number of absences was found in the treatment group before the intervention, followed by a sustained drop in absences after the treatment, while the nonequivalent control group showed consistently high absences across the semester then this would provide superior evidence for the effectiveness of the treatment in reducing absences.
Pretest-Posttest Design With Switching Replication
Some of these nonequivalent control group designs can be further improved by adding a switching replication. Using a pretest-posttest design with switching replication design, nonequivalent groups are administered a pretest of the dependent variable, then one group receives a treatment while a nonequivalent control group does not receive a treatment, the dependent variable is assessed again, and then the treatment is added to the control group, and finally the dependent variable is assessed one last time.
As a concrete example, let’s say we wanted to introduce an exercise intervention for the treatment of depression. We recruit one group of patients experiencing depression and a nonequivalent control group of students experiencing depression. We first measure depression levels in both groups, and then we introduce the exercise intervention to the patients experiencing depression, but we hold off on introducing the treatment to the students. We then measure depression levels in both groups. If the treatment is effective we should see a reduction in the depression levels of the patients (who received the treatment) but not in the students (who have not yet received the treatment). Finally, while the group of patients continues to engage in the treatment, we would introduce the treatment to the students with depression. Now and only now should we see the students’ levels of depression decrease.
One of the strengths of this design is that it includes a built in replication. In the example given, we would get evidence for the efficacy of the treatment in two different samples (patients and students). Another strength of this design is that it provides more control over history effects. It becomes rather unlikely that some outside event would perfectly coincide with the introduction of the treatment in the first group and with the delayed introduction of the treatment in the second group. For instance, if a change in the weather occurred when we first introduced the treatment to the patients, and this explained their reductions in depression the second time that depression was measured, then we would see depression levels decrease in both the groups. Similarly, the switching replication helps to control for maturation and instrumentation. Both groups would be expected to show the same rates of spontaneous remission of depression and if the instrument for assessing depression happened to change at some point in the study the change would be consistent across both of the groups. Of course, demand characteristics, placebo effects, and experimenter expectancy effects can still be problems. But they can be controlled for using some of the methods described in Chapter 5.
Switching Replication with Treatment Removal Design
In a basic pretest-posttest design with switching replication, the first group receives a treatment and the second group receives the same treatment a little bit later on (while the initial group continues to receive the treatment). In contrast, in a switching replication with treatment removal design, the treatment is removed from the first group when it is added to the second group. Once again, let’s assume we first measure the depression levels of patients with depression and students with depression. Then we introduce the exercise intervention to only the patients. After they have been exposed to the exercise intervention for a week we assess depression levels again in both groups. If the intervention is effective then we should see depression levels decrease in the patient group but not the student group (because the students haven’t received the treatment yet). Next, we would remove the treatment from the group of patients with depression. So we would tell them to stop exercising. At the same time, we would tell the student group to start exercising. After a week of the students exercising and the patients not exercising, we would reassess depression levels. Now if the intervention is effective we should see that the depression levels have decreased in the student group but that they have increased in the patient group (because they are no longer exercising).
Demonstrating a treatment effect in two groups staggered over time and demonstrating the reversal of the treatment effect after the treatment has been removed can provide strong evidence for the efficacy of the treatment. In addition to providing evidence for the replicability of the findings, this design can also provide evidence for whether the treatment continues to show effects after it has been withdrawn.
{{unknown}}
Learning Objectives
- Define correlational research and give several examples.
- Explain why a researcher might choose to conduct correlational research rather than experimental research or another type of non-experimental research.
- Interpret the strength and direction of different correlation coefficients.
- Explain why correlation does not imply causation.
What Is Correlational Research?
Correlational research is a type of non-experimental research in which the researcher measures two variables (binary or continuous) and assesses the statistical relationship (i.e., the correlation) between them with little or no effort to control extraneous variables. There are many reasons that researchers interested in statistical relationships between variables would choose to conduct a correlational study rather than an experiment. The first is that they do not believe that the statistical relationship is a causal one or are not interested in causal relationships. Recall two goals of science are to describe and to predict and the correlational research strategy allows researchers to achieve both of these goals. Specifically, this strategy can be used to describe the strength and direction of the relationship between two variables and if there is a relationship between the variables then the researchers can use scores on one variable to predict scores on the other (using a statistical technique called regression, which is discussed further in the section on Complex Correlation in this chapter).
Another reason that researchers would choose to use a correlational study rather than an experiment is that the statistical relationship of interest is thought to be causal, but the researcher cannot manipulate the independent variable because it is impossible, impractical, or unethical. For example, while a researcher might be interested in the relationship between the frequency people use cannabis and their memory abilities they cannot ethically manipulate the frequency that people use cannabis. As such, they must rely on the correlational research strategy; they must simply measure the frequency that people use cannabis and measure their memory abilities using a standardized test of memory and then determine whether the frequency people use cannabis is statistically related to memory test performance.
Correlation is also used to establish the reliability and validity of measurements. For example, a researcher might evaluate the validity of a brief extraversion test by administering it to a large group of participants along with a longer extraversion test that has already been shown to be valid. This researcher might then check to see whether participants’ scores on the brief test are strongly correlated with their scores on the longer one. Neither test score is thought to cause the other, so there is no independent variable to manipulate. In fact, the terms independent variable and dependent variable do not apply to this kind of research.
Another strength of correlational research is that it is often higher in external validity than experimental research. Recall there is typically a trade-off between internal validity and external validity. As greater controls are added to experiments, internal validity is increased but often at the expense of external validity as artificial conditions are introduced that do not exist in reality. In contrast, correlational studies typically have low internal validity because nothing is manipulated or controlled but they often have high external validity. Since nothing is manipulated or controlled by the experimenter the results are more likely to reflect relationships that exist in the real world.
Finally, extending upon this trade-off between internal and external validity, correlational research can help to provide converging evidence for a theory. If a theory is supported by a true experiment that is high in internal validity as well as by a correlational study that is high in external validity then the researchers can have more confidence in the validity of their theory. As a concrete example, correlational studies establishing that there is a relationship between watching violent television and aggressive behavior have been complemented by experimental studies confirming that the relationship is a causal one (Bushman & Huesmann, 2001)[1].
Does Correlational Research Always Involve Quantitative Variables?
A common misconception among beginning researchers is that correlational research must involve two quantitative variables, such as scores on two extraversion tests or the number of daily hassles and number of symptoms people have experienced. However, the defining feature of correlational research is that the two variables are measured—neither one is manipulated—and this is true regardless of whether the variables are quantitative or categorical. Imagine, for example, that a researcher administers the Rosenberg Self-Esteem Scale to 50 American college students and 50 Japanese college students. Although this “feels” like a between-subjects experiment, it is a correlational study because the researcher did not manipulate the students’ nationalities. The same is true of the study by Cacioppo and Petty comparing college faculty and factory workers in terms of their need for cognition. It is a correlational study because the researchers did not manipulate the participants’ occupations.
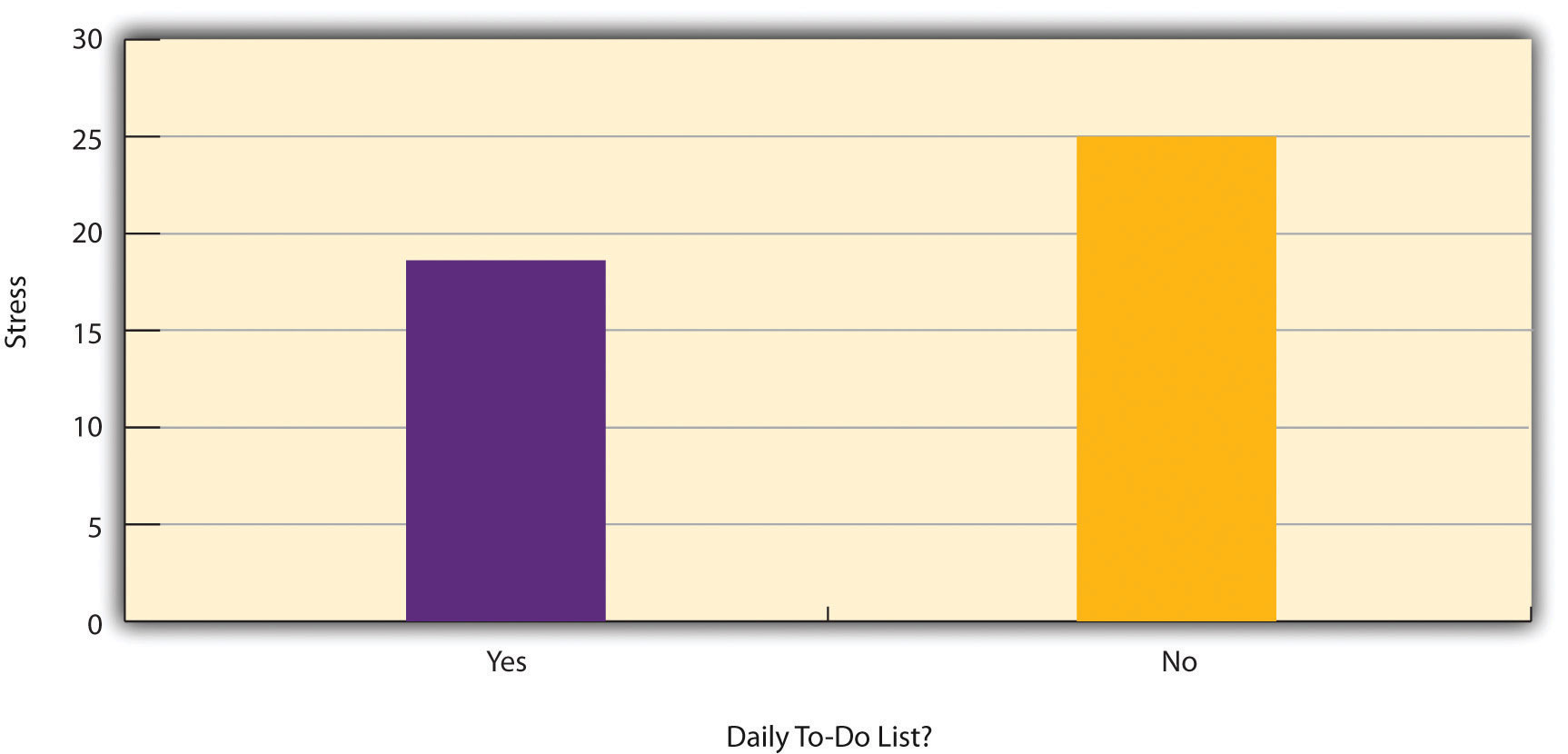
Figure 6.2 shows data from a hypothetical study on the relationship between whether people make a daily list of things to do (a “to-do list”) and stress. Notice that it is unclear whether this is an experiment or a correlational study because it is unclear whether the independent variable was manipulated. If the researcher randomly assigned some participants to make daily to-do lists and others not to, then it is an experiment. If the researcher simply asked participants whether they made daily to-do lists, then it is a correlational study. The distinction is important because if the study was an experiment, then it could be concluded that making the daily to-do lists reduced participants’ stress. But if it was a correlational study, it could only be concluded that these variables are statistically related. Perhaps being stressed has a negative effect on people’s ability to plan ahead (the directionality problem). Or perhaps people who are more conscientious are more likely to make to-do lists and less likely to be stressed (the third-variable problem). The crucial point is that what defines a study as experimental or correlational is not the variables being studied, nor whether the variables are quantitative or categorical, nor the type of graph or statistics used to analyze the data. What defines a study is how the study is conducted.
Data Collection in Correlational Research
Again, the defining feature of correlational research is that neither variable is manipulated. It does not matter how or where the variables are measured. A researcher could have participants come to a laboratory to complete a computerized backward digit span task and a computerized risky decision-making task and then assess the relationship between participants’ scores on the two tasks. Or a researcher could go to a shopping mall to ask people about their attitudes toward the environment and their shopping habits and then assess the relationship between these two variables. Both of these studies would be correlational because no independent variable is manipulated.
Correlations Between Quantitative Variables
Correlations between quantitative variables are often presented using scatterplots. Figure 6.3 shows some hypothetical data on the relationship between the amount of stress people are under and the number of physical symptoms they have. Each point in the scatterplot represents one person’s score on both variables. For example, the circled point in Figure 6.3 represents a person whose stress score was 10 and who had three physical symptoms. Taking all the points into account, one can see that people under more stress tend to have more physical symptoms. This is a good example of a positive relationship, in which higher scores on one variable tend to be associated with higher scores on the other. In other words, they move in the same direction, either both up or both down. A negative relationship is one in which higher scores on one variable tend to be associated with lower scores on the other. In other words, they move in opposite directions. There is a negative relationship between stress and immune system functioning, for example, because higher stress is associated with lower immune system functioning.

The strength of a correlation between quantitative variables is typically measured using a statistic called Pearson’s Correlation Coefficient (or Pearson's r). As Figure 6.4 shows, Pearson’s r ranges from −1.00 (the strongest possible negative relationship) to +1.00 (the strongest possible positive relationship). A value of 0 means there is no relationship between the two variables. When Pearson’s r is 0, the points on a scatterplot form a shapeless “cloud.” As its value moves toward −1.00 or +1.00, the points come closer and closer to falling on a single straight line. Correlation coefficients near ±.10 are considered small, values near ± .30 are considered medium, and values near ±.50 are considered large. Notice that the sign of Pearson’s r is unrelated to its strength. Pearson’s r values of +.30 and −.30, for example, are equally strong; it is just that one represents a moderate positive relationship and the other a moderate negative relationship. With the exception of reliability coefficients, most correlations that we find in Psychology are small or moderate in size. The website http://rpsychologist.com/d3/correlation/, created by Kristoffer Magnusson, provides an excellent interactive visualization of correlations that permits you to adjust the strength and direction of a correlation while witnessing the corresponding changes to the scatterplot.

There are two common situations in which the value of Pearson’s r can be misleading. Pearson’s r is a good measure only for linear relationships, in which the points are best approximated by a straight line. It is not a good measure for nonlinear relationships, in which the points are better approximated by a curved line. Figure 6.5, for example, shows a hypothetical relationship between the amount of sleep people get per night and their level of depression. In this example, the line that best approximates the points is a curve—a kind of upside-down “U”—because people who get about eight hours of sleep tend to be the least depressed. Those who get too little sleep and those who get too much sleep tend to be more depressed. Even though Figure 6.5 shows a fairly strong relationship between depression and sleep, Pearson’s r would be close to zero because the points in the scatterplot are not well fit by a single straight line. This means that it is important to make a scatterplot and confirm that a relationship is approximately linear before using Pearson’s r. Nonlinear relationships are fairly common in psychology, but measuring their strength is beyond the scope of this book.

The other common situations in which the value of Pearson’s r can be misleading is when one or both of the variables have a limited range in the sample relative to the population. This problem is referred to as restriction of range. Assume, for example, that there is a strong negative correlation between people’s age and their enjoyment of hip hop music as shown by the scatterplot in Figure 6.6. Pearson’s r here is −.77. However, if we were to collect data only from 18- to 24-year-olds—represented by the shaded area of Figure 6.6—then the relationship would seem to be quite weak. In fact, Pearson’s r for this restricted range of ages is 0. It is a good idea, therefore, to design studies to avoid restriction of range. For example, if age is one of your primary variables, then you can plan to collect data from people of a wide range of ages. Because restriction of range is not always anticipated or easily avoidable, however, it is good practice to examine your data for possible restriction of range and to interpret Pearson’s r in light of it. (There are also statistical methods to correct Pearson’s r for restriction of range, but they are beyond the scope of this book).

Correlation Does Not Imply Causation
You have probably heard repeatedly that “Correlation does not imply causation.” An amusing example of this comes from a 2012 study that showed a positive correlation (Pearson’s r = 0.79) between the per capita chocolate consumption of a nation and the number of Nobel prizes awarded to citizens of that nation[2]. It seems clear, however, that this does not mean that eating chocolate causes people to win Nobel prizes, and it would not make sense to try to increase the number of Nobel prizes won by recommending that parents feed their children more chocolate.
There are two reasons that correlation does not imply causation. The first is called the directionality problem. Two variables, X and Y, can be statistically related because X causes Y or because Y causes X. Consider, for example, a study showing that whether or not people exercise is statistically related to how happy they are—such that people who exercise are happier on average than people who do not. This statistical relationship is consistent with the idea that exercising causes happiness, but it is also consistent with the idea that happiness causes exercise. Perhaps being happy gives people more energy or leads them to seek opportunities to socialize with others by going to the gym. The second reason that correlation does not imply causation is called the third-variable problem. Two variables, X and Y, can be statistically related not because X causes Y, or because Y causes X, but because some third variable, Z, causes both X and Y. For example, the fact that nations that have won more Nobel prizes tend to have higher chocolate consumption probably reflects geography in that European countries tend to have higher rates of per capita chocolate consumption and invest more in education and technology (once again, per capita) than many other countries in the world. Similarly, the statistical relationship between exercise and happiness could mean that some third variable, such as physical health, causes both of the others. Being physically healthy could cause people to exercise and cause them to be happier. Correlations that are a result of a third-variable are often referred to as spurious correlations.
Some excellent and amusing examples of spurious correlations can be found at http://www.tylervigen.com (Figure 6.7 provides one such example).

“Lots of Candy Could Lead to Violence”
Although researchers in psychology know that correlation does not imply causation, many journalists do not. One website about correlation and causation, http://jonathan.mueller.faculty.noctrl.edu/100/correlation_or_causation.htm, links to dozens of media reports about real biomedical and psychological research. Many of the headlines suggest that a causal relationship has been demonstrated when a careful reading of the articles shows that it has not because of the directionality and third-variable problems.
One such article is about a study showing that children who ate candy every day were more likely than other children to be arrested for a violent offense later in life. But could candy really “lead to” violence, as the headline suggests? What alternative explanations can you think of for this statistical relationship? How could the headline be rewritten so that it is not misleading?
As you have learned by reading this book, there are various ways that researchers address the directionality and third-variable problems. The most effective is to conduct an experiment. For example, instead of simply measuring how much people exercise, a researcher could bring people into a laboratory and randomly assign half of them to run on a treadmill for 15 minutes and the rest to sit on a couch for 15 minutes. Although this seems like a minor change to the research design, it is extremely important. Now if the exercisers end up in more positive moods than those who did not exercise, it cannot be because their moods affected how much they exercised (because it was the researcher who used random assignment to determine how much they exercised). Likewise, it cannot be because some third variable (e.g., physical health) affected both how much they exercised and what mood they were in. Thus experiments eliminate the directionality and third-variable problems and allow researchers to draw firm conclusions about causal relationships.
Learning Objectives
- Explain the purpose of null hypothesis testing, including the role of sampling error.
- Describe the basic logic of null hypothesis testing.
- Describe the role of relationship strength and sample size in determining statistical significance and make reasonable judgments about statistical significance based on these two factors.
The Purpose of Null Hypothesis Testing
As we have seen, psychological research typically involves measuring one or more variables in a sample and computing descriptive summary data (e.g., means, correlation coefficients) for those variables. These descriptive data for the sample are called statistics. In general, however, the researcher’s goal is not to draw conclusions about that sample but to draw conclusions about the population that the sample was selected from. Thus researchers must use sample statistics to draw conclusions about the corresponding values in the population. These corresponding values in the population are called parameters. Imagine, for example, that a researcher measures the number of depressive symptoms exhibited by each of 50 adults with clinical depression and computes the mean number of symptoms. The researcher probably wants to use this sample statistic (the mean number of symptoms for the sample) to draw conclusions about the corresponding population parameter (the mean number of symptoms for adults with clinical depression).
Unfortunately, sample statistics are not perfect estimates of their corresponding population parameters. This is because there is a certain amount of random variability in any statistic from sample to sample. The mean number of depressive symptoms might be 8.73 in one sample of adults with clinical depression, 6.45 in a second sample, and 9.44 in a third—even though these samples are selected randomly from the same population. Similarly, the correlation (Pearson’s r) between two variables might be +.24 in one sample, −.04 in a second sample, and +.15 in a third—again, even though these samples are selected randomly from the same population. This random variability in a statistic from sample to sample is called sampling error. (Note that the term error here refers to random variability and does not imply that anyone has made a mistake. No one “commits a sampling error.”)
One implication of this is that when there is a statistical relationship in a sample, it is not always clear that there is a statistical relationship in the population. A small difference between two group means in a sample might indicate that there is a small difference between the two group means in the population. But it could also be that there is no difference between the means in the population and that the difference in the sample is just a matter of sampling error. Similarly, a Pearson’s r value of −.29 in a sample might mean that there is a negative relationship in the population. But it could also be that there is no relationship in the population and that the relationship in the sample is just a matter of sampling error.
In fact, any statistical relationship in a sample can be interpreted in two ways:
- There is a relationship in the population, and the relationship in the sample reflects this.
- There is no relationship in the population, and the relationship in the sample reflects only sampling error.
The purpose of null hypothesis testing is simply to help researchers decide between these two interpretations.
The Logic of Null Hypothesis Testing
Null hypothesis testing (often called null hypothesis significance testing or NHST) is a formal approach to deciding between two interpretations of a statistical relationship in a sample. One interpretation is called the null hypothesis (often symbolized H0 and read as “H-zero”). This is the idea that there is no relationship in the population and that the relationship in the sample reflects only sampling error. Informally, the null hypothesis is that the sample relationship “occurred by chance.” The other interpretation is called the alternative hypothesis (often symbolized as H1). This is the idea that there is a relationship in the population and that the relationship in the sample reflects this relationship in the population.
Again, every statistical relationship in a sample can be interpreted in either of these two ways: It might have occurred by chance, or it might reflect a relationship in the population. So researchers need a way to decide between them. Although there are many specific null hypothesis testing techniques, they are all based on the same general logic. The steps are as follows:
- Assume for the moment that the null hypothesis is true. There is no relationship between the variables in the population.
- Determine how likely the sample relationship would be if the null hypothesis were true.
- If the sample relationship would be extremely unlikely, then reject the null hypothesis in favor of the alternative hypothesis. If it would not be extremely unlikely, then retain the null hypothesis.
Following this logic, we can begin to understand why Mehl and his colleagues concluded that there is no difference in talkativeness between women and men in the population. In essence, they asked the following question: “If there were no difference in the population, how likely is it that we would find a small difference of d = 0.06 in our sample?” Their answer to this question was that this sample relationship would be fairly likely if the null hypothesis were true. Therefore, they retained the null hypothesis—concluding that there is no evidence of a sex difference in the population. We can also see why Kanner and his colleagues concluded that there is a correlation between hassles and symptoms in the population. They asked, “If the null hypothesis were true, how likely is it that we would find a strong correlation of +.60 in our sample?” Their answer to this question was that this sample relationship would be fairly unlikely if the null hypothesis were true. Therefore, they rejected the null hypothesis in favor of the alternative hypothesis—concluding that there is a positive correlation between these variables in the population.
A crucial step in null hypothesis testing is finding the probability of the sample result or a more extreme result if the null hypothesis were true (Lakens, 2017).[3] This probability is called the p value. A low p value means that the sample or more extreme result would be unlikely if the null hypothesis were true and leads to the rejection of the null hypothesis. A p value that is not low means that the sample or more extreme result would be likely if the null hypothesis were true and leads to the retention of the null hypothesis. But how low must the p value criterion be before the sample result is considered unlikely enough to reject the null hypothesis? In null hypothesis testing, this criterion is called α (alpha) and is almost always set to .05. If there is a 5% chance or less of a result at least as extreme as the sample result if the null hypothesis were true, then the null hypothesis is rejected. When this happens, the result is said to be statistically significant. If there is greater than a 5% chance of a result as extreme as the sample result when the null hypothesis is true, then the null hypothesis is retained. This does not necessarily mean that the researcher accepts the null hypothesis as true—only that there is not currently enough evidence to reject it. Researchers often use the expression “fail to reject the null hypothesis” rather than “retain the null hypothesis,” but they never use the expression “accept the null hypothesis.”
The Misunderstood p Value
The p value is one of the most misunderstood quantities in psychological research (Cohen, 1994)[4]. Even professional researchers misinterpret it, and it is not unusual for such misinterpretations to appear in statistics textbooks!
The most common misinterpretation is that the p value is the probability that the null hypothesis is true—that the sample result occurred by chance. For example, a misguided researcher might say that because the p value is .02, there is only a 2% chance that the result is due to chance and a 98% chance that it reflects a real relationship in the population. But this is incorrect. The p value is really the probability of a result at least as extreme as the sample result if the null hypothesis were true. So a p value of .02 means that if the null hypothesis were true, a sample result this extreme would occur only 2% of the time.
You can avoid this misunderstanding by remembering that the p value is not the probability that any particular hypothesis is true or false. Instead, it is the probability of obtaining the sample result if the null hypothesis were true.

Role of Sample Size and Relationship Strength
Recall that null hypothesis testing involves answering the question, “If the null hypothesis were true, what is the probability of a sample result as extreme as this one?” In other words, “What is the p value?” It can be helpful to see that the answer to this question depends on just two considerations: the strength of the relationship and the size of the sample. Specifically, the stronger the sample relationship and the larger the sample, the less likely the result would be if the null hypothesis were true. That is, the lower the p value. This should make sense. Imagine a study in which a sample of 500 women is compared with a sample of 500 men in terms of some psychological characteristic, and Cohen’s d is a strong 0.50. If there were really no sex difference in the population, then a result this strong based on such a large sample should seem highly unlikely. Now imagine a similar study in which a sample of three women is compared with a sample of three men, and Cohen’s d is a weak 0.10. If there were no sex difference in the population, then a relationship this weak based on such a small sample should seem likely. And this is precisely why the null hypothesis would be rejected in the first example and retained in the second.
Of course, sometimes the result can be weak and the sample large, or the result can be strong and the sample small. In these cases, the two considerations trade off against each other so that a weak result can be statistically significant if the sample is large enough and a strong relationship can be statistically significant even if the sample is small. Table 13.1 shows roughly how relationship strength and sample size combine to determine whether a sample result is statistically significant. The columns of the table represent the three levels of relationship strength: weak, medium, and strong. The rows represent four sample sizes that can be considered small, medium, large, and extra large in the context of psychological research. Thus each cell in the table represents a combination of relationship strength and sample size. If a cell contains the word Yes, then this combination would be statistically significant for both Cohen’s d and Pearson’s r. If it contains the word No, then it would not be statistically significant for either. There is one cell where the decision for d and r would be different and another where it might be different depending on some additional considerations, which are discussed in Section 13.2 "Some Basic Null Hypothesis Tests"
| Relationship strength | |||
| Sample Size | Weak | Medium | Strong |
| Small (N = 20) | No | No | d = Maybe
r = Yes |
| Medium (N = 50) | No | Yes | Yes |
| Large (N = 100) | d = Yes
r = No |
Yes | Yes |
| Extra large (N = 500) | Yes | Yes | Yes |
Although Table 13.1 provides only a rough guideline, it shows very clearly that weak relationships based on medium or small samples are never statistically significant and that strong relationships based on medium or larger samples are always statistically significant. If you keep this lesson in mind, you will often know whether a result is statistically significant based on the descriptive statistics alone. It is extremely useful to be able to develop this kind of intuitive judgment. One reason is that it allows you to develop expectations about how your formal null hypothesis tests are going to come out, which in turn allows you to detect problems in your analyses. For example, if your sample relationship is strong and your sample is medium, then you would expect to reject the null hypothesis. If for some reason your formal null hypothesis test indicates otherwise, then you need to double-check your computations and interpretations. A second reason is that the ability to make this kind of intuitive judgment is an indication that you understand the basic logic of this approach in addition to being able to do the computations.
Statistical Significance Versus Practical Significance
Table 13.1 illustrates another extremely important point. A statistically significant result is not necessarily a strong one. Even a very weak result can be statistically significant if it is based on a large enough sample. This is closely related to Janet Shibley Hyde’s argument about sex differences (Hyde, 2007)[5]. The differences between women and men in mathematical problem solving and leadership ability are statistically significant. But the word significant can cause people to interpret these differences as strong and important—perhaps even important enough to influence the college courses they take or even who they vote for. As we have seen, however, these statistically significant differences are actually quite weak—perhaps even “trivial.”
This is why it is important to distinguish between the statistical significance of a result and the practical significance of that result. Practical significance refers to the importance or usefulness of the result in some real-world context. Many sex differences are statistically significant—and may even be interesting for purely scientific reasons—but they are not practically significant. In clinical practice, this same concept is often referred to as “clinical significance.” For example, a study on a new treatment for social phobia might show that it produces a statistically significant positive effect. Yet this effect still might not be strong enough to justify the time, effort, and other costs of putting it into practice—especially if easier and cheaper treatments that work almost as well already exist. Although statistically significant, this result would be said to lack practical or clinical significance.

Learning Objectives
- List the various types of observational research methods and distinguish between each.
- Describe the strengths and weakness of each observational research method.
What Is Observational Research?
The term observational research is used to refer to several different types of non-experimental studies in which behavior is systematically observed and recorded. The goal of observational research is to describe a variable or set of variables. More generally, the goal is to obtain a snapshot of specific characteristics of an individual, group, or setting. As described previously, observational research is non-experimental because nothing is manipulated or controlled, and as such we cannot arrive at causal conclusions using this approach. The data that are collected in observational research studies are often qualitative in nature but they may also be quantitative or both (mixed-methods). There are several different types of observational methods that will be described below.
Naturalistic Observation
Naturalistic observation is an observational method that involves observing people’s behavior in the environment in which it typically occurs. Thus naturalistic observation is a type of field research (as opposed to a type of laboratory research). Jane Goodall's famous research on chimpanzees is a classic example of naturalistic observation. Dr. Goodall spent three decades observing chimpanzees in their natural environment in East Africa. She examined such things as chimpanzee’s social structure, mating patterns, gender roles, family structure, and care of offspring by observing them in the wild. However, naturalistic observation could more simply involve observing shoppers in a grocery store, children on a school playground, or psychiatric inpatients in their wards. Researchers engaged in naturalistic observation usually make their observations as unobtrusively as possible so that participants are not aware that they are being studied. Such an approach is called disguised naturalistic observation. Ethically, this method is considered to be acceptable if the participants remain anonymous and the behavior occurs in a public setting where people would not normally have an expectation of privacy. Grocery shoppers putting items into their shopping carts, for example, are engaged in public behavior that is easily observable by store employees and other shoppers. For this reason, most researchers would consider it ethically acceptable to observe them for a study. On the other hand, one of the arguments against the ethicality of the naturalistic observation of “bathroom behavior” discussed earlier in the book is that people have a reasonable expectation of privacy even in a public restroom and that this expectation was violated.
In cases where it is not ethical or practical to conduct disguised naturalistic observation, researchers can conduct undisguised naturalistic observation where the participants are made aware of the researcher presence and monitoring of their behavior. However, one concern with undisguised naturalistic observation is reactivity. Reactivity refers to when a measure changes participants’ behavior. In the case of undisguised naturalistic observation, the concern with reactivity is that when people know they are being observed and studied, they may act differently than they normally would. This type of reactivity is known as the Hawthorne effect. For instance, you may act much differently in a bar if you know that someone is observing you and recording your behaviors and this would invalidate the study. So disguised observation is less reactive and therefore can have higher validity because people are not aware that their behaviors are being observed and recorded. However, we now know that people often become used to being observed and with time they begin to behave naturally in the researcher’s presence. In other words, over time people habituate to being observed. Think about reality shows like Big Brother or Survivor where people are constantly being observed and recorded. While they may be on their best behavior at first, in a fairly short amount of time they are flirting, having sex, wearing next to nothing, screaming at each other, and occasionally behaving in ways that are embarrassing.
Participant Observation
Another approach to data collection in observational research is participant observation. In participant observation, researchers become active participants in the group or situation they are studying. Participant observation is very similar to naturalistic observation in that it involves observing people’s behavior in the environment in which it typically occurs. As with naturalistic observation, the data that are collected can include interviews (usually unstructured), notes based on their observations and interactions, documents, photographs, and other artifacts. The only difference between naturalistic observation and participant observation is that researchers engaged in participant observation become active members of the group or situations they are studying. The basic rationale for participant observation is that there may be important information that is only accessible to, or can be interpreted only by, someone who is an active participant in the group or situation. Like naturalistic observation, participant observation can be either disguised or undisguised. In disguised participant observation, the researchers pretend to be members of the social group they are observing and conceal their true identity as researchers.
In a famous example of disguised participant observation, Leon Festinger and his colleagues infiltrated a doomsday cult known as the Seekers, whose members believed that the apocalypse would occur on December 21, 1954. Interested in studying how members of the group would cope psychologically when the prophecy inevitably failed, they carefully recorded the events and reactions of the cult members in the days before and after the supposed end of the world. Unsurprisingly, the cult members did not give up their belief but instead convinced themselves that it was their faith and efforts that saved the world from destruction. Festinger and his colleagues later published a book about this experience, which they used to illustrate the theory of cognitive dissonance (Festinger, Riecken, & Schachter, 1956)[6].
In contrast with undisguised participant observation, the researchers become a part of the group they are studying and they disclose their true identity as researchers to the group under investigation. Once again there are important ethical issues to consider with disguised participant observation. First no informed consent can be obtained and second deception is being used. The researcher is deceiving the participants by intentionally withholding information about their motivations for being a part of the social group they are studying. But sometimes disguised participation is the only way to access a protective group (like a cult). Further, disguised participant observation is less prone to reactivity than undisguised participant observation.
Rosenhan’s study (1973)[7] of the experience of people in a psychiatric ward would be considered disguised participant observation because Rosenhan and his pseudopatients were admitted into psychiatric hospitals on the pretense of being patients so that they could observe the way that psychiatric patients are treated by staff. The staff and other patients were unaware of their true identities as researchers.
Another example of participant observation comes from a study by sociologist Amy Wilkins on a university-based religious organization that emphasized how happy its members were (Wilkins, 2008)[8]. Wilkins spent 12 months attending and participating in the group’s meetings and social events, and she interviewed several group members. In her study, Wilkins identified several ways in which the group “enforced” happiness—for example, by continually talking about happiness, discouraging the expression of negative emotions, and using happiness as a way to distinguish themselves from other groups.
One of the primary benefits of participant observation is that the researchers are in a much better position to understand the viewpoint and experiences of the people they are studying when they are a part of the social group. The primary limitation with this approach is that the mere presence of the observer could affect the behavior of the people being observed. While this is also a concern with naturalistic observation, additional concerns arise when researchers become active members of the social group they are studying because that they may change the social dynamics and/or influence the behavior of the people they are studying. Similarly, if the researcher acts as a participant observer there can be concerns with biases resulting from developing relationships with the participants. Concretely, the researcher may become less objective resulting in more experimenter bias.
Structured Observation
Another observational method is structured observation. Here the investigator makes careful observations of one or more specific behaviors in a particular setting that is more structured than the settings used in naturalistic or participant observation. Often the setting in which the observations are made is not the natural setting. Instead, the researcher may observe people in the laboratory environment. Alternatively, the researcher may observe people in a natural setting (like a classroom setting) that they have structured some way, for instance by introducing some specific task participants are to engage in or by introducing a specific social situation or manipulation.
Structured observation is very similar to naturalistic observation and participant observation in that in all three cases researchers are observing naturally occurring behavior; however, the emphasis in structured observation is on gathering quantitative rather than qualitative data. Researchers using this approach are interested in a limited set of behaviors. This allows them to quantify the behaviors they are observing. In other words, structured observation is less global than naturalistic or participant observation because the researcher engaged in structured observations is interested in a small number of specific behaviors. Therefore, rather than recording everything that happens, the researcher only focuses on very specific behaviors of interest.
Researchers Robert Levine and Ara Norenzayan used structured observation to study differences in the “pace of life” across countries (Levine & Norenzayan, 1999)[9]. One of their measures involved observing pedestrians in a large city to see how long it took them to walk 60 feet. They found that people in some countries walked reliably faster than people in other countries. For example, people in Canada and Sweden covered 60 feet in just under 13 seconds on average, while people in Brazil and Romania took close to 17 seconds. When structured observation takes place in the complex and even chaotic “real world,” the questions of when, where, and under what conditions the observations will be made, and who exactly will be observed are important to consider. Levine and Norenzayan described their sampling process as follows:
“Male and female walking speed over a distance of 60 feet was measured in at least two locations in main downtown areas in each city. Measurements were taken during main business hours on clear summer days. All locations were flat, unobstructed, had broad sidewalks, and were sufficiently uncrowded to allow pedestrians to move at potentially maximum speeds. To control for the effects of socializing, only pedestrians walking alone were used. Children, individuals with obvious physical handicaps, and window-shoppers were not timed. Thirty-five men and 35 women were timed in most cities.” (p. 186).
Precise specification of the sampling process in this way makes data collection manageable for the observers, and it also provides some control over important extraneous variables. For example, by making their observations on clear summer days in all countries, Levine and Norenzayan controlled for effects of the weather on people’s walking speeds. In Levine and Norenzayan’s study, measurement was relatively straightforward. They simply measured out a 60-foot distance along a city sidewalk and then used a stopwatch to time participants as they walked over that distance.
As another example, researchers Robert Kraut and Robert Johnston wanted to study bowlers’ reactions to their shots, both when they were facing the pins and then when they turned toward their companions (Kraut & Johnston, 1979)[10]. But what “reactions” should they observe? Based on previous research and their own pilot testing, Kraut and Johnston created a list of reactions that included “closed smile,” “open smile,” “laugh,” “neutral face,” “look down,” “look away,” and “face cover” (covering one’s face with one’s hands). The observers committed this list to memory and then practiced by coding the reactions of bowlers who had been videotaped. During the actual study, the observers spoke into an audio recorder, describing the reactions they observed. Among the most interesting results of this study was that bowlers rarely smiled while they still faced the pins. They were much more likely to smile after they turned toward their companions, suggesting that smiling is not purely an expression of happiness but also a form of social communication.
In yet another example (this one in a laboratory environment), Dov Cohen and his colleagues had observers rate the emotional reactions of participants who had just been deliberately bumped and insulted by a confederate after they dropped off a completed questionnaire at the end of a hallway. The confederate was posing as someone who worked in the same building and who was frustrated by having to close a file drawer twice in order to permit the participants to walk past them (first to drop off the questionnaire at the end of the hallway and once again on their way back to the room where they believed the study they signed up for was taking place). The two observers were positioned at different ends of the hallway so that they could read the participants' body language and hear anything they might say. Interestingly, the researchers hypothesized that participants from the southern United States, which is one of several places in the world that has a "culture of honor," would react with more aggression than participants from the northern United States, a prediction that was in fact supported by the observational data (Cohen, Nisbett, Bowdle, & Schwarz, 1996)[11].
When the observations require a judgment on the part of the observers—as in the studies by Kraut and Johnston and Cohen and his colleagues—a process referred to as coding is typically required. Coding generally requires clearly defining a set of target behaviors. The observers then categorize participants individually in terms of which behavior they have engaged in and the number of times they engaged in each behavior. The observers might even record the duration of each behavior. The target behaviors must be defined in such a way that guides different observers to code them in the same way. This difficulty with coding illustrates the issue of interrater reliability, as mentioned in Chapter 4. Researchers are expected to demonstrate the interrater reliability of their coding procedure by having multiple raters code the same behaviors independently and then showing that the different observers are in close agreement. Kraut and Johnston, for example, video recorded a subset of their participants’ reactions and had two observers independently code them. The two observers showed that they agreed on the reactions that were exhibited 97% of the time, indicating good interrater reliability.
One of the primary benefits of structured observation is that it is far more efficient than naturalistic and participant observation. Since the researchers are focused on specific behaviors this reduces time and expense. Also, often times the environment is structured to encourage the behaviors of interest which again means that researchers do not have to invest as much time in waiting for the behaviors of interest to naturally occur. Finally, researchers using this approach can clearly exert greater control over the environment. However, when researchers exert more control over the environment it may make the environment less natural which decreases external validity. It is less clear for instance whether structured observations made in a laboratory environment will generalize to a real world environment. Furthermore, since researchers engaged in structured observation are often not disguised there may be more concerns with reactivity.
Case Studies
A case study is an in-depth examination of an individual. Sometimes case studies are also completed on social units (e.g., a cult) and events (e.g., a natural disaster). Most commonly in psychology, however, case studies provide a detailed description and analysis of an individual. Often the individual has a rare or unusual condition or disorder or has damage to a specific region of the brain.
Like many observational research methods, case studies tend to be more qualitative in nature. Case study methods involve an in-depth, and often a longitudinal examination of an individual. Depending on the focus of the case study, individuals may or may not be observed in their natural setting. If the natural setting is not what is of interest, then the individual may be brought into a therapist’s office or a researcher’s lab for study. Also, the bulk of the case study report will focus on in-depth descriptions of the person rather than on statistical analyses. With that said some quantitative data may also be included in the write-up of a case study. For instance, an individual's depression score may be compared to normative scores or their score before and after treatment may be compared. As with other qualitative methods, a variety of different methods and tools can be used to collect information on the case. For instance, interviews, naturalistic observation, structured observation, psychological testing (e.g., IQ test), and/or physiological measurements (e.g., brain scans) may be used to collect information on the individual.
HM is one of the most notorious case studies in psychology. HM suffered from intractable and very severe epilepsy. A surgeon localized HM’s epilepsy to his medial temporal lobe and in 1953 he removed large sections of his hippocampus in an attempt to stop the seizures. The treatment was a success, in that it resolved his epilepsy and his IQ and personality were unaffected. However, the doctors soon realized that HM exhibited a strange form of amnesia, called anterograde amnesia. HM was able to carry out a conversation and he could remember short strings of letters, digits, and words. Basically, his short term memory was preserved. However, HM could not commit new events to memory. He lost the ability to transfer information from his short-term memory to his long term memory, something memory researchers call consolidation. So while he could carry on a conversation with someone, he would completely forget the conversation after it ended. This was an extremely important case study for memory researchers because it suggested that there’s a dissociation between short-term memory and long-term memory, it suggested that these were two different abilities sub-served by different areas of the brain. It also suggested that the temporal lobes are particularly important for consolidating new information (i.e., for transferring information from short-term memory to long-term memory).

The history of psychology is filled with influential cases studies, such as Sigmund Freud’s description of “Anna O.” (see Note 6.1 "The Case of “Anna O.”") and John Watson and Rosalie Rayner’s description of Little Albert (Watson & Rayner, 1920)[12], who allegedly learned to fear a white rat—along with other furry objects—when the researchers repeatedly made a loud noise every time the rat approached him.
The Case of “Anna O.”
Sigmund Freud used the case of a young woman he called “Anna O.” to illustrate many principles of his theory of psychoanalysis (Freud, 1961)[13]. (Her real name was Bertha Pappenheim, and she was an early feminist who went on to make important contributions to the field of social work.) Anna had come to Freud’s colleague Josef Breuer around 1880 with a variety of odd physical and psychological symptoms. One of them was that for several weeks she was unable to drink any fluids. According to Freud,
She would take up the glass of water that she longed for, but as soon as it touched her lips she would push it away like someone suffering from hydrophobia.…She lived only on fruit, such as melons, etc., so as to lessen her tormenting thirst. (p. 9)
But according to Freud, a breakthrough came one day while Anna was under hypnosis.
[S]he grumbled about her English “lady-companion,” whom she did not care for, and went on to describe, with every sign of disgust, how she had once gone into this lady’s room and how her little dog—horrid creature!—had drunk out of a glass there. The patient had said nothing, as she had wanted to be polite. After giving further energetic expression to the anger she had held back, she asked for something to drink, drank a large quantity of water without any difficulty, and awoke from her hypnosis with the glass at her lips; and thereupon the disturbance vanished, never to return. (p.9)
Freud’s interpretation was that Anna had repressed the memory of this incident along with the emotion that it triggered and that this was what had caused her inability to drink. Furthermore, he believed that her recollection of the incident, along with her expression of the emotion she had repressed, caused the symptom to go away.
As an illustration of Freud’s theory, the case study of Anna O. is quite effective. As evidence for the theory, however, it is essentially worthless. The description provides no way of knowing whether Anna had really repressed the memory of the dog drinking from the glass, whether this repression had caused her inability to drink, or whether recalling this “trauma” relieved the symptom. It is also unclear from this case study how typical or atypical Anna’s experience was.

Case studies are useful because they provide a level of detailed analysis not found in many other research methods and greater insights may be gained from this more detailed analysis. As a result of the case study, the researcher may gain a sharpened understanding of what might become important to look at more extensively in future more controlled research. Case studies are also often the only way to study rare conditions because it may be impossible to find a large enough sample of individuals with the condition to use quantitative methods. Although at first glance a case study of a rare individual might seem to tell us little about ourselves, they often do provide insights into normal behavior. The case of HM provided important insights into the role of the hippocampus in memory consolidation.
However, it is important to note that while case studies can provide insights into certain areas and variables to study, and can be useful in helping develop theories, they should never be used as evidence for theories. In other words, case studies can be used as inspiration to formulate theories and hypotheses, but those hypotheses and theories then need to be formally tested using more rigorous quantitative methods. The reason case studies shouldn’t be used to provide support for theories is that they suffer from problems with both internal and external validity. Case studies lack the proper controls that true experiments contain. As such, they suffer from problems with internal validity, so they cannot be used to determine causation. For instance, during HM’s surgery, the surgeon may have accidentally lesioned another area of HM's brain (a possibility suggested by the dissection of HM's brain following his death) and that lesion may have contributed to his inability to consolidate new information. The fact is, with case studies we cannot rule out these sorts of alternative explanations. So, as with all observational methods, case studies do not permit determination of causation. In addition, because case studies are often of a single individual, and typically an abnormal individual, researchers cannot generalize their conclusions to other individuals. Recall that with most research designs there is a trade-off between internal and external validity. With case studies, however, there are problems with both internal validity and external validity. So there are limits both to the ability to determine causation and to generalize the results. A final limitation of case studies is that ample opportunity exists for the theoretical biases of the researcher to color or bias the case description. Indeed, there have been accusations that the woman who studied HM destroyed a lot of her data that were not published and she has been called into question for destroying contradictory data that didn’t support her theory about how memories are consolidated. There is a fascinating New York Times article that describes some of the controversies that ensued after HM's death and analysis of his brain that can be found at: https://www.nytimes.com/2016/08/07/magazine/the-brain-that-couldnt-remember.html?_r=0
Archival Research
Another approach that is often considered observational research involves analyzing archival data that have already been collected for some other purpose. An example is a study by Brett Pelham and his colleagues on “implicit egotism”—the tendency for people to prefer people, places, and things that are similar to themselves (Pelham, Carvallo, & Jones, 2005)[14]. In one study, they examined Social Security records to show that women with the names Virginia, Georgia, Louise, and Florence were especially likely to have moved to the states of Virginia, Georgia, Louisiana, and Florida, respectively.
As with naturalistic observation, measurement can be more or less straightforward when working with archival data. For example, counting the number of people named Virginia who live in various states based on Social Security records is relatively straightforward. But consider a study by Christopher Peterson and his colleagues on the relationship between optimism and health using data that had been collected many years before for a study on adult development (Peterson, Seligman, & Vaillant, 1988)[15]. In the 1940s, healthy male college students had completed an open-ended questionnaire about difficult wartime experiences. In the late 1980s, Peterson and his colleagues reviewed the men’s questionnaire responses to obtain a measure of explanatory style—their habitual ways of explaining bad events that happen to them. More pessimistic people tend to blame themselves and expect long-term negative consequences that affect many aspects of their lives, while more optimistic people tend to blame outside forces and expect limited negative consequences. To obtain a measure of explanatory style for each participant, the researchers used a procedure in which all negative events mentioned in the questionnaire responses, and any causal explanations for them were identified and written on index cards. These were given to a separate group of raters who rated each explanation in terms of three separate dimensions of optimism-pessimism. These ratings were then averaged to produce an explanatory style score for each participant. The researchers then assessed the statistical relationship between the men’s explanatory style as undergraduate students and archival measures of their health at approximately 60 years of age. The primary result was that the more optimistic the men were as undergraduate students, the healthier they were as older men. Pearson’s r was +.25.
This method is an example of content analysis—a family of systematic approaches to measurement using complex archival data. Just as structured observation requires specifying the behaviors of interest and then noting them as they occur, content analysis requires specifying keywords, phrases, or ideas and then finding all occurrences of them in the data. These occurrences can then be counted, timed (e.g., the amount of time devoted to entertainment topics on the nightly news show), or analyzed in a variety of other ways.
Learning Objectives
- Explain some reasons that researchers use complex correlational designs.
- Create and interpret a correlation matrix.
- Describe how researchers can use partial correlation and multiple regression to statistically control for third variables.
As we have already seen, researchers conduct correlational studies rather than experiments when they are interested in noncausal relationships or when they are interested in causal relationships but the independent variable cannot be manipulated for practical or ethical reasons. In this section, we look at some approaches to complex correlational research that involve measuring several variables and assessing the relationships among them.
Assessing Relationships Among Multiple Variables
Most complex correlational research involves measuring several variables—either binary or continuous—and then assessing the statistical relationships among them. For example, researchers Nathan Radcliffe and William Klein studied a sample of middle-aged adults to see how their level of optimism (measured by using a short questionnaire called the Life Orientation Test) relates to several other variables related to having a heart attack (Radcliffe & Klein, 2002)[16]. These included their health, their knowledge of heart attack risk factors, and their beliefs about their own risk of having a heart attack. They found that more optimistic participants were healthier (e.g., they exercised more and had lower blood pressure), knew about heart attack risk factors, and correctly believed their own risk to be lower than that of their peers.
In another example, Ernest Jouriles and his colleagues measured adolescents' experiences of physical and psychological relationship aggression and their psychological distress. Because measures of physical aggression (such as the Conflict in Adolescent Dating Relationships Inventory and the Relationship Violence Interview) often tend to result in highly skewed distributions, the researchers transformed their measures of physical aggression into a dichotomous (i.e., binary) measure (0 = did not occur, 1 = did occur). They did the same with their measures of psychological aggression and then measured the correlations among these variables, finding that adolescents who experienced physical aggression were moderately likely to also have experienced psychological aggression and that experiencing psychological aggression was related to symptoms of psychological distress. (Jouriles, Garrido, Rosenfield, & McDonald, 2009)[17]
This approach is often used to assess the validity of new psychological measures. For example, when John Cacioppo and Richard Petty created their Need for Cognition Scale—a measure of the extent to which people like to think and value thinking—they used it to measure the need for cognition for a large sample of college students, along with three other variables: intelligence, socially desirable responding (the tendency to give what one thinks is the “appropriate” response), and dogmatism (Caccioppo & Petty, 1982)[18]. The results of this study are summarized in Table 6.1, which is a correlation matrix showing the correlation (Pearson’s r) between every possible pair of variables in the study. For example, the correlation between the need for cognition and intelligence was +.39, the correlation between intelligence and socially desirable responding was +.02, and so on. (Only half the matrix is filled in because the other half would contain exactly the same information. Also, because the correlation between a variable and itself is always +1.00, these values are replaced with dashes throughout the matrix.) In this case, the overall pattern of correlations was consistent with the researchers’ ideas about how scores on the need for cognition should be related to these other constructs.
Table 6.1 Correlation Matrix Showing Correlations Among the Need for Cognition and Three Other Variables Based on Research by Cacioppo and Petty (1982)
| Need for cognition | Intelligence | Social desirability | Dogmatism | |
| Need for cognition | — | |||
| Intelligence | +.39 | — | ||
| Social desirability | +.08 | +.02 | — | |
| Dogmatism | −.27 | −.23 | +.03 | — |
Factor Analysis
When researchers study relationships among a large number of conceptually similar variables, they often use a complex statistical technique called factor analysis. In essence, factor analysis organizes the variables into a smaller number of clusters, such that they are strongly correlated within each cluster but weakly correlated between clusters. Each cluster is then interpreted as multiple measures of the same underlying construct. These underlying constructs are also called “factors.” For example, when people perform a wide variety of mental tasks, factor analysis typically organizes them into two main factors—one that researchers interpret as mathematical intelligence (arithmetic, quantitative estimation, spatial reasoning, and so on) and another that they interpret as verbal intelligence (grammar, reading comprehension, vocabulary, and so on). The Big Five personality factors have been identified through factor analyses of people’s scores on a large number of more specific traits. For example, measures of warmth, gregariousness, activity level, and positive emotions tend to be highly correlated with each other and are interpreted as representing the construct of extraversion. As a final example, researchers Peter Rentfrow and Samuel Gosling asked more than 1,700 university students to rate how much they liked 14 different popular genres of music (Rentfrow & Gosling, 2008)[19]. They then submitted these 14 variables to a factor analysis, which identified four distinct factors. The researchers called them Reflective and Complex (blues, jazz, classical, and folk), Intense and Rebellious (rock, alternative, and heavy metal), Upbeat and Conventional (country, soundtrack, religious, pop), and Energetic and Rhythmic (rap/hip-hop, soul/funk, and electronica); see Table 6.2.
Table 6.2 Factor Loadings of the 14 Music Genres on Four Varimax-Rotated Principal Components. Based on Research by Rentfrow and Gosling (2003)
| Music-preference dimension | ||||
| Genre | Reflective and Complex | Intense and Rebellious | Upbeat and Conventional | Energetic and Rhythmic |
| Blues | .85 | .01 | -.09 | .12 |
| Jazz | .83 | .04 | .07 | .15 |
| Classical | .66 | .14 | .02 | -.13 |
| Folk | .64 | .09 | .15 | -.16 |
| Rock | .17 | .85 | -.04 | -.07 |
| Alternative | .02 | .80 | .13 | .04 |
| Heavy metal | .07 | .75 | -.11 | .04 |
| Country | -.06 | .05 | .72 | -.03 |
| Sound tracks | .01 | .04 | .70 | .17 |
| Religious | .23 | -.21 | .64 | -.01 |
| Pop | -.20 | .06 | .59 | .45 |
| Rap/hip-hop | -.19 | -.12 | .17 | .79 |
| Soul/funk | .39 | -.11 | .11 | .69 |
| Electronica/dance | -.02 | .15 | -.01 | .60 |
| Note. N = 1,704. All factor loadings .40 or larger are in italics; the highest factor loadings for each dimension are listed in boldface type. |
||||
Two additional points about factor analysis are worth making here. One is that factors are not categories. Factor analysis does not tell us that people are either extraverted or conscientious or that they like either “reflective and complex” music or “intense and rebellious” music. Instead, factors are constructs that operate independently of each other. So people who are high in extraversion might be high or low in conscientiousness, and people who like reflective and complex music might or might not also like intense and rebellious music. The second point is that factor analysis reveals only the underlying structure of the variables. It is up to researchers to interpret and label the factors and to explain the origin of that particular factor structure. For example, one reason that extraversion and the other Big Five operate as separate factors is that they appear to be controlled by different genes (Plomin, DeFries, McClean, & McGuffin, 2008)[20].
Exploring Causal Relationships
Another important use of complex correlational research is to explore possible causal relationships among variables. This might seem surprising given the oft-quoted saying that "correlation does not imply causation.” It is true that correlational research cannot unambiguously establish that one variable causes another. Complex correlational research, however, can often be used to rule out other plausible interpretations. The primary way of doing this is through the statistical control of potential third variables. Instead of controlling these variables through random assignment or by holding them constant as in an experiment, the researcher instead measures them and includes them in the statistical analysis called partial correlation. Using this technique, researchers can examine the relationship between two variables, while statistically controlling for one or more potential third variables.
For example, assume a researcher was interested in the relationship between watching violent television shows and aggressive behavior but she was concerned that socioeconomic status (SES) might represent a third variable that is driving this relationship. In this case, she could conduct a study in which she measures the amount of violent television that participants watch in their everyday life, the number of acts of aggression that they have engaged in, and their SES. She could first examine the correlation between violent television viewing and aggression. Let's say she found a correlation of +.35, which would be considered a moderate sized positive correlation. Next, she could use partial correlation to reexamine this relationship after statistically controlling for SES. This technique would allow her to examine the relationship between the part of violent television viewing that is independent of SES and the part of aggressive behavior that is independent of SES. If she found that the partial correlation between violent television viewing and aggression while controlling for SES was +.34, that would suggest that the relationship between violent television viewing and aggression is largely independent of SES (i.e., SES is not a third variable driving this relationship). On the other hand, if she found that after statistically controlling for SES the correlation between violent television viewing and aggression dropped to +.03, then that would suggest that SES is indeed a third variable that is driving the relationship. If, however, she found that statistically controlling for SES reduced the magnitude of the correlation from +.35 to +.20, then this would suggest that SES accounts for some, but not all, of the relationship between television violence and aggression. It is important to note that while partial correlation provides an important tool for researchers to statistically control for third variables, researchers using this technique are still limited in their ability to arrive at causal conclusions because this technique does not take care of the directionality problem and there may be other third variables driving the relationship that the researcher did not consider and statistically control.
Regression
Once a relationship between two variables has been established, researchers can use that information to make predictions about the value of one variable given the value of another variable. For, instance, once we have established that there is a correlation between IQ and GPA we can use people's IQ scores to predict their GPA. Thus, while correlation coefficients can be used to describe the strength and direction of relationships between variables, regression is a statistical technique that allows researchers to predict one variable given another. Regression can also be used to describe more complex relationships between more than two variables. Typically the variable that is used to make the prediction is referred to as the predictor variable and the variable that is being predicted is called the outcome variable or criterion variable. This regression equation has the following general form:
Y = b1X1
Y in this formula represents the person's predicted score on the outcome variable, b1 represents the slope of the line depicting the relationship between two variables (or the regression weight), and X1 represents the person's score on the predictor variable. You can see that to predict a person's score on the outcome variable (Y), one simply needs to multiply their score on the predictor variable (X) by the regression weight (b1 )
While simple regression involves using one variable to predict another, multiple regression involves measuring several variables (X1, X2, X3,…Xi), and using them to predict some outcome variable (Y). Multiple regression can also be used to simply describe the relationship between a single outcome variable (Y) and a set of predictor variables (X1, X2, X3,…Xi). The result of a multiple regression analysis is an equation that expresses the outcome variable as an additive combination of the predictor variables. This regression equation has the following general form:
Y = b1X1+ b2X2+ b3X3+ … + biXi
The regression weights (b1, b2, and so on) indicate how large a contribution a predictor variable makes, on average, to the prediction of the outcome variable. Specifically, they indicate how much the outcome variable changes for each one-unit change in the predictor variable.
The advantage of multiple regression is that it can show whether a predictor variable makes a contribution to an outcome variable over and above the contributions made by other predictor variables (i.e., it can be used to show whether a predictor variable is related to an outcome variable after statistically controlling for other predictor variables). As a hypothetical example, imagine that a researcher wants to know how income and health relate to happiness. This is tricky because income and health are themselves related to each other. Thus if people with greater incomes tend to be happier, then perhaps this is only because they tend to be healthier. Likewise, if people who are healthier tend to be happier, perhaps this is only because they tend to make more money. But a multiple regression analysis including both income and health as predictor variables would show whether each one makes a contribution to the prediction of happiness when the other is taken into account (when it is statistically controlled). In other words, multiple regression would allow the researcher to examine whether that part of income that is unrelated to health predicts or relates to happiness as well as whether that part of health that is unrelated to income predicts or relates to happiness. Research like this, by the way, has shown both income and health make extremely small contributions to happiness except in the case of severe poverty or illness (Diener, 2000[21]).
The examples discussed in this section only scratch the surface of how researchers use complex correlational research to explore possible causal relationships among variables. It is important to keep in mind, however, that purely correlational approaches cannot unambiguously establish that one variable causes another. The best they can do is show patterns of relationships that are consistent with some causal interpretations and inconsistent with others.


