Gravitational Lensing
Introduction
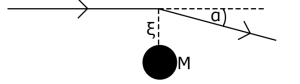
Though gravitational lensing is usually associated, and correctly described by, Einstein’s theory of general relativity, the phenomena is predicted by classic Newtonian physics. The amount of deflection is determined by integrating along the path of the photon moving by a point mass ![]() , as in Figure 1. The Newtonian deflection angle for the photon was found to be
, as in Figure 1. The Newtonian deflection angle for the photon was found to be
(1) ![]()
Figure 1: A simple representation of gravitational deflection.
where ![]() is the gravitational constant,
is the gravitational constant, ![]() is the speed of light, and
is the speed of light, and ![]() is the ’impact parameter’ or distance of closest approach. In general relativity, 3D space is distorted by the gravitational field of massive bodies. A good analogy is a plastic film stretched across a hoop. Masses distort 3D space the way pushing down on the film with your finger distorts the film. In fact, this same analogy applies to electrostatics, and is the hallmark of a field that can be described by the Poisson equation (if this is the first time you are hearing about Poisson’s equation, please google/wiki it. It’s super powerful, and is a generalization of Laplace’s equation, which comes up a lot, too). Due to this distortion of space, one must account for gravitational effects on the spatial AND temporal components of the photons path, resulting in twice the deflection angle:
is the ’impact parameter’ or distance of closest approach. In general relativity, 3D space is distorted by the gravitational field of massive bodies. A good analogy is a plastic film stretched across a hoop. Masses distort 3D space the way pushing down on the film with your finger distorts the film. In fact, this same analogy applies to electrostatics, and is the hallmark of a field that can be described by the Poisson equation (if this is the first time you are hearing about Poisson’s equation, please google/wiki it. It’s super powerful, and is a generalization of Laplace’s equation, which comes up a lot, too). Due to this distortion of space, one must account for gravitational effects on the spatial AND temporal components of the photons path, resulting in twice the deflection angle:
(2) ![]()
The first experimental verification of gravitational lensing came in 1919 during a total solar eclipse. Astronomers observed stars as their light passed by the Sun, and measured the difference between their known position and apparent positions. The deflection was measured to be ![]() arcseconds. Compare this measurement with the result of Equation (2) when using the mass and radius of the Sun.
arcseconds. Compare this measurement with the result of Equation (2) when using the mass and radius of the Sun.
Gravitational lensing has proved useful in a few specific astronomical scenarios. Since the deflection associated with gravitational lensing depends only on the mass of the lensing object, and not the type of mass, observing the deflection of light around an astronomical body can be used to identify objects too faint to see. Even when an object can be seen, the deflection of light can give insights into how much dark matter the object, like a galaxy or cluster of galaxies, may contain. In a few rare cases, this deflection of light has been associated with exoplanets [6].
It’s not obvious now, but the gravitational deflection of light can lead to magnification of the source object, which is why we call it gravitational lensing. Gravitational lensing has been used to image highredshift galaxies that would have been too faint to see otherwise [8].
2.1 Gravitational Lensing Formalism
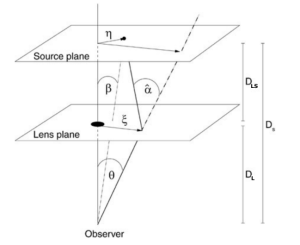
Consider the schematic diagram of a lensing system shown in Figure 2. We define three planes: The source plane, the lens plane, and the observer plane. The line between the observer and the lens defines the axis. Consider a source a distance ![]() and true angle
and true angle ![]() from the center axis, and distance
from the center axis, and distance ![]() from the observer. A ray of light from the source can pass by the lens at distance
from the observer. A ray of light from the source can pass by the lens at distance ![]() , and appear to the observer as if it originated from a source at an apparent angle
, and appear to the observer as if it originated from a source at an apparent angle ![]() . One can derive a lens equation for this system such that
. One can derive a lens equation for this system such that
(3) ![]()
We can define a reduced deflection angle ![]() , then we attain a simple lens equation:
, then we attain a simple lens equation:
(4) ![]()
Note that it is possible to have multiple solutions to this lens equation, resulting in multiple images at the observer. From Equation (2), we know the deflection angle in terms of the impact parameter ![]() , which, presuming the angles involved are small,
, which, presuming the angles involved are small, ![]() . Using the deflection angle for a point mass from Equation (2), the lens equation becomes
. Using the deflection angle for a point mass from Equation (2), the lens equation becomes
(5) ![]()
where
(6) 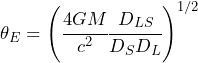
is the so-called Einstein angle (sometimes referred to as the Einstein radius) that occurs when ![]() and the source, lens, and observer lie on the same line.
and the source, lens, and observer lie on the same line.
2.2 Strong Gravitational Lensing
Figure 3: Examples of strong lens systems that produce arcs and Einstein rings. Figure from Reference [3]
Strong gravitational lensing is usually an obvious phenomenon when one sees it. Arcs and rings, like those in Figure 3 are very characteristic of gravitational lensing. A phenomenon that is caused by gravitational lensing, but is less obvious, is the production of multiple images. The first example discovered by astronomers was a twin quasar system 0957+567 A,B [9]. The two quasars have very similar red shift and spectrum, which lead researchers to believe that they are actually the same quasar with two images produced by gravitational lensing caused by galaxy YGKOW G1 and its cluster.
Systems that exhibit strong gravitational lensing resulting in Einstein rings are probably the easiest of the scenarios to analyze. Astronomers measure the Einstein radius, usually in units of arcseconds, then measure or model the distances between the lens and source objects to determine the mass of the lensing object.