Electron Diffraction
Procedure
WARNING!!! You will be using diode lasers. A general rule when using lasers is to AVOID PUTTING YOUR FACE IN THE PLANE OF THE LASER. You have no reason to put your face anywhere near the laser, so please don’t.
4.1 Diffraction of Light
You’ll start by studying the diffraction of light, which is nice since then we actually touch the experiment components and don’t have to work in a vacuum.
- Start by turning on the white light from the headlamp and holding it right to the input of the diffraction grating. Notice how the light is separated into its component wavelengths. Which wavelengths are diffracted to the largest angles?
- Start with the red diode laser.
- Mount the diode laser in the little claw. You will have to loosen and tighten the claw when installing the diode laser, which can lead to unwanted misalignment between the diode laser and face of the diffraction grating (we want a perfectly perpendicular trajectory of the diode laser).
- The lasers require the user to hold down the power button if they want laser output. This is a safety measure to make sure the laser is not accidentally left on when the user goes to change the apparatus or take a position measurement.
- Set the alignment tool on the optical rail close to the laser. Slide the alignment tool away from the laser and adjust the laser/claw so that the laser is striking the alignment tool at approximately the same position as you slide the tool along the optical rail.
- Make sure the angle of the diffraction-grating holder is set to 90
 so that the gratings are vertically oriented. What will the output look like when the gratings are vertical? Note that you may need to make a slight adjustment away from 90
so that the gratings are vertically oriented. What will the output look like when the gratings are vertical? Note that you may need to make a slight adjustment away from 90 for the output to be perfectly horizontal.
for the output to be perfectly horizontal. - Move the alignment tool to the perpendicular rail on the other side of the diffraction grating. We’ll now use it to mark the position of the diffracted laser.
- With the laser on, hopefully you can see at least the
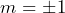 and
and 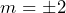 outputs.
outputs. - Use the ruler on the optical rail to determine the positions of the diffracted beams. Use that measured position, the distance between the diffraction grating and perpendicular optical rail, and trigonometry to determine the diffraction angle. Try to estimate the uncertainties in your position measurements. You should have measurements for AT LEAST the
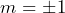 and
and 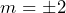 outputs, but maybe more (which would be great!).
outputs, but maybe more (which would be great!). - Swap lasers, check the alignment, and repeat your measurements. You should have three sets of data: one for each colour.
- Rotate the diffraction grating by 90
 . Take a single measurement with a ruler (you don’t have to be very precise). Does Equation (1) still hold? What would the diffraction pattern look like if the grating were quickly rotating? Or if you were looking at the result of many, many gratings at random angles?
. Take a single measurement with a ruler (you don’t have to be very precise). Does Equation (1) still hold? What would the diffraction pattern look like if the grating were quickly rotating? Or if you were looking at the result of many, many gratings at random angles? - Considering the relationship between the frequency and energy of a photon, what does this experiment imply about the diffraction of matter, such as electrons, as a function of energy?
4.2 Diffraction of Matter
Make sure you are confident using a Vernier caliper to measure distances precisely. Talk to your TA and/or check out this helpful video.
- Turn on the power supply. The AC voltage (that you don’t control) will heat up the electron source. Turn the high voltage (that you DO control) to about 2 kV. You should see a bright green dot on the face of the fluorescent detector. This is the un-diffracted (
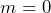 ) electron beam.
) electron beam. - Start at highest HV possible – about 5 kV. How many rings do you see? Measure the diameter of each ring with the Vernier calipers.
- Decrease the high voltage in steps of about 500 V. Measure the diameter of the rings at each step (you may not see two rings as you get to lower high-voltage settings).
- How does the ring diameter change as a function of applied voltage? Is that in accordance with the DeBroglie equation?
4.3 Before You Leave
Take a moment to talk with Dr. FitzGreen about your data from the two different diffraction experiments. There are important comparisons and conclusions to make.
