2.1 Diffraction

Diffraction is a pretty general concept: When a wave hits an obstacle, it’s energy spreads out and the wave can enter space that the observer may not expect based on the geometry of the scenario. You have probably noticed by now that you can shout and someone around the corner can hear you. If waves didn’t diffract, then that wouldn’t happen. And you are probably quite familiar with the double-slit experiment that demonstrated the diffraction and interference of light, thereby proving that it is a wave. Hopefully you’ve seen something like the pattern in Figure 1 in your physics education already.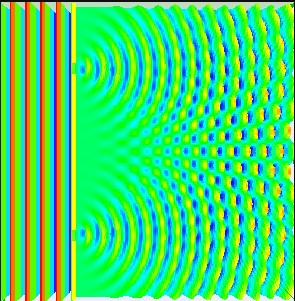

Figure 1: The interference pattern that arises from an electromagnetic wave hitting a barrier with two thin slits.

    In your experiment today, you will explore two regimes of diffraction: optical diffraction with a diode laser and diffraction grating, and the diffraction of a matter wave (electrons) by a crystal lattice of carbon.

These experiments really emphasize the particle-wave duality of matter, which is a central pillar of quantum mechanics.

2.2 Optical Diffraction

Optical diffraction can be predicted by the Huygens-Fresnel principle, which states that every point of a plane wave can be approximated by a little tiny spherical wave. So when a plane wave, like the electromagnetic wave (i.e. light) from the laser diode, hits a barrier with a slit, then the tiny spherical waves propagate through and result in a curved wavefront, like the ones in Figure 1. The thinner the slit, the more curved the outgoing wavefront will be. And things get really interesting when there are MANY small slits for the light to diffract through. The interference pattern from the double-slit experiment is repeated many times over (when you get to the ‘Experimental Apparatus’ section, you will see exactly how many we are talking about here). As the number of slits increases, the diffraction pattern from Figure 1 reduces to a set of discrete points where all of the tiny spherical waves constructively interfere. This diffraction pattern is the result of the slight differences in path length between the diffracted waves, as shown in Figure 2.

Figure 2: (a) Constructive and destructive(ish) interference as waves pass through a barrier with a series of slits. (b) the diffraction pattern from a beam of monochromatic light passing through a transmissive diffraction grating.

The interference pattern is quantified by

(1)  

where is the distance between slits in the diffraction grating,  is the angle that the diffracted light undergoes,  is an integer indicating the order of the output beam (i.e. first order, second order, etc..), and  is the wavelength of the light.

2.3 Diffraction of Matter

In 1924, Louis De Broglie postulated (for his PhD thesis, no less) that even matter has a wavelength, given by:

(2)  

where  is Planck’s constant and is the momentum of the mass (do not confuse that  with the  indicating the order of the diffraction output). Macroscopic masses have incredibly small wavelengths: a 75 kg human walking at about 1 m/s would have a wavelength of about 10⁻³⁷ m. For reference, a proton has a diameter of about 10⁻¹⁵ m; so don’t worry about diffracting if you bump into a wall or anything. But consider an electron moving at about 1% the speed of light. The resulting wavelength is about 10⁻¹⁰ m – comparable to the size of atomic lattice structures in crystals! Therefore, we can use an electron beam to study crystal lattices as long as we know the momentum of the electron beam and the angle of the diffracted electrons.