"

5 Part 1: Simple Pendulum

SETUP

First, we will examine a simple pendulum. A small ball is attached to a string and hung from a pivot. You will release the ball from various angles and lengths of the string to measure the period of the swing, as described in each part below.

PART A: PRELIMINARY STUDY

The first part of the lab will help us get more acquainted with the types of uncertainties we are measuring in this lab and to determine the best way to measure the period of the simple pendulum with a stopwatch.

PROCEDURE

1.   Set the length of the simple pendulum to be 10cm and position the ball bearing to have a small amplitude (small angle, < 15º) from the center. Make sure that the amplitude (point at which you release the ball bearing at) is relatively close to the center, i.e. your release angle should be less than 15º.

a.   Note: the release point does not need to be exactly the same for each measurement in this part, so long as it starts relatively close to the center.

2.   Use the stopwatch to determine the period of the simple pendulum by measuring the time for various numbers of swings. One partner will release the pendulum while the other partner will time the period with the stopwatch and record the data. Then, switch. Note: This is the only part of the lab where both partners must take the same measurements.

a.   Think carefully about what the uncertainty in time should be for a human interacting with the stopwatch.

3.   Each lab partner will measure the period for 1, 5, and 10 swings.  Record the time for the various number of swings in the Results section for each lab partner.

4.   While conducting this experiment, consider what would make the most sense as the uncertainty in time. Should we be using the smallest increment on the stopwatch, or do we need to consider the observer’s reaction time? Discuss with your partner, and decide on your uncertainty value for your stopwatch measurements. (Please refer to the “Laboratory general guide lines” to determine a total uncertainty.) Record the uncertainty value of your measurements after the plus/minus sign at the top of the Part A: Results table in your report.

a.   IMPORTANT!!! This will be the uncertainty that we use for the remainder of the simple pendulum experiment.

CHECKPOINT:

(Ask the TA to check your uncertainty in time.)

5.   Calculate the period of one swing using the measurements in each set and record them in your table in the Results section. Also record the uncertainty for each period.

Answer the following questions in the ‘Discussion’ section of your report:

 

Question 1.

How does having more swings affect the measurement of the time? Does it affect your calculated periods and associated uncertainties? Explain.

 

Question 2.

Can you eliminate your reaction time between the moment you see the pendulum and the moment you press the stopwatch? Does it help if two different people do the timing?

 

Question 3.

Does the non-rigidity of the pendulum support affect the measurement? Explain why or why not.

 

 

PART B: VARIATION WITH AMPLITUDE

In this part we check the variation of period with the amplitude of swing. The goal of this part is to show at which amplitudes Equation (2) holds.  (Note: we will not concern ourselves with the uncertainty in amplitude.)

PROCEDURE

1.   Select a convenient pendulum length for which you will measure 10 swings.

2.   Measure the period for a small (~5°) and record your results in the report. Repeat the measurements for 5 more angles. The largest angle that can be used is about 60°.

3.   Open Excel and copy your data in the worksheet titled ‘PART B’. The excel worksheet will build a plot of period (T) versus amplitude as you fill in the data.

a.   The horizontal scale on which you plot the amplitude should run from 0 on the left to 60° on the right, with a scale that covers the entire domain of values for amplitude.

b.   As you fill in the data, the vertical scale on the Excel graph should change such that you will see the uncertainty ranges and the variation of the period clearly.

4.   Before copying your plot into the Results section of your report, make sure that your x and y-axes are scaled such that your data fits well in the plot area. Also make sure to label your graph.

a.   To change the scale of your axes, right click on the axis in question, click ‘Format Axis,’ and a pop-up window will allow you to change the axis minimum and maximum.

b.   Note: For the first lab, we will provide you with appropriate axis labels and plot titles. In future labs, it is up to you to ensure that all of your graphs are properly titled, and have accurate axis labels.

Answer the following questions:

Question 4. 

Is period independent of amplitude for the simple pendulum?  Refer to your Excel plot from worksheet Part B in your answer. If you had timed only a single swing for each amplitude, would it have affected your answer to this question? Explain why or why not.

Hint: Does Equation (1) hold true for all angles, or only for a given range?

 

 

Question 5.

Recall that to derive Equation (1), we assumed a small amplitude. Based on your plot generated in Excel for PART B, how large can your amplitude be before this small-amplitude approximation begins to breakdown? Explain, using your graph to justify your answer.
Hint: You can see that if your measurements were more precise (smaller error bars) the maximum amplitude value would be both smaller and more clearly defined.

 

PART C: VARIATION WITH LENGTH

In the final part of the simple pendulum experiment, we will experimentally determine the gravitational constant g = 9.81 m/s^2. We will do this with two methods. First, we will measure the period for a simple pendulum at a fixed amplitude with various lengths, and then calculate the value of g from Equation (2). Then, we will find the line of best fit from a plot of period square (T^2) versus length (l), and use the slope of the line to determine a value for g. Before we go to the procedure, consider the following question.

Question 6.

To what point on the mass do you measure l? (The theory assumes a point mass, but does it make any difference which point is used?)

 

PROCEDURE

1.   Select an easily measured amplitude for which you have shown the simple pendulum theory to be valid (i.e. an angle for which the small-angle approximation holds). Position the ball at a constant angle from the centre, and record your chosen angle at the top of your chart in the Results section of Part C.

a.   Note: keep your angle constant throughout the remainder of this part.

2.   Using this amplitude throughout, determine the periods for 5 different lengths with 10 swings, spaced uniformly over a large range and record them in your table in the Results section. We suggest that you start with 10cm and don’t go past 80cm in length. Record your results in the table under Part C (don’t forget to include the uncertainty in the period at the top).

3.   From your measurements, calculate the values of T^2 and g only for the first set of measurements. Also, determine the correct formula for the error in T^2 (\delta(T^2)) and for the error in g (\delta(g)) using Equation (2), and propagating the error accordingly. You can do this by hand on a separate piece of paper. To determine errors from a set of measured values, refer to the Reference Manual. Once you have formulas for \delta(T^2) and \delta(g) calculate \delta(T^2) and \delta(g) only for your first set of measurements.

a.   Note: both the period and length have an uncertainty, which needs to be considered with the error propagation.

4.   Next, put your first set of values into the Excel sheet provided for this lab, which has a worksheet titled ‘PART C.’ This worksheet will calculate the values of g, T^2 and their uncertainties given the input data.

5.   Check that what you calculated by hand for the FIRST set of measurements matches what is in the spreadsheet. Before moving on, show the TA your formula for \delta(T^2), and \delta(g). Ensure that your calculation for the FIRST set of values matches what is in the spreadsheet.

CHECKPOINT:

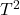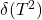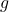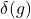(Ask the TA to check your sample calculation for T^2, \delta(T^2), g, and \delta(g) for the first set of values only)

6.   Fill in the rest of your data from the Results section into the “Part C” worksheet on Excel. As you fill in your data for length l, error in length \delta(l), time for 10 swings, error in time \delta(t), period T, and error in period squared \delta(T^2), the worksheet will automatically calculate; period squared T^2, the gravitational constant g, and the error in gravitational constant \delta(g), for each of the given values.

a.   Once you have filled in your Excel worksheet, it will provide a graph of T^2 as a function of l, calculate the average value of g from all the entries in your “Gravitational constant” column, and the average error in g from your “Error in gravitational constant”. According to the theory, the graph of T^2 as a function of l should give a straight line through the origin with a slope of 4\pi^2/g.

7.   Determine the trendline for this data on the T^2 versus l plot and report the equation of best fit on the graph.

a.   To add a trendline equation to your graph in Excel, right click on any data point in your graph (this will highlight them all), and then select “Format Trendline” from the drop-down menu.

b.   In the pop-up window, under “Options” select “Display Equation on Chart”. Use the slope of this equation to determine a value for g. Note: If you update your data, you will need to re-add the trendline equation to your chart.

CHECKPOINT:

(Ask the T.A. to check your plots)

***How to calculate g from the slope of the line of best fit.*** From Equation (2), we can write the period squared as a function l by T^2 = (\frac{4\pi^2}{g})l. When we observe the graph of T^2 versus l, we can see that the line of best fit is linear for the data. What that means is that we can relate the slope of our line of best fit, to Equation (2), and calculate a value for g from that line of best fit i.e.

slope for line of best fit = \frac{4\pi^2}{g}

Question 7.

Compare the average value of g  you obtained in the table for Part C, to the accepted value of g ~(9.81 m/s^2). Calculate the percent difference between experimental and theoretical values g  (see hint below). Does the average error in g that you calculated account for this difference? List some reasons why your value of  would have been different from the accepted value of g , regardless of what you calculated.

Hint: To calculate the percent difference between two values, A and B, use the following formula:

\frac{\|A-B\|}{(A+B/2)}*100\%

If the answer is \le 10\%, then you may conclude that A=B within 10% uncertainty.

 

 

Question 8.

Record the g value that you calculated from the line of best fit in your graph in Part C. Is your result for g in agreement with the accepted value within uncertainty?  Use the average value of uncertainty from your table in Part C as your uncertainty for g. Provide details, and if necessary, give plausible reasons for any disagreement.

 

License

Physics 1D03 Lab Manual Copyright © by nejatsm. All Rights Reserved.

Share This Book