Introduction

Dipole potential approximation

An electric dipole is a pair of opposite charges, and , separated by a distance (see Figure 1). When dealing with dipoles, we often consider a quantity called the dipole moment, . This is a vector that points from the negative to the positive charge and has a magnitude of .

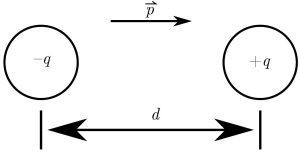
Figure 1: Schematic of an electric dipole.

An electric dipole creates an electric potential that is exactly equal to the sum of the potentials from the two charges:

(1)  

(2)  

A simpler form for this potential can be derived using approximations ^[1], leading to:

(3)  

Here, is the (approximate) electric potential at some point of interest , is Coulomb’s constant (), is the magnitude of the dipole moment, is the angle between the vector dipole moment and the vector direction to the point of interest, and is the distance from the point at the centre of the dipole to the point of interest. The values and are the distances from the positive and negative charges, respectively, to the point . Figure 2  shows how the coordinates, and , are measured relative to the dipole.

This approximation in Equation (3) is accurate when the potential is measured at distance much farther than the separation between the charges. In this case, this is true when . Note that the opposite is true: the potential calculated with Equation (3) when near the dipole can be very different from the exact potential (Equation 1).

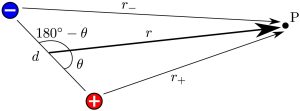
Figure 2: A diagram showing the relationship between the location of the dipole charges and the the point of interest P, where the electric potential (Eq. 3) is measured. The various distances and angles referenced in the main text are labelled.

Simulation software & hypotheses

In this experiment, you will be using an online simulation of the potential around an electric dipole to explore how closely Equation (3) represents the true potential. The simulation calculates the true potential by directly adding the potentials of the two charges together (using Equation (1) ), quickly doing the tedious sums for us. This illustrates how simulations are laboratories that let us explore physical theories, just like a physical lab with meter sticks and sensors.

Specifically, you will be making direct measurements of the exact potential from the dipole at increasing distances r from the charges. Reread the previous section carefully, and consider an appropriate hypothesis for this experiment that involves exploring how well Equation (3) will approximate the potential measured from the simulation. Do you expect Equation (3) to work well under all conditions?

        Refer to Section 2.4 of the reference material manual for more details on writing hypotheses, and think back on previous experiments as examples too.