Machine Learning
Machine learning is a subfield of computer science and mathematics that studies algorithms that improve their performance, or “learn”, or adapt, with experience and utilization of data. The algorithm “learn” patterns and features in the data that allow it to classify, cluster, or otherwise interpret the data. Machine learning, although distinct from artificial intelligence, has a connection to the latter field. In the context of the digital humanities, machine learning algorithms are adaptive algorithms that improve their performance through the data on which they act, in combination with specialized optimization (“learning”) approaches. Machine learning algorithms use sample data, called training data, as their input to generate a mathematical model for prediction, classification, or decision making. The resulting model is not programmed to make these predictions, classifications, or decisions. These capabilities emerge from the model based only on the training data.
The performance of machine learning algorithms depends on the availability of a large amount of training data. Consequently, machine learning has gained popularity because of the availability of large amounts of data through social media, the Web, sensors, and ubiquitous computing, thereby resulting in improved performance.
There are several classes of machine learning algorithms, or models. In supervised learning models, training data are labeled. The algorithm self-adapts to generate a model that maps the input training data to the output label. The goal is that the model generalizes. That is, the model will produce the correct output label given new, “unseen” input that was not included in the training data. Consequently, supervised learning is used for classification and prediction tasks.
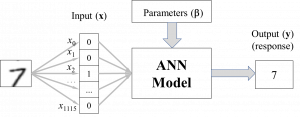
Artificial neural networks (ANNs) are examples of supervised machine learning. ANNs are models inspired by the nexus of interconnected neurons in the human brain. One well-known application is recognition of handwritten characters. The ANN is presented with a large number of images of these characters, usually represented as a list of binary values from the pixels of an image.
For instance, an image of a character that has size 31 x 36 (31 rows and 36 columns) can be input into the network as a list of 1,116 binary values, indicating whether a pixel contains the character or background. The label for that image is the character the image represents. For example, and image of a handwritten “7” character would have the label 7. A large number of images of handwritten characters for each represented character and their associated labels are used as training data. If the ANN has been trained properly, then an image of a character not in the training data (for example, a “7” character written by a person whose handwriting was not used to train the network) would result in the correct label for that character, 7 in this case, as shown below. Each image is represented by 1,116 pixels, numbered from 0 to 1,115.
Although the mathematical ideas and algorithms employed in training ANNs are complicated, the main idea is straightforward. Training is performed iteratively, in discrete steps, often called generations. Part of human supervision consists of selecting the maximum number of generations used to train the network. The ANN is essentially a large system of equations that transform the input data into an output – in this case, the labels. In the initialization step, the network is initialized with some parameters and weights for each input value. It is then presented with labeled training data. A single generation of ANN training can be described as follows. The ANN uses its system of equations and parameters to compute an output value from the input. This output value is then compared to the label associated with the input data. This process proceeds for all input data. The error between the correct labels provided in training and the outputs generated by ANN is calculated. The network weights are then modified through a mathematical process known as optimization. Many different optimization methods exist, and some methods are particularly well-suited for ANN training. After the weights have been adjusted, a new generation begins. The same training data are then re-applied to the network with the labels, as was the case in the first generation. The errors between the correct labels and ANN output for all the training samples are again calculated, and the weights are re-adjusted according to the optimization process. The entire procedure continues until the maximum number of generations selected by the user has been reached, or until the error falls below some tolerance level, in which case the error is sufficiently small to be considered acceptable. This tolerance level is also determined by the user based on the application.
A potential problem in unsupervised learning is overfitting, where the ANN “memorizes” the input training data. In this case, the mapping from input to output is overly “tight” and does not allow interpolation of values outside the training data. Consequently, the ANN does not generalize properly. Training ANNs must therefore proceed cautiously to produce a high accuracy model that can generalize and that does not result in overfitting. ANNs are relatively straightforward to train and have many classification applications in the digital humanities.
Unsupervised learning is another machine learning model. It also uses data for self-adaptation, but, unlike supervised learning, the data are not labeled. The purpose of unsupervised learning is for the machine learning algorithm to discover patterns, anomalies, and/or other interesting features in the input data, based only on those data, without a human user pre-specifying those patterns, anomalies, or features. In most cases, the user does not have a well-formed idea of what may be found in the data for a variety of reasons. The data may be excessively large, heterogeneous, or complex, for example, and, as a result, machine learning is employed to uncover what may not be evident or obvious to users. Two of the main applications of unsupervised learning are clustering and anomaly detection. In clustering, data, possibly heterogeneous, complex, and high-dimensional, are placed into groups, or clusters, based only on the characteristics of the data. Although clustering is unsupervised, a human user must usually specify the number of clusters. In anomaly detection, the unsupervised model “learns” the “typical” features and characteristics a dataset and determines whether new data differ significantly from those typical features of other data in the dataset.
Implementations of machine learning algorithms and ANNs are found in all major programming languages. Many Python and R libraries and packages for machine learning are available.
Machine learning approaches are used to analyze and to gain insights into voluminous data sets that are often high-dimensional and heterogenous. Consequently, these approaches are increasingly employed in the digital humanities to analyze and explore large volumes and corpora of text, images, 3D models of cultural artifacts, archival data, and other resources. However, the problem of interpretability is particularly relevant for humanities scholarship (Dobson, 2021). The notion of interpretability is not fully defined, but some researchers equate interpretability with “understandability” or “intelligibility”, which is the degree to which human users can understand how the models. Understandable models are described as transparent, in contrast to incomprehensible models, called black box models (Lipton, 2018). The model itself, its assumptions, and the processes by which it makes decisions or produces results must be clear and analyzable. Otherwise, the outputs produced by the model may be misleading or untrustworthy. Related to interpretability is transparency, where each input, parameter, and calculation can be intuitively explained, thereby providing the model with the property of intelligibility (Lipton, 2018). For simple models, such as linear regression (described in more detail below), as the number of variables and interactions among them increase, complexity correspondingly increases. With highly complex non-linear models, such as ANNs, the results may be too complicated, and therefore not comprehensible. Furthermore, the features that are ultimately used by machine learning models – either engineered by human users for the training data, or the features that the algorithm itself generates from mathematical transformations of the original data – may not have direct or intuitive correspondence to that original data. Because the processes by which these models produced their results cannot generally be understood, these algorithms are often termed as black box models, as described above.
One way to address interpretability is by finding new ways to explain the black box models, and to clarify its internal workings. However, another way is simply to use simpler models, or to design techniques that are interpretable in the first place. There are an increasing number of techniques that can be used to build interpretable models with high accuracy, beyond enhancements of less complex regression methods. These new methods incorporate domain knowledge – a key component in humanities work – and new, innovative optimization methods. Recall that machine learning models “learn” and adapt through an optimization process.
However important simple, robust, and accurate models are for interpretability and human understanding of the model, at present, these simpler, interpretable models are still less performant in terms of accuracy than black box models. For instance, ANNs, which are highly nonlinear black box algorithms, outperform other techniques for many applications, such as image recognition and analysis. In a highly cited article, machine learning researcher Zachary Lipton argues that “interpretability” itself is not well defined, and that different researchers mean different things when invoking the concept. He also argues against the notion that “simple” models are more interpretable than black box techniques (Lipton, 2018). In light of this, there is currently a trade-off between accuracy and interpretability. Consequently, the benefits of the newer modeling techniques with a higher degree of interpretability need to be weighed against a potential loss in accuracy. However, to address concerns over interpretability, simple, yet highly accurate models should still be developed, and if the less complex models, such as regression, produces the desired results, then replacing them with less interpretable black box models may not be warranted (see, From Exploring to Building Accurate Interpretable Machine Learning Models for Decision-Making: Think Simple, not Complex).

