"

11 Rational Exponents

 

* For  n \in \mathbb{N}=\{ 1,2,\ldots \},  the principal n^{th}  root of  x ,  is defined  by :

\qquad\bullet   If n is odd 

    \[\qquad \qquad y= x^{1/n}\qquad \Longleftrightarrow \qquad x=y^n.\]

 

\qquad\bullet   If n is even 

 

    \[ \qquad \left\|\begin{matrix} y= x^{1/n} \qquad & \hbox{ if } \quad x > 0 \qquad & \hbox{ with }\quad y= x^{1/n}\quad \Longleftrightarrow \quad x=y^n \\ \\ 0\qquad & \hbox{ if } \quad x=0 & \\ \\ \hbox{ not defined }\qquad &\hbox{ if }\quad x < 0 \qquad & \end{matrix}\right. \]

 

** \quad x^{m/n} \quad is defined by : \quad x^{m/n} =\Big( x^{1/n} \Big)^m\quad provided \quad x^{1/n} \quad is real.
    

    \[ \quad x^{-m/n} =\displaystyle{ \frac{1}{ x^{m/n} } } \]

 

    \[ \quad \Big(x^n\Big)^{1/n} = \left\{\begin{matrix} x \qquad & \hbox{ if } \quad n \quad \hbox{ is odd } \\ \\ |x|\qquad & \hbox{ if } \quad n \quad\hbox{ is even } \end{matrix}\right. \]

 

Watch a Video


View on YouTube

 

Show Examples

 

Exercise 1

 

Show/Hide Solution.

Using laws of exponents, we have

    \[t^{\frac{1}{{4}} } t^{{7}} = t^{\frac{1}{{4}}+({7}) } = t^{\frac{1 + ({4}) ({7}) }{{7}} }= t^{\frac{{29}}{{7}} }.\]

 

 

Exercise 2

 

Show/Hide Solution.

Using laws of exponents, we have

    \[ \Big( {-6} y^{\frac{{-2}}{{5}} } \Big)\Big( {2} y^{\frac{{4}}{{3}} }\Big) \) \(= ({-6}) . ({2}) y^{ \frac{{-2}}{{5}} +\frac{{4}}{{3}} } \) \( ={-12} y^{ \frac{ ({-2}) ({3}) + ({5}) ({4}) }{({5}) ({3}) } }= {-12} y^{\frac{{14}}{{15}} }. \]

 

 

Exercise 3

 

Show/Hide Solution.

Using laws of exponents, we have

\displaystyle{\Big( \frac{x^{{15}} y}{ y^6} \Big)^{{3}/{5}} }

=\displaystyle{\Big( \frac{x^{{15}} }{ y^{{6} -1 }} \Big)^{{3}/{5}} = \frac{ (x^{{15}})^{{3}/{5}} }{(y^{{6} -1 })^{{3}/{5}} } }

=\displaystyle{\frac{ x^{({15}) ({3}/{5} ) } }{ y^{({6}-1) ({3}/{5} ) } } }

= \displaystyle{\frac{x^{{9}} }{ y^{ {3} } } }

 

 

Exercise 4

 

Show/Hide Solution.

Using laws of exponents, we have

\displaystyle{\Big( \frac{ {4} x^{ -{8}} }{ {5}y^{-{5} }} \Big)^{-1} }
=\displaystyle{\frac{1}{\Big( \frac{ {4} x^{ -{8}} }{{5} y^{-{5} } }\Big)} = \frac{ {5} y^{-{5} }}{{4} x^{ -{8}}} = \frac{ {5} }{{4} }. \frac{( y^{{5} })^{-1}}{(x^{ {8}})^{-1}} }
= \displaystyle{ \frac{ {5} }{{4} }. \Big( \frac{ y^{{5} }}{ x^{ {8}} } \Big)^{-1} }= \displaystyle{\frac{{5}}{{4}}. \Big( \frac{ x^{ {8} } }{ y^{{5} } } \Big)} = \displaystyle{ \frac{ {5} x^{{8}} }{ {4} y^{{5} } } } .

 

 

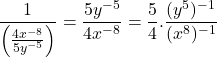
Exercise 5

 

Show/Hide Solution.

Using laws of exponents, we have

\displaystyle{\frac{ \big(y^{{6}} z^{-{2}}\big)^{1/{2}}}{ \big( y^{-{3} } z^{{4}}\big)^{1/{4}} } = \displaystyle{ y^{ {6}/{2} + {3}/{4} } z^{ -{2}/{2} - {2}/{2} } = \frac{ y^{ {15}/{4} } }{z^2} }

 

 

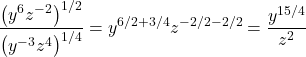
Exercise 6

 

Show/Hide Solution.

Using laws of exponents, we have

\displaystyle{ \big( x^{-{12}} y^{-{9}}z^{{6}}\big)^{-{2}/{3}} }

=\displaystyle{ \big( x^{-{12}}\big)^{-{2}/{3}} } . \displaystyle{ \big(y^{-{9}}\big)^{-{2}/{3}} } .\displaystyle{ \big( z^{{6}}\big)^{-{2}/{3}} }

=\displaystyle{ \big( x^{(-{12})(-{2}/{3})}\big) } . \displaystyle{ \big(y^{(-{9})(-{2}/{3})}\big) } .\displaystyle{ \big( z^{({6})(-{2}/{3})}\big) } = \displaystyle{ \frac{ x^{ {8} } y^{6}}{ z^{{4}} } }.

 

License

Icon for the Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License

Guide to Precalculus Review Copyright © 2025 by Samia CHALLAL is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, except where otherwise noted.

Share This Book