13 Radical Expressions
The nth radical is defined by : ![]()
![]()
A conjugate expression for 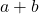 is the expression
is the expression 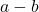 .
.
For rationalizing an expression, we multiply it by its conjugate.
For rationalizing an expression, we multiply it by its conjugate.
Exercise 1
Show/Hide Solution.
We have
![]()
Exercise 2
Show/Hide Solution.
We have
![]()
Exercise 3
Show/Hide Solution.
We have
![]()

