30 Parabola
A quadratic function ![]() can be expressed in the standard form
can be expressed in the standard form
![]()
by completing the square.
The graph of ![]() is a parabola with vertex
is a parabola with vertex ![]() .
.
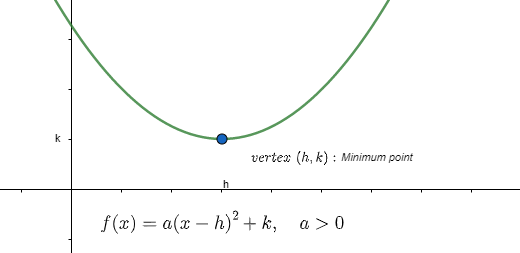
![]() If
If ![]() , then
, then
![]() the parabola opens upward and
the parabola opens upward and
![]() the minimum value of
the minimum value of ![]() is
is ![]()
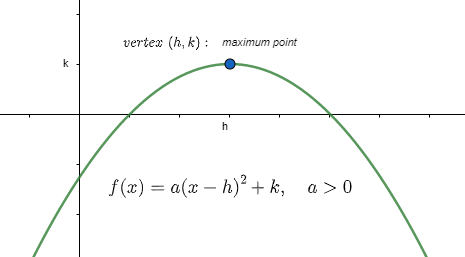
![]() If
If ![]() , then
, then
– the parabola opens downward and
– the maximum value of ![]() is
is ![]()
Exercise 1
Show/Hide Solution.
The equation of the quadratic function in its standard form is :
![]()
![]()
So,
![]() the vertex is :
the vertex is : ![]()
![]() maximum value is
maximum value is ![]() .
.
Set ![]() , then
, then ![]() . Hence there is no
. Hence there is no ![]() -intercepts.
-intercepts.
Set ![]() , then
, then ![]() . Hence
. Hence ![]() is the
is the ![]() -intercept.
-intercept.
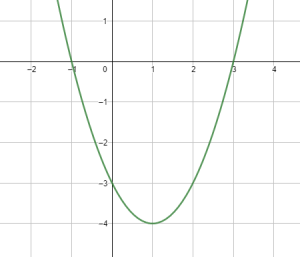
Exercise 2
Show/Hide Solution.
Set ![]() , then
, then ![]() . Hence
. Hence ![]() or
or ![]() are the
are the ![]() -intercepts.
-intercepts.
Set ![]() , then
, then ![]() . Hence
. Hence ![]() is the
is the ![]() -intercept.
-intercept.
The equation of the quadratic function in its standard form is :
![]()
So,
![]() the vertex is :
the vertex is : ![]()
![]() the minimum value is –
the minimum value is –![]() .
.

