"

25 Circles

A circle with center  P_0 (x_0, y_0)  and radius r>0 is the set of all points P(x,y) in the plane  \mathbb{R}^2 that are at the distance r from P_0.

The equation of this circle is obtained

    \[ \|P_0P\| = r \quad \Longleftrightarrow \quad \|P_0P\|^2 = r^2 \quad \Longleftrightarrow \quad (x-x_0)^2 + (y-y_0)^2 = r^2.\]

The unit circle is the cercle with center (0,0) and radius 1, described by the equation:

    \[x^2 + y^2 =1.\]

 

Watch a Video


View on YouTube

 

Show Examples

 

 

Exercise 1

 

Show/Hide Solution.

The radius is equal to the  length of the line segment joining the center and the intersection point with the x-axis  is (5,0). Using the distance formula, we obtain

r= \displaystyle{ \sqrt{ ( {5} - ( {5}) )^2 + ( {-2} -( {0}))^2} = |{-2}|= {2} }

The equation of the circle  is given by :

\displaystyle{ \Big( x-( {5} ) \Big)^2 + \Big( y- ({-2} ) \Big)^2 ={4} }

 

Exercise 2

 

Show/Hide Solution.

By completing the squares, we obtain:

(x -{2})^2 - ({2})^2 + (y+{5})^2 - (-{5})^2 = {-16}
\quad \Longleftrightarrow \quad (x -{2})^2 + (y+{5})^2 = {-16} + ({2})^2 + ({5})^2= {13}

The center is the point ({2}, {-5}) and the radius is R=\sqrt{13}.

 

Exercise 3

 

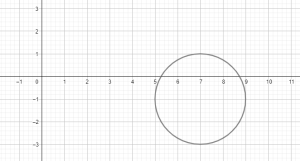
Show/Hide Solution.

The coordinates of the center are ({7}, {-1}).

The equation of the circle is given by :

\displaystyle{ \Big( x - (7) \Big)^2 + \Big( y-{(-1)} \Big)^2 = {2^2} }\quad   or \quad (x-7)^2 +(y+1)^2 =4.

License

Icon for the Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License

Guide to Precalculus Review Copyright © 2025 by Samia CHALLAL is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, except where otherwise noted.

Share This Book