9 Factoring
Some factoring forms
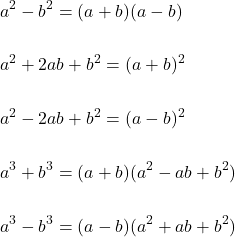
How to factor a polynomial?
- remove a common factor
- factor by grouping
- use special factoring forms.
Exercise 1
Show/Hide Solution.
![]()
![]()
![]() .
.
Exercise 2
Show/Hide Solution.
Set ![]() . We have
. We have
![]()
![]()
![]()
We used the identity : ![]() .
.
Exercise 3
Show/Hide Solution.
We factor the expression by regrouping terms.
![]()
![]()
![]()
![]()
![]()
Thus the common factor is: ![]() .
.
Exercise 4
Show/Hide Solution.
We apply the identity: ![]() .
.
![]()
Exercise 5
Show/Hide Solution.
We use the method of completing the square. We have
![]()
We used the identity : ![]() .
.
For ![]() , we can use the same method or the method of determinant.
, we can use the same method or the method of determinant.
We have ![]() and the roots are
and the roots are
![]()
Thus ![]()
Hence, the common factor is : ![]() .
.

