6.2 Frequency Distribution and Histograms
Learning Objectives
- Create and interpret frequency tables.
- Display data using a histogram.
- Analyze and interpret data presented in a graph.
Frequency
Twenty students were asked how many hours they worked per day. Their responses, in hours, are recorded in the table below:
| 5 | 6 | 3 | 3 | 2 | 4 | 7 | 5 | 2 | 3 |
| 5 | 6 | 5 | 4 | 4 | 3 | 5 | 2 | 5 | 3 |
The following table lists the different data values in ascending order and their frequencies.
| Data Value | Frequency |
|---|---|
| [latex]2[/latex] | [latex]3[/latex] |
| [latex]3[/latex] | [latex]5[/latex] |
| [latex]4[/latex] | [latex]3[/latex] |
| [latex]5[/latex] | [latex]6[/latex] |
| [latex]6[/latex] | [latex]2[/latex] |
| [latex]7[/latex] | [latex]1[/latex] |
A frequency is the number of times a value of the data occurs. According to the table, there are three students who work two hours, five students who work three hours, and so on. The sum of the values in the frequency column is 20, which is the total number of students included in the sample.
A relative frequency is the ratio (fraction or proportion) of the number of times a value of the data occurs in the set of all outcomes to the total number of outcomes. To find the relative frequencies divide each frequency by the total number of students in the sample–in this case20. Relative frequencies can be written as fractions, percents, or decimals. The sum of the values in the relative frequency column is 1 or 100%.
| Data Value | Frequency | Relative Frequency |
|---|---|---|
| [latex]2[/latex] | [latex]3[/latex] | [latex]\displaystyle\frac{3}{20}=0.15[/latex] |
| [latex]3[/latex] | [latex]5[/latex] | [latex]\displaystyle\frac{5}{20}=0.25[/latex] |
| [latex]4[/latex] | [latex]3[/latex] | [latex]\displaystyle\frac{3}{20}=0.15[/latex] |
| [latex]5[/latex] | [latex]6[/latex] | [latex]\displaystyle\frac{6}{20}=0.30[/latex] |
| [latex]6[/latex] | [latex]2[/latex] | [latex]\displaystyle\frac{2}{20}=0.10[/latex] |
| [latex]7[/latex] | [latex]1[/latex] | [latex]\displaystyle\frac{1}{20}=0.05[/latex] |
Cumulative frequency is the accumulation of the previous frequencies. To find the cumulative frequencies, add all of the previous frequencies to the frequency for the current row, as shown in the table below. The last entry of the cumulative frequency column is the number of observations in the data.
| Data Value | Frequency | Relative Frequency | Cumulative Frequency |
| [latex]2[/latex] | [latex]3[/latex] | [latex]0.15[/latex] | [latex]3[/latex] |
| [latex]3[/latex] | [latex]5[/latex] | [latex]0.25[/latex] | [latex]3+5=8[/latex] |
| [latex]4[/latex] | [latex]3[/latex] | [latex]0.15[/latex] | [latex]8 + 3 = 11[/latex] |
| [latex]5[/latex] | [latex]6[/latex] | [latex]0.30[/latex] | [latex]11 + 6 =17[/latex] |
| [latex]6[/latex] | [latex]2[/latex] | [latex]0.10[/latex] | [latex]17 + 2 = 19[/latex] |
| [latex]7[/latex] | [latex]1[/latex] | [latex]0.05[/latex] | [latex]19+ 1 = 20[/latex] |
Cumulative relative frequency is the accumulation of the previous relative frequencies. To find the cumulative relative frequencies, add all the previous relative frequencies to the relative frequency for the current row, as shown in the table below. The last entry of the cumulative relative frequency column is 1 or 100%, indicating that 100% of the data has been accumulated.
| Data Value |
Frequency | Relative Frequency | Cumulative Frequency | Cumulative Relative Frequency |
| [latex]2[/latex] | [latex]3[/latex] | [latex]0.15[/latex] | [latex]3[/latex] | [latex]0.15[/latex] |
| [latex]3[/latex] | [latex]5[/latex] | [latex]0.25[/latex] | [latex]8[/latex] | [latex]0.15 + 0.25 = 0.40[/latex] |
| [latex]4[/latex] | [latex]3[/latex] | [latex]0.15[/latex] | [latex]11[/latex] | [latex]0.40 + 0.15 = 0.55[/latex] |
| [latex]5[/latex] | [latex]6[/latex] | [latex]0.30[/latex] | [latex]17[/latex] | [latex]0.55 + 0.30 = 0.85[/latex] |
| [latex]6[/latex] | [latex]2[/latex] | [latex]0.10[/latex] | [latex]19[/latex] | [latex]0.85 + 0.10 = 0.95[/latex] |
| [latex]7[/latex] | [latex]1[/latex] | [latex]0.05[/latex] | [latex]20[/latex] | [latex]0.95 + 0.05 = 1.00[/latex] |
Because of rounding of the relative frequencies, the relative frequency column may not always sum to 1 or 100%, and the last entry in the cumulative relative frequency column may not be 1 or 100%. However, they each should be close to 1 or 100%. If all of the decimals are kept in the calculations, the relative frequency column will sum to 1 or 100% and the last cumulative relative frequency will be 1 or 100%.
Video: “Frequency Tables, Bar Charts, Pie Charts, Histograms, Grouped & Ungrouped Data Distributions” by Joshua Emmanuel [8:41] is licensed under the Standard YouTube License.Transcript and closed captions available on YouTube.
Histograms
A histogram is a visual display of a frequency chart. It consists of contiguous, vertical boxes with both a horizontal axis and a vertical axis. The horizontal axis is labelled with the classes or categories from the frequency chart. The vertical axis is labelled either frequency or relative frequency (or percent frequency or probability). The graph will have the same shape as either label on the vertical axis, but the scale on the vertical axis will be different. The histogram gives us the shape of the data, the center of the data, and the spread of the data.
Recall that the frequency is the number of times an observation falls into that particular class, and the relative frequency is the frequency for the class divided by the total number of data values in the sample. For example, if three students in Mr. Ahab’s English class of 40 students received from 90% to 100%, then the frequency of the 90% to 100% class is 3, and the relative frequency is [latex]\displaystyle{\frac{3}{40}=0.075}[/latex]. So, 7.5% of the students received between 90% and 100%.
To construct a histogram, first decide how many bars or intervals, also called classes, represent the data. For clarity, many histograms consist of 5 to 15 bars or classes, but the number of bars is determined by the person constructing the histogram. Choose a starting point for the first class that is less than the smallest data value. A convenient starting point is a lower value carried out to one more decimal place than the value with the most decimal places. For example, if the value with the most decimal places is 6.1 and this is the smallest value, a convenient starting point is 6.05. We say that 6.05 has more precision. If the value with the most decimal places is 2.23 and the lowest value is 1.5, a convenient starting point is 1.495. If the value with the most decimal places is 3.234 and the lowest value is 1.0, a convenient starting point is 0.9995. If all the data happen to be integers and the smallest value is 2, then a convenient starting point is 1.5. Also, when the starting point and other boundaries are carried to one additional decimal place, no data value will fall on a boundary.
A rule of thumb is to use a histogram when the data set consists of 100 values or more.
Video: Histograms | Applying mathematical reasoning | Pre-Algebra | Khan Academy by Khan Academy [6:8] is licensed under the Standard YouTube License.Transcript and closed captions available on YouTube.
Example 6.2.1
The following data are the heights (in inches to the nearest half inch) of 100 male semiprofessional soccer players. The heights are continuous data because height is a measurement.
| 60 | 64 | 64.5 | 66 | 66.5 | 67 | 67.5 | 69 | 70 | 71 |
| 60.5 | 64 | 64.5 | 66 | 66.5 | 67 | 67.5 | 69 | 70 | 71 |
| 61 | 64 | 64.5 | 66.5 | 66.5 | 67 | 67.5 | 69 | 70 | 72 |
| 61 | 64 | 66 | 66.5 | 67 | 67 | 68 | 69 | 70 | 72 |
| 61.5 | 64 | 66 | 66.5 | 67 | 67 | 68 | 69 | 70 | 72 |
| 63.5 | 64.5 | 66 | 66.5 | 67 | 67.5 | 69 | 69.5 | 70 | 72.5 |
| 63.5 | 64.5 | 66 | 66.5 | 67 | 67.5 | 69 | 69.5 | 70.5 | 72.5 |
| 63.5 | 64.5 | 66 | 66.5 | 67 | 67.5 | 69 | 69.5 | 70.5 | 73 |
| 64 | 64.5 | 66 | 66.5 | 67 | 67.5 | 69 | 69.5 | 70.5 | 73.5 |
| 64 | 64.5 | 66 | 66.5 | 67 | 67.5 | 69 | 69.5 | 71 | 74 |
The smallest data value is 60. Because the data with the most decimal places has one decimal (for instance, 61.5), we want our starting point to have two decimal places. Because the numbers 0.5, 0.05, 0.005, etc. are convenient numbers, use 0.05 and subtract it from 60, the smallest value, for the convenient starting point. Then the starting point is, then, [latex]60-0.05=59.95[/latex]. The largest value is [latex]74[/latex], so [latex]74 + 0.05 = 74.05[/latex] is the ending value.
Next, calculate the width of each bar or class interval. To calculate this width, subtract the starting point from the ending value and divide by the number of classes (you must decide how many classes you want). Suppose we want to have eight classes.
[latex]\displaystyle{\mbox{Class Width}=\frac{74.05-59.95}{8}=1.76}[/latex]
We will round up to two and make each bar or class interval two units wide. Rounding up to two is one way to prevent a value from falling on a boundary. Rounding to the next number is often necessary even if it goes against the standard rules of rounding. For this example, using 1.76 as the width would also work.
The boundaries for the classes are:
[latex]\begin{eqnarray*}59.95\\59.95+2&=&61.95\\61.95+2&=&63.95\\63.95+2&=&65.95\\65.95+2&=&67.95\\67.95+2&=&69.95\\69.95+2&=&71.95\\71.95+2&=&73.95\\73.95+2&=&75.95\end{eqnarray*}[/latex]
The heights 60 through 61.5 inches are in the first class 59.95–61.95. The heights that are 63.5 are in the second class 61.95–63.95. The heights that are 64 through 64.5 are in the third class 63.95–65.95. The heights 66 through 67.5 are in the fourth class 65.95–67.95. The heights 68 through 69.5 are in the fifth class 67.95–69.95. The heights 70 through 71 are in the sixth class 69.95–71.95. The heights 72 through 73.5 are in the seventh class 71.95–73.95. The height 74 is in the last class 73.95–75.95.
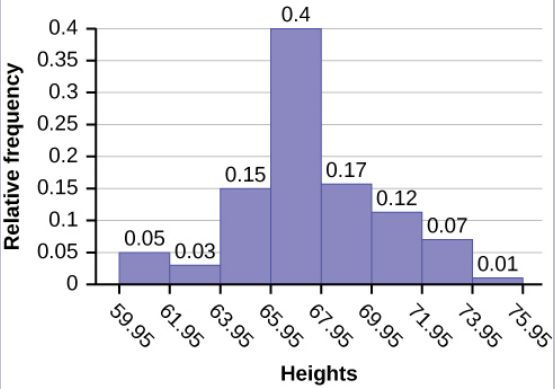
The following histogram displays the heights on the [latex]x[/latex]-axis and relative frequency on the [latex]y[/latex]-axis.
Image Description
The image is a histogram displaying the relative frequency of heights. The x-axis is labeled “Heights” with values ranging from 59.95 to 75.95. The y-axis is labeled “Relative frequency” with values ranging from 0 to 0.4. Each bar represents an interval of heights and their corresponding relative frequency values.
| Height Interval | Relative Frequency |
|---|---|
| 59.95 | 0.05 |
| 61.95 | 0.03 |
| 63.95 | 0.15 |
| 65.95 | 0.4 |
| 67.95 | 0.17 |
| 69.95 | 0.12 |
| 71.95 | 0.07 |
| 73.95 | 0.01 |
The highest bar is between 65.95 and 67.95, with a relative frequency of 0.4, indicating that this height range occurs most frequently in the data set. Other height intervals show varying lower frequencies.
Note
A guideline that is followed by some for the width of a bar or class interval is to take the square root of the number of data values and then round to the nearest whole number, if necessary. For example, if there are 150 values of data, take the square root of 150 and round to 12 bars or classes.
Try It
The following data are the shoe sizes of 50 male students. The sizes are continuous data since shoe size is measured. Construct a histogram and calculate the width of each bar or class interval. Suppose you choose six bars.
| 9 | 9 | 9.5 | 9.5 | 10 | 10 | 10 | 10 | 10 | 10 |
| 10.5 | 10.5 | 10.5 | 10.5 | 10.5 | 10.5 | 10.5 | 10.5 | 11 | 11 |
| 11 | 11 | 11 | 11 | 11 | 11 | 11 | 11 | 11 | 11 |
| 11 | 11.5 | 11.5 | 11.5 | 11.5 | 11.5 | 11.5 | 11.5 | 12 | 12 |
| 12 | 12 | 12 | 12 | 12 | 12.5 | 12.5 | 12.5 | 12.5 | 14 |
Solution
- Smallest value: [latex]9[/latex]
- Largest value: [latex]14[/latex]
- Convenient starting value: [latex]9 – 0.05 = 8.95[/latex]
- Convenient ending value: [latex]14 + 0.05 = 14.05[/latex]
- Class width: [latex]\displaystyle{\frac{14.05-8.95}{6}=0.85}[/latex]
The calculations suggest using [latex]0.85[/latex] as the width of each bar or class interval. You can also use an interval with a width equal to one.
Example 6.2.2
The following data are the number of books bought by 50 part-time college students at ABC College. The number of books is discrete data because books are counted.
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 1 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 |
| 2 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 |
| 3 | 3 | 3 | 3 | 3 | 3 | 3 | 4 | 4 | 4 |
| 4 | 4 | 4 | 5 | 5 | 5 | 5 | 5 | 6 | 6 |
Eleven students buy one book. Ten students buy two books. Sixteen students buy three books. Six students buy four books. Five students buy five books. Two students buy six books.
Because the data are integers, subtract 0.5 from 1, the smallest data value and add 0.5 to 6, the largest data value, to get the starting and ending points. Then the starting point is 0.5 and the ending value is 6.5.
Next, calculate the width of each bar or class interval. If the data are discrete and there are not too many different values, a width that places the data values in the middle of the bar or class interval is the most convenient. Because the data consist of the numbers 1, 2, 3, 4, 5, 6 and the starting point is 0.5, a width of one places the 1 in the middle of the interval from 0.5 to 1.5, the 2 in the middle of the interval from 1.5 to 2.5, the 3 in the middle of the interval from 2.5 to 3.5, the 4 in the middle of the interval from _______ to _______, the 5 in the middle of the interval from _______ to _______, and the _______ in the middle of the interval from _______ to _______ .
Solution:
- 3.5 to 4.5
- 4.5 to 5.5
- 6
- 5.5 to 6.5
Calculate the number of bars as follows:
[latex]\begin{eqnarray*}\frac{6.5-0.5}{\mbox{number of bars}}& = & 1 \end{eqnarray*}[/latex]
where 1 is the width of a bar. Therefore, the number of bars is 6.
The following histogram displays the number of books on the [latex]x[/latex]-axis and the frequency on the [latex]y[/latex]-axis.
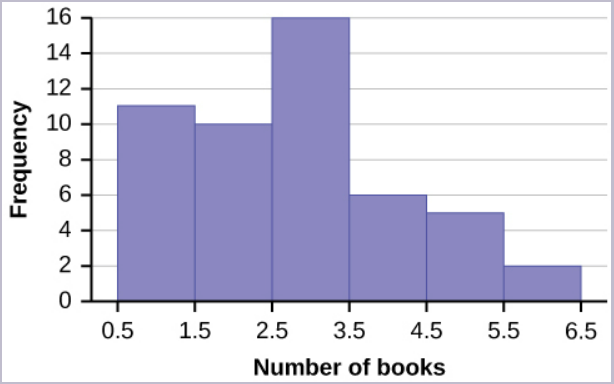
Image Description
The image is a histogram displaying the frequency of books read, divided into different number ranges. The x-axis is labelled “Number of books” and ranges from 0.5 to 6.5, with increments of 1. The y-axis is labelled “Frequency” and ranges from 0 to 16, with increments of 2.
Bars in the histogram represent the following data:
- From 0.5 to 1.5: Frequency is 10.
- From 1.5 to 2.5: Frequency is 12.
- From 2.5 to 3.5: Frequency is 16.
- From 3.5 to 4.5: Frequency is 5.
- From 4.5 to 5.5: Frequency is 3.
- From 5.5 to 6.5: Frequency is 2.
Video: How to Construct a Histogram in Excel using built-in Data Analysis by Joshua Emmanuel [1:59] is licensed under the Standard YouTube License.Transcript and closed captions available on YouTube.
Try It
The following data are the number of sports played by 50 student-athletes. The number of sports is discrete data because sports are counted.
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 |
| 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 |
| 2 | 2 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 |
Fill in the blanks for the following sentence. Because the data consist of the numbers 1, 2, 3, and the starting point is 0.5, a width of one places the 1 in the middle of the interval 0.5 to _____, the 2 in the middle of the interval from _____ to _____, and the 3 in the middle of the interval from _____ to _____.
Solution
- 1.5
- 1.5 to 2.5
- 2.5 to 3.5
Example 6.2.3
Using this data set, construct a histogram.
| Number of Hours My Classmates Spent Playing Video Games on Weekends | ||||
| 9.95 | 10 | 2.25 | 16.75 | 0 |
| 19.5 | 22.5 | 7.5 | 15 | 12.75 |
| 5.5 | 11 | 10 | 20.75 | 17.5 |
| 23 | 21.9 | 24 | 23.75 | 18 |
| 20 | 15 | 22.9 | 18.8 | 20.5 |
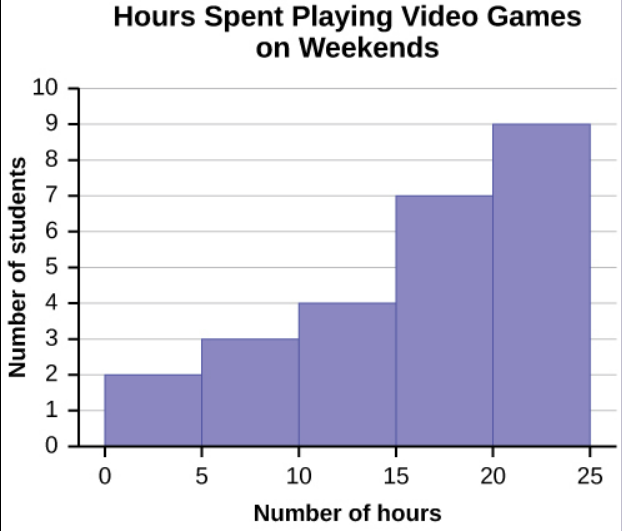
Image Description
The image is a histogram titled “Hours Spent Playing Video Games on Weekends.” It displays data on the number of students and the hours they spend playing video games during weekends. The x-axis represents the “Number of hours,” ranging from 0 to 25. The y-axis represents the “Number of students,” ranging from 0 to 10. The bars indicate the following data:
| Number of hours | Number of students |
|---|---|
| 0-5 | 2 |
| 5-10 | 3 |
| 10-15 | 4 |
| 15-20 | 6 |
| 20-25 | 9 |
Some values in this data set fall on boundaries for the class intervals. A value is counted in a class interval if it falls on the left boundary but not if it falls on the right boundary. Different researchers may set up histograms for the same data in different ways. There is more than one correct way to set up a histogram.
Attribution
“2.2 Histograms, Frequency Polygons, and Time Series Graphs” & “1.4 Frequency, Frequency Tables, and Levels of Measurement” in Introduction to Statistics by Valerie Watts is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.
