2.5: Chain Rule
There is one more type of function that we will want to know how to differentiate: composition. The Chain Rule will let us find the derivative of a composition. (This is the last derivative rule we will learn!)
Example 1
Find the derivative of [latex]y=\left(4x^3+15x\right)^2[/latex]
Answer:
This is not a simple polynomial, so we can’t use the basic building block rules yet. It is a product, so we could write it as [latex]y=\left(4x^3+15x\right)^2=\left(4x^3+15x\right)\left(4x^3+15x\right)[/latex] and then use the product rule. Or we could multiply it out and simply differentiate the resulting polynomial. Let's try do it the second way:
\[ \begin{align*}
y & = \left(4x^3+15x\right)^2\\
& = 16x^6+120x^4+225x^2\\
y' & = 96x^5+480x^3+450x
\end{align*} \]
Now suppose we want to find the derivative of [latex]y=\left(4x^3+15x\right)^{20}[/latex]. We could write it as a product with 20 factors and use the product rule, or we could multiply it out. But who wants to do that, do you?
We need an easier way, a rule that will handle a composition like this. The Chain Rule is a little complicated, but it saves us the much more complicated algebra of multiplying something like this out. It will also handle compositions where it wouldn't be possible to multiply it out.
The Chain Rule is a common place for students to make mistakes. Part of the reason is that the notation takes a little getting used to. And part of the reason is that students often forget to use it when they should. When should you use the Chain Rule? Almost every time you take a derivative.
Derivative Rules: Chain Rule
In what follows, [latex]f[/latex] and [latex]g[/latex] are differentiable functions where [latex]y = f(g(x))[/latex]. We could alternatively write [latex]y=f(u)[/latex] and [latex]u=g(x)[/latex].
Chain Rule (Leibniz notation)
\[\frac{dy}{dx}=\frac{dy}{du}\cdot\frac{du}{dx}\]
Notice that the [latex]du[/latex]’s seem to cancel. This is one advantage of the Leibniz notation - it can remind you of how the chain rule chains together.
Chain Rule (using prime notation)
\[\frac{d}{dx} f\left(g(x)\right) =f'\left(g(x)\right)\cdot g'(x)\]
Chain Rule (in words)
The derivative of a composition is the derivative of the outside (with the inside staying the same) TIMES the derivative of the inside.
I recite the version in words each time I take a derivative, especially if the function is complicated.
Video Demonstration
Compositions of Functions and the Chain Rule
© 2014 Eric Bancroft
Example 2
Find the derivative of [latex]y=\left(4x^3+15x\right)^2[/latex]
Answer:
This is the same one we did before by multiplying out. This time, let’s use the Chain Rule: The inside function is what appears inside the parentheses: [latex]4x^3+15x[/latex]. The outside function is the first thing we find as we come in from the outside - it’s the square function, [latex](\text{inside})^2[/latex].
In [latex]y=\left(4x^3+15x\right)^2[/latex], the inside function is [latex]4x^3+15x[/latex], which is then squared, so the square is the outside function.
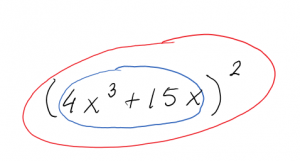
The derivative of this outside function is [latex](2\cdot\text{inside})[/latex]. Now using the chain rule, the derivative of our original function is [latex](2\cdot\text{inside})[/latex] times the derivative of the inside (which is [latex]12x^2+15[/latex]):
\[ y'=2\left(4x^3+15x\right)\left(12x^2+15 \right)\]
If you multiply this out, you get the same answer we got before. Hurray! Algebra works!
Example 3
Find the derivative of [latex]y=\left(4x^3+15x\right)^{20}[/latex].
Answer:
Now we have a way to handle this one. It’s the derivative of the outside times the derivative of the inside.

The outside function is [latex]\left(\text{inside}\right)^{20}[/latex], which has derivative [latex]20\left(\text{inside}\right)^{19}[/latex], so \[y'=20\left(4x^3+15x\right)^{19}\left(12x^2+15\right).\]
Example 4
Differentiate [latex]y=e^{x^2+5}[/latex].
Answer:
This isn’t a simple exponential function because the exponent is not simply the variable - it is another function (a polynomial). As a result, this is a composition of functions.
To determine the inside function and the outside function, analyze what happens to your variable. Here, our variable [latex]x[/latex] is first used in a polynomial, which is [latex]x^2+5[/latex]. This tells us that [latex]x^2+5[/latex] is the inside function. Then the polynomial is put into the exponent of [latex]e[/latex], so [latex]e^{\text{inside}}[/latex] is the outside function.
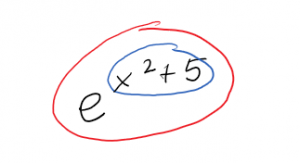
Now we can use the Chain Rule: We want the derivative of the outside times the derivative of the inside. The outside is the [latex]e[/latex] to the something function, so its derivative is the same thing. The derivative of what’s inside is [latex]2x[/latex]. So \[\frac{d}{dx}\left( e^{x^2+5} \right)= \left( e^{x^2+5} \right)\cdot (2x)\]
Example 5
The table gives values for [latex]f[/latex] , [latex]f'[/latex] , [latex]g[/latex], and [latex]g'[/latex] at a number of points. Use these values to determine [latex]( f \circ g )(x)[/latex] and [latex]( f \circ g ) '(x)[/latex] at [latex]x = -1[/latex] and 0.
| [latex]x[/latex] | [latex]f(x)[/latex] | [latex]g(x)[/latex] | [latex]f'(x)[/latex] | [latex]g'(x)[/latex] | [latex](f\circ g)(x)[/latex] | [latex](g\circ f)(x)[/latex] |
| -1 | 2 | 3 | 1 | 0 | ||
| 0 | -1 | 1 | 3 | 2 | ||
| 1 | 1 | 0 | -1 | 3 | ||
| 2 | 3 | -1 | 0 | 1 | ||
| 3 | 0 | 2 | 2 | -1 |
Answer:
[latex](f\circ g)(-1) = f\left(g(-1)\right)=f(3)=0[/latex]
[latex](f\circ g)(0) = f\left(g(0)\right)=f(1)=1\\[/latex]
[latex](f\circ g)'(-1) = f'\left(g(-1)\right)\cdot g'(-1)=f'(3)\cdot (0)=(2)(0)=0[/latex]
[latex](f\circ g)'(0) = f'\left(g(0)\right)\cdot g'(0)=f'(1)\cdot (2)=(-1)(2)=-2[/latex]
Video Demonstration
More Chain Rule Examples
© 2014 Eric Bancroft
Example 6
If 2400 people now have a disease, and the number of people with the disease appears to double every 3 years, then the number of people expected to have the disease in [latex]t[/latex] years is [latex]y=2400\cdot 2^{t/3}[/latex].
a. How many people are expected to have the disease in 2 years?
b. When are 50,000 people expected to have the disease?
c. How fast is the number of people with the disease expected to grow now and 2 years from now?
Answer:
a. In 2 years, [latex]y = 2400\cdot 2^{2/3} \approx 3,810[/latex] people.
b. We know [latex]y = 50,000[/latex], and we need to solve [latex]50,000 = 2400\cdot 2^{t/3}[/latex] for [latex]t[/latex].
\[
\begin{align*}
\frac{50000}{2400} & = 2^{t/3} \\
\Rightarrow&\ln\left(\frac{50000}{2400}\right) = \ln\left(2^{t/3}\right)\\
\Rightarrow&\ln\left(\frac{50000}{2400}\right) = \frac{t}{3}\cdot \ln(2)\\
\Rightarrow&t = \frac{3\ln\left(\frac{50000}{2400}\right)}{\ln(2)}\approx 13.14\text{ years}
\end{align*}
\]
Therefore we expect 50,000 people to have the disease about 13.14 years from now.
c. This is asking for [latex]\frac{dy}{dt}[/latex] when [latex]t =[/latex] 0 and 2 years. When we analyze [latex]y[/latex], we can see that the exponent of 2 is not simply the variable [latex]t[/latex], but a function of [latex]t[/latex] ([latex]t[/latex] divided by 3). Therefore, the function [latex]y=2^{t/3}[/latex] is a composition of functions and so, to find its derivative, we must use the chain rule. The inside function is [latex]\frac{1}{3}t[/latex] and the outside function is [latex]2^{\text{inside}}[/latex].
\[ \begin{align*}
\frac{dy}{dt} & = \frac{d}{dt}\left(2400\cdot 2^{t/3}\right) \\
& = 2400\cdot 2^{t/3}\cdot \ln(2)\cdot\frac{1}{3} \\
& \approx 554.5\cdot 2^{t/3}
\end{align*} \]
So, at [latex]t=0[/latex] the rate of growth of the disease is approximately [latex]554.5\cdot 2^0 \approx 554.5[/latex] people/year. In 2 years the rate of growth will be approximately [latex]554.5\cdot 2^{2/3} \approx 880[/latex] people/year.
Derivatives of Complicated Functions
You're now ready to take the derivative of some mighty complicated functions. But how do you tell what rule applies first? Work your way in from the outside – what do you encounter first? That’s the first rule you need. Use the Product, Quotient, and Chain Rules to peel off the layers, one at a time, until you’re all the way inside.
Example 7
Find [latex]\frac{d}{dx}\left( e^{3x}\cdot\ln(5x+7) \right)[/latex]
Answer: Let's first analyze the function.
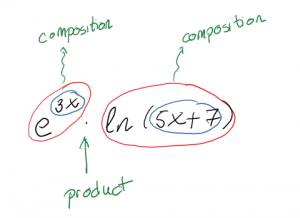
Loking at the whole expression, we see that this is a product of two compositions of functions. So we’ll need the Product Rule first. We’ll fill in the pieces we know, and then we can figure the rest as separate steps and substitute in at the end:
\[\frac{d}{dx}\left( e^{3x}\cdot\ln(5x+7) \right)=\left( \frac{d}{dx}\left( e^{3x}\right)\right)\cdot\ln(5x+7)+ e^{3x}\cdot \left(\frac{d}{dx}\left(\ln(5x+7) \right)\right)\]
Now as separate steps, we’ll find \[\frac{d}{dx}\left( e^{3x}\right)=3e^{3x} \quad \text{ (using the Chain Rule)}\] and \[\frac{d}{dx}\left(\ln(5x+7) \right)=\frac{1}{5x+7}\cdot 5 \quad \text{ (also using the Chain Rule)}.\]
Finally, to substitute these in their places:\[\frac{d}{dx}\left( e^{3x}\cdot\ln(5x+7) \right)=\left( 3e^{3x}\right)\cdot\ln(5x+7)+ e^{3x}\cdot \left(\frac{1}{5x+7}\cdot 5\right)\]
(We can stop here - we don't need to try to simplify any further.)
Example 8
Differentiate [latex]z=\left(\dfrac{3t^3}{e^t(t-1)}\right)^4[/latex]
Answer:
Don’t panic! As we look at the function, we can see that we have some complicated thing, raised to the power of 4. That tells us that we are dealing with a composition of functions: to find the value of the function, first the thing in the bracket gets calculated, then it is raised to the power of 4. So the inside function is what is inside the bracket. This tells us that we will have to use the chain rule. In order to use the chain rule, we will have to calculate the derivative of the outside function (power function) and the derivative of the inside function (the complicated thing).
Now, when we look at the inside function, we can see that it is a quotient, or a fraction, of two functions. This means we will have to use the Quotient Rule when we differentiate the inside function. This quotient is made of a polynomial in the numerator and a product of functions in the denominator, for which we will have to use the product rule.
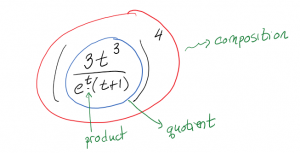 Step One: Use the Chain Rule. The derivative of the outside times the derivative of the inside:
Step One: Use the Chain Rule. The derivative of the outside times the derivative of the inside:
\[
\frac{dz}{dt}=\frac{d}{dt}\left(\frac{3t^3}{e^t(t-1)}\right)^4=4\left(\frac{3t^3}{e^t(t-1)}\right)^3\cdot \frac{d}{dt}\left(\frac{3t^3}{e^t(t-1)}\right)
\]
Now we’re one step inside, and we can concentrate on just the [latex]\frac{d}{dt}\left(\frac{3t^3}{e^t(t-1)}\right)[/latex]. This is the derivative of a quotient of two functions.
Step Two: Use the Quotient Rule. The derivative of the numerator is straightforward, so we can just calculate it. The derivative of the denominator uses product rule, so we'll leave it for now:
\[
\frac{d}{dt}\left(\frac{3t^3}{e^t(t-1)}\right)=\frac{\left( 9t^2 \right)\left( e^t(t-1) \right)-\left( 3t^3 \right)\left( \frac{d}{dt}\left( e^t(t-1) \right) \right)}{\left(e^t(t-1)\right)^2}
\]
Now we’ve gone one more step inside, and we can concentrate on just the denominator [latex]\frac{d}{dt}\left( e^t(t-1) \right)[/latex], which involves a product.
Step Three: Use the Product Rule: \[ \frac{d}{dt}\left( e^t(t-1)\right) = \left( e^t \right)(t-1)+\left( e^t \right)(1)\]
And now we’re all the way in - no more derivatives to take!
Step Four: Now it’s just a question of substituting back - be careful now!
\[
\frac{d}{dt}\left( e^t(t-1)\right) = \left( e^t \right)(t-1)+\left( e^t \right)(1)
\]
so
\[
\frac{d}{dt}\left(\frac{3t^3}{e^t(t-1)}\right)=\frac{\left( 9t^2 \right)\left( e^t(t-1) \right)-\left( 3t^3 \right)\left( \left( e^t \right)(t-1)+\left( e^t \right)(1) \right)}{\left(e^t(t-1)\right)^2}
\]
so
\[
\begin{align*}
\frac{dz}{dt}&=\frac{d}{dt}\left(\frac{3t^3}{e^t(t-1)}\right)^4\\\\
&=4\left(\frac{3t^3}{e^t(t-1)}\right)^3\cdot \left( \frac{\left( 9t^2 \right)\left( e^t(t-1) \right)-\left( 3t^3 \right)\left( \left( e^t \right)(t-1)+\left( e^t \right)(1) \right)}{\left(e^t(t-1)\right)^2} \right)
\end{align*}
\]
Phew!
What if the Derivative Doesn’t Exist?
Differentiable
We’ve been acting as if derivatives exist everywhere for every function. This is true for most of the functions that you will run into in this course. But there are some common places where the derivative doesn’t exist.
Remember that the derivative is the slope of the tangent line to the curve. That’s what to think about.
Where can a slope not exist? First of all, the slope can't exist where the function is not defined. So the derivative will not exist at values that are outside of the domain of the function.
Second, if the tangent line is vertical, it's slope is not defined, and so the derivative at the point that has a vertical tangent line will not exist.
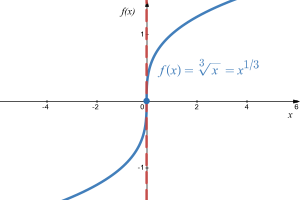
Example 9
Show that [latex]f(x)=\sqrt[3]{x}=x^{1/3}[/latex] is not differentiable at [latex]x = 0[/latex].
Answer:
At [latex]x=0[/latex], [latex]f(x)=0^{1/3}=0[/latex] and so the function is defined at 0.
Finding the derivative, we get [latex]f(x)=\frac{1}{3}x^{-2/3}=\frac{1}{3x^{2/3}}[/latex]. At [latex]x = 0[/latex], the derivative function is undefined.
From the graph, we can see that the tangent line to this curve at [latex]x = 0[/latex] is vertical with undefined slope, which is why the derivative does not exist at [latex]x = 0[/latex].
We could also have a case where the tangent line does not exist at all. Here are a couple of examples when this happens:
- If there is a sharp corner (cusp) in the graph, the derivative will not exist at that point because there is no well-defined tangent line (a teetering tangent, if you will).
- If there is a discontinuity in the graph (a jump, a break, a hole in the graph, or a vertical asymptote), the tangent line will be different on either side and the derivative will not exist at that point .
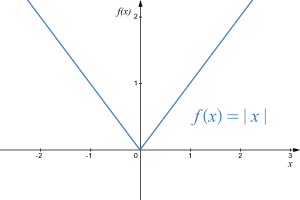
Example 10
Show that [latex]f(x)=|x|[/latex] is not differentiable at [latex]x = 0[/latex].
Answer:
On the left side of the graph, the slope of the line is -1. On the right side of the graph, the slope is +1. There is no well-defined tangent line at the sharp corner at [latex]x = 0[/latex], so the function is not differentiable at that point.
Video Demonstration
When is a function not differentiable?
© 2014 Eric Bancroft
Section Exercises
Work on the following exercises. Discuss your solutions with your peers and/or course instructor.
Section 2.5 Exercises - Chain Rule

