8.6 Hypothesis Tests for a Population Proportion
LEARNING OBJECTIVES
- Conduct and interpret hypothesis tests for a population proportion.
Some notes about conducting a hypothesis test:
- The null hypothesis [latex]H_0[/latex] is always an "equal to." The null hypothesis is the original claim about the population parameter.
- The alternative hypothesis [latex]H_a[/latex] is a "less than," "greater than," or "not equal to." The form of the alternative hypothesis depends on the context of the question.
- The form of the alternative hypothesis tells us if the test is left-tail, right-tail, or two-tail. The alternative hypothesis is the key to conducting the test and finding the correct [latex]p-\text{value}[/latex].
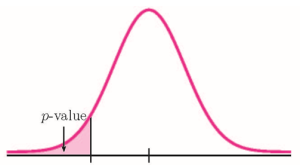
- If the alternative hypothesis is a "less than", then the test is left-tail. The [latex]p-\text{value}[/latex] is the area in the left-tail of the distribution.
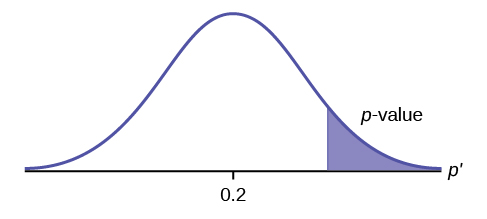
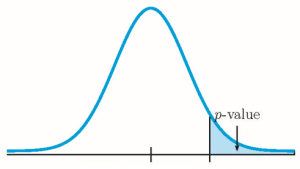
- If the alternative hypothesis is a "greater than", then the test is right-tail. The [latex]p-\text{value}[/latex] is the area in the right-tail of the distribution.
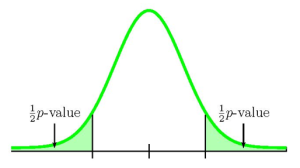
- If the alternative hypothesis is a "not equal to", then the test is two-tail. The [latex]p-\text{value}[/latex] is the sum of the area in the two-tails of the distribution. Each tail represents exactly half of the [latex]p-\text{value}[/latex].
- Think about the meaning of the [latex]p-\text{value}[/latex]. A data analyst (and anyone else) should have more confidence that they made the correct decision to reject the null hypothesis with a smaller [latex]p-\text{value}[/latex] (for example, [latex]0.001[/latex] as opposed to [latex]0.04[/latex]) even if using a significance level of [latex]0.05[/latex]. Similarly, for a large [latex]p-\text{value}[/latex] such as [latex]0.4[/latex], as opposed to a [latex]p-\text{value}[/latex] of [latex]0.056[/latex] (a significance level of [latex]0.05[/latex] is less than either number), a data analyst should have more confidence that they made the correct decision in not rejecting the null hypothesis. This makes the data analyst use judgment rather than mindlessly applying rules.
- The significance level must be identified before collecting the sample data and conducting the test. Generally, the significance level will be included in the question. If no significance level is given, a common standard is to use a significance level of [latex]5\%[/latex].
EXAMPLE
EXAMPLE
Suppose the hypotheses for a hypothesis test are:
[latex]\begin{eqnarray*}H_0:&&p=50\%\\H_a:&&p\neq50\%\end{eqnarray*}[/latex]
Because the alternative hypothesis is a [latex]\neq[/latex], this is a two-tail test. The [latex]p-\text{value}[/latex] is the sum of the areas in the two tails of the distribution. Each tail contains exactly half of the [latex]p-\text{value}[/latex].
EXAMPLE
Suppose the hypotheses for a hypothesis test are:
[latex]\begin{eqnarray*}H_0:&&p=10\%\\H_a:&&p\lt10\%\end{eqnarray*}[/latex]
Because the alternative hypothesis is a [latex]\lt[/latex], this is a left-tail test. The [latex]p-\text{value}[/latex] is the area in the left-tail of the distribution.
Conducting a Hypothesis Test for a Population Proportion
Follow these steps to perform a hypothesis test for a population proportion:
- Write down the null and alternative hypotheses in terms of the population proportion [latex]p[/latex]. Include appropriate units with the values of the proportion.
- Use the form of the alternative hypothesis to determine if the test is left-tailed, right-tailed, or two-tailed.
- Collect the sample information for the test and identify the significance level.
- Find the [latex]p-\text{value}[/latex] (the area in the corresponding tail) for the test using the appropriate distribution:
- If [latex]n\times p\geq 5[/latex] and [latex]n\times(1-p)\geq 5[/latex], use the normal distribution with [latex]\displaystyle{z=\frac{\hat{p}-p}{\sqrt{\frac{p\times(1-p)}{n}}}}[/latex].
- If one of [latex]n\times p\lt 5[/latex] or [latex]n\times(1-p)\lt 5[/latex], use a binomial distribution.
- Compare the [latex]p-\text{value}[/latex] to the significance level and state the outcome of the test.
- If [latex]p-\text{value}\leq\alpha[/latex], reject [latex]H_0[/latex] in favour of [latex]H_a[/latex].
- The results of the sample data are significant. There is sufficient evidence to conclude that the null hypothesis [latex]H_0[/latex] is an incorrect belief and that the alternative hypothesis [latex]H_a[/latex] is most likely correct.
- If [latex]p-\text{value}\gt\alpha[/latex], do not reject [latex]H_0[/latex].
- The results of the sample data are not significant. There is not sufficient evidence to conclude that the alternative hypothesis [latex]H_a[/latex] may be correct.
- If [latex]p-\text{value}\leq\alpha[/latex], reject [latex]H_0[/latex] in favour of [latex]H_a[/latex].
- Write down a concluding sentence specific to the context of the question.
USING EXCEL TO CALCULE THE [latex]\color{white}{p-\text{value}}[/latex] FOR A HYPOTHESIS TEST ON A POPULATION PROPORTION
The [latex]p-\text{value}[/latex] for a hypothesis test on a population proportion is the area in the tail(s) of distribution of the sample proportion. If both [latex]n\times p\geq 5[/latex] and [latex]n\times(1-p)\geq 5[/latex], use the normal distribution to find the [latex]p-\text{value}[/latex]. If at least one of [latex]n\times p\lt 5[/latex] or [latex]n\times(1-p)\lt 5[/latex], use the binomial distribution to find the [latex]p-\text{value}[/latex].
If both [latex]n\times p\geq 5[/latex] and [latex]n\times(1-p)\geq 5[/latex]:
- The [latex]p-\text{value}[/latex] is the area in the tail(s) of a normal distribution, so use the norm.dist(x,[latex]\mu[/latex],[latex]\sigma[/latex],logic operator) function to calculate the [latex]p-\text{value}[/latex].
- For x, enter the value for [latex]\hat{p}[/latex].
- For [latex]\mu[/latex], enter the mean of the sample proportions [latex]p[/latex]. Note: Because the test is run assuming the null hypothesis is true, the value for [latex]p[/latex] is the claim from the null hypothesis.
- For [latex]\sigma[/latex], enter the standard error of the proportions [latex]\displaystyle{\sqrt{\frac{p\times(1-p)}{n}}}[/latex].
- For the logic operator, enter true. Note: Because we are calculating the area under the curve, we always enter true for the logic operator.
- Use the appropriate technique with the norm.dist function to find the area in the left-tail or the area in the right-tail.
If at least one of [latex]n\times p\lt 5[/latex] or [latex]n\times(1-p)\lt 5[/latex]:
- The [latex]p-\text{value}[/latex] is found using the binomial distribution.
- If the alternative hypothesis is a [latex]\lt[/latex], the [latex]p-\text{value}[/latex] is the probability of getting at most [latex]x[/latex] successes in [latex]n[/latex]trials where the probability of success is the claim about the population proportion [latex]p[/latex] in the null hypothesis.
- The [latex]p-\text{value}[/latex] is the output from the binom.dist(x,n,p,logic operator) function:
- For x, enter the number of successes.
- For n, enter the sample size.
- For p, enter the value of the population proportion [latex]p[/latex] from the null hypothesis.
- For the logic operator, enter true. Note: Because we are calculating an at most probability, the logic operator is always true.
- The [latex]p-\text{value}[/latex] is the output from the binom.dist(x,n,p,logic operator) function:
- If the alternative hypothesis is a [latex]\gt[/latex], the [latex]p-\text{value}[/latex] is the probability of getting at least [latex]x[/latex] successes in [latex]n[/latex] trials where the probability of success is the claim about the population proportion [latex]p[/latex] in the null hypothesis.
- The [latex]p-\text{value}[/latex] is the output from the 1-binom.dist(x-1,n,p,logic operator) function:
- For x, enter the number of successes.
- For n, enter the sample size.
- For p, enter the value of the population proportion [latex]p[/latex] in the null hypothesis.
- For the logic operator, enter true. Note: Because we are calculating an at least probability, the logic operator is always true.
- The [latex]p-\text{value}[/latex] is the output from the 1-binom.dist(x-1,n,p,logic operator) function:
EXAMPLE
Marketers believe that [latex]92\%[/latex] of adults own a cell phone. A cell phone manufacturer believes that number is actually lower. In a sample of [latex]200[/latex] adults, [latex]87\%[/latex] own a cell phone. At the [latex]1\%[/latex] significance level, determine if the proportion of adults that own a cell phone is lower than the marketers' claim.
Solution
Hypotheses:
[latex]\begin{eqnarray*}H_0:&&p=92\%\text{ of adults own a cell phone}\\H_a:&&p\lt 92\%\text{ of adults own a cell phone}\end{eqnarray*}[/latex]
[latex]p-\text{value}[/latex]:
From the question, we have [latex]n=200[/latex], [latex]\hat{p}=0.87[/latex], and [latex]\alpha=0.01[/latex].
To determine the distribution, we check [latex]n\times p[/latex] and [latex]n\times(1-p)[/latex]. For the value of [latex]p[/latex], we use the claim from the null hypothesis ([latex]p=0.92[/latex]).
[latex]\begin{eqnarray*}n\times p&=&200\times 0.92=184\geq 5\\n\times(1-p)&=&200\times(1-0.92)=16\geq 5\end{eqnarray*}[/latex]
Because both [latex]n \times p \geq 5[/latex] and [latex]n\times(1-p)\geq 5[/latex], we use a normal distribution to calculate the [latex]p-\text{value}[/latex]. Because the alternative hypothesis is a [latex]\lt[/latex], the [latex]p-\text{value}[/latex] is the area in the left tail of the distribution.
| Function | norm.dist |
|---|---|
| Field 1 | 0.87 |
| Field 2 | 0.92 |
| Field 3 | sqrt(0.92*(1-0.92)/200) |
| Field 4 | true |
| Answer | 0.0046 |
So the [latex]p-\text{value}=0.0046[/latex].
Conclusion:
Because [latex]p-\text{value}=0.0046\lt 0.01=\alpha[/latex], we reject the null hypothesis in favour of the alternative hypothesis. At the [latex]1\%[/latex] significance level there is enough evidence to suggest that the proportion of adults who own a cell phone is lower than [latex]92\%[/latex].
NOTES
- The null hypothesis [latex]p=92\%[/latex] is the claim that [latex]92\%[/latex] of adults own a cell phone.
- The alternative hypothesis [latex]p\lt 92\%[/latex] is the claim that less than [latex]92\%[/latex] of adults own a cell phone.
- The [latex]p-\text{value}[/latex] is the area in the left tail of the sampling distribution, to the left of [latex]\hat{p}=0.87[/latex]. In the calculation of the [latex]p-\text{value}[/latex]:
- The function is norm.dist because we are finding the area in the left tail of a normal distribution.
- Field 1 is the value of [latex]\hat{p}[/latex].
- Field 2 is the value of [latex]p[/latex] from the null hypothesis. Remember, we run the test assuming the null hypothesis is true, so that means we assume [latex]p=0.92[/latex].
- Field 3 is the standard deviation for the sample proportions [latex]\displaystyle{\sqrt{\frac{p\times(1-p)}{n}}}[/latex].
- The [latex]p-\text{value}[/latex] of [latex]0.0046[/latex] tells us that under the assumption that [latex]92\%[/latex] of adults own a cell phone (the null hypothesis), there is only a [latex]0.46\%[/latex] chance that the proportion of adults who own a cell phone in a sample of [latex]200[/latex] is [latex]87\%[/latex] or less. This is a small probability, and so is unlikely to happen, assuming the null hypothesis is true. This suggests that the assumption that the null hypothesis is true is most likely incorrect, and so the conclusion of the test is to reject the null hypothesis in favour of the alternative hypothesis. In other words, the proportion of adults who own a cell phone is most likely less than [latex]92\%[/latex].
EXAMPLE
A consumer group claims that the proportion of households that have at least three cell phones is [latex]30\%[/latex]. A cell phone company has reason to believe that the proportion of households with at least three cell phones is much higher. Before they start a big advertising campaign based on the proportion of households that have at least three cell phones, they want to test their claim. Their marketing people survey [latex]150[/latex] households with the result that [latex]54[/latex] of the households have at least three cell phones. At the [latex]1\%[/latex] significance level, determine if the proportion of households that have at least three cell phones is more than [latex]30\%[/latex].
Solution
Hypotheses:
[latex]\begin{eqnarray*}H_0:&&p=30\%\text{ of household have at least 3 cell phones}\\H_a:&&p\gt 30\%\text{ of household have at least 3 cell phones}\end{eqnarray*}[/latex]
[latex]p-\text{value}[/latex]:
From the question, we have [latex]n=150[/latex], [latex]\displaystyle{\hat{p}=\frac{54}{150}=0.36}[/latex], and [latex]\alpha=0.01[/latex].
To determine the distribution, we check [latex]n\times p[/latex] and [latex]n\times(1-p)[/latex]. For the value of [latex]p[/latex], we use the claim from the null hypothesis ([latex]p=0.3[/latex]).
[latex]\begin{eqnarray*}n\times p&=&150\times 0.3=45\geq 5\\n\times(1-p)&=&150\times(1-0.3)=105\geq 5\end{eqnarray*}[/latex]
Because both [latex]n \times p \geq 5[/latex] and [latex]n\times(1-p)\geq5[/latex], we use a normal distribution to calculate the [latex]p-\text{value}[/latex]. Because the alternative hypothesis is a [latex]\gt[/latex], the [latex]p-\text{value}[/latex] is the area in the right tail of the distribution.
| Function | 1-norm.dist |
|---|---|
| Field 1 | 0.36 |
| Field 2 | 0.3 |
| Field 3 | sqrt(0.3*(1-0.3)/150) |
| Field 4 | true |
| Answer | 0.0544 |
So the [latex]p-\text{value}=0.0544[/latex].
Conclusion:
Because [latex]p-\text{value}=0.0544\gt 0.01=\alpha[/latex], we do not reject the null hypothesis. At the [latex]1\%[/latex] significance level, there is not enough evidence to suggest that the proportion of households with at least three cell phones is more than [latex]30\%[/latex].
NOTES
- The null hypothesis [latex]p=30\%[/latex] is the claim that [latex]30\%[/latex] of households have at least three cell phones.
- The alternative hypothesis [latex]p\gt 30\%[/latex] is the claim that more than [latex]30\%[/latex] of households have at least three cell phones.
- The [latex]p-\text{value}[/latex] is the area in the right tail of the sampling distribution, to the right of [latex]\hat{p}=0.36[/latex]. In the calculation of the [latex]p-\text{value}[/latex]:
- The function is 1-norm.dist because we are finding the area in the right tail of a normal distribution.
- Field 1 is the value of [latex]\hat{p}[/latex].
- Field 2 is the value of [latex]p[/latex] from the null hypothesis. Remember, we run the test assuming the null hypothesis is true, so that means we assume [latex]p=0.3[/latex].
- Field 3 is the standard deviation for the sample proportions [latex]\displaystyle{\sqrt{\frac{p\times(1-p)}{n}}}[/latex].
- The [latex]p-\text{value}[/latex] of 0.0544 tells us that under the assumption that [latex]30\%[/latex] of households have at least three cell phones (the null hypothesis), there is a [latex]5.44\%[/latex] chance that the proportion of households with at least three cell phones in a sample of [latex]150[/latex] is [latex]36\%[/latex] or more. Compared to the [latex]1\%[/latex] significance level, this is a large probability, and so is likely to happen, assuming the null hypothesis is true. This suggests that the assumption that the null hypothesis is true is most likely correct, and so the conclusion of the test is to not reject the null hypothesis. In other words, the claim that [latex]30\%[/latex] of households have at least three cell phones is most likely correct.
TRY IT
A teacher believes that [latex]70\%[/latex] of students in the class will want to go on a field trip to the local zoo. The students in the class believe the proportion is much higher and ask the teacher to verify her claim. The teacher samples [latex]50[/latex] students, and [latex]39[/latex] reply that they would want to go to the zoo. At the [latex]5\%[/latex] significance level, determine if the proportion of students who want to go on the field trip is higher than [latex]70\%[/latex].
Click to see Solution
Hypotheses:
[latex]\begin{eqnarray*}H_0:&&p=70\%\text{ of students want to go on the field trip}\\H_a:&&p\gt 70\%\text{ of students want to go on the field trip}\end{eqnarray*}[/latex]
[latex]p-\text{value}[/latex]:
From the question, we have [latex]n=50[/latex], [latex]\displaystyle{\hat{p}=\frac{39}{50}=0.78}[/latex], and [latex]\alpha=0.05[/latex].
[latex]\begin{eqnarray*}n\times p&=&50\times 0.7=35\geq 5\\n\times(1-p)&=&50\times(1-0.7)=15\geq 5\end{eqnarray*}[/latex]
Because both [latex]n \times p \geq 5[/latex] and [latex]n\times(1-p)\geq 5[/latex] we use a normal distribution to calculate the [latex]p-\text{value}[/latex]. Because the alternative hypothesis is a [latex]\gt[/latex], the [latex]p-\text{value}[/latex] is the area in the right tail of the distribution.
| Function | 1-norm.dist |
|---|---|
| Field 1 | 0.78 |
| Field 2 | 0.7 |
| Field 3 | sqrt(0.7*(1-0.7)/50) |
| Field 4 | true |
| Answer | 0.1085 |
So the [latex]p-\text{value}=0.1085[/latex].
Conclusion:
Because [latex]p-\text{value}=0.1085\gt 0.05=\alpha[/latex], we do not reject the null hypothesis. At the [latex]5\%[/latex] significance level, there is not enough evidence to suggest that the proportion of students who want to go on the field trip is higher than [latex]70\%[/latex].
NOTES
- The null hypothesis [latex]p=70\%[/latex] is the claim that [latex]70\%[/latex] of the students want to go on the field trip.
- The alternative hypothesis [latex]p\gt 70\%[/latex] is the claim that more than [latex]70\%[/latex] of students want to go on the field trip.
- The [latex]p-\text{value}[/latex] of [latex]0.1085[/latex] tells us that under the assumption that [latex]70\%[/latex] of students want to go on the field trip (the null hypothesis), there is a [latex]10.85\%[/latex] chance that the proportion of students who want to go on the field trip in a sample of [latex]50[/latex] students is [latex]78\%[/latex] or more. Compared to the [latex]5\%[/latex] significance level, this is a large probability, and so is likely to happen, assuming the null hypothesis is true. This suggests that the assumption that the null hypothesis is true is most likely correct, and so the conclusion of the test is to not reject the null hypothesis. In other words, the teacher's claim that [latex]70\%[/latex] of students want to go on the field trip is most likely correct.
EXAMPLE
Joan believes that [latex]50\%[/latex] of first-time brides in the United States are younger than their grooms. She performs a hypothesis test to determine if the percentage is the same or different from [latex]50\%[/latex]. Joan samples [latex]100[/latex] first-time brides and [latex]56[/latex] reply that they are younger than their grooms. Use a [latex]5\%[/latex] significance level.
Solution
Hypotheses:
[latex]\begin{eqnarray*}H_0:&&p=50\%\text{ of first-time brides are younger than the groom}\\H_a:&&p\neq 50\%\text{ of first-time brides are younger than the groom}\end{eqnarray*}[/latex]
[latex]p-\text{value}[/latex]:
From the question, we have [latex]n=100[/latex], [latex]\displaystyle{\hat{p}=\frac{56}{100}=0.56}[/latex], and [latex]\alpha=0.05[/latex].
To determine the distribution, we check [latex]n\times p[/latex] and [latex]n\times(1-p)[/latex]. For the value of [latex]p[/latex], we use the claim from the null hypothesis ([latex]p=0.5[/latex]).
[latex]\begin{eqnarray*}n\times p&=&100\times 0.5=50\geq 5\\n\times(1-p)&=&100\times(1-0.5)=50\geq 5\end{eqnarray*}[/latex]
Because both [latex]n \times p \geq 5[/latex] and [latex]n\times(1-p)\geq 5[/latex], we use a normal distribution to calculate the [latex]p-\text{value}[/latex]. Because the alternative hypothesis is a [latex]\neq[/latex], the [latex]p-\text{value}[/latex] is the sum of the area in the tails of the distribution.
Because there is only one sample, we only have information relating to one of the two tails, either the left or the right. We need to know if the sample relates to the left or right tail because that will determine how we calculate out the area of that tail using the normal distribution. In this case, the sample proportion [latex]\hat{p}=0.56[/latex] is greater than the value of the population proportion in the null hypothesis [latex]p=0.5[/latex] ([latex]\hat{p}=0.56>0.5=p[/latex]), so the sample information relates to the right-tail of the normal distribution. This means that we will calculate out the area in the right tail using 1-norm.dist. However, this is a two-tailed test where the [latex]p-\text{value}[/latex] is the sum of the area in the two tails, and the area in the right-tail is only one half of the [latex]p-\text{value}[/latex]. The area in the left tail equals the area in the right tail, and the [latex]p-\text{value}[/latex] is the sum of these two areas.
| Function | 1-norm.dist |
|---|---|
| Field 1 | 0.56 |
| Field 2 | 0.5 |
| Field 3 | sqrt(0.5*(1-0.5)/100) |
| Field 4 | true |
| Answer | 0.1151 |
So the area in the right tail is [latex]0.1151[/latex] and [latex]\frac{1}{2}p-\text{value}=0.1151[/latex]. This is also the area in the left tail, so
[latex]p-\text{value}=0.1151+0.1151=0.2302[/latex]
Conclusion:
Because [latex]p-\text{value}=0.2302\gt 0.05=\alpha[/latex], we do not reject the null hypothesis. At the [latex]5\%[/latex] significance level, there is not enough evidence to suggest that the proportion of first-time brides that are younger than the groom is different from [latex]50\%[/latex].
NOTES
- The null hypothesis [latex]p=50\%[/latex] is the claim that the proportion of first-time brides that are younger than the groom is [latex]50\%[/latex].
- The alternative hypothesis [latex]p\neq 50\%[/latex] is the claim that the proportion of first-time brides that are younger than the groom is different from [latex]50\%[/latex].
- In a two-tailed hypothesis test that uses the normal distribution, we will only have sample information relating to one of the two tails. We must determine which of the tails the sample information belongs to, and then calculate out the area in that tail. The area in each tail represents exactly half of the [latex]p-\text{value}[/latex], so the [latex]p-\text{value}[/latex] is the sum of the areas in the two tails.
- If the sample proportion [latex]\hat{p}[/latex] is less than the population proportion [latex]p[/latex] in the null hypothesis ([latex]\hat{p}\lt p[/latex]), the sample information belongs to the left tail.
- We use norm.dist([latex]\hat{p}[/latex],[latex]p[/latex],[latex]\text{sqrt}(p*(1-p)/n)[/latex],true) to find the area in the left tail. The area in the right tail equals the area in the left tail, so we can find the [latex]p-\text{value}[/latex] by adding the output from this function to itself.
- If the sample proportion [latex]\hat{p}[/latex] is greater than the population proportion [latex]p[/latex] in the null hypothesis ([latex]\hat{p}\gt p[/latex]), the sample information belongs to the right tail.
- We use 1-norm.dist([latex]\hat{p}[/latex],[latex]p[/latex],[latex]\text{sqrt}(p*(1-p)/n)[/latex],true) to find the area in the right tail. The area in the left tail equals the area in the right tail, so we can find the [latex]p-\text{value}[/latex] by adding the output from this function to itself.
- If the sample proportion [latex]\hat{p}[/latex] is less than the population proportion [latex]p[/latex] in the null hypothesis ([latex]\hat{p}\lt p[/latex]), the sample information belongs to the left tail.
- The [latex]p-\text{value}[/latex] of [latex]0.2302[/latex] is a large probability compared to the [latex]5\%[/latex] significance level, and so is likely to happen assuming the null hypothesis is true. This suggests that the assumption that the null hypothesis is true is most likely correct, and so the conclusion of the test is to not reject the null hypothesis. In other words, the claim that the proportion of first-time brides who are younger than the groom is most likely correct.
Video: "Excel Statistical Analysis 49: Hypothesis Testing for Proportion (Binominal) using Normal Curve" by excelisfun [7:27] is licensed under the Standard YouTube License.Transcript and closed captions available on YouTube.
EXAMPLE
An online retailer believes that [latex]93\%[/latex] of the visitors to its website will make a purchase. A researcher in the marketing department thinks the actual percentage is lower than claimed. The researcher examines a sample of [latex]50[/latex] visits to the website and finds that [latex]45[/latex] of the visits resulted in a purchase. At the [latex]1\%[/latex] significance level, determine if the proportion of visits to the website that result in a purchase is lower than claimed.
Solution
Hypotheses:
[latex]\begin{eqnarray*}H_0:&&p=93\%\text{ of visitors make a purchase}\\H_a:&&p\lt 93\%\text{ of visitors make a purchase}\end{eqnarray*}[/latex]
[latex]p-\text{value}[/latex]:
From the question, we have [latex]n=50[/latex], [latex]x=45[/latex], and [latex]\alpha=0.01[/latex].
To determine the distribution, we check [latex]n\times p[/latex] and [latex]n\times(1-p)[/latex]. For the value of [latex]p[/latex], we use the claim from the null hypothesis ([latex]p=0.93[/latex]).
[latex]\begin{eqnarray*}n\times p&=&50\times 0.93=46.5\geq 5\\n\times(1-p)&=&50\times(1-0.93)=3.5\lt 5\end{eqnarray*}[/latex]
Because [latex]n \times (1-p) \lt 5[/latex], we use a binomial distribution to calculate the [latex]p-\text{value}[/latex]. Because the alternative hypothesis is a [latex]\lt[/latex], the [latex]p-\text{value}[/latex] is the probability of getting at most [latex]45[/latex] successes in [latex]50[/latex] trials.
| Function | binom.dist |
|---|---|
| Field 1 | 45 |
| Field 2 | 50 |
| Field 3 | 0.93 |
| Field 4 | true |
| Answer | 0.2710 |
So the [latex]p-\text{value}=0.2710[/latex].
Conclusion:
Because [latex]p-\text{value}=0.2710\gt 0.01=\alpha[/latex], we do not reject the null hypothesis. At the [latex]1\%[/latex] significance level there is not enough evidence to suggest that the proportion of visitors who make a purchase is lower than [latex]93\%[/latex].
NOTES
- The null hypothesis [latex]p=93\%[/latex] is the claim that [latex]93\%[/latex] of visitors to the website make a purchase.
- The alternative hypothesis [latex]p\lt 93\%[/latex] is the claim that less than [latex]93\%[/latex] of visitors to the website make a purchase.
- The [latex]p-\text{value}[/latex] is the binomial probability of getting at most [latex]45[/latex] successes (the number in the sample with the characteristic of interest) in [latex]50[/latex] trials (the sample size) with a probability of success of [latex]93\%[/latex] (the value of [latex]p[/latex] in the null hypothesis). In the calculation of the [latex]p-\text{value}[/latex]:
- The function is binom.dist because we are finding the probability of at most [latex]45[/latex] successes.
- Field 1 is the number of successes [latex]x[/latex].
- Field 2 is the sample size [latex]n[/latex].
- Field 3 is the probability of success [latex]p[/latex]. This is the claim about the population proportion made in the null hypothesis, so that means we assume [latex]p=0.93[/latex].
- The [latex]p-\text{value}[/latex] of [latex]0.2710[/latex] tells us that under the assumption that [latex]93\%[/latex] of visitors make a purchase (the null hypothesis), there is a [latex]27.10\%[/latex] chance that the number of visitors in a sample of [latex]50[/latex] who make a purchase is [latex]45[/latex] or less. This is a large probability compared to the significance level, and so is likely to happen assuming the null hypothesis is true. This suggests that the assumption that the null hypothesis is true is most likely correct, and so the conclusion of the test is to not reject the null hypothesis. In other words, the proportion of visitors to the website who make a purchase, adults is most likely [latex]93\%[/latex].
EXAMPLE
A drug company claims that only [latex]4\%[/latex] of people who take their new drug experience any side effects from the drug. A researcher believes that the percentage is higher than the drug company's claim. The researcher takes a sample of [latex]80[/latex] people who take the drug and finds that [latex]10\%[/latex] of the people in the sample experience side effects from the drug. At the [latex]5\%[/latex] significance level, determine if the proportion of people who experience side effects from taking the drug is higher than claimed.
Solution
Hypotheses:
[latex]\begin{eqnarray*}H_0:&&p=4\%\text{ of people experience side effects}\\H_a:&&p\gt 4\%\text{ of people experience side effects}\end{eqnarray*}[/latex]
[latex]p-\text{value}[/latex]:
From the question, we have [latex]n=80[/latex], [latex]\hat{p}=0.1[/latex], and [latex]\alpha=0.05[/latex].
To determine the distribution, we check [latex]n\times p[/latex] and [latex]n\times(1-p)[/latex]. For the value of [latex]p[/latex], we use the claim from the null hypothesis ([latex]p=0.04[/latex]).
[latex]\begin{eqnarray*}n\times p&=&80\times 0.04=3.2\lt 5\end{eqnarray*}[/latex]
Because [latex]n\times p\lt 5[/latex], we use a binomial distribution to calculate the [latex]p-\text{value}[/latex]. Because the alternative hypothesis is a [latex]\gt[/latex], the [latex]p-\text{value}[/latex] is the probability of getting at least [latex]8[/latex] successes in [latex]80[/latex] trials. (Note: In the sample of size [latex]80[/latex], [latex]10\%[/latex] have the characteristic of interest, so this means that [latex]80\times 0.1=8[/latex] people in the sample have the characteristic of interest.)
| Function | 1-binom.dist |
|---|---|
| Field 1 | 7 |
| Field 2 | 80 |
| Field 3 | 0.04 |
| Field 4 | true |
| Answer | 0.0147 |
So the [latex]p-\text{value}=0.0147[/latex].
Conclusion:
Because [latex]p-\text{value}=0.0147\lt 0.05=\alpha[/latex], we reject the null hypothesis in favour of the alternative hypothesis. At the [latex]5\%[/latex] significance level, there is enough evidence to suggest that the proportion of people who experience side effects from taking the drug is higher than [latex]4\%[/latex].
NOTES
- The null hypothesis [latex]p=4\%[/latex] is the claim that [latex]4\%[/latex] of the people experience side effects from taking the drug.
- The alternative hypothesis [latex]p\gt 4\%[/latex] is the claim that more than [latex]4\%[/latex] of the people experience side effects from taking the drug.
- The [latex]p-\text{value}[/latex] is the binomial probability of getting at least [latex]8[/latex] successes (the number in the sample with the characteristic of interest) in [latex]80[/latex] trials (the sample size) with a probability of success of [latex]4\%[/latex] (the value of [latex]p[/latex] in the null hypothesis). In the calculation of the [latex]p-\text{value}[/latex]:
- The function is 1-binom.dist because we are finding the probability of at least [latex]8[/latex] successes.
- Field 1 is [latex]x-1[/latex] where [latex]x[/latex] is the number of successes. In this case, we are using the compliment rule to change the probability of at least [latex]8[/latex] successes into [latex]1[/latex] minus the probability of at most [latex]7[/latex] successes.
- Field 2 is the sample size [latex]n[/latex].
- Field 3 is the probability of success [latex]p[/latex]. This is the claim about the population proportion made in the null hypothesis, so that means we assume [latex]p=0.04[/latex].
- The [latex]p-\text{value}[/latex] of [latex]0.0147[/latex] tells us that under the assumption that [latex]4\%[/latex] of people experience side effects (the null hypothesis), there is a [latex]1.47\%[/latex] chance that the number of people in a sample of [latex]80[/latex] who experience side effects is [latex]8[/latex] or more. This is a small probability compared to the significance level, and so is unlikely to happen, assuming the null hypothesis is true. This suggests that the assumption that the null hypothesis is true is most likely incorrect, and so the conclusion of the test is to reject the null hypothesis in favour of the alternative hypothesis. In other words, the proportion of people who experience side effects is most likely greater than [latex]4\%[/latex].
Exercises
- Your statistics instructor claims that [latex]60\%[/latex] of the students who take her Elementary Statistics class go through life feeling more enriched. For some reason that she cannot quite figure out, most people do not believe her. You decide to check this out on your own. You randomly survey [latex]64[/latex] of her past Elementary Statistics students and find that [latex]34[/latex] feel more enriched as a result of her class. At the [latex]5\%[/latex] significance level. test if the percentage of students who feel enriched after taking the statistics class is less than the instructor's claim.
Click to see Answer
- Hypotheses: [latex]\begin{eqnarray*}H_0:&&p=60\%\text{ of students feel more enriched}\\H_a:&&p\lt 60\%\text{ of students feel more enriched}\end{eqnarray*}[/latex]
- [latex]p-\text{value}=0.1308[/latex]
- Conclusion: At the [latex]5\%[/latex] significance level, there is not enough evidence to conclude that the percentage of students who feel enriched after taking the statistics class is less than [latex]60\%[/latex].
- Toastmasters International cites a report by Gallop Poll that [latex]40\%[/latex] of people fear public speaking. A student believes that less than [latex]40\%[/latex] of students at her school fear public speaking. She randomly surveys [latex]361[/latex] schoolmates and finds that [latex]135[/latex] report they fear public speaking. At the [latex]1\%[/latex] significance level, test to determine if the percentage of students at the school who fear public speaking is less than [latex]40\%[/latex].
Click to see Answer
- Hypotheses: [latex]\begin{eqnarray*}H_0:&&p=40\%\text{ of students fear public speaking}\\H_a:&&p\lt 40\%\text{ of students fear public speaking}\end{eqnarray*}[/latex]
- [latex]p-\text{value}=0.1563[/latex]
- Conclusion: At the [latex]1\%[/latex] significance level, there is not enough evidence to conclude that the percentage of students who fear public speaking is less than [latex]40\%[/latex].
- According to an article in Bloomberg Businessweek, New York City's most recent adult smoking rate is [latex]14\%[/latex]. Suppose that a survey is conducted to determine this year’s rate. In a sample of [latex]70[/latex] randomly chosen New York City residents, [latex]16[/latex] replied that they smoke. At the [latex]5\%[/latex] significance level, determine if the smoking rate in New York City has changed.
Click to see Answer
- Hypotheses: [latex]\begin{eqnarray*}H_0:&&p=14\%\text{ of New York City residents smoke}\\H_a:&&p\neq 14\%\text{ of New York City residents smoke}\end{eqnarray*}[/latex]
- [latex]p-\text{value}=0.0327[/latex]
- Conclusion: At the [latex]5\%[/latex] significance level, there is enough evidence to conclude that the smoking rate in New York City has changed.
- According to the Center for Disease Control website, in 2011, [latex]18\%[/latex] of high school students have smoked a cigarette. A statistics class at a local high school wants to determine if the proportion of students who have smoked a cigarette at their high school is higher than this claim. In a sample of [latex]150[/latex] students, [latex]24\%[/latex] said they have smoked a cigarette. At the [latex]5\%[/latex] significance level, test the statistics class's claim.
Click to see Answer
- Hypotheses: [latex]\begin{eqnarray*}H_0:&&p=18\%\text{ of students have smoked}\\H_a:&&p\gt 18\%\text{ of students have smoked}\end{eqnarray*}[/latex]
- [latex]p-\text{value}=0.0279[/latex]
- Conclusion: At the [latex]5\%[/latex] significance level, there is enough evidence to conclude that the proportion of students at the high school who have smoked a cigarette is greater than [latex]18\%[/latex].
- A recent survey in the N.Y. Times Almanac indicated that [latex]48.8\%[/latex] of families own stock. A broker wanted to determine if this survey is valid. He surveyed a random sample of [latex]250[/latex] families and found that [latex]142[/latex] owned some type of stock. At the [latex]1\%[/latex] significance level, determine if the proportion of families who own stock is different than the result claimed by the survey.
Click to see Answer
- Hypotheses: [latex]\begin{eqnarray*}H_0:&&p=48.8\%\text{ of families own stock}\\H_a:&&p\neq 48.8\%\text{ of families own stock}\end{eqnarray*}[/latex]
- [latex]p-\text{value}=0.0114[/latex]
- Conclusion: At the [latex]1\%[/latex] significance level, there is not enough evidence to conclude that the proportion of families who own stock is different than [latex]48.8\%[/latex].
- According to a national driving association, driver error is listed as the cause of approximately [latex]54\%[/latex] of all fatal automobile accidents. A local insurance agent doubts this claim, suspecting the actual percentage is higher. The insurance agent takes a sample of [latex]60[/latex] fatal automobile accidents and finds that [latex]65\%[/latex] were caused by driver error. At the [latex]5\%[/latex] significance level, determine if the percentage of automobile accidents caused by driver error is higher than claimed.
Click to see Answer
- Hypotheses: [latex]\begin{eqnarray*}H_0:&&p=54\%\text{ of automobile accidents caused by driver error}\\H_a:&&p\gt 54\%\text{ of automobile accidents caused by driver error}\end{eqnarray*}[/latex]
- [latex]p-\text{value}=0.0437[/latex]
- Conclusion: At the [latex]5\%[/latex] significance level, there is enough evidence to conclude that the percentage of automobile accidents caused by driver error is greater than [latex]54\%[/latex].
- According to a library association, [latex]67\%[/latex] of patrons borrow books. The director of a local library believes that the proportion of patrons who borrow books at her library is different from this claim. In a sample of [latex]100[/latex] patrons of the local library, [latex]57[/latex] borrowed books. At the [latex]1\%[/latex] significance level, is the proportion of patrons who borrow books at the local library different from the library association's claim?
Click to see Answer
- Hypotheses: [latex]\begin{eqnarray*}H_0:&&p=67\%\text{ of patrons borrow books}\\H_a:&&p\neq 67\%\text{ of patrons borrow books}\end{eqnarray*}[/latex]
- [latex]p-\text{value}=0.0334[/latex]
- Conclusion: At the [latex]1\%[/latex] significance level, there is not enough evidence to conclude that the proportion of patrons who borrow books at the local library is different than [latex]67\%[/latex].
- An all-inclusive resort claims that their guest satisfaction rating is [latex]97\%[/latex]. In a sample of [latex]80[/latex] guests at the resort, [latex]74[/latex] said they were satisfied with their stay. At the [latex]5\%[/latex] significance level, determine if the satisfaction rate of guests at the resort is less than claimed.
Click to see Answer
- Hypotheses: [latex]\begin{eqnarray*}H_0:&&p=97\%\text{ satisfaction rating}\\H_a:&&p\lt 97\%\text{ satisfaction rating}\end{eqnarray*}[/latex]
- [latex]p-\text{value}=0.0333[/latex]
- Conclusion: At the [latex]5\%[/latex] significance level, there is enough evidence to conclude that the satisfaction rating of guests at the resort is less than claimed.
- A drug company claims that only [latex]9\%[/latex] of people who take their new drug experience any side effects. A researcher wants to test this claim. In a sample of [latex]45[/latex] people taking the drug, [latex]9[/latex] reported side effects. At the [latex]5\%[/latex] significance level, determine if the proportion of people on the drug who experience side effects is more than claimed.
Click to see Answer
- Hypotheses: [latex]\begin{eqnarray*}H_0:&&p=9\%\text{ of people on the drug experience side effects}\\H_a:&&p\gt 9\%\text{ of people on the drug experience side effects}\end{eqnarray*}[/latex]
- [latex]p-\text{value}=0.0174[/latex]
- Conclusion: At the [latex]5\%[/latex] significance level, there is enough evidence to conclude that the proportion of people on the drug who experience side effects is more than [latex]9\%[/latex].
- A company that produces a product to help people stop smoking claims that [latex]95\%[/latex] of smokers who use the product stop smoking within six months. In a study to test this claim, [latex]30[/latex] smokers use the product for six months. At the end of the six months, [latex]25[/latex] of the smokers in the study claim they have stopped smoking. At the [latex]1\%[/latex] significance level, test if the proportion of smokers who use the product stop smoking after six months is less than claimed.
Click to see Answer
- Hypotheses: [latex]\begin{eqnarray*}H_0:&&p=95\%\text{ of smokers stop smoking}\\H_a:&&p\lt 95\%\text{ of smokers stop smoking}\end{eqnarray*}[/latex]
- [latex]p-\text{value}=0.0156[/latex]
- Conclusion: At the [latex]1\%[/latex] significance level, there is not enough evidence to conclude that the proportion of smokers who use the product stop smoking after six months is less than [latex]95\%[/latex].
- A more-than-ten-year-old study reported that [latex]10\%[/latex] of consumers purchased something from an online retailer at least once a week. With the increase in e-commerce and online shopping, a researcher on consumer behaviour believes this percentage is higher today. The researcher takes a sample of [latex]40[/latex] consumers, and finds that [latex]22.5\%[/latex] of them purchase something from an online retailer at least once a week. At the [latex]5\%[/latex] significance level, determine the percentage of consumers who purchase something from an online retailer at least once a week is higher than the claim made in the old study.
Click to see Answer
- Hypotheses: [latex]\begin{eqnarray*}H_0:&&p=10\%\text{ of consumers shop online at least once a week}\\H_a:&&p\gt 10\%\text{ of consumers shop online at least once a week}\end{eqnarray*}[/latex]
- [latex]p-\text{value}=0.0155[/latex]
- Conclusion: At the [latex]5\%[/latex] significance level, there is enough evidence to conclude that the percentage of consumers who purchase something online at least once a week is more than [latex]10\%[/latex].
"8.8 Hypothesis Tests for a Population Proportion" and “8.9 Exercises” from Introduction to Statistics by Valerie Watts is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.