7.5 Calculating the Sample Size for a Confidence Interval
LEARNING OBJECTIVES
- Calculate the minimum sample size required to estimate a population parameter.
Usually, we have no control over the sample size of a data set. However, if we are able to set the sample size, as in cases where we are taking a survey, it is very helpful to know just how large the sample should be to provide the most information. Sampling can be very costly, in time, product, and money. For example, simple telephone surveys will cost approximately [latex]\$30.00[/latex] each, and some sampling requires the destruction of the product. Selecting a sample that is too large is expensive and time-consuming. But selecting a sample that is too small can lead to inaccurate conclusions. We want to find the minimum sample size required to achieve the desired level of accuracy in a confidence interval.
Calculating the Sample Size for a Population Mean
The margin of error [latex]E[/latex] for a confidence interval for a population mean is
[latex]\displaystyle{E=\frac{z \times \sigma}{\sqrt{n}}}[/latex]
where [latex]z[/latex] is the [latex]z[/latex]-score so that the area under the standard normal distribution in between [latex]-z[/latex] and [latex]z[/latex] is the confidence level [latex]C[/latex].
Rearranging this formula, we get a formula for the sample size [latex]n[/latex]:
[latex]\displaystyle{n=\left(\frac{z \times \sigma}{E}\right)^2}[/latex]
In order to use this formula, we need values for [latex]z[/latex], [latex]E[/latex] and [latex]\sigma[/latex]:
- The value for [latex]z[/latex] is determined by the confidence level of the confidence interval, calculated the same way we calculate the [latex]z[/latex]-score for a confidence interval.
- The value for the margin of error [latex]E[/latex] is set as the predetermined acceptable error, or tolerance, for the difference between the sample mean [latex]\overline{x}[/latex] and the population mean [latex]\mu[/latex]. In other words, [latex]E[/latex] is set to the maximum allowable width of the confidence interval.
- An estimate for the population standard deviation [latex]\sigma[/latex] can be found by one of the following methods:
- Conduct a small pilot study and use the sample standard deviation from the pilot study as an estimate for [latex]\sigma[/latex].
- Use the sample standard deviation from previously collected data as an estimate for [latex]\sigma[/latex]. Although crude, this method of estimating the standard deviation may help reduce costs significantly.
- Use [latex]\displaystyle{\frac{\text{Range}}{4}}[/latex] as an estimate for [latex]\sigma[/latex], where [latex]\text{Range}[/latex] is the difference between the maximum and minimum values of the population under study.
NOTES
- Although we do not know the population standard deviation when calculating the sample size, we do not use the [latex]t[/latex]-distribution in the sample size formula. In order to use the [latex]t[/latex]-distribution in this situation, we need the degrees of freedom [latex]n-1[/latex]. But [latex]n[/latex] is the sample size we are trying to estimate. So, we must use the normal distribution to determine the sample size.
- The value of [latex]n[/latex] determined from the formula is the minimum sample size required to achieve the desired level of confidence. The sample size [latex]n[/latex] is a count, and so is an integer. It would be unusual for the value of [latex]n[/latex] generated by the formula to be an integer. Because [latex]n[/latex] is the minimum sample size required, we must round the output from the formula up to the next integer. If we round the value of [latex]n[/latex] down, the sample size will be below the minimum required sample size.
- After we find the sample size [latex]n[/latex] and collected the data for the sample, we use the appropriate confidence interval formula and the sample standard deviation from the actual sample (assuming [latex]\sigma[/latex] is unknown), and not the estimate of the standard deviation used in the calculation of the sample size.
CALCULATING THE [latex]\color{white}{z}[/latex]-SCORE FOR SAMPLE SIZE IN EXCEL
To find the [latex]z[/latex]-score to calculate the sample size for a confidence interval with confidence level [latex]C[/latex], use the norm.s.inv(area to the left of z) function.
- For area to the left of z, enter the entire area to the left of the [latex]z[/latex]-score required. For a confidence interval, the area to the left of [latex]z[/latex] is [latex]\displaystyle{C+\frac{1-C}{2}}[/latex].
The output from the norm.s.inv function is the value of [latex]z[/latex]-score needed to find the sample size.
NOTE
The norm.s.inv function requires that we enter the entire area to the left of the unknown [latex]z[/latex]-score. This area includes the confidence level [latex]C[/latex] (the area in the middle of the distribution) plus the remaining area in the left tail [latex]\frac{1-C}{2}[/latex].
EXAMPLE
We want to estimate the mean age of Foothill College students. From previous information, an estimate of the standard deviation of the ages of the students is [latex]15[/latex] years. We want to be [latex]95\%[/latex] confident that the sample mean age is within two years of the population mean age. How many randomly selected Foothill College students must be surveyed to achieve the desired level of accuracy?
Solution
To find the sample size, we need to find the [latex]z[/latex]-score for the [latex]95\%[/latex] confidence interval. This means that we need to find the [latex]z[/latex]-score from the standard normal distribution so that the entire area to the left of [latex]z[/latex] is [latex]\displaystyle{0.95+\frac{1-0.95}{2}=0.975}[/latex].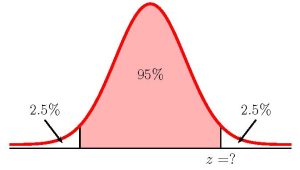
| Function | norm.s.inv |
|---|---|
| Field 1 | 0.975 |
| Answer | 1.9599… |
So [latex]z=1.9599....[/latex]. From the question [latex]\sigma \simeq 15[/latex] and [latex]E=2[/latex].
[latex]\begin{eqnarray*}n & = & \left(\frac{z \times \sigma}{E}\right)^2 \\ & = & \left( \frac{1.9599... \times 15}{2}\right)^2 \\ & = & 216.08... \\ & \Rightarrow & 217 \text{ students}\end{eqnarray*}[/latex]
[latex]217[/latex] students must be surveyed to achieve the desired accuracy.
NOTE
Remember to round the value for the sample size UP to the next integer. This ensures that the sample size is an integer and is large enough. Do not forget to include appropriate units with the sample size.
TRY IT
You want to estimate the height of all high school basketball players. You want to be [latex]98\%[/latex] confident with a margin of error of [latex]3.75[/latex]. From a small pilot study, you estimate the standard deviation to be [latex]7.5[/latex] cm. How large a sample do you need to take to achieve the desired level of accuracy?
Click to see Solution
| Function | norm.s.inv |
|---|---|
| Field 1 | 0.99 |
| Answer | 2.3263… |
[latex]\begin{eqnarray*}n & = & \left(\frac{z \times \sigma}{E}\right)^2 \\ & = & \left(\frac{2.3263... \times 7.5}{3.75}\right)^2 \\ & = & 21.6487... \\& \Rightarrow & 22 \text{ high school basketball players}\end{eqnarray*}[/latex]
Calculating the Sample Size for a Population Proportion
The margin of error [latex]E[/latex] for a confidence interval for a population proportion is
[latex]\displaystyle{E=z \times \sqrt{\frac{p \times (1-p)}{n}}}[/latex]
where [latex]z[/latex] is the [latex]z[/latex]-score so that the area under the standard normal distribution in between [latex]-z[/latex] and [latex]z[/latex] is the confidence level [latex]C[/latex].
Rearranging this formula, we get a formula for the sample size [latex]n[/latex]:
[latex]\displaystyle{n=p \times (1-p) \times \left(\frac{z}{E}\right)^2}[/latex]
In order to use this formula, we need values for [latex]z[/latex], [latex]E[/latex] and [latex]p[/latex]:
- The value for [latex]z[/latex] is determined by the confidence level of the interval, calculated the same way we calculate the [latex]z[/latex]-score for a confidence interval.
- The value for the margin of error [latex]E[/latex] is set as the predetermined acceptable error, or tolerance, for the difference between the sample proportion [latex]\hat{p}[/latex] and the population proportion [latex]p[/latex]. In other words, [latex]E[/latex] is set to the maximum allowable width of the confidence interval.
- An estimate for the population proportion [latex]p[/latex]. If no estimate for the population proportion is provided, we use [latex]p=0.5[/latex].
NOTES
- The value of [latex]n[/latex] determined from the formula is the minimum sample size required to achieve the desired level of confidence. The sample size [latex]n[/latex] is a count, and so is an integer. It would be unusual for the value of [latex]n[/latex] generated by the formula to be an integer. Because [latex]n[/latex] is the minimum sample size required, we must round the output from the formula up to the next integer. If we round the value of [latex]n[/latex] down, the sample size will be below the minimum required sample size.
- After we find the sample size [latex]n[/latex] and collect the data for the sample, we use the appropriate confidence interval formula and the sample proportion from the actual sample.
- By using [latex]0.5[/latex] as an estimate for [latex]p[/latex] in the sample size formula, we will get the largest required sample size for the confidence level and margin of error selected. This is true because of all combinations of two fractions (the values of [latex]p[/latex] and [latex]1-p[/latex]) that add to one, and the largest multiple is when each is [latex]0.5[/latex]. Without any other information concerning the population parameter [latex]p[/latex], this is the common practice. This may result in oversampling, but certainly not under-sampling.
There is an interesting trade-off between the level of confidence and the sample size that shows up here when considering the cost of sampling. The table below shows the appropriate sample size at different levels of confidence and different margins of error, assuming [latex]p=0.5[/latex]. Looking at each row, we can see that for the same margin of error, a higher level of confidence requires a larger sample size. Similarly, looking at each column, we can see that for the same confidence level, a smaller margin of error requires a larger sample size.
| Required Sample Size (90%) | Required Sample Size (95%) | Margin of Error |
|---|---|---|
| 1691 | 2401 | 2% |
| 752 | 1067 | 3% |
| 271 | 384 | 5% |
| 68 | 96 | 10% |
EXAMPLE
Suppose a mobile phone company wants to determine the current percentage of customers aged 50+ who use text messaging on their cell phones. How many customers aged 50+ should the company survey in order to be [latex]90\%[/latex] confident with a margin of error of [latex]3\%[/latex]?
Solution
To find the sample size, we need to find the [latex]z[/latex]-score for the [latex]90\%[/latex] confidence interval. This means that we need to find the [latex]z[/latex]-score from the standard normal distribution so that the entire area to the left of [latex]z[/latex] is [latex]\displaystyle{0.90+\frac{1-0.90}{2}=0.95}[/latex].
| Function | norm.s.inv |
|---|---|
| Field 1 | 0.95 |
| Answer | 1.6448… |
So [latex]z=1.6.448....[/latex]. From the question [latex]E=0.03[/latex]. Because no estimate of the population proportion is given, [latex]p=0.5[/latex].
[latex]\begin{eqnarray*}n & = & p \times (1-p) \times \left(\frac{z }{E}\right)^2 \\ & = & 0.5 \times (1-0.5) \times \left( \frac{1.6448...}{0.03}\right)^2 \\ & = & 751.539... \\ & \Rightarrow & 752 \text{ customers age 50+}\end{eqnarray*}[/latex]
[latex]752[/latex] customers aged 50+ must be surveyed to achieve the desired accuracy.
NOTE
Remember to round the value for the sample size UP to the next integer. This ensures that the sample size is large enough. Do not forget to include appropriate units with the sample size.
TRY IT
Suppose an internet marketing company wants to determine the percentage of customers who click on ads on their smartphones. How many customers should the company survey in order to be [latex]94\%[/latex] confident that the estimated proportion is within [latex]5\%[/latex] of the population proportion of customers who click on ads on their smartphones?
Click to see Solution
| Function | norm.s.inv |
|---|---|
| Field 1 | 0.97 |
| Answer | 1.8807… |
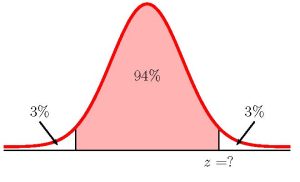[latex]\begin{eqnarray*}n & = & p \times (1-p) \times \left(\frac{z}{E}\right)^2 \\ & = & 0.5 \times (1-0.5) \times \left(\frac{1.8807...}{0.05}\right)^2 \\ & = & 353.738... \\& \Rightarrow & 354 \text{ customers}\end{eqnarray*}[/latex]
Video: “Excel Statistics 87: Sample Size for Confidence Intervals” by excelisfun [7:55] is licensed under the Standard YouTube License.Transcript and closed captions available on YouTube.
Exercises
- The average height of young adult males has a normal distribution with a standard deviation of [latex]6.25[/latex] cm. You want to estimate the mean height of students at your college or university to within [latex]3[/latex] cm with [latex]93\%[/latex] confidence. How many male students must you measure?
Click to see Answer
[latex]15[/latex] male students
- A researcher wants to estimate the mean weight of apples in an orchard. The researcher wants to be [latex]94\%[/latex] confident with a margin of error of [latex]30[/latex] gram. The research takes a small sample of apples and estimates the standard deviation to be [latex]120[/latex] grams. How many apples should the research sample to achieve the required accuracy?
Click to see Answer
[latex]57[/latex] apples
- An events coordinator for a local arena wants to estimate the mean ticket price for an upcoming event. She wants to be within [latex]\$2[/latex] of the actual mean with [latex]99\%[/latex] confidence. The coordinator does not have an estimate for the standard deviation of the ticket prices, but she does know that the tickets range in price from [latex]\$25[/latex] to [latex]\$75[/latex]. How many tickets should the coordinator sample to achieve the required accuracy?
Click to see Answer
[latex]260[/latex] tickets
- A marketer working for a large e-commerce company wants to estimate the mean amount of time a customer spends on the company’s website. Based on a previous study, the marketer estimates the standard deviation to be approximately [latex]4[/latex] minutes and [latex]15[/latex] seconds. How many customers should the marketer sample if they want to be [latex]96\%[/latex] confident with a margin of error of [latex]45[/latex] seconds?
Click to see Answer
[latex]136[/latex] customers
- A human resources manager for a very large company wants to estimate the mean length of employment for the company’s employees. Currently, the HR manager knows that the length of employment for employees ranges from [latex]2[/latex] months to [latex]30[/latex] years. How large a sample does the HR manager need to collect in order to be within [latex]10[/latex] months of the actual mean with [latex]97\%[/latex] confidence?
Click to see Answer
[latex]434[/latex] employees
- Insurance companies are interested in knowing the percentage of drivers who always buckle up before riding in a car.
- When designing a study to determine this population proportion, what is the minimum number you would need to survey to be [latex]95\%[/latex] confident that the population proportion is estimated to be within [latex]3\%[/latex]?
- If it were later determined that it was important to be more than [latex]95\%[/latex] confident and a new survey was commissioned, how would that affect the minimum number you would need to survey? Why?
Click to see Answer
- [latex]752[/latex] drivers
- The sample size would increase because a larger sample is required for a higher confidence. In this case, the minimum sample size is [latex]1068[/latex] drivers.
- You plan to conduct a survey on your college campus to learn about the political awareness of students. You want to estimate the true proportion of college students on your campus who voted in the last federal election with [latex]97\%[/latex] confidence and a margin of error of [latex]5\%[/latex]. How many students must you interview?
Click to see Answer
[latex]471[/latex] students
- The quality control inspector at a company that produces microchips wants to estimate the proportion of defective microchips the company produces. The inspector knows from experience that no more than [latex]7\%[/latex] of the microchips produced are defective. The inspector wants a margin of error of [latex]2\%[/latex]. What size sample should the inspector take in order to be [latex]95\%[/latex] confident of the result?
Click to see Answer
[latex]626[/latex] microchips
- A major airline wants to estimate the proportion of their flights that arrive late to their destination. Currently, the airline estimates that at least [latex]20\%[/latex] of their flights arrive late. How large a sample does the airline need to collect to be within [latex]6\%[/latex] of the actual proportion with [latex]98\%[/latex] confidence?
Click to see Answer
[latex]241[/latex] flights
- A financial planner wants to estimate the proportion of a city’s residents who make regular contributions to a retirement fund. The financial planner wants to be within [latex]8\%[/latex] of the actual proportion with [latex]94\%[/latex] confidence. How large a sample should the planner collect?
Click to see Answer
[latex]139[/latex] residents
“7.5 Calculating the Sample Size for a Confidence Interval” and “7.6 Exercises” from Introduction to Statistics by Valerie Watts is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.
