"

12.2 Scatter Diagrams

LEARNING OBJECTIVES

  • Define independent and dependent variables.
  • Create and analyze scatter diagrams.

Independent and Dependent Variables

An independent variable (or the [latex]x[/latex]-variable) is called the explanatory or predictor variable. The independent variable is used for prediction and provides the basis for estimation. The independent variable may be thought of as the input value and is used to determine the output value (the value of the dependent variable).

A dependent variable (or the [latex]y[/latex]-variable) is called the response or outcome variable. The dependent variable is the variable being predicted or estimated based on the value of the independent variable. The dependent variable may be thought of as the output value and is determined by the input value (the value of the independent variable).

EXAMPLE

Svetlana tutors to make extra money for college. For each tutoring session, she charges a one-time fee of [latex]\$25[/latex] plus [latex]\$25[/latex] per hour of tutoring. The two variables are the number of hours per session and the amount of money earned per session.

  • The number of hours per session is the independent variable because it can be used to predict the value of the other variable (the amount of money earned per session).
  • The amount of money earned per session is the dependent variable because its value can be determined from the value of the other variable (the number of hours per session).

Scatter Diagrams

Before we begin discussing correlation and linear regression, we need to consider ways to display the relationship between the independent variable [latex]x[/latex] and the dependent variable [latex]y[/latex]. The most common and easiest way to illustrate the relationship between the two variables is with a scatter diagram.

A scatter diagram (or scatter plot) is a graphical presentation of the relationship between two numerical variables. Each point on the scatter diagram represents the values of two variables. The [latex]x[/latex]-coordinate is the value of the independent variable, and the [latex]y[/latex]-coordinate is the value of the corresponding dependent variable.

To construct a scatter diagram:

  1. Identify the independent and dependent variables.
  2. Assign the independent variable to the horizontal or [latex]x[/latex]-axis.  Assign the dependent variable to the vertical or [latex]y[/latex]-axis.
  3. Plot the points on an [latex](x,y)[/latex]-grid.
  4. Label the axes, including both the variable names and units.
  5. Include a chart title.  A common chart title is independent variable vs dependent variable, using the actual names of the variables.

EXAMPLE

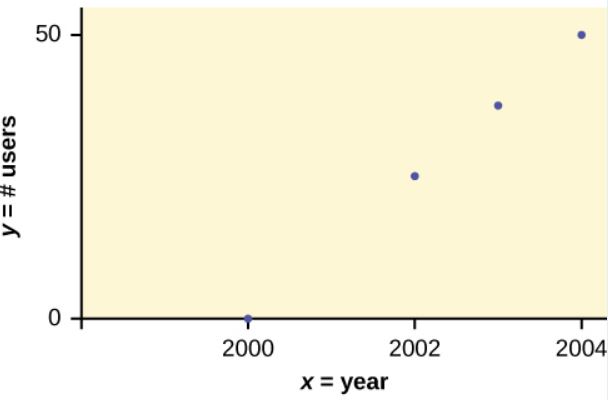
In Europe and Asia, m-commerce is popular. M-commerce users have special mobile phones that work like electronic wallets as well as provide phone and internet services. Users can do everything from paying for parking to buying a TV set or soda from a machine to banking to checking sports scores on the internet. Data for the number of users from years 2000 through 2004 is given in the table below.

Year Number of Users (in millions)
2000 0.5
2002 20.0
2003 33.0
2004 47.0

Which variable is the independent variable? Which variable is the dependent variable? Construct a scatter diagram for this data.

Solution

  • The year is the independent variable because it can be used to predict the value of the other variable (the number of users).
  • The number of users is the dependent variable because its value can be determined from the value of the other variable (year).

This is a scatter plot for the data provided. The x-axis represents the year and the y-axis represents the number of m-commerce users in millions. There are four points plotted, at (2000, 0.5), (2002, 20.0), (2003, 33.0), (2004, 47.0).

TRY IT

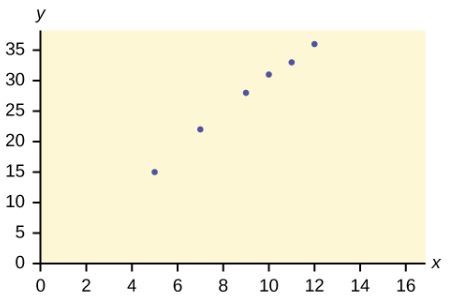
Amelia plays basketball for her high school. She wants to improve her play so she can compete at the college level. The table below records the number of hours she spends practicing her jump shot before a game and the number of points she scored in the following game.

Hours Spent Practicing Jump Shot Points Scored in Game
5 15
7 22
9 28
10 31
11 33
12 36

Which variable is the independent variable? Which variable is the dependent variable? Construct a scatter diagram for this data.

 

Click to see Solution

 

  • The hours spent practicing jump shots is the independent variable because it can be used to predict the value of the other variable (points scored in the game).
  • The points scored in a game are the dependent variable because its value can be determined from the value of the other variable (hours spent practicing jump shots).

https://assets.coursehero.com/study-guides/lumen/images/introstats1/scatter-plots/03l5-fu4g757i2" alt="This is a scatter plot for the data provided. The x-axis is labeled in increments of 2 from 0 - 16. The y-axis is labeled in increments of 5 from 0 - 35.

CONSTRUCTING A SCATTER DIAGRAM IN EXCEL

To create a scatter diagram in Excel:

  1. Identify the independent and dependent variables.
  2. If necessary, rearrange the columns so that the column containing the independent variable data is on the left and the dependent variable is on the right.  (Excel always places the variable on the left on the horizontal axis.)
  3. Go to the Insert tab.  In the Charts group, click on Scatter.  Select the scatter diagram with only markers (points).
  4. Using the chart tools, add axis titles, including both the variable names and units on the axes.
  5. Using the chart tools, add a chart title. A common chart title is independent variable vs dependent variable, using the actual names of the variables.

Visit the Microsoft page for more information about creating a scatter diagram in Excel.

A scatter diagram shows the direction of the relationship between the independent and dependent variables. That is, a scatter diagram shows if the points are, in general, rising or falling as we read from left to right across the graph.

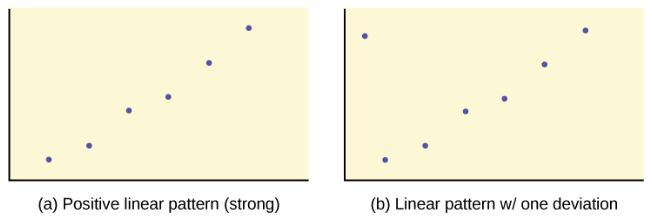
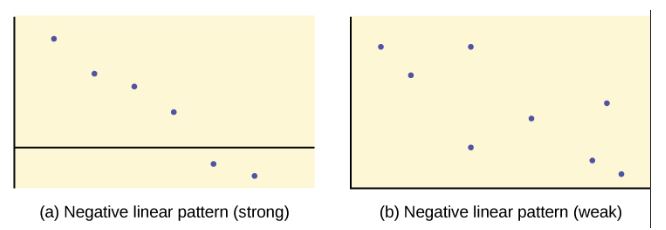
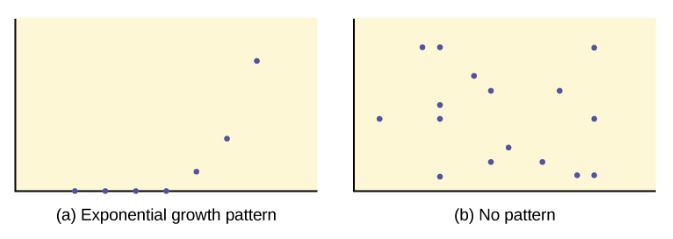
We can determine the strength of the relationship by looking at the scatter diagram to see how close the points are to a line, a power function, an exponential function, or to some other type of function. The stronger the relationship, the better the corresponding regression model (linear, exponential, etc.) will be at predicting values of the dependent variable.

When we look at a scatter diagram, we want to notice the overall pattern and any deviations from the pattern. The scatter diagrams shown below illustrate these concepts.

The first graph is a scatter plot with 6 points plotted. The points form a pattern that moves upward to the right, almost in a straight line. The second graph is a scatter plot with the same 6 points as the first graph. A 7th point is plotted in the top left corner of the quadrant. It falls outside the general pattern set by the other 6 points.https://assets.coursehero.com/study-guides/lumen/images/introstats1/scatter-plots/g7zh-n55g757i4" alt="The first graph is a scatter plot with 6 points plotted. The points form a pattern that moves downward to the right, almost in a straight line. The second graph is a scatter plot of 8 points. These points form a general downward pattern, but the point do not align in a tight pattern.The first graph is a scatter plot of 7 points in an exponential pattern. The pattern of the points begins along the x-axis and curves steeply upward to the right side of the quadrant. The second graph shows a scatter plot with many points scattered everywhere, exhibiting no pattern. "

In this chapter, we are only concerned with the strength and direction of the linear relationship between the independent and dependent variables. In the next section, we will learn about a numerical measure, the correlation coefficient, that measures the strength and direction of the linear relationship.

Because linear patterns are quite common, we are interested in scatter diagrams that show a linear pattern. The linear relationship is strong if the points are close to a straight line, except in the case of a horizontal line where there is no relationship. If a scatter diagram shows a linear relationship, we would like to create a model based on this apparent linear relationship. This model is constructed through a process called simple linear regression. However, we only calculate a regression line if one of the variables, [latex]x[/latex], helps to explain or predict the other variable, [latex]y[/latex].  If [latex]x[/latex] is the independent variable and [latex]y[/latex] is the dependent variable, then we can use a regression line to predict a value for [latex]y[/latex] for a given value of [latex]x[/latex].

Video: “Basic Excel Business Analytics #44: Intro To Linear Regression & Scatter Chart” by excelisfun [15:46] is licensed under the Standard YouTube License.Transcript and closed captions available on YouTube.

Exercises

  1. The table below contains real data for the first two decades of AIDS cases.
    Year Number of AIDS Cases
    1981 319
    1982 1,170
    1983 3,076
    1984 6,240
    1985 11,776
    1986 19,032
    1987 28,564
    1988 35,447
    1989 42,674
    1990 48,634
    1991 59,660
    1992 78,530
    1993 78,834
    1994 71,874
    1995 68,505
    1996 59,347
    1997 47,149
    1998 38,393
    1999 25,174
    2000 25,522
    2001 25,643
    2002 26,464
    1. Which variable is the independent variable, and which variable is the dependent variable?
    2. Construct a scatter diagram for this data.
    Click to see Answer
    1. Independent: Year; Dependent: Number of AIDS Cases
    2. The scatter plot of number of aids cases on the y-axis and year on the x-axis.

     

  2. A specialty cleaning company charges an equipment fee and an hourly labour fee. A linear equation that expresses the total amount of the fee the company charges for each session is [latex]y=50+100x[/latex].
    1. What are the independent and dependent variables?
    2. What is the [latex]y[/latex]-intercept? Interpret the [latex]y[/latex]-intercept using complete sentences.
    3. What is the slope? Interpret the slope using complete sentences.
    Click to see Answer
    1. Independent: Number of Hours of Labour; Dependent: Total Amount of Fee
    2. [latex]50[/latex]. When the number of hours of labour is [latex]0[/latex], the total amount is [latex]\$50[/latex].
    3. [latex]100[/latex]. For each extra hour of labour, the total amount increases by [latex]\$100[/latex].

     

  3. Due to erosion, a river shoreline is losing several thousand pounds of soil each year. A linear equation that expresses the total amount of soil lost per year is [latex]y=12,000x[/latex].
    1. What are the independent and dependent variables?
    2. How many pounds of soil does the shoreline lose in a year?
    3. What is the [latex]y[/latex]-intercept? Interpret its meaning.
    Click to see Answer
    1. Independent: Year; Dependent: Amount of Soil Lost
    2. [latex]12,000[/latex]
    3. [latex]0[/latex]. There is no soil lost in year [latex]0[/latex].

     

  4. For each of the following situations, state the independent variable and the dependent variable.
    1. A study is done to determine if elderly drivers are involved in more motor vehicle fatalities than other drivers. The number of fatalities per [latex]100,000[/latex] drivers is compared to the age of drivers.
    2. A study is done to determine if the weekly grocery bill changes based on the number of family members.
    3. Insurance companies base life insurance premiums partially on the age of the applicant.
    4. Utility bills vary according to power consumption.
    5. A study is done to determine if a higher education reduces the crime rate in a population.
    Click to see Answer
    1. Independent: Age of driver; Dependent: Number of fatalities
    2. Independent: Number of family members; Dependent: Weekly grocery bill
    3. Independent: Age of applicant; Dependent: Life insurance premium
    4. Independent: Power consumption; Dependent: Amount of utility bill
    5. Independent: Years of education; Dependent: Crime rate

     

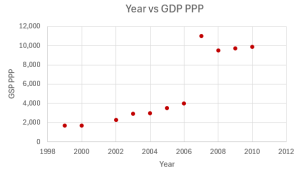
  5. The Gross Domestic Product Purchasing Power Parity is an indication of a country’s currency value compared to another country. The table below shows the GDP PPP of Cuba as compared to US dollars. Construct a scatter plot of the data.
    Year Cuba’s PPP
    1999 1,700
    2000 1,700
    2002 2,300
    2003 2,900
    2004 3,000
    2005 3,500
    2006 4,000
    2007 11,000
    2008 9,500
    2009 9,700
    2010 9,900
    Click to see Answer

    The scatter plot of GDP PPP on the y-axis and year on the x-axis.

     

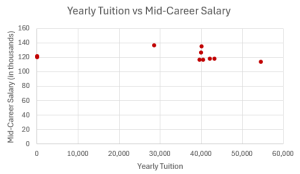
  6. Does the higher cost of tuition translate into higher-paying jobs? The table lists the top ten colleges based on mid-career salary and the associated yearly tuition costs. Construct a scatter plot of the data.
    School Mid-Career Salary (in thousands) Yearly Tuition
    Princeton 137 28,540
    Harvey Mudd 135 40,133
    CalTech 127 39,900
    US Naval Academy 122 0
    West Point 120 0
    MIT 118 42,050
    Lehigh University 118 43,220
    NYU-Poly 117 39,565
    Babson College 117 40,400
    Stanford 114 54,506
    Click to see Answer

    The scatter plot of mid-career salary in thousands on the y-axis and yearly tuition on the x-axis.

     

  7. The table below gives the percent of workers who are paid hourly rates for the years 1979 to 1992.
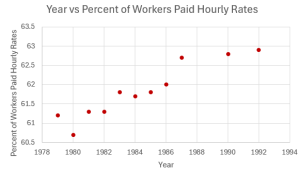
    Year Percent of Workers Paid Hourly Rates
    1979 61.2
    1980 60.7
    1981 61.3
    1982 61.3
    1983 61.8
    1984 61.7
    1985 61.8
    1986 62.0
    1987 62.7
    1990 62.8
    1992 62.9
    1. Decide which variable should be the independent variable and which should be the dependent variable.
    2. Draw a scatter plot of the ordered pairs.
    Click to see Answer
    1. Independent: year; Dependent: percent of workers paid hourly rate
    2. The scatter plot of percent of workers paid hourly rate on the y-axis and year on the x-axis.

     

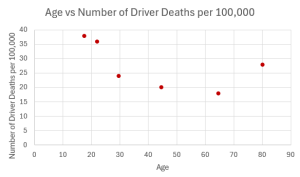
  8. Recently, the annual number of driver deaths per [latex]100,000[/latex] for the selected age groups was as follows:
    Age Number of Driver Deaths per [latex]100,000[/latex]
    17.5 38
    22 36
    29.5 24
    44.5 20
    64.5 18
    80 28
    1. Decide which variable should be the independent variable and which should be the dependent variable.
    2. Draw a scatter plot of the data.
    Click to see Answer
    1. Independent: age; Dependent: number of driver deaths per [latex]100,000[/latex]
    2. The scatter plot of number of driver deaths per 100,000 on the y-axis and age on the x-axis.

     

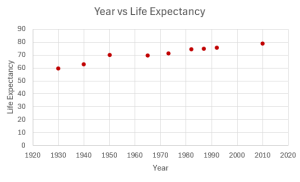
  9. The table below shows the life expectancy for an individual born in the United States in certain years.
    Year of Birth Life Expectancy
    1930 59.7
    1940 62.9
    1950 70.2
    1965 69.7
    1973 71.4
    1982 74.5
    1987 75
    1992 75.7
    2010 78.7
    1. Decide which variable should be the independent variable and which should be the dependent variable.
    2. Draw a scatter plot of the ordered pairs.
    Click to see Answer
    1. Independent: year; Dependent: life expectancy
    2. The scatter plot of life expectancy on the y-axis and year on the x-axis.

     

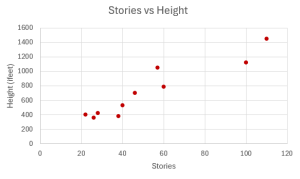
  10. The height (sidewalk to roof) of notable tall buildings in America is compared to the number of stories of the building (beginning at street level).
    Height (in feet) Number of Stories
    1,050 57
    428 28
    362 26
    529 40
    790 60
    401 22
    380 38
    1,454 110
    1,127 100
    700 46
    1. Decide which variable should be the independent variable and which should be the dependent variable.
    2. Draw the scatter diagram for this data.
    Click to see Answer
    1. Independent: number of stories; Dependent: height
    2. The scatter plot of height on the y-axis and stories on the x-axis.

     

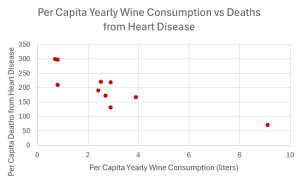
  11. The following table shows data on average per capita wine consumption and heart disease rate in a random sample of 10 countries.
    Per Capita Yearly Wine Consumption in Liters Per Capita Death from Heart Disease
    2.5 221
    3.9 167
    2.9 131
    2.4 191
    2.9 220
    0.8 297
    9.1 71
    2.7 172
    0.8 211
    0.7 300
    1. Decide which variable should be the independent variable and which should be the dependent variable.
    2. Draw a scatter plot of the ordered pairs.
    Click to see Answer
    1. Independent: yearly wine consumption; Dependent: death from heart disease
    2. The scatter plot of death from heart disease on the y-axis and yearly wine consumption on the x-axis.

     

  12. The following table consists of one student athlete’s time (in minutes) to swim 2000 meters and the student’s heart rate (beats per minute) after swimming on a random sample of 10 days.
    Swim Time Heart Rate
    34.12 144
    35.72 152
    34.72 124
    34.05 140
    34.13 152
    35.73 146
    36.17 128
    35.57 136
    35.37 144
    35.57 148
    1. Decide which variable should be the independent variable and which should be the dependent variable.
    2. Draw a scatter plot of the ordered pairs.
    Click to see Answer
    1. Independent: swim time; Dependent: heart rate
    2. The scatter plot of heart rate on the y-axis and swim time on the x-axis.

     

“12.3 Scatter Diagrams” and “12.8 Exercises” from Introduction to Statistics by Valerie Watts is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Introduction to Statistics - Second Edition Copyright © 2025 by Valerie Watts is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.

Share This Book