"

8.4 Hypothesis Tests for a Population Mean with Known Population Standard Deviation

LEARNING OBJECTIVES

  • Conduct and interpret hypothesis tests for a population mean with known population standard deviation.

Some notes about conducting a hypothesis test:

  • The null hypothesis [latex]H_0[/latex] is always an “equal to.”  The null hypothesis is the original claim about the population parameter.
  • The alternative hypothesis [latex]H_a[/latex] is a “less than,” “greater than,” or “not equal to.”  The form of the alternative hypothesis depends on the context of the question.
  • The form of the alternative hypothesis tells us if the test is left-tail, right-tail, or two-tail. The alternative hypothesis is the key to conducting the test and finding the correct [latex]p-\text{value}[/latex].
    • If the alternative hypothesis is a “less than”, then the test is left-tail. The [latex]p-\text{value}[/latex] is the area in the left-tail of the distribution.
    • If the alternative hypothesis is a “greater than”, then the test is right-tail. The [latex]p-\text{value}[/latex] is the area in the right-tail of the distribution.
    • If the alternative hypothesis is a “not equal to”, then the test is two-tail. The [latex]p-\text{value}[/latex] is the sum of the area in the two-tails of the distribution. Each tail represents exactly half of the [latex]p-\text{value}[/latex].
  • Think about the meaning of the [latex]p-\text{value}[/latex]. A data analyst (and anyone else) should have more confidence that they made the correct decision to reject the null hypothesis with a smaller [latex]p-\text{value}[/latex] (for example, [latex]0.001[/latex] as opposed to [latex]0.04[/latex]) even if using a significance level of [latex]0.05[/latex]. Similarly, for a large [latex]p-\text{value}[/latex] such as [latex]0.4[/latex], as opposed to a [latex]p-\text{value}[/latex] of [latex]0.056[/latex] (a significance level of [latex]0.05[/latex] is less than either number), a data analyst should have more confidence that they made the correct decision in not rejecting the null hypothesis. This makes the data analyst use judgment rather than mindlessly applying rules.
  • The significance level must be identified before collecting the sample data and conducting the test. Generally, the significance level will be included in the question. If no significance level is given, a common standard is to use a significance level of [latex]5\%[/latex].
  • An alternative approach for hypothesis testing is to use what is called the critical value approach. In this book, we will only use the [latex]p-\text{value}[/latex] approach. Some of the videos below may mention the critical value approach, but this approach will not be used in this book.

EXAMPLE

Suppose the hypotheses for a hypothesis test are:

[latex]\begin{eqnarray*}H_0:&&\mu=5\\H_a:&&\mu\lt 5\end{eqnarray*}[/latex]

Because the alternative hypothesis is a [latex]\lt[/latex], this is a left-tailed test. The [latex]p-\text{value}[/latex] is the area in the left-tail of the distribution.

Normal distribution curve of a single population mean with a value of 5 on the x-axis and the p-value points to the area on the left tail of the curve.

EXAMPLE

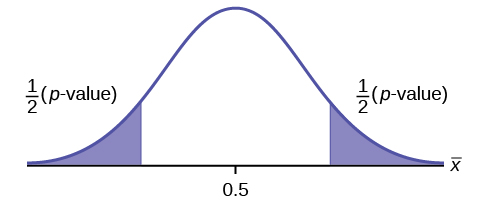
Suppose the hypotheses for a hypothesis test are:

[latex]\begin{eqnarray*}H_0:&&\mu=0.5\\H_a:&&\mu\neq 0.5\end{eqnarray*}[/latex]

Because the alternative hypothesis is a [latex]\neq[/latex], this is a two-tailed test. The [latex]p-\text{value}[/latex] is the sum of the areas in the two tails of the distribution. Each tail contains exactly half of the [latex]p-\text{value}[/latex].

Normal distribution curve of a single population mean with a value of 0.5 on the x-axis. The p-value formulas, 1/2(p-value), for a two-tailed test is shown for the areas on the left and right tails of the curve.

EXAMPLE

Suppose the hypotheses for a hypothesis test are:

[latex]\begin{eqnarray*}H_0:&&\mu=10\\H_a:&&\mu\lt 10\end{eqnarray*}[/latex]

Because the alternative hypothesis is a [latex]\lt[/latex], this is a left-tailed test. The [latex]p-\text{value}[/latex] is the area in the left-tail of the distribution.

Normal distribution curve of a single population mean with a value of 10 on the x-axis and the p-value points to the area on the left tail of the curve.

Conducting a Hypothesis Test for a Population Mean with a Known Population Standard Deviation

Follow these steps to perform a hypothesis test on a population mean with a known population standard deviation:

  1. Write down the null and alternative hypotheses in terms of the population mean [latex]\mu[/latex]. Include appropriate units with the values of the mean.
  2. Use the form of the alternative hypothesis to determine if the test is left-tailed, right-tailed, or two-tailed.
  3. Collect the sample information for the test and identify the significance level [latex]\alpha[/latex].
  4. When the population standard deviation is known, we use a normal distribution with [latex]\displaystyle{z=\frac{\overline{x}-\mu}{\frac{\sigma}{\sqrt{n}}}}[/latex] to find the [latex]p-\text{value}[/latex]. The [latex]p-\text{value}[/latex] is the area in the corresponding tail of the normal distribution.
  5. Compare the [latex]p-\text{value}[/latex] to the significance level and state the outcome of the test.
    • If [latex]p-\text{value}\leq\alpha[/latex], reject [latex]H_0[/latex] in favour of [latex]H_a[/latex].
      • The results of the sample data are significant. There is sufficient evidence to conclude that the null hypothesis [latex]H_0[/latex] is an incorrect belief and that the alternative hypothesis [latex]H_a[/latex] is most likely correct.
    • If [latex]p-\text{value}\gt\alpha[/latex], do not reject [latex]H_0[/latex].
      • The results of the sample data are not significant. There is not sufficient evidence to conclude that the alternative hypothesis [latex]H_a[/latex] may be correct.
  6. Write down a concluding sentence specific to the context of the question.

USING EXCEL TO CALCULATE THE [latex]\color{white}{p-\text{value}}[/latex] FOR A HYPOTHESIS TEST ON A POPULATION MEAN WITH KNOWN POPULATION STANDARD DEVIATION

The [latex]p-\text{value}[/latex] for a hypothesis test on a population mean is the area in the tail(s) of the distribution of the sample mean. When the population standard deviation is known, use the normal distribution to find the [latex]p-\text{value}[/latex].

The [latex]p-\text{value}[/latex] is the area in the tail(s) of a normal distribution, so the norm.dist(x,[latex]\mu[/latex],[latex]\sigma[/latex],logic operator) function can be used to calculate the [latex]p-\text{value}[/latex].

  • For x, enter the value for [latex]\overline{x}[/latex].
  • For [latex]\mu[/latex], enter the mean of the sample means [latex]\mu[/latex]. Note: Because the test is run assuming the null hypothesis is true, the value for [latex]\mu[/latex] is the claim from the null hypothesis.
  • For [latex]\sigma[/latex], enter the standard error of the mean [latex]\displaystyle{\frac{\sigma}{\sqrt{n}}}[/latex].
  • For the logic operator, enter true. Note:  Because we are calculating the area under the curve, we always enter true for the logic operator.

Use the appropriate technique with the norm.dist function to find the area in the left-tail or the area in the right-tail.

EXAMPLE

Jeffrey, as an eight-year-old, established a mean time of [latex]16.43[/latex] seconds with a standard deviation of [latex]0.8[/latex] seconds for swimming the 25-meter freestyle. His dad, Frank, thought that Jeffrey could swim the 25-meter freestyle faster using goggles. Frank bought Jeffrey a new pair of goggles and timed Jeffrey swimming the 25-meter freestyle [latex]15[/latex] different times. In the sample of [latex]15[/latex] swims, Jeffrey’s mean time was [latex]16[/latex] seconds. Frank thought that the goggles helped Jeffrey swim faster than [latex]16.43[/latex] seconds. At the [latex]5\%[/latex] significance level, did Jeffrey swim faster wearing the goggles? Assume that the swim times for the 25-meter freestyle are normally distributed.

Solution

Hypotheses:

[latex]\begin{eqnarray*}H_0:&&\mu=16.43\text{ seconds}\\H_a:&&\mu\lt 16.43\text{ seconds}\end{eqnarray*}[/latex]

[latex]p-\text{value}[/latex] : 

From the question, we have [latex]n=15[/latex], [latex]\overline{x}=16[/latex], [latex]\sigma=0.8[/latex] and [latex]\alpha=0.05[/latex].

This is a test on a population mean where the population standard deviation is known ([latex]\sigma=0.8[/latex]). So, we use a normal distribution to calculate the [latex]p-\text{value}[/latex]. Because the alternative hypothesis is a [latex]\lt[/latex], the [latex]p-\text{value}[/latex] is the area in the left-tail of the distribution.

This is a normal distribution curve. On the left side of the center a vertical line extends to the curve with the area to the left of this vertical line shaded. The p-value equals the area of this shaded region.
Function  norm.dist
Field 1 16
Field 2 16.43
Field 3 0.8/sqrt(15)
Field 4 true
Answer 0.0187

So the [latex]p-\text{value}=0.0187[/latex].

Conclusion:

Because [latex]p-\text{value}=0.0187\lt 0.05=\alpha[/latex], we reject the null hypothesis in favour of the alternative hypothesis. At the [latex]5\%[/latex] significance level, there is enough evidence to suggest that Jeffrey’s mean swim time with the goggles is less than [latex]16.43[/latex] seconds.

NOTES

  1. The null hypothesis [latex]\mu=16.43[/latex] is the claim that Jeffrey’s mean swim time with the goggles is [latex]16.43[/latex] seconds (the same as it is without the googles).
  2. The alternative hypothesis [latex]\mu\lt 16.43[/latex] is the claim that Jeffrey’s swim time with the goggles is less than [latex]16.43[/latex] seconds.
  3. The [latex]p-\text{value}[/latex] is the area in the left tail of the sampling distribution, to the left of [latex]\overline{x}=16[/latex]. In the calculation of the [latex]p-\text{value}[/latex] :
    • The function is norm.dist because we are finding the area in the left tail of a normal distribution.
    • Field 1 is the value of [latex]\overline{x}[/latex]
    • Field 2 is the value of [latex]\mu[/latex] from the null hypothesis. Remember, we run the test assuming the null hypothesis is true, so that means we assume [latex]\mu=16.43[/latex].
    • Field 3 is the standard deviation for the sample means [latex]\displaystyle{\frac{\sigma}{\sqrt{n}}}[/latex]. Note that we are not using the standard deviation from the population ([latex]\sigma=0.8[/latex]). This is because the [latex]p-\text{value}[/latex]  is the area under the curve of the distribution of the sample means, not the distribution of the population.
  4. The [latex]p-\text{value}[/latex] of [latex]0.0187[/latex] tells us that under the assumption that Jeffrey’s mean swim time with goggles is [latex]16.43[/latex] seconds (the null hypothesis), there is only a [latex]1.87\%[/latex] chance that the mean time for the [latex]15[/latex] sample swims is [latex]16[/latex] seconds or less. This is a small probability, and so it is unlikely to happen, assuming the null hypothesis is true. This suggests that the assumption that the null hypothesis is true is most likely incorrect, and so the conclusion of the test is to reject the null hypothesis in favour of the alternative hypothesis.
  5. The Type I error for this problem is to conclude that Jeffrey swims the 25-meter freestyle, on average, in less than [latex]16.43[/latex] seconds (the alternative hypothesis) when, in fact, he actually swims the 25-meter freestyle, on average, in [latex]16.43[/latex] seconds (the null hypothesis). That is, reject the null hypothesis when the null hypothesis is actually true.
  6. The Type II error for this problem is to conclude that Jeffrey swims the 25-meter freestyle, on average, in [latex]16.43[/latex] seconds (the null hypothesis) when, in fact, he actually swims the 25-meter freestyle, on average, in less than [latex]16.43[/latex] seconds (the alternative hypothesis). That is, do not reject the null hypothesis when the null hypothesis is actually false.

TRY IT

The mean throwing distance of a football for Marco, a high school freshman quarterback, is [latex]40[/latex] yards with a standard deviation of [latex]2[/latex] yards. The team coach tells Marco to adjust his grip to get more distance. The coach records the distances for [latex]20[/latex] throws with the new grip. For the [latex]20[/latex] throws, Marco’s mean distance was [latex]41.5[/latex] yards. The coach thought the different grip helped Marco throw farther than [latex]40[/latex] yards. At the [latex]5\%[/latex] significance level, is Marco’s mean throwing distance higher with the new grip? Assume the throw distances for footballs are normally distributed.

 

Click to see Solution

 

Hypotheses:

[latex]\begin{eqnarray*}H_0:&&\mu=40\text{ yards}\\H_a:&&\mu\gt 40\text{ yards}\end{eqnarray*}[/latex]

[latex]p-\text{value}[/latex]: 

From the question, we have [latex]n=20[/latex], [latex]\overline{x}=41.5[/latex], [latex]\sigma=2[/latex] and [latex]\alpha=0.05[/latex].

This is a test on a population mean where the population standard deviation is known ([latex]\sigma=2[/latex]). So we use a normal distribution to calculate the [latex]p-\text{value}[/latex]. Because the alternative hypothesis is a [latex]\gt[/latex], the [latex]p-\text{value}[/latex] is the area in the right-tail of the distribution.

This is a normal distribution curve. On the right side of the center a vertical line extends to the curve with the area to the right of this vertical line shaded. The p-value equals the area of this shaded region.
Function 1-norm.dist
Field 1 41.5
Field 2 40
Field 3 2/sqrt(20)
Field 4 true
Answer 0.0004

So the [latex]p-\text{value}=0.0004[/latex].

Conclusion:

Because [latex]p-\text{value}=0.0004\lt 0.05=\alpha[/latex], we reject the null hypothesis in favour of the alternative hypothesis. At the [latex]5\%[/latex] significance level, there is enough evidence to suggest that Marco’s mean throwing distance is greater than [latex]40[/latex] yards with the new grip.

NOTES

  1. The null hypothesis [latex]\mu=40[/latex] is the claim that Marco’s mean throwing distance with the new grip is [latex]40[/latex] yards (the same as it is without the new grip).
  2. The alternative hypothesis [latex]\mu\gt 40[/latex] is the claim that Marco’s mean throwing distance with the new grip is greater than [latex]40[/latex] yards.
  3. The [latex]p-\text{value}[/latex]  is the area in the right tail of the normal distribution. To calculate the area in the right-tail of a normal distribution, we use 1-norm.dist.
    • Field 1 is the value of [latex]\overline{x}[/latex]
    • Field 2 is the value of [latex]\mu[/latex] from the null hypothesis.
    • Field 3 is the standard deviation for the sample means [latex]\displaystyle{\frac{\sigma}{\sqrt{n}}}[/latex].
  4. The [latex]p-\text{value}[/latex] of 0.0004 tells us that under the assumption that Marco’s mean throwing distance with the new grip is [latex]40[/latex] yards, there is only a [latex]0.04\%[/latex] chance that the mean throwing distance for the [latex]20[/latex] sample throws is more than [latex]40[/latex] yards. This is a small probability and so is unlikely to happen, assuming the null hypothesis is true. This suggests that the assumption that the null hypothesis is true is most likely incorrect, and so the conclusion of the test is to reject the null hypothesis in favour of the alternative hypothesis.

EXAMPLE

A local college states in its marketing materials that the average age of its first-year students is [latex]18.3[/latex]years with a standard deviation of [latex]3.4[/latex] years. But this information is based on old data and does not take into account that more older adults are returning to college. A researcher at the college believes that the average age of its first-year students has changed. The researcher takes a sample of [latex]50[/latex] first-year students and finds the average age is [latex]19.5[/latex] years. At the [latex]1\%[/latex] significance level, has the average age of the college’s first-year students changed?

Solution

Hypotheses:

[latex]\begin{eqnarray*}H_0:&&\mu=18.3\text{ years}\\H_a:&&\mu\neq 18.3\text{ years}\end{eqnarray*}[/latex]

[latex]p-\text{value}[/latex] : 

From the question, we have [latex]n=50[/latex], [latex]\overline{x}=19.5[/latex], [latex]\sigma=3.4[/latex] and [latex]\alpha=0.01[/latex].

This is a test on a population mean where the population standard deviation is known ([latex]\sigma=3.4[/latex]). In this case, the sample size is greater than [latex]30[/latex]. So we use a normal distribution to calculate the [latex]p-\text{value}[/latex]. Because the alternative hypothesis is a [latex]\neq[/latex], the [latex]p-\text{value}[/latex] is the sum of the area in the tails of the distribution.

This is a normal distribution curve. On the left side of the center a vertical line extends to the curve with the area to the left of this vertical line shaded and labeled as one half of the p-value. On the right side of the center a vertical line extends to the curve with the area to the right of this vertical line shaded and labeled as one half of the p-value. The p-value equals the sum of area of these two shaded regions.

Because there is only one sample, we only have information relating to one of the two tails, either the left tail or the right tail. We need to know if the sample relates to the left tail or right tail because that will determine how we calculate out the area of that tail using the normal distribution. In this case, the sample mean [latex]\overline{x}=19.5[/latex] is greater than the value of the population mean in the null hypothesis [latex]\mu=18.3[/latex] ([latex]\overline{x}=19.5>18.3=\mu[/latex]), so the sample information relates to the right-tail of the normal distribution. This means that we will calculate out the area in the right tail using 1-norm.dist. However, this is a two-tailed test where the [latex]p-\text{value}[/latex] is the sum of the area in the two tails and the area in the right-tail is only one half of the [latex]p-\text{value}[/latex]. The area in the left tail equals the area in the right tail and the [latex]p-\text{value}[/latex] is the sum of these two areas.

Function  1-norm.dist
Field 1 19.5
Field 2 18.3
Field 3 3.4/sqrt(50)
Field 4 true
Answer 0.0063

So the area in the right tail is [latex]0.0063[/latex] and [latex]\frac{1}{2}p-\text{value}=0.0063[/latex]. This is also the area in the left tail, so

[latex]p-\text{value}=0.0063+0.0063=0.0126[/latex]

Conclusion:

Because [latex]p-\text{value}=0.0126\gt 0.01=\alpha[/latex], we do not reject the null hypothesis. At the [latex]1\%[/latex] significance level, there is not enough evidence to suggest that the average age of the college’s first-year students has changed.

NOTES

  1. The null hypothesis [latex]\mu=18.3[/latex] is the claim that the average age of the first-year students is still [latex]18.3[/latex] years.
  2. The alternative hypothesis [latex]\mu\neq 18.3[/latex] is the claim that the average age of the first-year students has changed from [latex]18.3[/latex] years.
  3. In a two-tailed hypothesis test that uses the normal distribution, we will only have sample information relating to one of the two tails. We must determine which of the tails the sample information belongs to, and then calculate out the area in that tail. The area in each tail represents exactly half of the [latex]p-\text{value}[/latex], so the [latex]p-\text{value}[/latex] is the sum of the areas in the two tails.
    • If the sample mean [latex]\overline{x}[/latex] is less than the population mean [latex]\mu[/latex] in the null hypothesis ([latex]\overline{x}\lt\mu[/latex]), then the sample information belongs to the left tail.
      • We use norm.dist([latex]\overline{x}[/latex],[latex]\mu[/latex],[latex]\sigma/\text{sqrt}(n)[/latex],true) to find the area in the left tail. The area in the right tail equals the area in the left tail, so we can find the [latex]p-\text{value}[/latex] by adding the output from this function to itself.
    • If the sample mean [latex]\overline{x}[/latex] is greater than the population mean [latex]\mu[/latex] in the null hypothesis ([latex]\overline{x}\gt\mu[/latex]), then the sample information belongs to the right tail.
      • We use 1-norm.dist([latex]\overline{x}[/latex],[latex]\mu[/latex],[latex]\sigma/\text{sqrt}(n)[/latex],true) to find the area in the right tail.  The area in the left tail equals the area in the right tail, so we can find the [latex]p-\text{value}[/latex] by adding the output from this function to itself.
  4. The [latex]p-\text{value}[/latex] of [latex]0.0126[/latex] is a large probability compared to the [latex]1\%[/latex] significance level, and so is likely to happen assuming the null hypothesis is true. This suggests that the assumption that the null hypothesis is true is most likely correct, and so the conclusion of the test is to not reject the null hypothesis. In other words, the claim that the average age of first-year students is [latex]18.3[/latex] years is most likely correct.

Video: “Excel Statistical Analysis 43: Hypothesis Testing: P-value & Critical Value Methods: 1 Tail Upper” by excelisfun [32:48] is licensed under the Standard YouTube License.Transcript and closed captions available on YouTube.

Video: “Excel Statistical Analysis 44: Hypothesis Testing with Z Distribution, 1 Tail Lower (Left) Test” by excelisfun [10:58] is licensed under the Standard YouTube License.Transcript and closed captions available on YouTube.

Video: “Excel Statistical Analysis 45: Hypothesis Testing with Z Distribution, Two Tail Test Example” by excelisfun [9:56] is licensed under the Standard YouTube License.Transcript and closed captions available on YouTube.

Exercises

  1. A particular brand of tire claims that its deluxe tire averages [latex]50,000[/latex] kilometres before it needs to be replaced. A group of owners believe this number is too high. From past studies of this tire, the standard deviation is known to be [latex]8,000[/latex] kilometres. A survey of owners of that tire design is conducted. From the [latex]35[/latex] tires surveyed, the mean lifespan was [latex]46,500[/latex] kilometres. At the [latex]5\%[/latex] significance level, test if the tire average before the tire needs replacing is less than claimed.
    Click to see Answer
    • Hypotheses: [latex]\begin{eqnarray*}H_0:&&\mu=50,000\text{ km}\\H_a:&&\mu\lt 50,000\text{ km}\end{eqnarray*}[/latex]
    • [latex]p-\text{value}=0.0048[/latex]
    • Conclusion: At the [latex]5\%[/latex] significance level, there is enough evidence to conclude that the tire average before the tire needs replacing is less than [latex]\$50,000[/latex].

     

  2. From generation to generation, the mean age when smokers first start to smoke is [latex]19[/latex] years. However, the standard deviation of that age remains constant of around [latex]2.1[/latex] years. A health researcher wants to know if the mean age when smokers first started smoking has changed. In a survey of [latex]40[/latex] smokers of this generation, the sample mean was [latex]18.1[/latex] years. At the [latex]1\%[/latex] significance level, test the health researcher’s claim.
    Click to see Answer
    • Hypotheses: [latex]\begin{eqnarray*}H_0:&&\mu=19\text{ years}\\H_a:&&\mu\neq 19\text{ years}\end{eqnarray*}[/latex]
    • [latex]p-\text{value}=0.0067[/latex]
    • Conclusion: At the [latex]1\%[/latex] significance level, there is enough evidence to conclude that the mean age when smokers first started smoking has changed.

     

  3. The cost of a daily newspaper varies from city to city. In the past, the mean cost of a daily newspaper was [latex]\$1.00[/latex] with a standard deviation of [latex]\$0.20[/latex]. But a local newspaper publisher believes that the mean cost of a daily newspaper has increased. In a sample of [latex]30[/latex] daily newspapers, the mean cost was [latex]\$1.06[/latex]. At the [latex]1\%[/latex] significance level, has the mean cost of a daily newspaper increased?
    Click to see Answer
    • Hypotheses: [latex]\begin{eqnarray*}H_0:&&\mu=\$1.00\\H_a:&&\mu\gt\$1.06\end{eqnarray*}[/latex]
    • [latex]p-\text{value}=0.0502[/latex]
    • Conclusion: At the [latex]1\%[/latex] significance level, there is not enough evidence to conclude that the mean cost of a daily newspaper has increased.

     

  4. In the past, the mean salary for managers at fast-food restaurants was [latex]\$68,500[/latex] with a standard deviation of [latex]\$9,200[/latex]. The manager at a local fast-food restaurant wants to test this claim because she believes the mean salary is higher now. In a sample of [latex]50[/latex] fast-food restaurant managers, the mean salary was [latex]\$70,600[/latex]. At the [latex]5\%[/latex] significance level, test the manager’s claim.
    Click to see Answer
    • Hypotheses: [latex]\begin{eqnarray*}H_0:&&\mu=\$68,500\\H_a:&&\mu\gt\$68,500\end{eqnarray*}[/latex]
    • [latex]p-\text{value}=0.0533[/latex]
    • Conclusion: At the [latex]5\%[/latex] significance level, there is not enough evidence to conclude that the mean salary for managers at fast-food restaurants has increased.

     

  5. A market research firm is studying consumer spending habits on Boxing Day. Based on previous research, the mean amount a consumer spends on Boxing Day is [latex]\$490[/latex] with a standard deviation of [latex]\$107[/latex]. Due to changes in the economy, consumer spending habits have also changed. In a sample of [latex]200[/latex] consumers, the mean amount spent on Boxing Day was [latex]\$510[/latex]. At the [latex]5\%[/latex] significance level, test the market research firm’s claim that the mean amount a consumer spends on Boxing Day has changed.
    Click to see Answer
    • Hypotheses: [latex]\begin{eqnarray*}H_0:&&\mu=\$490\\H_a:&&\mu\neq\$490\end{eqnarray*}[/latex]
    • [latex]p-\text{value}=0.0082[/latex]
    • Conclusion: At the [latex]5\%[/latex] significance level, there is enough evidence to conclude that the mean amount a consumer spends on Boxing Day has changed.

     

  6. A company claims that the mean time a customer waits on hold when calling the customer service support line is [latex]5[/latex] minutes with a standard deviation of [latex]1.36[/latex] minutes. The manager of the customer service call center believes that improvements made in training and protocols at the center have lowered the mean customer wait time. The manager takes a sample of [latex]70[/latex] days and records the wait times. The mean wait time in the sample is [latex]4.65[/latex]. At the [latex]5\%[/latex] significance level, test if the mean time a customer waits on hold is less than the company’s claim.
    Click to see Answer
    • Hypotheses: [latex]\begin{eqnarray*}H_0:&&\mu=5\text{ minutes}\\H_a:&&\mu\lt 5\text{ minutes}\end{eqnarray*}[/latex]
    • [latex]p-\text{value}=0.00157[/latex]
    • Conclusion: At the [latex]5\%[/latex] significance level, there is enough evidence to conclude that the mean time a customer waits on hold is less than [latex]5[/latex] minutes.

     

  7. Suppose that a recent article stated that the mean time spent in jail by a first-time convicted burglar is [latex]2.5[/latex] years. A study was then done to see if the mean time has increased in the new century. A random sample of [latex]26[/latex] first-time convicted burglars in a recent year was picked. The mean length of time in jail from the survey was [latex]3[/latex] years.  Suppose that it is somehow known that the population standard deviation is [latex]1.5[/latex]years. At the [latex]5\%[/latex] significance level, determine if the mean length of jail time has increased. Assume the distribution of the jail times is approximately normal.
    Click to see Answer
    • Hypotheses: [latex]\begin{eqnarray*}H_0:&&\mu=2.5\text{ years}\\H_a:&&\mu\gt 2.5\text{ years}\end{eqnarray*}[/latex]
    • [latex]p-\text{value}=0.0446[/latex]
    • Conclusion: At the [latex]5\%[/latex] significance level, there is enough evidence to conclude that the mean length of jail time has increased.

     

“8.6 Hypothesis Tests for a Population Mean with Known Population Standard Deviation” and “8.9 Exercises” from Introduction to Statistics by Valerie Watts is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Introduction to Statistics - Second Edition Copyright © 2025 by Valerie Watts is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.

Share This Book