"

5.2 The Normal Distribution

LEARNING OBJECTIVES

  • Describe properties of the normal distribution.
  • Apply the Empirical Rule for normal distributions.

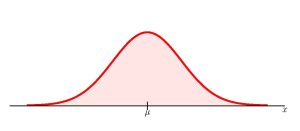
The normal distribution is the most important of all the distributions. It is widely used and even more widely abused. The normal distribution is a continuous probability distribution associated with a continuous random variable. The graph of a normal distribution is a symmetric, bell-shaped curve. This bell curve is used in almost all disciplines, including psychology, business, economics, the sciences, nursing, and, of course, mathematics. Most IQ scores are normally distributed. Often, real-estate prices fit a normal distribution. The normal distribution is extremely important, but it cannot be applied to everything in the real world.

This is a curve for a normal distribution. It shows a single peak in the center with the curve tapering down to the horizontal axis on each side. The distribution is symmetrical. It represents the random variable X having a normal distribution with a mean mu and standard deviation sigma. The distribution is centered at the mean mu.

Properties of the normal distribution include:

  • The curve of a normal distribution is symmetric and bell-shaped.
  • The center of a normal distribution is at the mean [latex]\mu[/latex].
  • In a normal distribution, the mean, the median, and the mode are equal.
  • The curve is symmetric about a vertical line drawn through the mean.
  • The tails of a normal distribution extend to infinity in both directions along the [latex]x[/latex]-axis.
  • The standard deviation, [latex]\sigma[/latex], of a normal distribution determines the shape, narrow or wide, of the curve.
  • The total area under the curve of a normal distribution equals [latex]1[/latex].

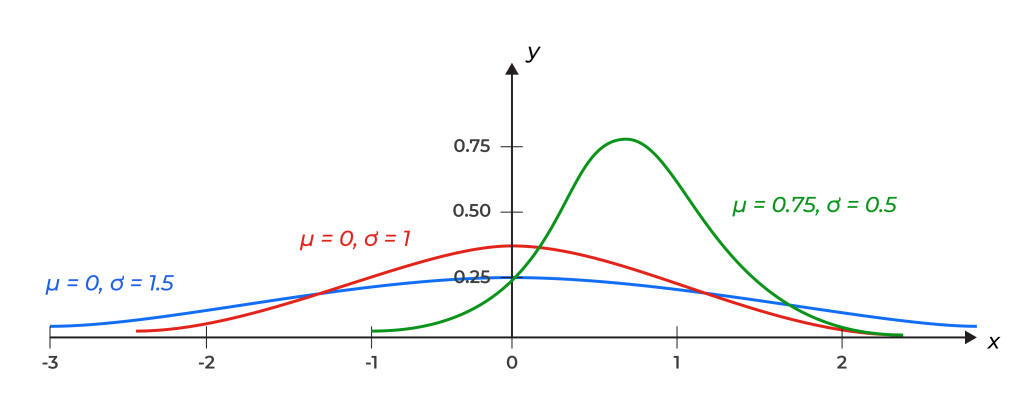
A normal distribution is completely determined by its mean [latex]\mu[/latex] and its standard deviation [latex]\sigma[/latex], which means there are an infinite number of normal distributions.  The mean [latex]\mu[/latex] determines the center of the distribution—a change in the value of [latex]\mu[/latex] causes the graph to shift to the left or right. The standard deviation [latex]\sigma[/latex] determines the shape, narrow or wide, of the bell. Because the area under the curve must equal one, a change in the standard deviation [latex]\sigma[/latex] causes a change in the shape of the curve—the curve becomes fatter or skinnier depending on the value of [latex]\sigma[/latex].

The image shows three different normal distribution curves. One curve has a mean of 0.75 and standard deviation of 0.5. Another graph has a mean of 0 and a standard deviation of 1. Another graph has a mean of 0 and a standard deviation of 1.5. The graphs are all symmetric and bell-shaped, but the shape of the bell is different because of the different standard deviations.

 

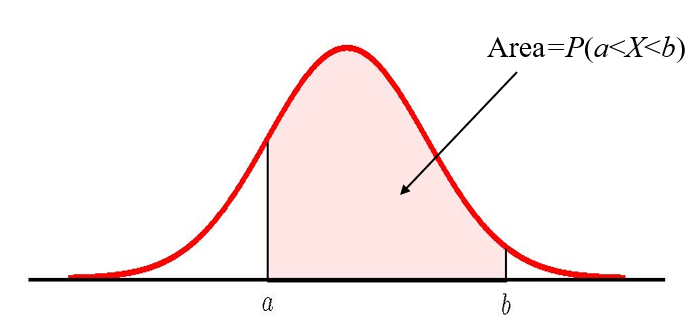
As we saw in the previous section, the area under the curve of the normal distribution equals the probability that the corresponding normal random variable takes on a value within a given interval. That is, the probability that the normal random variable is in between [latex]a[/latex] and [latex]b[/latex] equals the area under the normal curve in between [latex]x=a[/latex] and [latex]x=b[/latex].

This is a normal distribution. On the horizontal axis the points a and b are labeled. The area under the curve to the right of a and to the left of b is shaded. The shaded area is marked with an label reading Area equals probability x is in between a and b.

Video: “Continuous probability distribution intro” by Khan Academy [9:58] is licensed under the Standard YouTube License.Transcript and closed captions available on YouTube.

The Empirical Rule

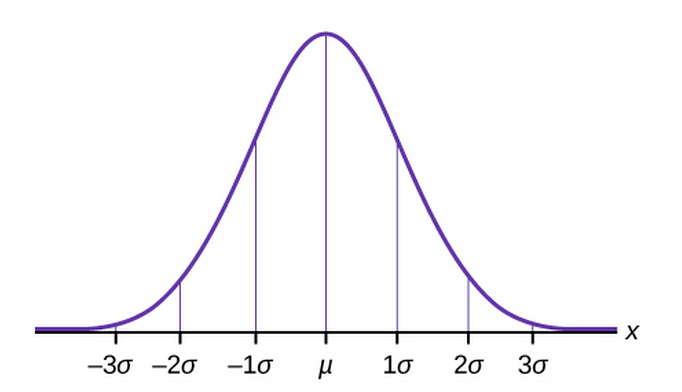
For a normal distribution with mean [latex]\mu[/latex] and standard deviation [latex]\sigma[/latex], the Empirical Rule says the following:

  • About [latex]68\%[/latex] of the values lie between [latex]–1 \times \sigma[/latex] and [latex]+1 \times \sigma[/latex] of the mean [latex]\mu[/latex].  In other words, about [latex]68\%[/latex] of the data fall with one standard deviation of the mean.
  • About [latex]95\%[/latex] of the values lie between [latex]–2 \times \sigma[/latex] and [latex]+2 \times \sigma[/latex] of the mean [latex]\mu[/latex].  In other words, about [latex]95\%[/latex] of the data fall with two standard deviation of the mean.
  • About [latex]99.7\%[/latex] of the values lie between [latex]–3 \times \sigma[/latex] and [latex]+3 \times \sigma[/latex] of the mean [latex]\mu[/latex].  In other words, about [latex]99.7\%[/latex] of the data fall with three standard deviation of the mean

The empirical rule is also known as the [latex]68-95-99.7[/latex] rule.

Graph of the empirical Rule

EXAMPLE

Suppose a normal distribution has a mean of [latex]50[/latex] and a standard deviation of [latex]6[/latex].

The Empirical Rule says:

  • About [latex]68\%[/latex] of the values lie between [latex]–1 \times \sigma = -1 \times 6 = –6[/latex] and [latex]1 \times \sigma = 1 \times 6 = 6[/latex] of the mean [latex]50[/latex].  The values [latex]50 – 6 = 44[/latex] and [latex]50 + 6 = 56[/latex] are within one standard deviation of the mean [latex]50[/latex]. So [latex]68\%[/latex] of the values in this distribution are between [latex]44[/latex] and [latex]56[/latex].
  • About [latex]95\%[/latex] of the values lie between [latex]–2 \times \sigma = -2 \times 6 = –12[/latex] and [latex]2 \times \sigma = 2 \times 6 = 12[/latex] of the mean [latex]50[/latex].  The values [latex]50 – 12 = 38[/latex] and [latex]50 + 12 = 62[/latex] are within two standard deviations of the mean [latex]50[/latex]. So [latex]95\%[/latex] of the values in the distribution are between [latex]38[/latex] and [latex]62[/latex].
  • About [latex]99.7\%[/latex] of the values lie between [latex]–3 \times \sigma = -3 \times 6 = –18[/latex] and [latex]3 \times \sigma = 3 \times 6 = 18[/latex] of the mean [latex]50[/latex].  The values [latex]50 – 18 = 32[/latex] and [latex]50 + 18= 68[/latex] are within three standard deviations of the mean [latex]50[/latex]. So [latex]99.7\%[/latex] of the values in the distribution are between [latex]32[/latex] and [latex]68[/latex].

TRY IT

Suppose a normal distribution has a mean of [latex]25[/latex] and a standard deviation of [latex]5[/latex]. [latex]68\%[/latex] of the values lie between what two numbers?

 

Click to see Solution

 

Between [latex]25+(-1) \times 5=20[/latex] and [latex]25+1 \times 5=30[/latex].

EXAMPLE

From 1984 to 1985, the height of 15 to 18-year-old males from Chile follows a normal distribution with mean [latex]172.36[/latex]cm and standard deviation [latex]6.34[/latex]cm.

  1. About [latex]68\%[/latex] of the heights of 15 to 18-year-old males in Chile from 1984 to 1985 lie between what two values?
  2. About [latex]95\%[/latex] of the heights of 15 to 18-year-old males in Chile from 1984 to 1985 lie between what two values?
  3. About [latex]99.7\%[/latex] of the heights of 15 to 18-year-old males in Chile from 1984 to 1985 lie between what two values?

Solution

  1. [latex]\displaystyle{\mu+(-1)\times \sigma=172.36+(-1)\times 6.34=166.02}[/latex] and [latex]\displaystyle{\mu+1 \times \sigma=172.36+1 \times 6.34=178.70}[/latex]
  2. [latex]\displaystyle{\mu+(-2)\times \sigma=172.36+(-2)\times 6.34=159.68}[/latex] and [latex]\displaystyle{\mu+2 \times \sigma=172.36+2 \times 6.34=185.04}[/latex]
  3. [latex]\displaystyle{\mu+(-3)\times \sigma=172.36+(-1)\times 6.34=153.34}[/latex] and [latex]\displaystyle{\mu+3 \times \sigma=172.36+2 \times 6.34=191.36}[/latex]

TRY IT

The scores on a college entrance exam have an approximate normal distribution with a mean of [latex]52[/latex] points and a standard deviation of [latex]11[/latex] points.

  1. About [latex]68\%[/latex] of the exam scores lie between what two values?
  2. About [latex]95\%[/latex] of the exam scores lie between what two values?
  3. About [latex]99.7\%[/latex] of the exam scores lie between what two values?
Click to see Solution
  1. About [latex]68\%[/latex] of the scores lie between the values [latex]52+(-1) \times 11=41[/latex] and [latex]52+1 \times 11=63[/latex].
  2. About [latex]95\%[/latex] of the values lie between the values [latex]52+(-2) \times 11=30[/latex] and [latex]52+2 \times 11=74[/latex].
  3. About [latex]99.7\%[/latex] of the values lie between the values [latex]52+(-3) \times 11=19[/latex] and [latex]52+3 \times 11=85[/latex].

Video: “ck12.org normal distribution problems: Empirical rule | Probability and Statistics | Khan Academy” by Khan Academy [10:25] is licensed under the Standard YouTube License.Transcript and closed captions available on YouTube.

Exercises

  1. A normal distribution has a mean of [latex]61[/latex] and a standard deviation of [latex]15[/latex]. What is the median?
    Click to see Answer

    [latex]61[/latex]

     

  2. About what percent of the values of a normal distribution lie within one standard deviation (left and right) of the mean of that distribution?
    Click to see Answer

    [latex]68\%[/latex]

     

  3. About what percent of the values of a normal distribution lie within two standard deviations (left and right) of the mean of that distribution?
    Click to see Answer

    [latex]95\%[/latex]

     

  4. About what percent of the values of a normal distribution lie between the second and third standard deviations (both sides)?
    Click to see Answer

    [latex]4.7\%[/latex]

     

  5. Suppose [latex]X[/latex] is a normal random variable with mean [latex]15[/latex] and standard deviation [latex]3[/latex]. Between what two values does [latex]68\%[/latex] of the data lie?
    Click to see Answer

    [latex]15[/latex] and [latex]18[/latex]

     

  6. Suppose [latex]X[/latex] is a normal random variable with mean [latex]-3[/latex] and standard deviation [latex]1[/latex].
    1. Between what two values does [latex]95\%[/latex] of the data lie?
    2. Between what two values does [latex]34\%[/latex] of the data lie?
    Click to see Answer
    1. [latex]-5[/latex] and [latex]-1[/latex]
    2. [latex]-4[/latex] and [latex]-3[/latex] or [latex]-3[/latex] and [latex]-2[/latex]

     

  7. About what percent of the values of a normal distribution lie between the mean and three standard deviations?
    Click to see Answer

    [latex]49.85\%[/latex]

     

  8. About what percent of the values of a normal distribution lie between the mean and one standard deviation?
    Click to see Answer

    [latex]34\%[/latex]

     

  9. About what percent of the values of a normal distribution lie between the first and second standard deviations from the mean (both sides)?
    Click to see Answer

    [latex]27\%[/latex]

     

  10. About what percent of the values of a normal distribution lie between the first and third standard deviations (both sides)?
    Click to see Answer

    [latex]31.7\%[/latex]

     

  11. The salaries of employees of a large technology company follow a normal distribution with a mean of [latex]\$65,000[/latex] and a standard deviation of [latex]\$1,700[/latex].
    1. [latex]68\%[/latex] of the salaries lie between what two values?
    2. [latex]99.7\%[/latex] of the salaries lie between what two values?
    3. [latex]2.5\%[/latex] of the salaries lie above what value?
    4. [latex]16\%[/latex] of the salaries lie below what value?
    5. [latex]97\%[/latex] of the salaries lie above what value?
    6. What percentage of salaries lie between [latex]\$61,600[/latex] and [latex]\$68,400[/latex]?
    7. What percentage of salaries lie above [latex]\$70,100[/latex]?
    8. What percentage of salaries lie below [latex]\$61,600[/latex]?
    9. What percentage of salaries lie between [latex]\$65,000[/latex] and [latex]\$68,400[/latex]?
    10. What percentage of salaries lie above [latex]\$66,700[/latex]?
    Click to see Answer
    1. [latex]\$63,300[/latex] and [latex]\$66,700[/latex]
    2. [latex]\$59,900[/latex] and [latex]\$70,100[/latex]
    3. [latex]\$68,400[/latex]
    4. [latex]\$63,300[/latex]
    5. [latex]\$61,600[/latex]
    6. [latex]95\%[/latex]
    7. [latex]0.15\%[/latex]
    8. [latex]2.5\%[/latex]
    9. [latex]47.5\%[/latex]
    10. [latex]16\%[/latex]

     

  12. A factory produces light bulbs. The lifespan of the light bulbs follows a normal distribution with a mean of [latex]1200[/latex] hours and a standard deviation of [latex]100[/latex] hours.
    1. [latex]95\%[/latex] of the bulbs have lifespans between what two values?
    2. [latex]16\%[/latex] of the bulbs have lifespans above what value?
    3. [latex]0.15\%[/latex] of the bulbs have lifespans below what value?
    4. [latex]99.85\%[/latex] of the bulbs have lifespans below what value?
    5. [latex]84\%[/latex] of the bulbs have lifespans above what value?
    6. What percentage of bulbs have lifespans between [latex]1100[/latex] hours and [latex]1300[/latex] hours?
    7. What percentage of bulbs have lifespans below [latex]1000[/latex] hours?
    8. What percentage of bulbs have lifespans above [latex]1500[/latex] hours?
    9. What percentage of bulbs have lifespans below [latex]1400[/latex] hours?
    10. What percentage of bulbs have lifespans between [latex]900[/latex] hours and [latex]1200[/latex] hours?
    11. What percentage of bulbs have lifespans between [latex]1200[/latex] hours and [latex]1300[/latex] hours?
    Click to see Answer
    1. [latex]1000[/latex] hours and [latex]1400[/latex] hours
    2. [latex]1300[/latex] hours
    3. [latex]900[/latex] hours
    4. [latex]1500[/latex] hours
    5. [latex]1100[/latex] hours
    6. [latex]68\%[/latex]
    7. [latex]2.5\%[/latex]
    8. [latex]0.15\%[/latex]
    9. [latex]97.55\%[/latex]
    10. [latex]49.85\%[/latex]
    11. [latex]34\%[/latex]

     

  13. The distribution of the heights of adult women follows a normal distribution with a mean of [latex]163[/latex] cm and a standard deviation of [latex]8[/latex] cm.
    1. [latex]99.7\%[/latex] of women have heights between what two values?
    2. [latex]84\%[/latex] of women have heights above what value?
    3. [latex]0.15\%[/latex] of women have heights above what value?
    4. [latex]97.5\%[/latex] of women have heights below what value?
    5. What percentage of women have heights between [latex]155[/latex] cm and [latex]171[/latex] cm?
    6. What percentage of women have heights below [latex]139[/latex] cm?
    7. What percentage of women have heights above [latex]171[/latex] cm?
    8. What percentage of women have heights above [latex]147[/latex] cm?
    9. What percentage of women have heights between [latex]147[/latex] cm and [latex]163[/latex] cm?
    Click to see Answer
    1. [latex]139[/latex] cm and [latex]187[/latex] cm
    2. [latex]155[/latex] cm
    3. [latex]187[/latex] cm
    4. [latex]179[/latex] cm
    5. [latex]68\%[/latex]
    6. [latex]0.15\%[/latex]
    7. [latex]16\%[/latex]
    8. [latex]97.5\%[/latex]
    9. [latex]47.5\%[/latex]

     

“5.3 The Normal Distribution” and “5.6 Exercises” from Introduction to Statistics by Valerie Watts is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Introduction to Statistics - Second Edition Copyright © 2025 by Valerie Watts is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.

Share This Book