9 Factoriser

Quelques identités remarquables

$\begin{eqnarray*}&& a^2 - b^2 = (a+ b) (a-b) \\ \\&& a^2 + 2 a b + b^2 = (a+b)^2 \\ \\ && a^2 - 2 a b + b^2 = (a-b)^2 \\ \\ && a^3 + b^3 = (a+b) (a^2 - ab + b^2)\\ \\ && a^3 - b^3 = (a-b) (a^2 + ab + b^2) \end{eqnarray*}$

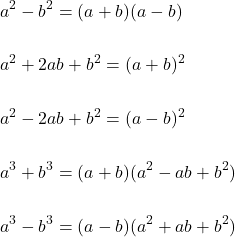
Comment factoriser un polynôme?

– identifier un facteur commun

– factoriser en regroupant les termes communs

– utiliser les identités remarquables.

Voir la Vidéo

Voir sur YouTube

Afficher les Exemples

Exercice 1

Afficher/Masquer Solution.

$5(x^2+ 4)^4 (2x) (x-2)^4 + (x^2+ 4)^5 (4) (x-2)^3$

$= (x^2+ 4)^4 (x-2)^3 \Big[ 5(2x) (x-2) + (x^2+4) (4)\Big]$

$= (x^2+ 4)^4 (x-2)^3 \Big[ 14x^2 -20 x +16\Big]$ .

Exercice 2

Afficher/Masquer Solution.

Posons $t= x^2 + 1$ . On a

$(x^2 +1)^2 - 7 (x^2 + 1) + 10 = t^2 - 7 t +10 = (t - 2) (t-5)$

$= [ x^2 + 1- 2] [ x^2 +1 - 5 ] = (x^2 - 1) (x^2 -4)$

$= (x- 1) (x+1)( x - 2)(x+2)$

On a utilisé l’identité : $a^2 - b^2 = (a-b) (a+b)$ .

Exercice 3

Afficher/Masquer Solution.

On factorise l’expression en regroupant les termes.

$x^5 + x^4 + x + 1 = x^4( x+ 1) + x + 1 = (x+1) ( x^4 + 1 )$

$x^9 + x^8 + 2x^5 + 2x^4 + x + 1$
$= x^8( x+ 1) + 2x^4( x+ 1) + x + 1$
$=(x+1) (x^8 +2 x^4 + 1 )$
$=(x+1) ( x^4 + 1 )^2$

Donc, le facteur commun est : $(x+1) ( x^4 + 1 )^2$ .

Exercice 4

Afficher/Masquer Solution.

On applique l’identité : $a^3 + b^3 = (a + b) (a^2 - a b + b^2 )$ .

$x^3 +{27} = x^3 +(3)^3 = (x+{3}) (x^2 - {3} x + {3}^2 ).$

Exercice 5

Afficher/Masquer Solution.

On utilise la méthode de complétion d’un carré parfait. On a

$16 z^2 - 24 z + 9 = (4z)^2 - 2 (4 z) (3) + (3)^2 = (4z-3)^2$

On a utilisé l’identité : $a^2 -2 a b + b^2 = (a-b)^2$ .

Pour $8 z^2 + 2 z - 6$ , on peut utiliser la méthode précédente ou la méthode du déterminant.

On a $\Delta = (2)^2- 4(8)(-6)= 4. (49)$ et les racines sont

$z_1= (-2-14)/16 =-1, \qquad \qquad z_2 = (-2+14)/16=3/4$

Donc $8 z^2 + 2 z - 6 = 8(z+1) (z-3/4)= 2(z+1)(4z-3).$

Par conséquent, le facteur commun est : $(4z-3)$ .

Licence

Symbole de Licence Creative Commons Attribution - Pas d’utilisation commerciale - Pas de modification 4.0 International

Guide de Révision du Pré-calcul Droit d'auteur © 2025 par Samia CHALLAL est sous licence Licence Creative Commons Attribution - Pas d’utilisation commerciale - Pas de modification 4.0 International, sauf indication contraire.

Partagez ce livre