11 Exposants rationnels
* Pour ![]() , la racine
, la racine ![]() -ième principale de
-ième principale de ![]() , est définie par :
, est définie par :
![]()
![]() si
si ![]() est impair
est impair
![]()
![]()
![]() si
si ![]() est pair
est pair
![Rendered by QuickLaTeX.com \[ \qquad \left\|\begin{matrix} y= x^{1/n} \qquad & \hbox{ si } \quad x > 0 \qquad & \hbox{ avec }\quad y= x^{1/n}\quad \Longleftrightarrow \quad x=y^n \\ \\ 0\qquad & \hbox{ si } \quad x=0 & \\ \\ \hbox{ indéfini}\qquad &\hbox{ si}\quad x < 0 \qquad & \end{matrix}\right. \]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-759762a8fda85111f8a295f0d7202ff0_l3.png)
![]()
![]()
![Rendered by QuickLaTeX.com \[ \quad \Big(x^n\Big)^{1/n} = \left\{\begin{matrix} x \qquad & \hbox{ si } \quad n \quad \hbox{ est impair } \\ \\ |x|\qquad & \hbox{ si } \quad n \quad\hbox{ est pair } \end{matrix}\right. \]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-c7719df70ba1ea8a94cf0281135db99c_l3.png)
Exercice 1
Afficher/Masquer Solution.
En utilisant les lois des exposants, on a
![]()
Exercice 2
Afficher/Masquer Solution.
En utilisant les lois des exposants, on a
![]()
Exercice 3
Afficher/Masquer Solution.
En utilisant les lois des exposants, on a
![]()
=![]()
=![]()
= ![]()
Exercice 4
Afficher/Masquer Solution.
En utilisant les lois des exposants, on a
![]()
=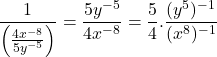
= ![]() =
= ![]() =
= ![]()
Exercice 5
Afficher/Masquer Solution.
En utilisant les lois des exposants, on a
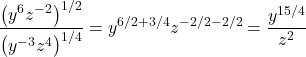
Exercice 6
Afficher/Masquer Solution.
En utilisant les lois des exposants, on a
![]()
![]() .
. ![]() .
.![]()
![]() .
. ![]() .
.![]() =
= ![]()

