6.8 Work, Energy, and Power in Humans
Learning Objectives
By the end of this section, you will be able to:
- Explain the human body’s consumption of energy when at rest vs. when engaged in activities that do useful work.
- Calculate the conversion of chemical energy in food into useful work.
Energy Conversion in Humans
Our own bodies, like all living organisms, are energy conversion machines. Conservation of energy implies that the chemical energy stored in food is converted into work, thermal energy, and/or stored as chemical energy in fatty tissue. (See Figure 6.23.) The fraction going into each form depends both on how much we eat and on our level of physical activity. If we eat more than is needed to do work and stay warm, the remainder goes into body fat.
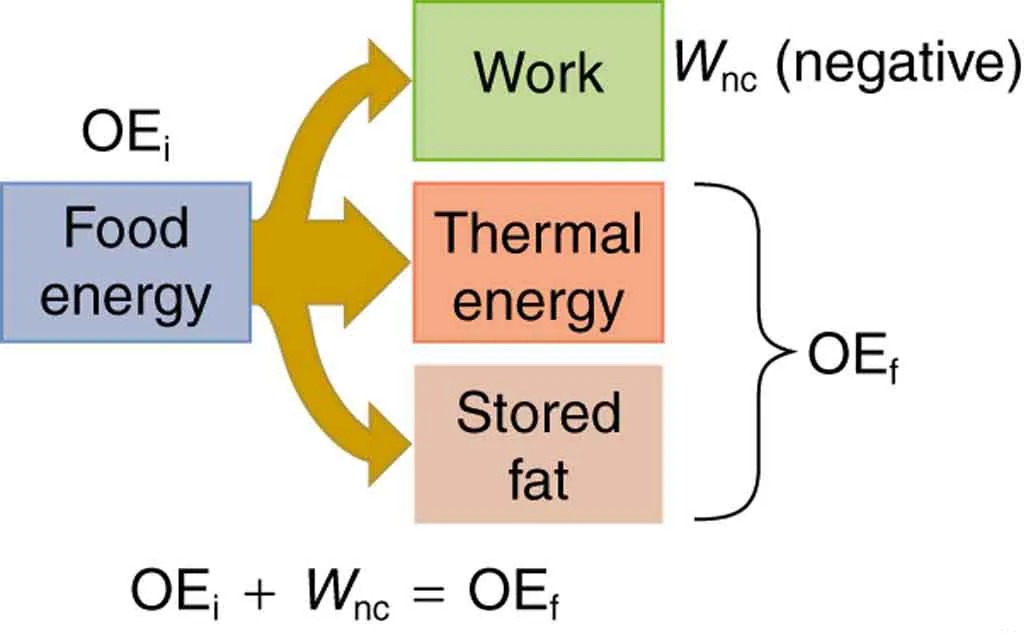
Figure 6.23 Energy consumed by humans is converted to work, thermal energy, and stored fat. By far the largest fraction goes to thermal energy, although the fraction varies depending on the type of physical activity. Image from OpenStax College Physics 2e, CC-BY 4.0
Image Description
The image is a diagram illustrating the flow and conversion of food energy.
– On the left side, there is a blue rectangle labeled “OEi Food energy.”
– Arrows from this rectangle divide the energy into three categories on the right:
– A green rectangle labeled “Work” with a notation “Wnc (negative)”
– An orange rectangle labeled “Thermal energy”
– A red rectangle labeled “Stored fat”
– To the right of the rectangles, the diagram groups “Thermal energy” and “Stored fat” under “OEf“.
– At the bottom, there is an equation: “OEi + Wnc = OEf“.
This diagram represents the concept of energy balance, showing how food energy is allocated to work, heat, and fat storage.
Power Consumed at Rest
The rate at which the body uses food energy to sustain life and to do different activities is called the metabolic rate. The total energy conversion rate of a person at rest is called the basal metabolic rate (BMR) and is divided among various systems in the body, as shown in Table 6.4. The largest fraction goes to the liver and spleen, with the brain coming next. Of course, during vigorous exercise, the energy consumption of the skeletal muscles and heart increase markedly. About 75% of the calories burned in a day go into these basic functions. The BMR is a function of age, gender, total body weight, and amount of muscle mass (which burns more calories than body fat). Athletes have a greater BMR due to this last factor.
| Organ | Power consumed at rest (W) | Oxygen consumption (mL/min) | Percent of BMR |
|---|---|---|---|
| Liver & spleen | 23 | 67 | 27 |
| Brain | 16 | 47 | 19 |
| Skeletal muscle | 15 | 45 | 18 |
| Kidney | 9 | 26 | 10 |
| Heart | 6 | 17 | 7 |
| Other | 16 | 48 | 19 |
| Totals | 85 W | 250 mL/min | 100% |
Power of Doing Useful Work
Work done by a person is sometimes called useful work, which is work done on the outside world, such as lifting weights. Useful work requires a force exerted through a distance on the outside world, and so it excludes internal work, such as that done by the heart when pumping blood. Useful work does include that done in climbing stairs or accelerating to a full run, because these are accomplished by exerting forces on the outside world. Forces exerted by the body are nonconservative, so that they can change the mechanical energy ([latex]\text{KE } + \text{ PE}[/latex]) of the system worked upon, and this is often the goal. A baseball player throwing a ball, for example, increases both the ball’s kinetic and potential energy.
If a person needs more energy than they consume, such as when doing vigorous work, the body must draw upon the chemical energy stored in fat. So exercise can be helpful in losing fat. However, the amount of exercise needed to produce a loss in fat, or to burn off extra calories consumed that day, can be large, as Example 6.13 illustrates.
Example 6.13
Calculating Weight Loss from Exercising
If a person who normally requires an average of 12,000 kJ (3000 kcal) of food energy per day consumes 13,000 kJ per day, they will steadily add body fat. How much bicycling per day is required to work off this extra 1000 kJ?
Solution
Table 6.5 states that 400 W are used when cycling at a moderate speed. The time required to work off 1000 kJ at this rate is then
[latex]\text{Time} = \frac{\text{energy}}{\left(\frac{\text{energy}}{\text{time}}\right)} = \frac{\text{1000 kJ}}{\text{400 W}} = \text{2500 s} = \text{42 min}.[/latex]
Discussion
If this person uses more energy than they consume, the person’s body will obtain the needed energy by metabolizing body fat. If the person uses 13,000 kJ but consumes only 12,000 kJ, then the amount of fat loss will be
[latex]\text{Fat loss} = \left(\right. \text{1000 kJ} \left.\right) \left(\frac{\text{1}.\text{0 g fat}}{\text{39 kJ}}\right) = \text{26} \text{ g},[/latex]
assuming the energy content of fat to be 39 kJ/g.
| Activity | Energy consumption in watts | Oxygen consumption in liters O2/min |
|---|---|---|
| Sleeping | 83 | 0.24 |
| Sitting at rest | 120 | 0.34 |
| Standing relaxed | 125 | 0.36 |
| Sitting in class | 210 | 0.60 |
| Walking (5 km/h) | 280 | 0.80 |
| Cycling (13–18 km/h) | 400 | 1.14 |
| Shivering | 425 | 1.21 |
| Playing tennis | 440 | 1.26 |
| Swimming breaststroke | 475 | 1.36 |
| Ice skating (14.5 km/h) | 545 | 1.56 |
| Climbing stairs (116/min) | 685 | 1.96 |
| Cycling (21 km/h) | 700 | 2.00 |
| Running cross-country | 740 | 2.12 |
| Playing basketball | 800 | 2.28 |
| Cycling, professional racer | 1855 | 5.30 |
| Sprinting | 2415 | 6.90 |
- for a 76-kg male with typical metabolic functions ↵

