16.4 Introduction to pH and pOH

Learning Objectives

By the end of this section, you will be able to:
  • Explain the characterization of aqueous solutions as acidic, basic, or neutral
  • Express hydronium and hydroxide ion concentrations on the pH and pOH scales
  • Perform calculations relating pH and pOH

As discussed earlier, hydronium and hydroxide ions are present both in pure water and in all aqueous solutions, and their concentrations are inversely proportional as determined by the ion product of water (Kw). The concentrations of these ions in a solution are often critical determinants of the solution’s properties and the chemical behaviours of its other solutes, and specific vocabulary has been developed to describe these concentrations in relative terms. A solution is neutral if it contains equal concentrations of hydronium and hydroxide ions; acidic if it contains a greater concentration of hydronium ions than hydroxide ions; and basic if it contains a lesser concentration of hydronium ions than hydroxide ions. To assist with informing users of a substance’s acidity or basicity (alkalinity), one can calculate the pH of the substance and reference it on the pH scale. For a brief introduction into the pH scale and how it is used, Watch The pH Scale Explained (5min 54s).

Video Source: Chem Academy. (2015, April 28). The pH scale explained. [Video]. YouTube.

Introduction to the pH Scale

The pH scale is a scale of acidity ranging 0 to 14 (but not always). It indicates how acidic or basic a solution is. You can use pH to make a quick determination whether a given aqueous solution is acidic, basic, or neutral. Since the pH of a substance is dependent on hydronium ion concentration, [H3O+], the following conclusions (at standard temperature of 25 °C) can be inferred:

  • If pH < 7, then the solution is acidic.
  • If pH = 7, then the solution is neutral.
  • If pH > 7, then the solution is basic.
Most substances have a pH in the range of 0 to 14, although extremely acidic or alkaline substances may have pH < 0, or pH > 14, respectively.
Source: “pH” by Simple English Wikipedia, licensed under CC BY-SA 3.0. 

Exercise 16.4a

Check Your Learning Exercise (Text Version)

Label each solution as acidic, basic, or neutral based only on the given pH value:

  1. Household bleach, pH = 12.6
  2. Lime Juice, pH = 2.3
  3. Milk of Magnesia, pH = 10.5
  4. Pure Water, pH = 7
  5. Vinegar, pH = 2.5
  6. Baking soda, pH = 8.5

Check Your Answer[1]

Source: “Exercise 16.4a” by Jackie MacDonald, licensed under CC BY-NC-SA 4.0.

Formulas for Calculating pH, pOH, [H3O+] and [OH–]

A common means of expressing quantities, the values of which may span many orders of magnitude, is to use a logarithmic scale. One such scale that is very popular for chemical concentrations and equilibrium constants is based on the p-function, defined as shown where “X” is the quantity of interest and “log” is the base-10 logarithm:

[latex]\text{pX} = -\text{log X}[/latex]

The pH of a solution is therefore defined as shown here, where [H3O+] is the molar concentration of hydronium ion in the solution:

[latex]\text{pH} = -\text{log[H}_3\text{O}^{+}][/latex]

Rearranging this equation to isolate the hydronium ion molarity yields the equivalent expression:

[latex][\text{H}_3\text{O}^{+}] = 10^{-\text{pH}}[/latex]

Likewise, the hydroxide ion molarity may be expressed as a p-function, or pOH:

[latex]\text{pOH} = -\text{log[OH}^{-}][/latex]

or

[latex][\text{OH}^{-}] = 10^{-\text{pOH}}[/latex]

Finally, the relation between these two ion concentration expressed as p-functions is easily derived from the Kw expression:

Kw = [H3O+][OH–]

-log Kw = -log([H3O+][OH–]) = -log[H3O+]+ -log[OH–]

pKw = pH + pOH

At 25 °C, the value of Kw is 1.0 × 10−14, and so:

14.00 = pH + pOH

As was shown in Example 16.3a in Chapter 16.3 Ionization of Water, Brønsted-Lowry Acids and Bases, the hydronium ion molarity in pure water (or any neutral solution) is 1.0 × 10−7M at 25 °C. The pH and pOH of a neutral solution at this temperature are therefore:

[latex]\text{pH} = -\text{log[H}_3\text{O}^{+}] = -\text{log}(1.0\;\times\;10^{-7}) = 7.00[/latex]
[latex]\text{pOH} = -\text{log[OH}^{-}] = -\text{log}(1.0\;\times\;10^{-7}) = 7.00[/latex]

And so, at this temperature, acidic solutions are those with hydronium ion molarities greater than 1.0 × 10−7M and hydroxide ion molarities less than 1.0 × 10−7M (corresponding to pH values less than 7.00 and pOH values greater than 7.00). Basic solutions are those with hydronium ion molarities less than 1.0 × 10−7M and hydroxide ion molarities greater than 1.0 × 10−7M (corresponding to pH values greater than 7.00 and pOH values less than 7.00).

Since the autoionization constant Kw is temperature dependent, these correlations between pH values and the acidic/neutral/basic adjectives will be different at temperatures other than 25 °C. For example, the hydronium molarity of pure water at 80 °C is 4.9 × 10−7M, which corresponds to pH and pOH values of:

[latex]\text{pH} = -\text{log[H}_3\text{O}^{+}] = -\text{log}(4.9\;\times\;10^{-7}) = 6.31[/latex]
[latex]\text{pOH} = -\text{log[OH}^{-}] = -\text{log}(4.9\;\times\;10^{-7}) = 6.31[/latex]

At this temperature, then, neutral solutions exhibit pH = pOH = 6.31, acidic solutions exhibit pH less than 6.31 and pOH greater than 6.31, whereas basic solutions exhibit pH greater than 6.31 and pOH less than 6.31. This distinction can be important when studying certain processes that occur at nonstandard temperatures, such as enzyme reactions in warm-blooded organisms. Unless otherwise noted, references to pH values are presumed to be those at standard temperature (25 °C) (Table 16.4a).

Table 16.4a Summarizing pH Properties for Acidic, Basic and Neutral Solutions
Classification Relative Ion Concentrations pH at 25 °C
acidic [H3O+] > [OH−] pH < 7
neutral [H3O+] = [OH−] pH = 7
basic [H3O+] < [OH−] pH > 7

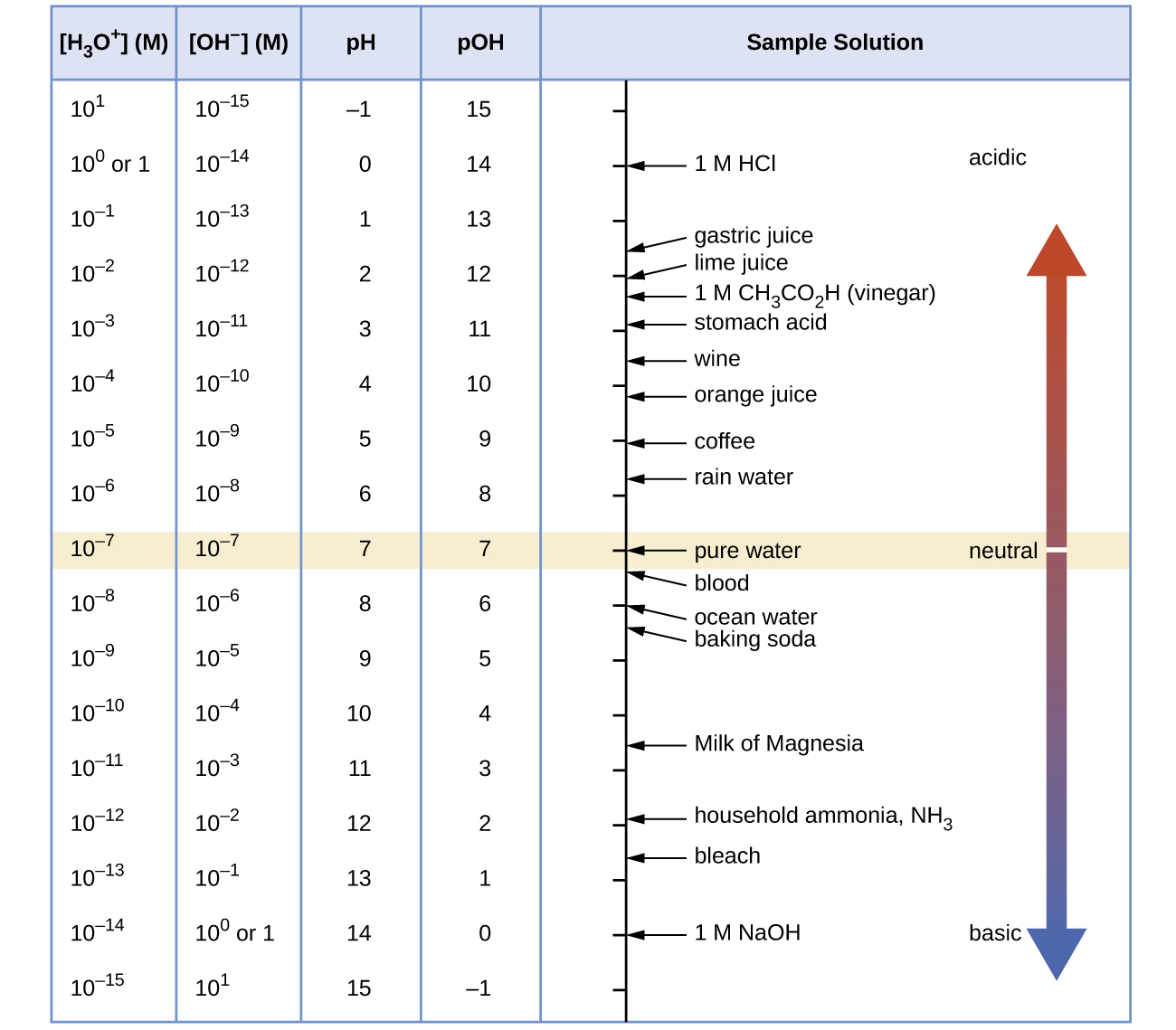
Figure 16.4a shows the relationships between [H3O+], [OH−], pH, and pOH, and gives values for these properties at standard temperatures for some common substances.

A table is provided with 5 columns. The first column is labeled “left bracket H subscript 3 O superscript plus right bracket (M).” Powers of ten are listed in the column beginning at 10 superscript 1, including 10 superscript 0 or 1, 10 superscript negative 1, decreasing by single powers of 10 to 10 superscript negative 15. The second column is labeled “left bracket O H superscript negative right bracket (M).” Powers of ten are listed in the column beginning at 10 superscript negative 15, increasing by single powers of 10 to including 10 superscript 0 or 1, and 10 superscript 1. The third column is labeled “p H.” Values listed in this column are integers beginning at negative 1, increasing by ones up to 14. The fourth column is labeled “p O H.” Values in this column are integers beginning at 15, decreasing by ones up to negative 1. The fifth column is labeled “Sample Solution.” A vertical line at the left of the column has tick marks corresponding to each p H level in the table. Substances are listed next to this line segment with line segments connecting them to the line to show approximate p H and p O H values. 1 M H C l is listed at a p H of 0. Gastric juices are listed at a p H of about 1.5. Lime juice is listed at a p H of about 2, followed by 1 M C H subscript 3 C O subscript 2 H, followed by stomach acid at a p H value of nearly 3. Wine is listed around 3.5. Coffee is listed just past 5. Pure water is listed at a p H of 7. Pure blood is just beyond 7. Milk of Magnesia is listed just past a p H of 10.5. Household ammonia is listed just before a pH of 12. 1 M N a O H is listed at a p H of 0. To the right of this labeled arrow is an arrow that points up and down through the height of the column. A beige strip passes through the table and to this double headed arrow at p H 7. To the left of the double headed arrow in this beige strip is the label “neutral.” A narrow beige strip runs through the arrow. Just above and below this region, the arrow is purple. It gradually turns to a bright red as it extends upward. At the top of the arrow, near the head of the arrow is the label “acidic.” Similarly, the lower region changes color from purple to blue moving to the bottom of the column. The head at this end of the arrow is labeled “basic.”
Figure 16.4a Relationships between [H3O+], [OH−], pH, and pOH: The pH and pOH scales represent concentrations of [H3O+] and OH−, respectively. The pH and pOH values of some common substances at standard temperature (25 °C) are shown in this chart (credit: Chemistry (OpenStax), CC BY 4.0).

Determining pH and pOH from its Reciprocal pH/pOH Value

pOH scale is fairly similar to pH, except instead of measuring the hydrogen ion concentration in moles per litre, it measures the hydroxide ion concentration in moles per litre.  As shown earlier in this section (during standard temperature conditions), pH and pOH must add up to 14:

14.00 = pH + pOH

So if you are given pH, you can determine pOH by rearranging the formula:

pOH = 14 – pH

Alternatively, if you are given pOH, you can determine pH by rearranging the formula:

pH = 14 – pOH

Example 16.4a

A cleaning solution has a pOH of 2.5. Calculate the pH of this solution and determine whether this solution is acidic, basic, or neutral.

Solution

Given information

pOH = 2.5

To find the pH, use the formula

pH = 14 – pOH

Solve:

pH = 14 – 2.5

pH = 11.5; this cleaning solution is basic since its pH is greater than 7.

Exercise 16.4b

Exercise 16.4b Part 1:

For each solution listed below, calculate its pOH and determine whether this solution is acidic, basic, or neutral.

  1. Solution that has a pH = 9.25
  2. Solution that has a pH = 3.8

Exercise 16.4b Part 2:

For each solution listed below, calculate its pH and determine whether this solution is acidic, basic, or neutral.

  1. Solution that has a pOH = 5.65
  2. Solution that has a pOH = 13.1

Check Your Answer[2]

Essentially, the scale for pOH is the reverse of the pH scale.

Source: “Determining pH and pOH from its Reciprocal pH/pOH Value” by Jackie MacDonald, CC-BY-NC-SA 4.0

The acidity of a solution is typically assessed experimentally by measurement of its pH. The pOH of a solution is not usually measured, as it is easily calculated from an experimentally determined pH value. The pH of a solution can be directly measured using a pH meter (Figure 16.4c).

The first image is of an analytical digital p H meter on a laboratory counter. The second image is of a portable handheld digital p H meter.
Figure 16.4b (a) A research-grade pH meter used in a laboratory can have a resolution of 0.001 pH units, an accuracy of ± 0.002 pH units, and may cost in excess of 1000 dollars. (b) A portable pH meter has lower resolution (0.01 pH units), lower accuracy (± 0.2 pH units), and a far lower price tag. (credit a: work by Datamax, PD; credit b: modification of work by Laurence Livermore, CC BY 2.0)

The pH of a solution may also be visually estimated using coloured indicators (Figure 16.4d).

This figure contains two images. The first shows a variety of colors of solutions in labeled beakers. A red solution in a beaker is labeled “0.10 M H C l.” An orange solution is labeled “0.10 M C H subscript 3 C O O H.” A yellow-orange solution is labeled “0.1 M N H subscript 4 C l.” A yellow solution is labeled “deionized water.” A second solution beaker is labeled “0.10 M K C l.” A green solution is labeled “0.10 M aniline.” A blue solution is labeled “0.10 M N H subscript 4 C l (a q).” A final beaker containing a dark blue solution is labeled “0.10 M N a O H.” Image b shows pHydrion paper that is used for measuring pH in the range of p H from 1 to 12. The color scale for identifying p H based on color is shown along with several of the test strips used to evaluate p H.
Figure 16.4c (a) A universal indicator assumes a different colour in solutions of different pH values. Thus, it can be added to a solution to determine the pH of the solution. The eight vials each contain a universal indicator and 0.1-M solutions of progressively weaker acids: HCl (pH = l), CH3CO2H (pH = 3), and NH4Cl (pH = 5), deionized water, a neutral substance (pH = 7); and 0.1-M solutions of the progressively stronger bases: KCl (pH = 7), aniline, C6H5NH2 (pH = 9), NH3 (pH = 11), and NaOH (pH = 13). (b) pH paper contains a mixture of indicators that give different colours in solutions of differing pH values. (credit: modification of work by Sahar Atwa in Chemistry (OpenStax), CC BY 4.0).

Calculating pH when given Hydronium Concentration

When you are given a solution’s hydronium concentration, its pH can be calculated using the formula: [latex]\text{pH} = -\text{log[H}_3\text{O}^{+}][/latex]

Example 16.4b

Calculation of pH from [H3O+]
What is the pH of stomach acid, a solution of HCl with a hydronium ion concentration of 1.2 × 10−3M?

Solution

[latex]\begin{array}{r @{{}={}} l}\text{pH} & = -\text{log[H}_3\text{O}^{+}]\\[0.5em] & = -\text{log}(1.2\;\times\;10^{-3})\\[0.5em] & = -(-2.92)\\[0.5em] & = 2.92\end{array}[/latex]

(The use of logarithms is explained in Appendix B – The Use of Logarithms and Exponential Numbers Section).

Recall that, as we have done here, when taking the log of a value, keep as many decimal places in the result as there are significant figures in the value.). To review significant figures for logarithm calculations, Watch Significant Figures and Logarithms (2min 0s).

Video Source: Study Force (2019, July 22). Significant figures and logarithms [Video]. YouTube.

Exercise 16.4c

Water exposed to air contains carbonic acid, H2CO3, due to the reaction between carbon dioxide and water:

[latex]\text{CO}_2(aq)\; \text{+}\;\text{H}_2\text{O}(l)\;{\leftrightharpoons}\;\text{H}_2\text{CO}_3(aq)[/latex]

Air-saturated water has a hydronium ion concentration caused by the dissolved CO2 of 2.0 × 10−6M, about 20-times larger than that of pure water. Calculate the pH of the solution at 25 °C.

Check Your Answer[3]

Calculating Hydronium Concentration when given the pH

When you are given a solution’s pH, its hydronium concentration can be calculated using the formula: [latex][\text{H}_3\text{O}^{+}] = 10^{-\text{pH}}[/latex]

Example 16.4c

Calculation of Hydronium Ion Concentration from pH
Calculate the hydronium ion concentration of blood that has a pH of 7.3 (slightly alkaline).

Solution

Use the formula:

[latex][\text{H}_3\text{O}^{+}] = 10^{-\text{pH}}[/latex]

Solve given that the pH = 7.3

[H3O+] = 10-7.3

[H3O+] = 5 x 10-8 M

Therefore, the hydronium ion concentration of blood with a pH of 7.3 is 5 x 10-8 M

Source: “Example 16.4c” by Jackie MacDonald, CC-BY-NC-SA 4.0

Exercise 16.4d

Calculate the hydronium ion concentration of a solution with a pH of −1.07.

Check Your Answer[4]

Source: “Exercise 16.4d” by Jackie MacDonald, CC-BY-NC-SA 4.0

Calculating pOH when given Hydroxide Concentration

When you are given a solution’s hydronium concentration, its pH can be calculated using the formula: [latex]\text{pOH} = -\text{log[OH}^{-}][/latex]

Example 16.4d

What are the pOH and the pH of a 0.0125 M solution of potassium hydroxide, KOH?

Solution

Potassium hydroxide is a highly soluble ionic compound and completely dissociates when dissolved in dilute solution, yielding [OH−] = 0.0125 M:

[latex]\begin{array}{r @{{}={}} l}\text{pOH} & = -\text{log[OH}^{-}]\\[0.5em] & = -\text{log}(0.0125) \\[0.5em] & = -(-1.903)\\[0.5em] & = 1.903\end{array}[/latex]

The pH can be found from the pOH:

[latex]\begin{array}{r @{{}={}} l}\text{pH}\;+\;\text{pOH} & = 14.00 \\[0.5em] \text{pH} & = 14.00\;-\;\text{pOH}\\[0.5em] & = 14.00\;-\;1.903\\[0.5em] & = 12.10\end{array}[/latex]

 

Exercise 16.4e

The hydroxide concentration of a sodium hydroxide solution is 0.091 M. Determine the pOH and pH of the solution.

Check Your Answer[5]

Calculating Hydroxide Concentration when given the pOH

When you are given a solution’s hydronium concentration, its pH can be calculated using the formula: [latex][\text{OH}^{-}] = 10^{-\text{pOH}}[/latex]

Example 16.4e

Calculation of [OH–]

The pOH of house hold bleach is 1.45. What is the [OH–] of this solution?

Solution

Use the formula [OH–] = 10-pOH to determine the hydroxide concentration of the bleach solution.

[OH–] = 10-pOH

[OH–] = 10-1.45

[OH–] = 0.035 M or 3.5 x 10-2 M

Source: “Example 16.4e” by Jackie MacDonald, CC-BY-NC-SA 4.0

Exercise 16.4f

The pOH of toilet a bowl cleaner is measured to be 12.35. What is the [OH–] of this solution? Is this solution acidic or basic?

Check Your Answer[6]

Source: “Exercise 16.5f” by Jackie MacDonald, CC-BY-NC-SA 4.0

Acid/Base Calculations involving Two Steps

Figure 16.4b below shows all of the calculation interrelationships between [H3O+], [OH−], pH, and pOH. The flow chart can be referenced to support students in determining which formula(s) need to be used to solve a given problem.

This flow chart diagram illustrates the various calculations/interrelationships between [H3O+], [OH−], pH, and pOH. 1. To find pH when given pOH use: pH = 14 - pOH. 2. To find pOH when given pH use: pOH = 14 - pH 3. To find pH when given [H3O+] use: pH = -log[H3O+] 4. To find pOH when given [OH-] use: pOH = -log[OH-] 5. To find [H3O+] when given pH use: [H3O+] = 10^-pH. 6. To find [OH-] when given pOH use: [OH-] = 10^-pOH. 7. To find [H3O+] when given [OH-] use: [H3O+] = 1.0x10^-14 / [OH-] 8. To find [OH-] when given [H3O+] use: [OH-] = 1.0x10^-14 / [H3O+]
Figure 16.4d Calculation Relationships between Hydrogen Ion Concentration, Hydroxide Concentration, pH and pOH: Use the flow chart to determine which formula(s) to use to answer an acid/base calculation. To begin, locate the unit of the given information on the diagram that was provided in the question. Next, locate the unit of the answer you are asked to calculate. Use the formula(s) to solve the question that is associated with the arrow(s) pointing in the direction of the unit you are trying to calculate. It may be a one step or two step problem. (credit: Figure 16.4b by Jackie MacDonald, CC-BY-NC-SA 4.0).

Example 16.4f

Acidic soils typically yield blue or lavender-blue hydrangea blooms. Alkaline (basic) soil tends to grow pinkish-red blooms. If soil has a [OH–] of 6.3 x 10-7 M, what is pH of the soil and what colour blooms will this soil promote for hydrangeas growing in this soil?

Solution:

Given information: [OH–] = 6.3 x 10-7 M

Asked to find: the pH of soil and, thus, the likely colour of the flower’s blooms

Steps – First find pOH, then calculate pH. If acidic, blooms will be blue; if alkaline, blooms will be pink/red.

Step 1 – Calculate pOH using pOH = -log[OH–]

pOH = -log[6.3 x 10-7]

pOH = 6.20

Step 2 – Find the pH and determine colour of the blooms

pH = 14 – pOH

pH = 14 – 6.20

pH = 7.80

Therefore the pH of the soil is 7.80, which is slightly alkaline, so the blooms will be a pinkish/red colour.

Source: “Example 16.4e” by Jackie MacDonald, CC BY-NC-SA 4.0

Exercise 16.4g

The hydronium ion concentration of vinegar is approximately 4 × 10−3M. What is the pOH of this solution?

Check Your Answer[7]

Source: “Exercise 16.4g” by Jackie MacDonald, CC-BY-NC-SA 4.0

Links to Interactive Learning Tools

Explore pH and pOH from the Physics Classroom.

Attribution & References

Except where otherwise noted, this page is adapted by Jackie MacDonald from:

  1. (1) Basic; (2) Acidic; (3) Basic; (4) Neutral; (5) Acidic; (6) Basic ↵
  2. Part 1 (a) pOH = 4.75, basic; (b) pOH = 10.2, acidic; Part 2 (a) pH = 8.35, basic; (b) pH = 0.9, acidic ↵
  3. pH = 5.70 ↵
  4. [H3O+] = 12 M ↵
  5. Step 1: Find pOH using [latex]\text{pOH} = -\text{log[OH}^{-}][/latex]; therefore, pOH = 1.04; pH = 14 - 1.04 = 12.96 ↵
  6. Use the formula [OH-] = 10-pOH to determine the hydroxide concentration of the bleach solution. [OH-] = 10-pOH [OH-] = 10-12.35 [OH-] = 4.5 x 10-13 M; since the pOH is higher than 7, this means its corresponding pH is below 7, and the solution is acidic. ↵
  7. Step 1: Find pH first using pH = -log[H3O+]; pH = 2.4; Step 2 calculate pOH: pOH = 14 - pH = 14 - 2.4 = 11.6 ↵
definition

License

Icon for the Creative Commons Attribution 4.0 International License

Chemistry v. 1 backup Copyright © 2023 by Gregory Anderson; Caryn Fahey; Jackie MacDonald; Adrienne Richards; Samantha Sullivan Sauer; J.R. van Haarlem; and David Wegman is licensed under a Creative Commons Attribution 4.0 International License, except where otherwise noted.

Share This Book